湘教版八年级下册2.4 三角形的中位线(第1课时) 课件(共15张PPT)
文档属性
| 名称 | 湘教版八年级下册2.4 三角形的中位线(第1课时) 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
本课内容
本节内容
2.4
第1课时
湘教版数学 八年级下册
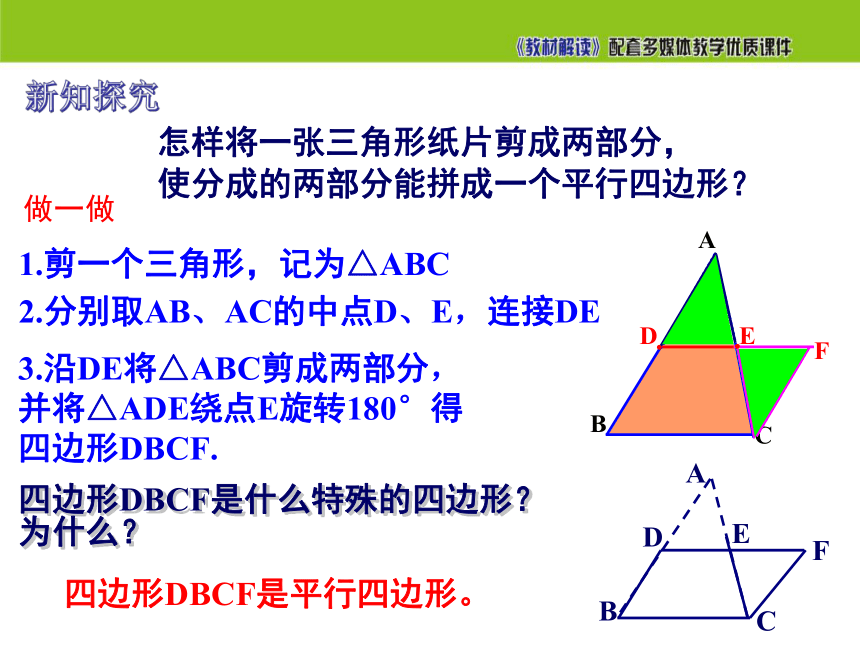
怎样将一张三角形纸片剪成两部分,
使分成的两部分能拼成一个平行四边形?
1.剪一个三角形,记为△ABC
2.分别取AB、AC的中点D、E,连接DE
3.沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180°得四边形DBCF.
A
B
C
F
D
·
E
·
四边形DBCF是什么特殊的四边形?为什么?
做一做
A
B
C
D
E
F
四边形DBCF是平行四边形。
连接三角形两边的中点的线段叫做三角形的中位线。
图中线段DE 是连接△ABC两边的中点D、E所得的线段,称此线段DE为△ABC的中位线。
E
D
C
B
A
思考:1.三角形有几条中位线?
2.三角形中位线与中线有什么区别?
A
B
C
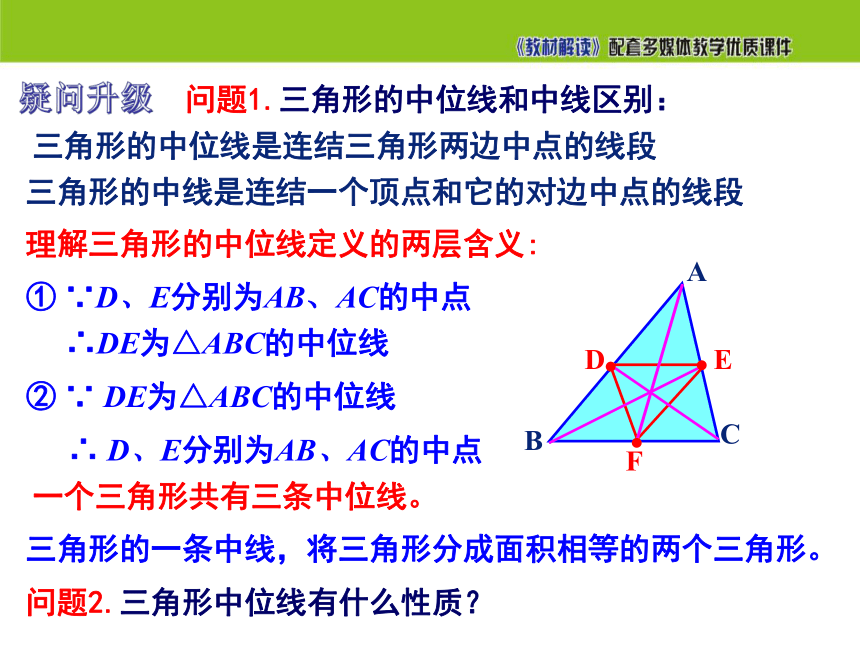
三角形的中位线是连结三角形两边中点的线段
三角形的中线是连结一个顶点和它的对边中点的线段
问题1.三角形的中位线和中线区别:
理解三角形的中位线定义的两层含义:
② ∵ DE为△ABC的中位线
① ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
一个三角形共有三条中位线。
D
E
F
三角形的一条中线,将三角形分成面积相等的两个三角形。
问题2.三角形中位线有什么性质?
三角形的中位线有什么性质?
如图,EF是△ABC的一条中位线.
数量关系:量一量,EF,BC的长
各是多少?你有什么猜想?
G
三角形中位线平行第三边,且等于第三边的一半。
位置关系:你能从图中猜想
EF∥BC 吗?
数量关系?位置关系?
我猜测EF∥BC, EF= BC.
2
1
这些猜想正确吗?
我们来证明:
如图,将△AEF绕点F旋转180°,
至△CGF的位置。
设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E, F,G在一条直线上.
由旋转不变性得:
CG=AE=BE,GF=EF,∠G=∠AEF.
则 AE∥CG. (内错角相等,两直线平行)
即 BE∥CG.
又 BE=CG,
所以四边形BEGC是平行四边形.(一组对边平行且相等的四边形是平行四边形)
所以EG=BC,EG∥BC.
(平行四边形的对边平行且相等)
又因为EF=GF,
所以 EF = EG = BC,EF∥BC.
1
2
1
2
结论:
三角形的中位线平行于第三边,
并且等于第三边的一半
几何表示:
∵EF是△ ABC的中位线
∴EF= BC,EF∥BC.
2
1
解:连结AC.
由于EF是△ABC的一条中位线,
由于MH是△ DAC的一条中位线,
于是EF∥MH,且EF=MH.
所以四边形EFHM是平行四边形.
例1 如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?
顺次连结四边形各边中点得到的四边形是平行四边形。
因此MH∥AC,且MH= AC
2
1
因此EF∥AC,且EF= AC.
2
1
∵点E、F分别是OB、OC的中点,EF是 OBC的中位线。
例2 .□ABCD的对角线相交于点O.点 E、F、P分别为OB、OC、AD的中点,且AC=2AB.求证:EP=EF.
证明:连接AE,
∴AD=BC,AC=2OA=2OC. ∵AC=2AB,∴OA=AB.
∵E为OB中点,∴AE⊥BD ∴∠AED=90°.
即: AED是直角三角形。
1
2
∴EF= BC. ∴EP=EF.
A
B
C
D
O
E
F
P
∵P为AD中点 ∴EP= AD.
2
1
∵ BC=AD,∴ EP= BC.
1
2
∵四边形ABCD是平行四边形,
1.如图1:在△ABC中,DE是中位线
(1)若∠CDE=60°,则∠B= ,
(2)若BC=8cm,则DE= cm,
60°
4
图1
A
B
C
D
E
2.如图2:在△ABC中,D、E、F分别是各边中点AB=6cm,AC=8cm,BC=10cm,则△DEF的周长= cm
图2
B
A
C
D
E
F
12
26
做完2、3题后,你有何体会 ?
3.已知三角形的3条中位线分别是3,4,6 则这个三角形的周长是 。
4.如图3,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中
点,N 是边AB 的中点,则△MPN
是 三角形?
等腰
(为什么?)
D
C
B
A
P
N
M
图3
5.已知: 如图,DE,EF是 ABC的两条中位线.
求证:四边形BFED是平行四边形.
D
B
C
F
E
A
MP=NP= AD
1
2
DE∥BF,
DE= BC=BF.
1
2
6.如图,△ABC的边BC,CA,AB的中点分别是D,E,F.
(1)四边形AFDE是平行四边形吗?
为什么?
可证:DE=AF,DF=AE.
∴四边形AFDE是平行四边形.
(2)四边形AFDE的周长等于AB+AC吗?
为什么?
=AB+AC
DE+AF+DE+AE= AB+ AB+ AC+ AC
2
1
2
1
2
1
2
1
7.如图,在△ABC中,点D在BC上,且CD=AC,CE⊥AD垂足为E,点F是AB的中点。求证:EF∥BC
E
A
B
C
D
F
如果已知AC=10,BC=14,求EF的长。
8.已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边△ABM和等边△CAN,D,E,F分别是MB,BC,CN的中点,连结DE,FE,
求证:DE=FE
A
N
M
F
E
D
C
B
证得△ABN≌△ACM,
从而得MC=BN,再证得DE=FE。
提示:连接MC,BN
由条件得:点E是AD的中点。EF是
△ABD的中位线,结论得证。
EF=2
为了测量这个池塘的宽AB,在池塘一侧的平地上选一点C,再分别找出线段AC,BC的中点D、E,若测出DE的长,就能求出池塘AB的长,你知道为什么吗?
A
B
D
E
C
仅给一把有刻度的卷尺,能否测出一个池塘的宽AB?(注意﹕不能直接测量)
DE是△ABC的中位线。
AB=2DE
本节课学习了三角形的中位线的概念及其性质.
定义 连结三角形两边中点的线段叫做三角形的中位线.
性质:三角形的中位线平行于第三边,并且等于第三边的一半.
2、若题中含有中点或隐含中点的条件时,常构造三角形中位线解决问题。
1、利用三角形的中位线是证明线段的平行和倍分问题的方法之一。
3、在解决四边形的有关问题时,常常连接对角线把四边形转化为三角形解决。
利用性质解决问题:
作业:p57 A 1、2、3
本课内容
本节内容
2.4
第1课时
湘教版数学 八年级下册
怎样将一张三角形纸片剪成两部分,
使分成的两部分能拼成一个平行四边形?
1.剪一个三角形,记为△ABC
2.分别取AB、AC的中点D、E,连接DE
3.沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180°得四边形DBCF.
A
B
C
F
D
·
E
·
四边形DBCF是什么特殊的四边形?为什么?
做一做
A
B
C
D
E
F
四边形DBCF是平行四边形。
连接三角形两边的中点的线段叫做三角形的中位线。
图中线段DE 是连接△ABC两边的中点D、E所得的线段,称此线段DE为△ABC的中位线。
E
D
C
B
A
思考:1.三角形有几条中位线?
2.三角形中位线与中线有什么区别?
A
B
C
三角形的中位线是连结三角形两边中点的线段
三角形的中线是连结一个顶点和它的对边中点的线段
问题1.三角形的中位线和中线区别:
理解三角形的中位线定义的两层含义:
② ∵ DE为△ABC的中位线
① ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
一个三角形共有三条中位线。
D
E
F
三角形的一条中线,将三角形分成面积相等的两个三角形。
问题2.三角形中位线有什么性质?
三角形的中位线有什么性质?
如图,EF是△ABC的一条中位线.
数量关系:量一量,EF,BC的长
各是多少?你有什么猜想?
G
三角形中位线平行第三边,且等于第三边的一半。
位置关系:你能从图中猜想
EF∥BC 吗?
数量关系?位置关系?
我猜测EF∥BC, EF= BC.
2
1
这些猜想正确吗?
我们来证明:
如图,将△AEF绕点F旋转180°,
至△CGF的位置。
设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E, F,G在一条直线上.
由旋转不变性得:
CG=AE=BE,GF=EF,∠G=∠AEF.
则 AE∥CG. (内错角相等,两直线平行)
即 BE∥CG.
又 BE=CG,
所以四边形BEGC是平行四边形.(一组对边平行且相等的四边形是平行四边形)
所以EG=BC,EG∥BC.
(平行四边形的对边平行且相等)
又因为EF=GF,
所以 EF = EG = BC,EF∥BC.
1
2
1
2
结论:
三角形的中位线平行于第三边,
并且等于第三边的一半
几何表示:
∵EF是△ ABC的中位线
∴EF= BC,EF∥BC.
2
1
解:连结AC.
由于EF是△ABC的一条中位线,
由于MH是△ DAC的一条中位线,
于是EF∥MH,且EF=MH.
所以四边形EFHM是平行四边形.
例1 如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?
顺次连结四边形各边中点得到的四边形是平行四边形。
因此MH∥AC,且MH= AC
2
1
因此EF∥AC,且EF= AC.
2
1
∵点E、F分别是OB、OC的中点,EF是 OBC的中位线。
例2 .□ABCD的对角线相交于点O.点 E、F、P分别为OB、OC、AD的中点,且AC=2AB.求证:EP=EF.
证明:连接AE,
∴AD=BC,AC=2OA=2OC. ∵AC=2AB,∴OA=AB.
∵E为OB中点,∴AE⊥BD ∴∠AED=90°.
即: AED是直角三角形。
1
2
∴EF= BC. ∴EP=EF.
A
B
C
D
O
E
F
P
∵P为AD中点 ∴EP= AD.
2
1
∵ BC=AD,∴ EP= BC.
1
2
∵四边形ABCD是平行四边形,
1.如图1:在△ABC中,DE是中位线
(1)若∠CDE=60°,则∠B= ,
(2)若BC=8cm,则DE= cm,
60°
4
图1
A
B
C
D
E
2.如图2:在△ABC中,D、E、F分别是各边中点AB=6cm,AC=8cm,BC=10cm,则△DEF的周长= cm
图2
B
A
C
D
E
F
12
26
做完2、3题后,你有何体会 ?
3.已知三角形的3条中位线分别是3,4,6 则这个三角形的周长是 。
4.如图3,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中
点,N 是边AB 的中点,则△MPN
是 三角形?
等腰
(为什么?)
D
C
B
A
P
N
M
图3
5.已知: 如图,DE,EF是 ABC的两条中位线.
求证:四边形BFED是平行四边形.
D
B
C
F
E
A
MP=NP= AD
1
2
DE∥BF,
DE= BC=BF.
1
2
6.如图,△ABC的边BC,CA,AB的中点分别是D,E,F.
(1)四边形AFDE是平行四边形吗?
为什么?
可证:DE=AF,DF=AE.
∴四边形AFDE是平行四边形.
(2)四边形AFDE的周长等于AB+AC吗?
为什么?
=AB+AC
DE+AF+DE+AE= AB+ AB+ AC+ AC
2
1
2
1
2
1
2
1
7.如图,在△ABC中,点D在BC上,且CD=AC,CE⊥AD垂足为E,点F是AB的中点。求证:EF∥BC
E
A
B
C
D
F
如果已知AC=10,BC=14,求EF的长。
8.已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边△ABM和等边△CAN,D,E,F分别是MB,BC,CN的中点,连结DE,FE,
求证:DE=FE
A
N
M
F
E
D
C
B
证得△ABN≌△ACM,
从而得MC=BN,再证得DE=FE。
提示:连接MC,BN
由条件得:点E是AD的中点。EF是
△ABD的中位线,结论得证。
EF=2
为了测量这个池塘的宽AB,在池塘一侧的平地上选一点C,再分别找出线段AC,BC的中点D、E,若测出DE的长,就能求出池塘AB的长,你知道为什么吗?
A
B
D
E
C
仅给一把有刻度的卷尺,能否测出一个池塘的宽AB?(注意﹕不能直接测量)
DE是△ABC的中位线。
AB=2DE
本节课学习了三角形的中位线的概念及其性质.
定义 连结三角形两边中点的线段叫做三角形的中位线.
性质:三角形的中位线平行于第三边,并且等于第三边的一半.
2、若题中含有中点或隐含中点的条件时,常构造三角形中位线解决问题。
1、利用三角形的中位线是证明线段的平行和倍分问题的方法之一。
3、在解决四边形的有关问题时,常常连接对角线把四边形转化为三角形解决。
利用性质解决问题:
作业:p57 A 1、2、3
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
