湘教版八年级下册2.4 三角形的中位线 (第2课时 )课件(共13张PPT)
文档属性
| 名称 | 湘教版八年级下册2.4 三角形的中位线 (第2课时 )课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 917.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 12:58:49 | ||
图片预览


文档简介
(共13张PPT)
本课内容
本节内容
2.4
第2课时
湘教版数学 八年级下册
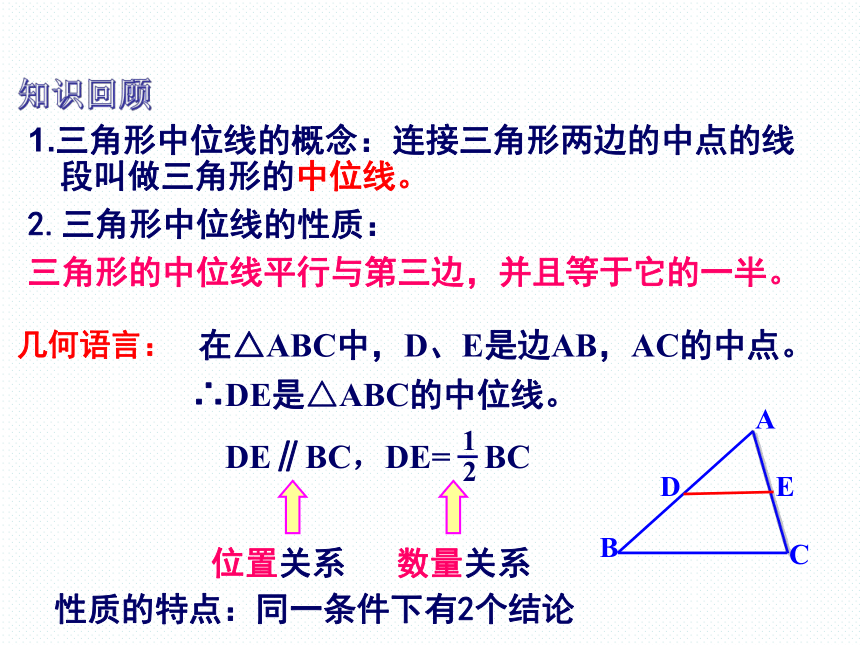
1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:
三角形的中位线平行与第三边,并且等于它的一半。
E
D
C
B
A
几何语言:
在△ABC中,D、E是边AB,AC的中点。
DE∥BC,DE= BC
1
2
∴DE是△ABC的中位线。
性质的特点:同一条件下有2个结论
位置关系 数量关系
上节课我们是通过旋转证明三角形中位线性质,还有其它证明方法吗?
证法二:如图,延长EF到G,使FG=EF,连接CG
在△ABC中,E、F是边ABAC的中点。
求证:EF∥BC,EF= BC
1
2
可证得:△AEF≌△CGF
∠EAF=∠GCF
CG∥AB
CG=AE=EB
∴四边形EBCG是平行四边形。
EF∥BC
且EF= EG= BC
1
2
1
2
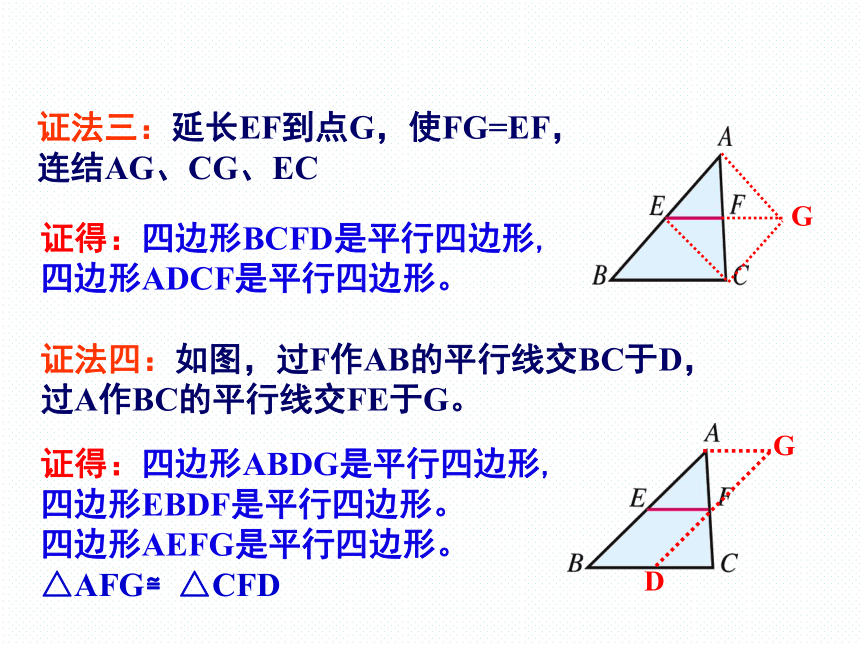
证法四:如图,过F作AB的平行线交BC于D,
过A作BC的平行线交FE于G。
G
D
证法三:延长EF到点G,使FG=EF,
连结AG、CG、EC
证得:四边形BCFD是平行四边形,
四边形ADCF是平行四边形。
G
证得:四边形ABDG是平行四边形,
四边形EBDF是平行四边形。
四边形AEFG是平行四边形。 △AFG≌△CFD
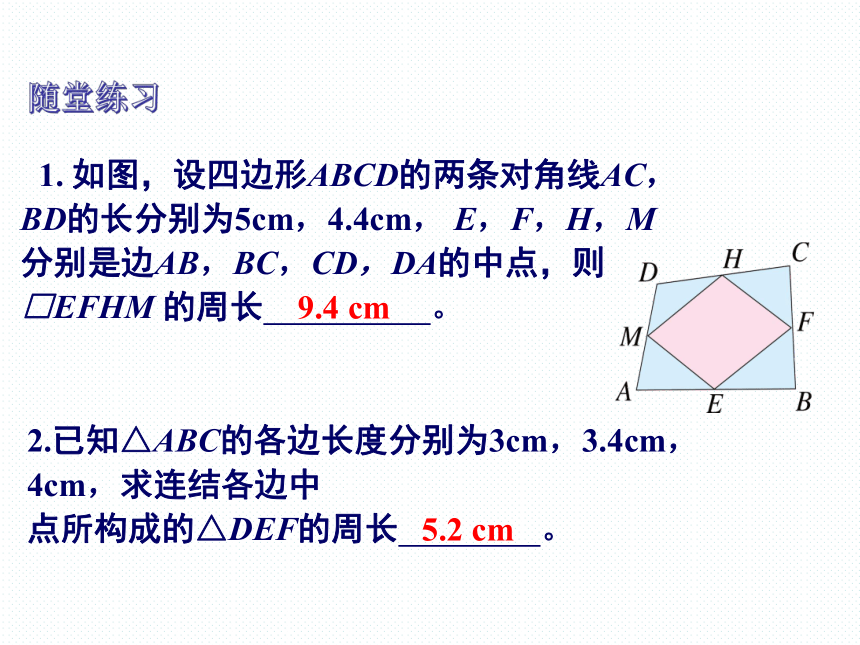
1. 如图,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm, E,F,H,M分别是边AB,BC,CD,DA的中点,则□EFHM 的周长 。
9.4 cm
2.已知△ABC的各边长度分别为3cm,3.4cm,4cm,求连结各边中
点所构成的△DEF的周长 。
5.2 cm
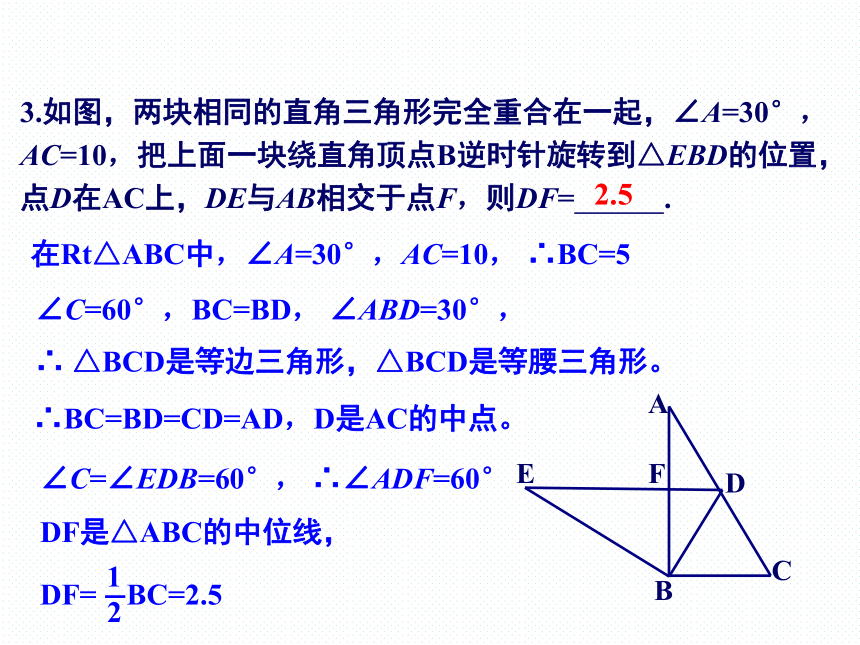
3.如图,两块相同的直角三角形完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△EBD的位置,点D在AC上,DE与AB相交于点F,则DF= .
2.5
A
B
C
D
E
F
在Rt△ABC中,∠A=30°,AC=10,
∴BC=5
∠C=60°,BC=BD, ∠ABD=30°,
∴ △BCD是等边三角形,△BCD是等腰三角形。
∴BC=BD=CD=AD,D是AC的中点。
∠C=∠EDB=60°, ∴∠ADF=60°
DF是△ABC的中位线,
DF= BC=2.5
1
2
例1 如图,□ABCD的周长为36.对角线AC,BD相交于点O.点E是CD的中点.BO=6.求△DOE的周长。
【解题思路】根据平行四边形的性质,对角线互相平分,两组对边分别相等,可以分别求出OD、OE+DE的长,即可求解.
∴△DOE的周长=OD+OE+DE=6+9=15
A
B
C
D
E
O
解:∵□ABCD的周长为36, ∴BC+CD=18,
∵四边形ABCD为平行四边形,
∴O是BD的中点, ∴OD=6,
又∵E是CD的中点,∴OE是△BCD的中位线,
∴OE+DE=9,
例2.求证:三角形的一条中位线与第三边上的中线互相平分.
已知,如图,△ABC中,D、E、F分别
是边AB、BC、CA的中点,DF、AE交
于点O,求证:DF与AE互相平分。
E
F
D
C
B
A
O
分析:根据“平行四边形对角线互相平分”的性质,只要能证明四边形ADEF是平行四边形即可。
又∵ DE、AE分别□ADEF的对角线。
∴ DF与AE互相平分。
证明:连接DE、EF
∵D、EF分别是AB、BC、AC中点
∴ DE∥AF,FE∥AD
∴ 四边形ADEF是平行四边形。
G
.
F
E
D
C
B
A
【解题思路】由条件,努力构造三角形中位线。取FC的中点G,连接DG。
这样F、G分别是AG、CF的中点。
例3.如图,AD是△ABC中线,E是AD的中点,BE交AC于F,AF= AC,试说明EF= BF
1
3
1
4
证明:取FC的中点G,连接DG
∵ AF= AC,
1
3
∴F、G是AC的三等分点。
又∵E是AD的中点,∴ EF= DG,
1
2
又∵D是BC的中点,∴ DG= BF,
1
2
1
4
∴ EF= DG= × BF= BF
1
2
1
2
1
2
A
B
C
D
E
F
1.已知: D、E、F分别为△ABC的边AB、AC、BC的中点。
(1)、已知DE=5,DF=4,EF=6,
则BC= ,AC= , AB= ,
△ DEF的周长= ,
△ ABC的周长= ,
△ ABC的周长是△DEF 周长的 ,
10
8
12
15
30
2倍
(2)、图中有 个平行四边形。
3
2.已知,如图,在△ABC中,AE=EC,AD⊥BC,EF⊥BC,BE=2EF,问AD与BE相等吗?为什么?
A
E
D
C
B
F
(3)连结AF,则AF是△ABC的 ,AF与DE 的关系是 。
(4)若△ABC的面积是 20,
则△DEF的面积是 ,
△DEF的面积是△ABC的面积的 。
中线
互相平分
5
1
4
结论:(1)三角形三条中位线围成的三角形周长是原
三角形周长的一半,面积是原三角形面积的四分之一。
(2)三角形的一条中位线与第三边上的中线互相平分。
A
B
C
D
E
F
AD=BE=2EF
3.已知:如图,AD是△ABC的高,M、N和E分别为AB、AC、BC的中点。
求证:EM=DN
N
M
E
D
C
B
A
提示:ME是△ABC的中位线,ME= AC.
1
2
N是Rt△ADC斜边AC的中点,DN是中线,DN= AC.
1
2
E
D
A
C
B
.
4.如图,在△ABC中,∠A=2∠B,CD⊥AB,E为AB的中点。求证:DE= AC
1
2
·
F
取BC的中点F,连接EF、DF
EF是△ABC的中位线,EF= AC,
1
2
∠A=∠FEB =2∠B,
∠FDE =∠B,
∠FDE =∠DFE,DE=EF
作业:p57 B 4、5、6
1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:
三角形的中位线平行与第三边,
并且等于它的一半。
E
D
C
B
A
3.应用三角形中位线的性质解决有关计算或
说理等问题时,根据条件,努力构造三角形中位线。
本课内容
本节内容
2.4
第2课时
湘教版数学 八年级下册
1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:
三角形的中位线平行与第三边,并且等于它的一半。
E
D
C
B
A
几何语言:
在△ABC中,D、E是边AB,AC的中点。
DE∥BC,DE= BC
1
2
∴DE是△ABC的中位线。
性质的特点:同一条件下有2个结论
位置关系 数量关系
上节课我们是通过旋转证明三角形中位线性质,还有其它证明方法吗?
证法二:如图,延长EF到G,使FG=EF,连接CG
在△ABC中,E、F是边ABAC的中点。
求证:EF∥BC,EF= BC
1
2
可证得:△AEF≌△CGF
∠EAF=∠GCF
CG∥AB
CG=AE=EB
∴四边形EBCG是平行四边形。
EF∥BC
且EF= EG= BC
1
2
1
2
证法四:如图,过F作AB的平行线交BC于D,
过A作BC的平行线交FE于G。
G
D
证法三:延长EF到点G,使FG=EF,
连结AG、CG、EC
证得:四边形BCFD是平行四边形,
四边形ADCF是平行四边形。
G
证得:四边形ABDG是平行四边形,
四边形EBDF是平行四边形。
四边形AEFG是平行四边形。 △AFG≌△CFD
1. 如图,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm, E,F,H,M分别是边AB,BC,CD,DA的中点,则□EFHM 的周长 。
9.4 cm
2.已知△ABC的各边长度分别为3cm,3.4cm,4cm,求连结各边中
点所构成的△DEF的周长 。
5.2 cm
3.如图,两块相同的直角三角形完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△EBD的位置,点D在AC上,DE与AB相交于点F,则DF= .
2.5
A
B
C
D
E
F
在Rt△ABC中,∠A=30°,AC=10,
∴BC=5
∠C=60°,BC=BD, ∠ABD=30°,
∴ △BCD是等边三角形,△BCD是等腰三角形。
∴BC=BD=CD=AD,D是AC的中点。
∠C=∠EDB=60°, ∴∠ADF=60°
DF是△ABC的中位线,
DF= BC=2.5
1
2
例1 如图,□ABCD的周长为36.对角线AC,BD相交于点O.点E是CD的中点.BO=6.求△DOE的周长。
【解题思路】根据平行四边形的性质,对角线互相平分,两组对边分别相等,可以分别求出OD、OE+DE的长,即可求解.
∴△DOE的周长=OD+OE+DE=6+9=15
A
B
C
D
E
O
解:∵□ABCD的周长为36, ∴BC+CD=18,
∵四边形ABCD为平行四边形,
∴O是BD的中点, ∴OD=6,
又∵E是CD的中点,∴OE是△BCD的中位线,
∴OE+DE=9,
例2.求证:三角形的一条中位线与第三边上的中线互相平分.
已知,如图,△ABC中,D、E、F分别
是边AB、BC、CA的中点,DF、AE交
于点O,求证:DF与AE互相平分。
E
F
D
C
B
A
O
分析:根据“平行四边形对角线互相平分”的性质,只要能证明四边形ADEF是平行四边形即可。
又∵ DE、AE分别□ADEF的对角线。
∴ DF与AE互相平分。
证明:连接DE、EF
∵D、EF分别是AB、BC、AC中点
∴ DE∥AF,FE∥AD
∴ 四边形ADEF是平行四边形。
G
.
F
E
D
C
B
A
【解题思路】由条件,努力构造三角形中位线。取FC的中点G,连接DG。
这样F、G分别是AG、CF的中点。
例3.如图,AD是△ABC中线,E是AD的中点,BE交AC于F,AF= AC,试说明EF= BF
1
3
1
4
证明:取FC的中点G,连接DG
∵ AF= AC,
1
3
∴F、G是AC的三等分点。
又∵E是AD的中点,∴ EF= DG,
1
2
又∵D是BC的中点,∴ DG= BF,
1
2
1
4
∴ EF= DG= × BF= BF
1
2
1
2
1
2
A
B
C
D
E
F
1.已知: D、E、F分别为△ABC的边AB、AC、BC的中点。
(1)、已知DE=5,DF=4,EF=6,
则BC= ,AC= , AB= ,
△ DEF的周长= ,
△ ABC的周长= ,
△ ABC的周长是△DEF 周长的 ,
10
8
12
15
30
2倍
(2)、图中有 个平行四边形。
3
2.已知,如图,在△ABC中,AE=EC,AD⊥BC,EF⊥BC,BE=2EF,问AD与BE相等吗?为什么?
A
E
D
C
B
F
(3)连结AF,则AF是△ABC的 ,AF与DE 的关系是 。
(4)若△ABC的面积是 20,
则△DEF的面积是 ,
△DEF的面积是△ABC的面积的 。
中线
互相平分
5
1
4
结论:(1)三角形三条中位线围成的三角形周长是原
三角形周长的一半,面积是原三角形面积的四分之一。
(2)三角形的一条中位线与第三边上的中线互相平分。
A
B
C
D
E
F
AD=BE=2EF
3.已知:如图,AD是△ABC的高,M、N和E分别为AB、AC、BC的中点。
求证:EM=DN
N
M
E
D
C
B
A
提示:ME是△ABC的中位线,ME= AC.
1
2
N是Rt△ADC斜边AC的中点,DN是中线,DN= AC.
1
2
E
D
A
C
B
.
4.如图,在△ABC中,∠A=2∠B,CD⊥AB,E为AB的中点。求证:DE= AC
1
2
·
F
取BC的中点F,连接EF、DF
EF是△ABC的中位线,EF= AC,
1
2
∠A=∠FEB =2∠B,
∠FDE =∠B,
∠FDE =∠DFE,DE=EF
作业:p57 B 4、5、6
1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:
三角形的中位线平行与第三边,
并且等于它的一半。
E
D
C
B
A
3.应用三角形中位线的性质解决有关计算或
说理等问题时,根据条件,努力构造三角形中位线。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
