平行四边形的面积(课件)人教版五年级上册数学(共26张PPT)
文档属性
| 名称 | 平行四边形的面积(课件)人教版五年级上册数学(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 21:39:52 | ||
图片预览





文档简介
(共26张PPT)
平行四边形的面积
小故事
以前,有个地主,他给两个儿子分地,给大儿子分长方形的地,给小儿子分平行四边形的地,可是两个儿子都认为分给自己的那块地小,都说老地主偏心。
谁分到的地更大呢?
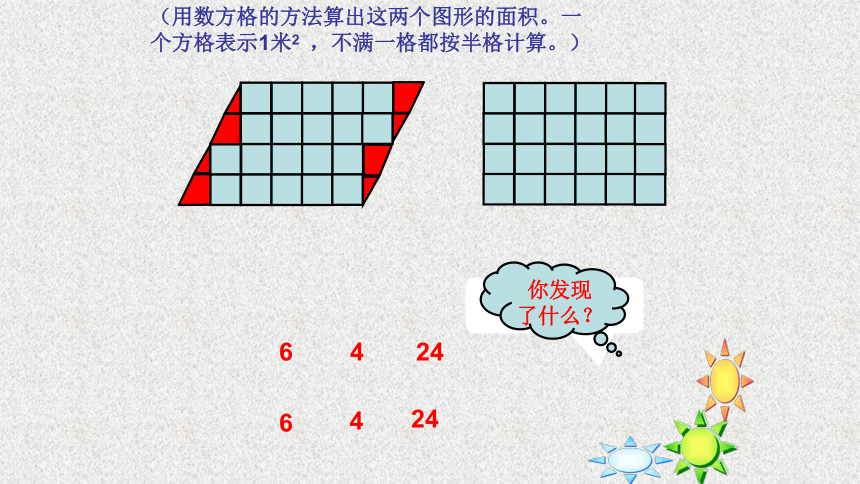
6
4
6
4
24
24
你发现了什么?
(用数方格的方法算出这两个图形的面积。一个方格表示1米2 ,不满一格都按半格计算。)
平行四边形的底和长方形的长相等
平行四边形的高和长方形的宽相等
平行四边形的面积和长方形的面积相等
我发现:
说说你的猜想!
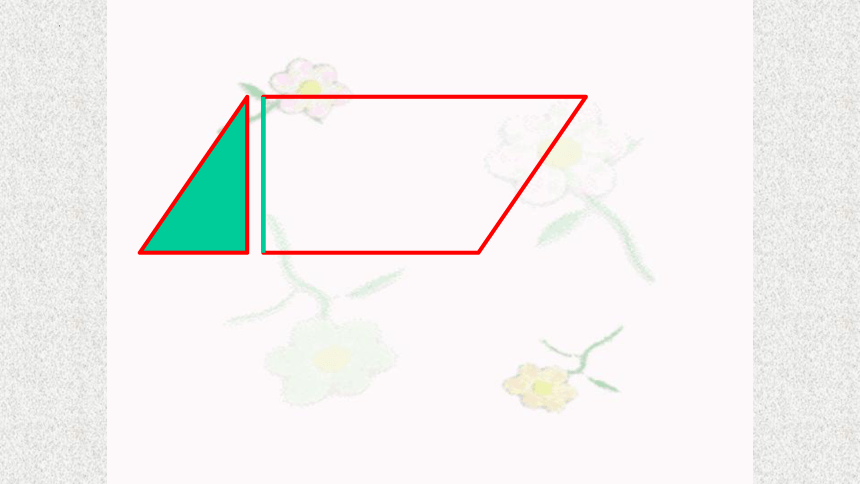
第一步:动手操作。为了剪拼的规范,建议大家用铅笔和三角板先画一画,再剪拼
第二步:结合剪拼过程,思考这两个问题
1、剪拼后的长方形和原来平行四边形比,( )变了,( )不变。
2、长方形的长和宽与平行四边形的底和高有什么关系?
第三步:把你的剪拼方法及你对这两个问题的思考和小组同学进行交流
验证步骤
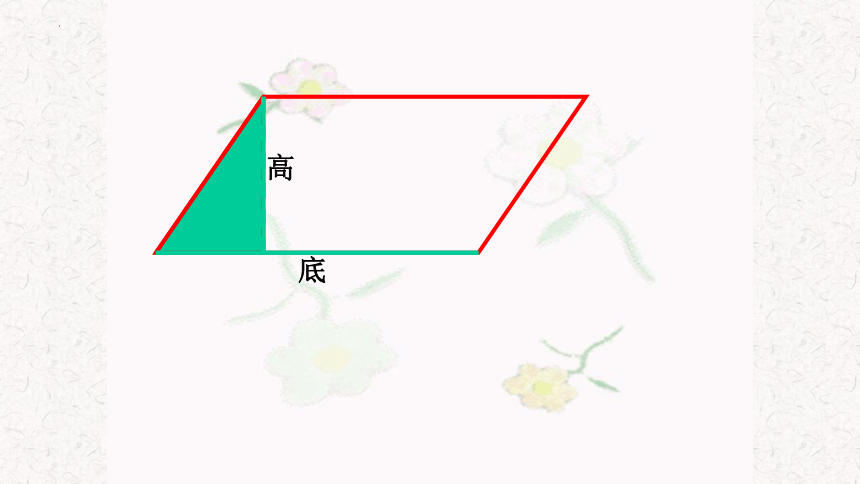
高
底
高
底
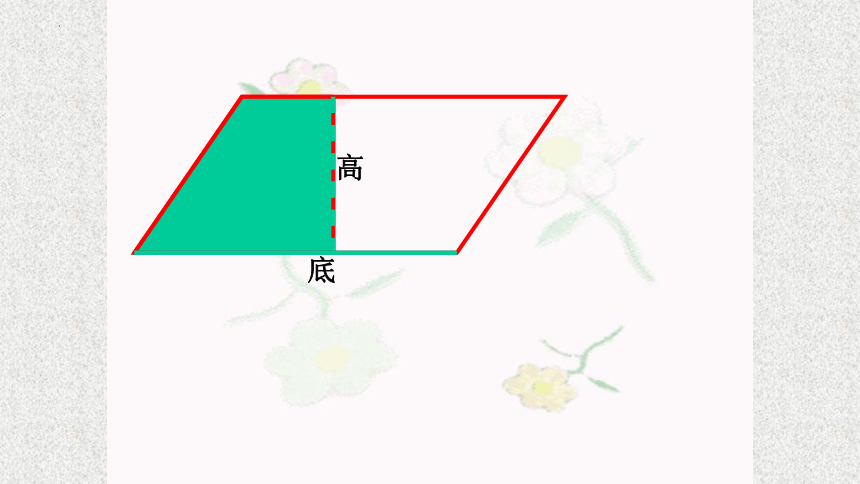
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
高
底
宽
长
2、平行四边形的 和长方形的 相等.
高
宽
底
长
平行四边形
变成了
长方形
所以:平行四边形的面积就=
底
×
高
3、平行四边形的 和长方形的 相等.
因 为: 长 方 形 的 面 积= 长 × 宽
1、剪拼后的长方形和原来平行四边形比,( )变了,( )不变
形状
面积
用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高。那么平行四边形的面积公式就可以写成:
S=a ×h
=a ·h
=a h
平行四边形的面积=底×高
想一想:求平行四边形的面积必须
知道哪两个条件?
必须知道平行四边形的底和对应(垂直)的高。
S =ah
=6 × 4
= 24(m2)
平行四边形花坛的底是6m,高是 4m,它的面积是少?
6m
4m
答:它的面积是 24 m2。
例1
做一做
下面平行四边形的面积是:( )
30分米
20分米
25分米
A:30×25=750平方分米
B:25×20=500平方分米
C:30×20=600平方分米
C
做一做
口算出下面每个平行四边形的面积:
3cm
2cm
2.4cm
1.6cm
5.2cm
3.6cm
4cm
3cm
面积公式当中的底和高必须是相对应的
注意:
一、计算下面每个平行四边形的面积。
(1)底=8分米 ,高=9分米
(2) a=25厘米,h=4厘米
巩固练习
二、选择:
(1)已知一个平行四边形的底是2米,高是5分米,它的面积是( )。
A、10平方米 B、100平方分米 C、100分米
(2)已知一个平行四边形的面积是30平方米,底是6米,高是( )。
A、180平方米 B、5平方米 C、5米
(3)A、B、C中哪一个的面积是3×2=6平方厘米( )。
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
B
C
C
三、判断:
①平行四边形的底越长,面积越大。( )
②平行四边形的面积等于长方形的面积( )
③下图中两个平行四边形的面积相等。( )
2厘米
2.5厘米
×
×
√
同 底等高的平行四边形面积相等
(等)
通过今天的学习,你有什么收获?
小 结
1、我们学行四边形的面积计算公式:
平行四边形的面积=底×高
S = a × h=a·h =ah
2、求平行四边形的面积必须知道平行四边形
的底和对应的高。
3、在推导公式的过程中我们用了一种很好的方法--- 割补法(沿着高来割补)---把平行四边形通过割 ---移---补---变成长方形。
平行四边形的面积
小故事
以前,有个地主,他给两个儿子分地,给大儿子分长方形的地,给小儿子分平行四边形的地,可是两个儿子都认为分给自己的那块地小,都说老地主偏心。
谁分到的地更大呢?
6
4
6
4
24
24
你发现了什么?
(用数方格的方法算出这两个图形的面积。一个方格表示1米2 ,不满一格都按半格计算。)
平行四边形的底和长方形的长相等
平行四边形的高和长方形的宽相等
平行四边形的面积和长方形的面积相等
我发现:
说说你的猜想!
第一步:动手操作。为了剪拼的规范,建议大家用铅笔和三角板先画一画,再剪拼
第二步:结合剪拼过程,思考这两个问题
1、剪拼后的长方形和原来平行四边形比,( )变了,( )不变。
2、长方形的长和宽与平行四边形的底和高有什么关系?
第三步:把你的剪拼方法及你对这两个问题的思考和小组同学进行交流
验证步骤
高
底
高
底
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
高
底
宽
长
2、平行四边形的 和长方形的 相等.
高
宽
底
长
平行四边形
变成了
长方形
所以:平行四边形的面积就=
底
×
高
3、平行四边形的 和长方形的 相等.
因 为: 长 方 形 的 面 积= 长 × 宽
1、剪拼后的长方形和原来平行四边形比,( )变了,( )不变
形状
面积
用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高。那么平行四边形的面积公式就可以写成:
S=a ×h
=a ·h
=a h
平行四边形的面积=底×高
想一想:求平行四边形的面积必须
知道哪两个条件?
必须知道平行四边形的底和对应(垂直)的高。
S =ah
=6 × 4
= 24(m2)
平行四边形花坛的底是6m,高是 4m,它的面积是少?
6m
4m
答:它的面积是 24 m2。
例1
做一做
下面平行四边形的面积是:( )
30分米
20分米
25分米
A:30×25=750平方分米
B:25×20=500平方分米
C:30×20=600平方分米
C
做一做
口算出下面每个平行四边形的面积:
3cm
2cm
2.4cm
1.6cm
5.2cm
3.6cm
4cm
3cm
面积公式当中的底和高必须是相对应的
注意:
一、计算下面每个平行四边形的面积。
(1)底=8分米 ,高=9分米
(2) a=25厘米,h=4厘米
巩固练习
二、选择:
(1)已知一个平行四边形的底是2米,高是5分米,它的面积是( )。
A、10平方米 B、100平方分米 C、100分米
(2)已知一个平行四边形的面积是30平方米,底是6米,高是( )。
A、180平方米 B、5平方米 C、5米
(3)A、B、C中哪一个的面积是3×2=6平方厘米( )。
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
B
C
C
三、判断:
①平行四边形的底越长,面积越大。( )
②平行四边形的面积等于长方形的面积( )
③下图中两个平行四边形的面积相等。( )
2厘米
2.5厘米
×
×
√
同 底等高的平行四边形面积相等
(等)
通过今天的学习,你有什么收获?
小 结
1、我们学行四边形的面积计算公式:
平行四边形的面积=底×高
S = a × h=a·h =ah
2、求平行四边形的面积必须知道平行四边形
的底和对应的高。
3、在推导公式的过程中我们用了一种很好的方法--- 割补法(沿着高来割补)---把平行四边形通过割 ---移---补---变成长方形。
