第二章 二次函数单元质量检测试卷B(含答案)
文档属性
| 名称 | 第二章 二次函数单元质量检测试卷B(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 19:50:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年九年级(下)第二章二次函数检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 下列二次函数中,图象以直线 为对称轴,且经过点 的是
A. B.
C. D.
2. 对于二次函数 的图象,下列说法不正确的是
A. 开口向下
B. 对称轴是直线
C. 顶点坐标为
D. 当 时, 随 的增大而减小
3. 如图,二次函数 的图象与 轴相交于 和 两点,当函数值 时,自变量 的取值范围是
A. B.
C. D. 或
4. 根据下列表格的对应值:
判断方程 (,,, 为常数)的一个解 的取值范围是
A. B. C. D.
5. 将二次函数 化成 的形式是
A. B.
C. D.
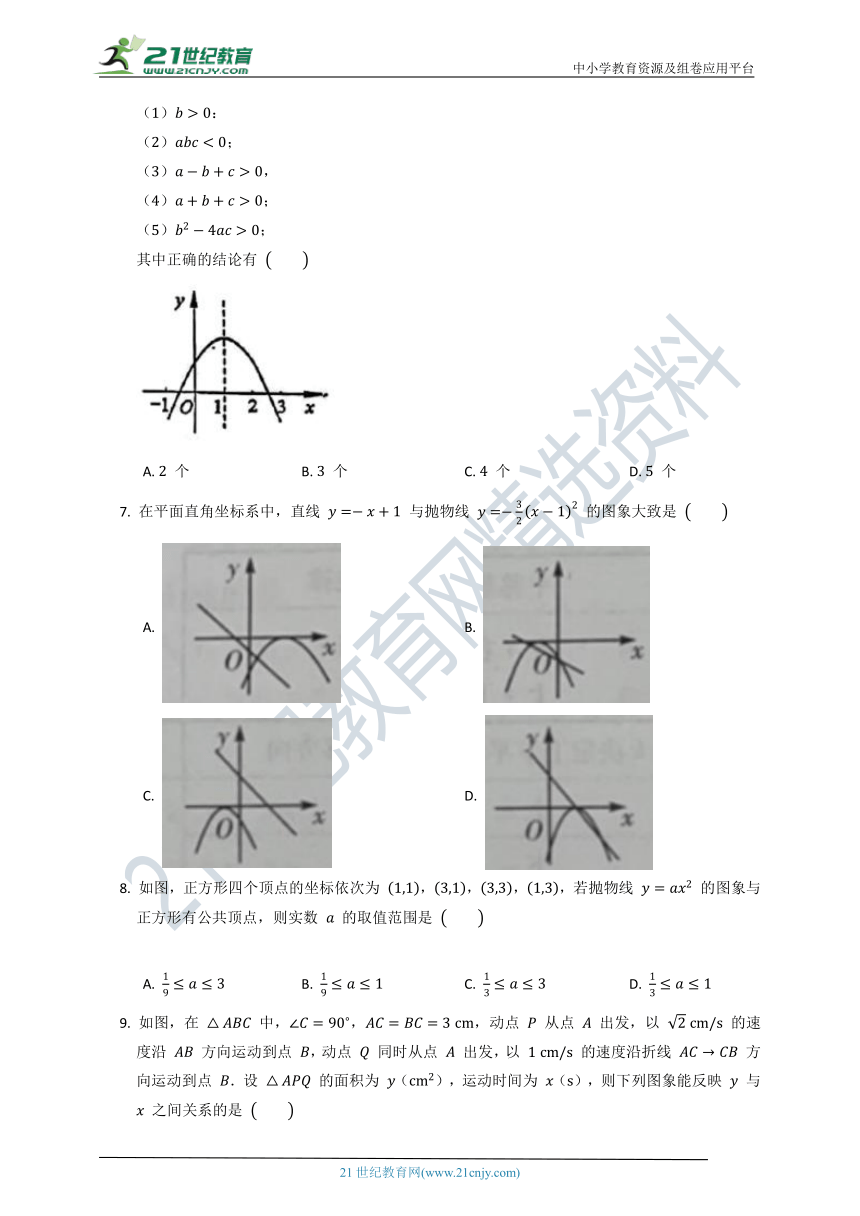
6. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
7. 在平面直角坐标系中,直线 与抛物线 的图象大致是
A. B.
C. D.
8. 如图,正方形四个顶点的坐标依次为 ,,,,若抛物线 的图象与正方形有公共顶点,则实数 的取值范围是
A. B. C. D.
9. 如图,在 中,,,动点 从点 出发,以 的速度沿 方向运动到点 ,动点 同时从点 出发,以 的速度沿折线 方向运动到点 .设 的面积为 (),运动时间为 (),则下列图象能反映 与 之间关系的是
A. B.
C. D.
10. 若抛物线 与抛物线 关于直线 对称,则 , 的值为
A. , B. , C. , D. ,
11. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为 ,当水面离桥拱顶的高度 是 时,这时水面宽度 为
A. B. C. D.
12. 【摸底测试 】
如图,已知二次函数 的图象如图所示,有下列 个结论:① ;② ;③ ;④ ;⑤ ( 的实数).其中正确结论的有
A. ①②③ B. ②③⑤ C. ②③④ D. ③④⑤
二、填空题(共6小题;每小题4分,共24分)
13. 若抛物线 经过 ,则该抛物线的解析式为 .
14. 如果某抛物线开口方向与抛物线 的开口方向相同,那么该抛物线有最 点(填“高”或“低”)
15. 已知二次函数 ,当 分别取 , 时,函数值相等,则当 取 时,函数值为 .
16. 若抛物线 的顶点为 ,抛物线 的顶点为 ,且满足顶点 在抛物线 上,顶点 在抛物线 上,则称抛物线 与抛物线 互为“关联抛物线”,已知顶点为 的抛物线 与顶点为 的抛物线互为“关联抛物线”,直线 与 轴正半轴交于点 ,如果 ,那么顶点为 的抛物线的表达式为 .
17. 某火箭竖直向上发射时,它的高度 与时间 的关系可以用函数表达式 表示.经过 ,该火箭达到它的最高点.
18. 某商店销售一批头盔,售价为每顶 元,每月可售出 顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价 元,每月可多售出 顶.已知头盔的进价为每顶 元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
三、解答题(共7小题;共60分)
19. (8分)已知抛物线 上部分点的横坐标 与纵坐标 的对应值如下表:
(1)求该抛物线的表达式;
(2)将抛物线 沿 轴向右平移 个单位,使得新抛物线经过原点 ,求 的值以及新抛物线的表达式.
20. (8分)观察函数 的图象和函数 的图象,写出它们的两个不同特征.
21. (8分)已知抛物线 与 轴交于点 ,,且过点 .
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线 上,并写出平移后抛物线的解析式.
22. (10分)已知二次函数 .
(1)求证:不论 为任何实数,此二次函数的图象与 轴都有两个交点.
(2)当二次函数的图象经过点 时,确定 的值.并写出此二次函数与 轴的交点坐标.
23. (8分)填表:
24. (8分)下列函数中,如果是二次函数,请把它化为一般式并指出相应的 ,, 的值.
(1);
(2);
(3);
(4).
25. (10分)已知 是常数,抛物线 的对称轴是 轴,并且与 轴有两个交点.
(1)求 的值;
(2)若点 在抛物线 上,且点 到 轴的距离是 ,求点 的坐标.
答案
一 选择题
1. C
2. B
3. D
4. C
5. A
6. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
7. D
8. A
【解析】抛物线 的图象与正方形有公共顶点,
又抛物线经过 时,,经过点 时,,
所以 ,故选A.
9. D
【解析】过点 作 于点 ,
①如图 ,
当点 在 上运动时,即 ,
由题意知 ,,
,
,
则 ;
②如图 ,
当点 在 上运动时,即 ,此时点 与点 重合,
由题意知 ,,
,
,
则 .
10. C
【解析】由抛物线 可知抛物线 的对称轴为直线 ,交 轴于点 ,
抛物线 的对称轴为直线 ,
抛物线 与抛物线 关于直线 对称,
,
解得 ,
点 关于直线 的点 在抛物线 上,
把点 代入得 ,
解得 ,
故选:C.
11. D
【解析】根据题意,当 时,有 ,
解得:,
,,
所有水面宽度 .
12. B
【解析】① 对称轴在 轴的右侧,
,
由图象可知:,
,故①不正确;
②当 时,,
,故②正确;
③由对称知,当 时,函数值大于 ,即 ,故③正确;
④ ,
,
,
,,故④不正确;
⑤当 时, 的值最大.此时,,
而当 时,,
,
故 ,即 ,故⑤正确.
故②③⑤正确.
故选:B.
二 填空题
13.
【解析】把 代入 得:
,
解得:,
抛物线的解析式为:.
14. 低
【解析】 抛物线开口方向与抛物线 的开口方向相同,抛物线 中, 开口方向向上,
该抛物线有最低点.
15.
【解析】 二次函数 的图象的对称轴为直线 , 分别取 , 时函数值相等,
,
当 取 ,即 取 时,函数值为 .
16.
【解析】设顶点为 的抛物线顶点坐标 为 ,
已知抛物线 的顶点坐标 为 ,
,
,即 ,解得 ,
直线 与 轴正半轴交于点 ,
点坐标为 ,
则直线 解析式为 ,
点在直线 上, 点也在抛物线 ,
故有 化简得
联立得 ,
化简得 ,
解得 或 (舍),
将 代入 有 ,
解得 故 点坐标为 ,
则顶点为 的抛物线的表达式为 ,
将 代入 有 ,
化简得 ,解得 ,
故顶点为 的抛物线的表达式为 .
17.
18.
【解析】设每顶头盔的售价为 元,获得的利润为 元,
当 时, 取得最大值,此时 ,故答案为:.
三 解答题
19. (1) ,;,,
抛物线的对称轴为直线 ,则抛物线的顶点坐标为 ,
设抛物线解析式为 ,
把 代入得 ,解得 ,
抛物线解析式为 .
(2) 将抛物线 沿 轴向右平移 个单位,得到 ,
经过原点,
,解得 ,(舍去),
,
新抛物线的表达式为 .
20. 答案不唯一.
二次函数 的图象开口方向向上,有最低点,当 时,随着 值的增大, 值增大;当 时,随着 值的增大, 值减小,
二次函数 的图象开口方向向下,有最高点,当 时,随着 值的增大, 值减小;当 时,随着 值的增大, 值增大.
21. (1) 抛物线与 轴交于点 ,,
可设抛物线解析式为 ,
把 代入得:,
解得:,
故抛物线解析式为 ,
即 ,
,
顶点坐标 .
(2) 先向左平移 个单位,再向下平移 个单位,得到的抛物线的解析式为 ,平移后抛物线的顶点为 落在直线 上(答案不唯一).
22. (1) ,
不论 为任何实数,此二次函数的图象与 轴都有两个交点.
(2) 依题意得
解得
,
当 时,有
解得
此二次函数与 轴的交点坐标为 和 .
23.
【解析】抛物线 的对称轴是直线 ,顶点坐标是 ,当 时,开口向上;当 时,开口向下.
24. (1) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
(2) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
(3) 该函数不是二次函数.
(4) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
25. (1) 抛物线 的对称轴是 轴,
,解得 ,,
又 抛物线 与 轴有两个交点,
,
.
(2) 将 代入抛物线的解析式可得 ,
点 在抛物线 上,且点 到 轴的距离是 ,
点 的横坐标为 或 ,
当 时,,
当 时,.
点 的坐标为 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年九年级(下)第二章二次函数检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 下列二次函数中,图象以直线 为对称轴,且经过点 的是
A. B.
C. D.
2. 对于二次函数 的图象,下列说法不正确的是
A. 开口向下
B. 对称轴是直线
C. 顶点坐标为
D. 当 时, 随 的增大而减小
3. 如图,二次函数 的图象与 轴相交于 和 两点,当函数值 时,自变量 的取值范围是
A. B.
C. D. 或
4. 根据下列表格的对应值:
判断方程 (,,, 为常数)的一个解 的取值范围是
A. B. C. D.
5. 将二次函数 化成 的形式是
A. B.
C. D.
6. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
7. 在平面直角坐标系中,直线 与抛物线 的图象大致是
A. B.
C. D.
8. 如图,正方形四个顶点的坐标依次为 ,,,,若抛物线 的图象与正方形有公共顶点,则实数 的取值范围是
A. B. C. D.
9. 如图,在 中,,,动点 从点 出发,以 的速度沿 方向运动到点 ,动点 同时从点 出发,以 的速度沿折线 方向运动到点 .设 的面积为 (),运动时间为 (),则下列图象能反映 与 之间关系的是
A. B.
C. D.
10. 若抛物线 与抛物线 关于直线 对称,则 , 的值为
A. , B. , C. , D. ,
11. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为 ,当水面离桥拱顶的高度 是 时,这时水面宽度 为
A. B. C. D.
12. 【摸底测试 】
如图,已知二次函数 的图象如图所示,有下列 个结论:① ;② ;③ ;④ ;⑤ ( 的实数).其中正确结论的有
A. ①②③ B. ②③⑤ C. ②③④ D. ③④⑤
二、填空题(共6小题;每小题4分,共24分)
13. 若抛物线 经过 ,则该抛物线的解析式为 .
14. 如果某抛物线开口方向与抛物线 的开口方向相同,那么该抛物线有最 点(填“高”或“低”)
15. 已知二次函数 ,当 分别取 , 时,函数值相等,则当 取 时,函数值为 .
16. 若抛物线 的顶点为 ,抛物线 的顶点为 ,且满足顶点 在抛物线 上,顶点 在抛物线 上,则称抛物线 与抛物线 互为“关联抛物线”,已知顶点为 的抛物线 与顶点为 的抛物线互为“关联抛物线”,直线 与 轴正半轴交于点 ,如果 ,那么顶点为 的抛物线的表达式为 .
17. 某火箭竖直向上发射时,它的高度 与时间 的关系可以用函数表达式 表示.经过 ,该火箭达到它的最高点.
18. 某商店销售一批头盔,售价为每顶 元,每月可售出 顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价 元,每月可多售出 顶.已知头盔的进价为每顶 元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
三、解答题(共7小题;共60分)
19. (8分)已知抛物线 上部分点的横坐标 与纵坐标 的对应值如下表:
(1)求该抛物线的表达式;
(2)将抛物线 沿 轴向右平移 个单位,使得新抛物线经过原点 ,求 的值以及新抛物线的表达式.
20. (8分)观察函数 的图象和函数 的图象,写出它们的两个不同特征.
21. (8分)已知抛物线 与 轴交于点 ,,且过点 .
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线 上,并写出平移后抛物线的解析式.
22. (10分)已知二次函数 .
(1)求证:不论 为任何实数,此二次函数的图象与 轴都有两个交点.
(2)当二次函数的图象经过点 时,确定 的值.并写出此二次函数与 轴的交点坐标.
23. (8分)填表:
24. (8分)下列函数中,如果是二次函数,请把它化为一般式并指出相应的 ,, 的值.
(1);
(2);
(3);
(4).
25. (10分)已知 是常数,抛物线 的对称轴是 轴,并且与 轴有两个交点.
(1)求 的值;
(2)若点 在抛物线 上,且点 到 轴的距离是 ,求点 的坐标.
答案
一 选择题
1. C
2. B
3. D
4. C
5. A
6. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
7. D
8. A
【解析】抛物线 的图象与正方形有公共顶点,
又抛物线经过 时,,经过点 时,,
所以 ,故选A.
9. D
【解析】过点 作 于点 ,
①如图 ,
当点 在 上运动时,即 ,
由题意知 ,,
,
,
则 ;
②如图 ,
当点 在 上运动时,即 ,此时点 与点 重合,
由题意知 ,,
,
,
则 .
10. C
【解析】由抛物线 可知抛物线 的对称轴为直线 ,交 轴于点 ,
抛物线 的对称轴为直线 ,
抛物线 与抛物线 关于直线 对称,
,
解得 ,
点 关于直线 的点 在抛物线 上,
把点 代入得 ,
解得 ,
故选:C.
11. D
【解析】根据题意,当 时,有 ,
解得:,
,,
所有水面宽度 .
12. B
【解析】① 对称轴在 轴的右侧,
,
由图象可知:,
,故①不正确;
②当 时,,
,故②正确;
③由对称知,当 时,函数值大于 ,即 ,故③正确;
④ ,
,
,
,,故④不正确;
⑤当 时, 的值最大.此时,,
而当 时,,
,
故 ,即 ,故⑤正确.
故②③⑤正确.
故选:B.
二 填空题
13.
【解析】把 代入 得:
,
解得:,
抛物线的解析式为:.
14. 低
【解析】 抛物线开口方向与抛物线 的开口方向相同,抛物线 中, 开口方向向上,
该抛物线有最低点.
15.
【解析】 二次函数 的图象的对称轴为直线 , 分别取 , 时函数值相等,
,
当 取 ,即 取 时,函数值为 .
16.
【解析】设顶点为 的抛物线顶点坐标 为 ,
已知抛物线 的顶点坐标 为 ,
,
,即 ,解得 ,
直线 与 轴正半轴交于点 ,
点坐标为 ,
则直线 解析式为 ,
点在直线 上, 点也在抛物线 ,
故有 化简得
联立得 ,
化简得 ,
解得 或 (舍),
将 代入 有 ,
解得 故 点坐标为 ,
则顶点为 的抛物线的表达式为 ,
将 代入 有 ,
化简得 ,解得 ,
故顶点为 的抛物线的表达式为 .
17.
18.
【解析】设每顶头盔的售价为 元,获得的利润为 元,
当 时, 取得最大值,此时 ,故答案为:.
三 解答题
19. (1) ,;,,
抛物线的对称轴为直线 ,则抛物线的顶点坐标为 ,
设抛物线解析式为 ,
把 代入得 ,解得 ,
抛物线解析式为 .
(2) 将抛物线 沿 轴向右平移 个单位,得到 ,
经过原点,
,解得 ,(舍去),
,
新抛物线的表达式为 .
20. 答案不唯一.
二次函数 的图象开口方向向上,有最低点,当 时,随着 值的增大, 值增大;当 时,随着 值的增大, 值减小,
二次函数 的图象开口方向向下,有最高点,当 时,随着 值的增大, 值减小;当 时,随着 值的增大, 值增大.
21. (1) 抛物线与 轴交于点 ,,
可设抛物线解析式为 ,
把 代入得:,
解得:,
故抛物线解析式为 ,
即 ,
,
顶点坐标 .
(2) 先向左平移 个单位,再向下平移 个单位,得到的抛物线的解析式为 ,平移后抛物线的顶点为 落在直线 上(答案不唯一).
22. (1) ,
不论 为任何实数,此二次函数的图象与 轴都有两个交点.
(2) 依题意得
解得
,
当 时,有
解得
此二次函数与 轴的交点坐标为 和 .
23.
【解析】抛物线 的对称轴是直线 ,顶点坐标是 ,当 时,开口向上;当 时,开口向下.
24. (1) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
(2) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
(3) 该函数不是二次函数.
(4) 该函数是二次函数.
,
该函数的一般式为 ,其中 ,,.
25. (1) 抛物线 的对称轴是 轴,
,解得 ,,
又 抛物线 与 轴有两个交点,
,
.
(2) 将 代入抛物线的解析式可得 ,
点 在抛物线 上,且点 到 轴的距离是 ,
点 的横坐标为 或 ,
当 时,,
当 时,.
点 的坐标为 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
