9.2液体的压强 习题课课件(共29张PPT) 2022-2023学年人教版八年级下册物理
文档属性
| 名称 | 9.2液体的压强 习题课课件(共29张PPT) 2022-2023学年人教版八年级下册物理 |  | |
| 格式 | pptx | ||
| 文件大小 | 1000.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-04 10:22:53 | ||
图片预览



文档简介
(共29张PPT)
第九章:压强
液体的压强 习题课
初中物理人教版
物理
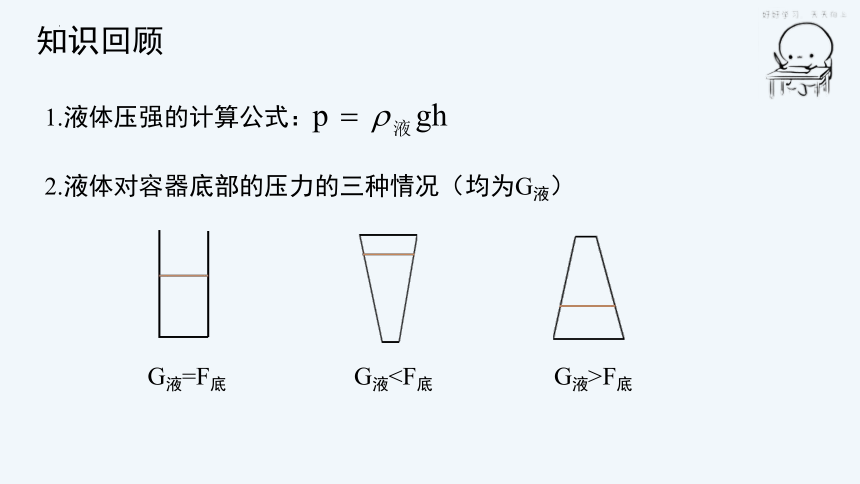
知识回顾
1.液体压强的计算公式:
2.液体对容器底部的压力的三种情况(均为G液)
G液=F底
G液>F底
G液一、液体压强计算公式的运用
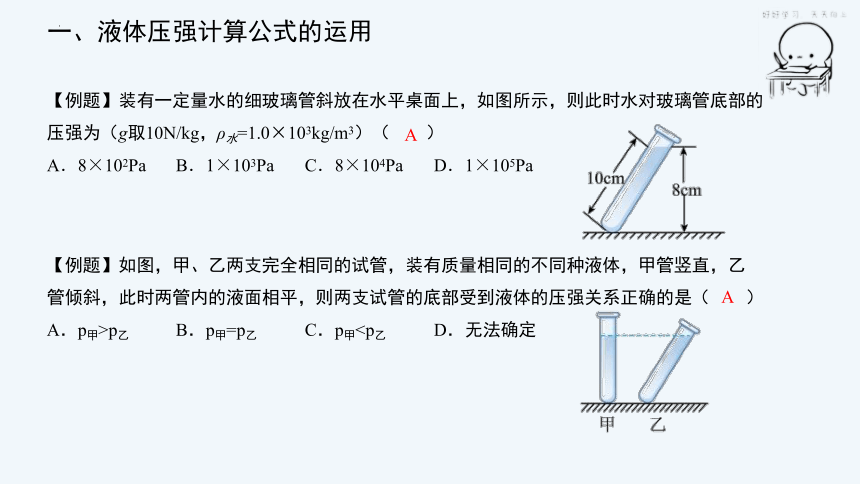
【例题】装有一定量水的细玻璃管斜放在水平桌面上,如图所示,则此时水对玻璃管底部的压强为(g取10N/kg,ρ水=1.0×103kg/m3)( )
A.8×102Pa B.1×103Pa C.8×104Pa D.1×105Pa
【例题】如图,甲、乙两支完全相同的试管,装有质量相同的不同种液体,甲管竖直,乙管倾斜,此时两管内的液面相平,则两支试管的底部受到液体的压强关系正确的是( )
A.p甲>p乙 B.p甲=p乙 C.p甲A
A
一、液体压强计算公式的运用
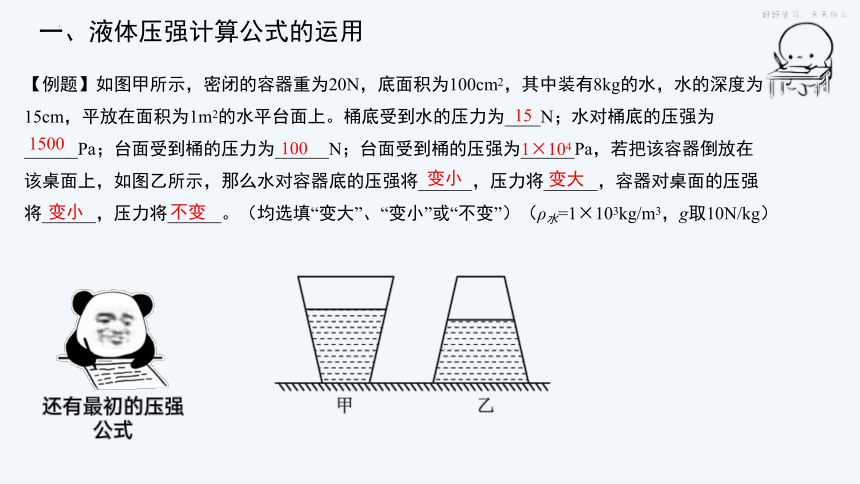
【例题】如图甲所示,密闭的容器重为20N,底面积为100cm2,其中装有8kg的水,水的深度为15cm,平放在面积为1m2的水平台面上。桶底受到水的压力为____N;水对桶底的压强为______Pa;台面受到桶的压力为______N;台面受到桶的压强为______Pa,若把该容器倒放在该桌面上,如图乙所示,那么水对容器底的压强将______,压力将______,容器对桌面的压强将______,压力将______。(均选填“变大”、“变小”或“不变”)(ρ水=1×103kg/m3,g取10N/kg)
15
1500
100
1×104
变小
变大
变小
不变
一、液体压强计算公式的运用(升级)
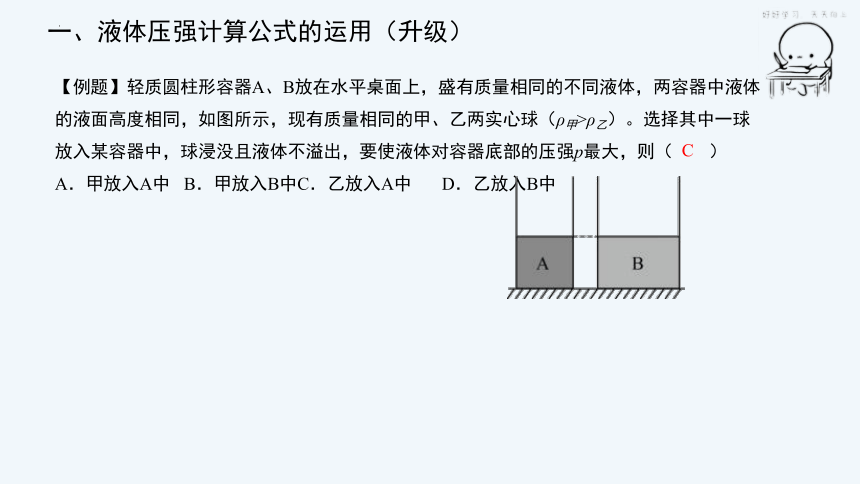
【例题】轻质圆柱形容器A、B放在水平桌面上,盛有质量相同的不同液体,两容器中液体的液面高度相同,如图所示,现有质量相同的甲、乙两实心球(ρ甲>ρ乙)。选择其中一球放入某容器中,球浸没且液体不溢出,要使液体对容器底部的压强p最大,则( )
A.甲放入A中 B.甲放入B中C.乙放入A中 D.乙放入B中
C
一、液体压强计算公式的运用(升级)
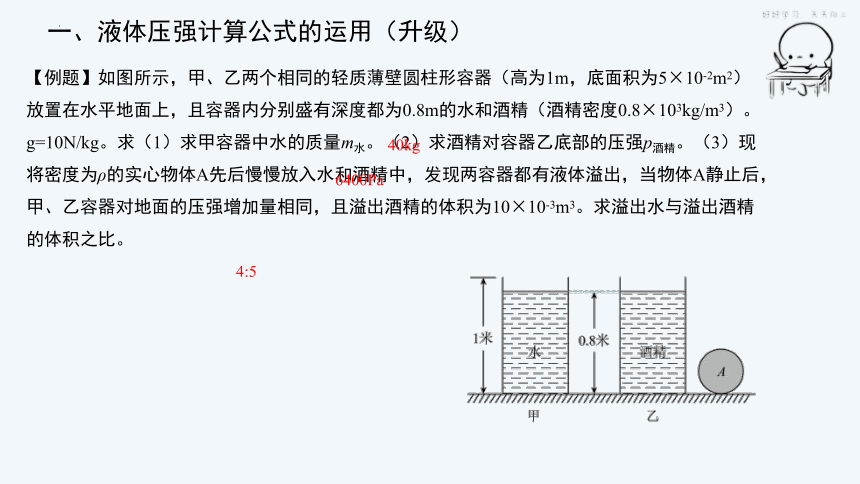
【例题】如图所示,甲、乙两个相同的轻质薄壁圆柱形容器(高为1m,底面积为5×10-2m2)放置在水平地面上,且容器内分别盛有深度都为0.8m的水和酒精(酒精密度0.8×103kg/m3)。
g=10N/kg。求(1)求甲容器中水的质量m水。(2)求酒精对容器乙底部的压强p酒精。(3)现将密度为ρ的实心物体A先后慢慢放入水和酒精中,发现两容器都有液体溢出,当物体A静止后,甲、乙容器对地面的压强增加量相同,且溢出酒精的体积为10×10-3m3。求溢出水与溢出酒精的体积之比。
40kg
6400Pa
4:5
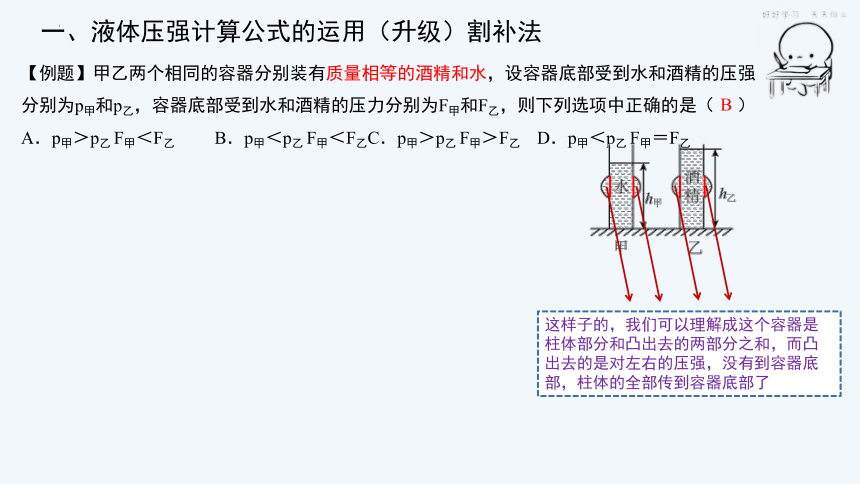
【例题】甲乙两个相同的容器分别装有质量相等的酒精和水,设容器底部受到水和酒精的压强分别为p甲和p乙,容器底部受到水和酒精的压力分别为F甲和F乙,则下列选项中正确的是( )
A.p甲>p乙 F甲<F乙 B.p甲<p乙 F甲<F乙C.p甲>p乙 F甲>F乙 D.p甲<p乙 F甲=F乙
一、液体压强计算公式的运用(升级)割补法
这样子的,我们可以理解成这个容器是柱体部分和凸出去的两部分之和,而凸出去的是对左右的压强,没有到容器底部,柱体的全部传到容器底部了
B
一、液体压强计算公式的运用(升级)割补法
【例题】在两个完全相同的容器中分别倒入甲和乙两种不同的液体,如图所示,下列分析正确的是( )
A.若甲和乙的质量相等,则甲的密度小于乙的密度B.若甲和乙对容器底部的压强相等,则甲的密度小于乙的密度C.若甲和乙对容器底部的压强相等,则甲的质量小于乙的质量D.若甲和乙的质量相等,则甲对容器底部的压强小于乙对容器底部的压强
①
⑤
⑥
④
②
③
C
解析的等效图
用基本公式法的时候,要注意:有时候整体代换很重要
二、抽倒液体
【例题】如图所示,底面积不同的薄壁圆柱形容器A和B分别盛有甲、乙两种液体,两液面保持相平。现从两容器中抽出部分液体后,其液面仍保持相平,若此时甲对A底部的压力大于乙对B底部的压力,则抽取前,甲、乙各自对容器底部的压强pA、pB和压力FA、FB的关系是( )
A.pA<pB,FA<FB B. pA<pB,FA>FBC. pA>pB,FA<FB D. pA>pB,FA>FB
二、抽倒液体
D
二、抽倒液体
【例题】底面积不同的圆柱形容器A和B原先分别盛有体积相同的甲、乙两种液体,如图所示,现从容器中分别抽出部分液体后,液体对各自容器底部的压强为p甲、p乙,则下列做法中,符合实际的是( )
A.若液体原先对容器底部的压力相等,则抽出相等质量的液体后,p甲一定等于p乙B.若液体原先对容器底部的压力相等,则抽出相等厚度的液体后,p甲可能大于p乙C.若液体原先对容器底部的压强相等,则抽出相等体积的液体后,p甲一定等于p乙D.若液体原先对容器底部的压强相等,则抽出相等厚度的液体后,p甲一定等于p乙
C
【例题】如图所示,两薄壁圆柱形容器内分别盛有甲、乙两种液体放置在水平地面上,现从两容器中分别抽出部分液体,使甲、乙剩余部分的深度均为h,若此时两液体对容器底部的压力相等;则甲、乙抽出部分的质量m甲、m乙及液体对容器底部压强变化p甲、p乙的大小关系是( )
A.m甲<m乙, p甲>p乙 B.m甲>m乙, p甲>p乙C.m甲=m乙, p甲<p乙 D.m甲<m乙, p甲<p乙
二、抽倒液体
D
二、抽倒液体
【例题】如图所示,底面积不同的圆柱形容器分别盛有甲、乙两种液体,液体对各自容器底部的压力相等。现分别从两容器中抽出液体,且剩余液体的液面到容器底部的距离均为h,则剩余液体对各自容器底部的压强p、压力F的关系是( )
A.p甲 F乙 B.p甲=p乙;F甲< F乙
C.p甲>p乙;F甲> F乙 D.p甲D
二、抽倒液体
【例题】如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有水和酒精(ρ水>ρ酒精),且两种液体对容器底部的压强相等。一定能使水对容器底部的压强大于酒精对容器底部压强的方法是( )
A.倒入相同质量的水和酒精 B.倒入相同体积的水和酒C.抽出相同质量的水和酒精 D.抽出相同体积的水和酒精
C
C
二、抽倒液体(能力提升)
【例题】如图所示,A、B 两个柱形容器(SA>SB,容器足够高),分别盛有质量相同的甲、乙两种液体,则下列说法正确的是( )
A.分别向A、B 容器中倒入相同质量的甲、乙液体后,液体对容器底部的压强 p 甲可能等于 p 乙B.分别从A、B 容器中抽出相同体积的甲、乙液体后,液体对容器底部的压强 p 甲一定大于 p 乙C.分别向A、B 容器中倒入相同高度的甲、乙液体后,液体对容器底部的压力 F 甲一定小于 F 乙D.分别从A、B 容器中抽出相同高度的甲、乙液体后,液体对容器底部的压强 p 甲一定大于 p 乙
【例题】如图所示,往装有水的容器内匀速下插一长方体物体(未触底),容器中水面逐渐上升,容器底面受到水的压强p随时间t变化的曲线,较合理的是( )
三、图像问题
C
【例题】如图甲所示的容器放置在水平地面上,该容器上、下两部分都是圆柱形,其横截面积分别为S1、S2,容器底部装有控制阀门。容器内装有密度为0.8×103kg/m3的液体,液体通过控制阀门匀速排出的过程中,容器底部受到液体的压强P随时间t变化关系如图乙所示。则阀门打开前液体的深度H=_______cm,上、下两部分横截面积之比S1:S2=_______。(g取10N/kg)
三、图像问题
15
1:4
【例题】如图,实心圆柱体甲、乙的密度均为3×103 kg/m3,甲的质量为6 kg,底面积为200 cm2;乙的质量为12kg,底面积为300 cm2。水平地面上的轻质薄壁容器丙内盛有9 cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000 cm2。若把甲沿水平方向切割的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度与切割的高度的部分关系如图丁所示(g=10N/kg)。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9 cm深水的容器丙中,此时容器丙对水平地面的压强。
三、图像问题(能力提升)
2000cm3
90N
1940Pa
解析
解析
四、液面变化问题
【例题】如图所示,圆柱体甲和轻质薄壁圆柱形容器乙置于水平地面。甲的质量为4kg,乙容器的底面积为2×10-2m2,内有0.2m深的水。(g取10N / kg )
(1)求甲对地面的压力F甲。
(2)求水对乙容器底部的压强p水。
(3)将甲浸没在乙容器的水中,容器对桌面的压强P2为3000Pa,通过计算说明容器中的水有无溢出。
四、液面变化问题
如图所示,金属圆柱体甲的高度为0.1米,底面积为1×10-2m2;薄壁圆柱形容器乙的底面积为2×10-2m2,且足够高,其中盛有深度为0.15m的水,置于水平面上。
(1)求水对乙容器底部的压强p水。(g取9.8N/kg)(2)现将甲浸入乙容器的水中,当甲的下表面从刚好与水面接触开始向下移动0.04米。(a)求甲浸入水中的体积V浸。(b)求水对乙容器底部压力的增加量ΔF。
答案:(1)1470Pa;(2 a)8×10-4m3;(2 b) 7.84N。
四、液面变化问题(能力提升)
【例题】如图所示装置中,不吸水的正方体A和B通过轻质细线连接悬挂于天花板上,水平桌面上有一足够高的柱形容器重为4N、底面积为200cm2。已GA=3N,GB=17N,A和B的边长、连接A和B的细线长以及B的下表面到容器底的距离均为10cm。现向容器中韩漫加入水,当加入5kg的水时水对容器底部的压强是______Pa;然后剪断A上方的细线,待A、B静止后,容器对水平桌面的压强变化量是______Pa。
3000
500
解析:
解析
五、与叠放相结合
【例题】如图所示,A和B是密度为2.5×10 kg/m 的材料制作的两块形状完全相同的实心长方体砖,分别侧放和平放在水平桌面上。B砖上放有质量忽略不计的薄壁圆柱形容器,容器中盛有部分酒精(ρ酒精 = 0.8×10 kg/m ),容器底面积为B砖上表面积的四分之一、A砖的上表面和B砖的上表面到水平桌面的距离分别为20 cm和4 cm,将A砖沿竖直方向切去一半后剩余部分对水平桌面的压强为_________Pa;若切割后的A砖对水平桌面的压强为B砖对水平桌面的压强的四倍,则容器中酒精的深度为________cm。
六、与切割相结合
【例题】如图所示,质量为2kg,边长为0.1m均匀正方体甲和底面积为0.04m2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1m深的水。
(1)求正方体甲的密度;
(2)求水对乙容器底部的压强;
(3)现将甲物体水平或竖直切去一部分,并将切去部分浸入水中,其中能使正方体甲对地面的压强等于水对乙容器底部的压强的是________(选填“水平切”或“竖直切”);请通过计算算出切去部分的质量。(g=10N / kg )
2×103kg/m3
1000Pa
水平切、0.89kg
解析
七、连通器、帕斯卡定律的运用
【例题】如图所示,左右两柱形玻璃管形状、大小均相同,分别注入水和煤油,放在水平桌面上。水和煤油对玻璃管底部的压强相等。两管距离底部相同高度的地方通过水平细管相连,细管中的阀门位于水平管中央,将水和煤油隔离,两管中的液面水平。当阀门打开瞬间,细管中的液体( )
A.向左流动 B.向右流动
C.不动 D.水向右流动,煤油向左流动
A
【例题】智慧的劳动人民在劳动中创造了液压机,如图所示的简易液压机的活塞A、B的面积为SA=10cm2,SB=200cm2。把重力为630N的物体放在活塞B上,则以下结论正确的是( )
A.活塞B将向下移动15cm B.活塞B将向下移动15.75cm
C.活塞B将向下移动14.25cm D.活塞B将向下移动任意距离
七、连通器、帕斯卡定律的运用
A
第九章:压强
液体的压强 习题课
初中物理人教版
物理
知识回顾
1.液体压强的计算公式:
2.液体对容器底部的压力的三种情况(均为G液)
G液=F底
G液>F底
G液
【例题】装有一定量水的细玻璃管斜放在水平桌面上,如图所示,则此时水对玻璃管底部的压强为(g取10N/kg,ρ水=1.0×103kg/m3)( )
A.8×102Pa B.1×103Pa C.8×104Pa D.1×105Pa
【例题】如图,甲、乙两支完全相同的试管,装有质量相同的不同种液体,甲管竖直,乙管倾斜,此时两管内的液面相平,则两支试管的底部受到液体的压强关系正确的是( )
A.p甲>p乙 B.p甲=p乙 C.p甲
A
一、液体压强计算公式的运用
【例题】如图甲所示,密闭的容器重为20N,底面积为100cm2,其中装有8kg的水,水的深度为15cm,平放在面积为1m2的水平台面上。桶底受到水的压力为____N;水对桶底的压强为______Pa;台面受到桶的压力为______N;台面受到桶的压强为______Pa,若把该容器倒放在该桌面上,如图乙所示,那么水对容器底的压强将______,压力将______,容器对桌面的压强将______,压力将______。(均选填“变大”、“变小”或“不变”)(ρ水=1×103kg/m3,g取10N/kg)
15
1500
100
1×104
变小
变大
变小
不变
一、液体压强计算公式的运用(升级)
【例题】轻质圆柱形容器A、B放在水平桌面上,盛有质量相同的不同液体,两容器中液体的液面高度相同,如图所示,现有质量相同的甲、乙两实心球(ρ甲>ρ乙)。选择其中一球放入某容器中,球浸没且液体不溢出,要使液体对容器底部的压强p最大,则( )
A.甲放入A中 B.甲放入B中C.乙放入A中 D.乙放入B中
C
一、液体压强计算公式的运用(升级)
【例题】如图所示,甲、乙两个相同的轻质薄壁圆柱形容器(高为1m,底面积为5×10-2m2)放置在水平地面上,且容器内分别盛有深度都为0.8m的水和酒精(酒精密度0.8×103kg/m3)。
g=10N/kg。求(1)求甲容器中水的质量m水。(2)求酒精对容器乙底部的压强p酒精。(3)现将密度为ρ的实心物体A先后慢慢放入水和酒精中,发现两容器都有液体溢出,当物体A静止后,甲、乙容器对地面的压强增加量相同,且溢出酒精的体积为10×10-3m3。求溢出水与溢出酒精的体积之比。
40kg
6400Pa
4:5
【例题】甲乙两个相同的容器分别装有质量相等的酒精和水,设容器底部受到水和酒精的压强分别为p甲和p乙,容器底部受到水和酒精的压力分别为F甲和F乙,则下列选项中正确的是( )
A.p甲>p乙 F甲<F乙 B.p甲<p乙 F甲<F乙C.p甲>p乙 F甲>F乙 D.p甲<p乙 F甲=F乙
一、液体压强计算公式的运用(升级)割补法
这样子的,我们可以理解成这个容器是柱体部分和凸出去的两部分之和,而凸出去的是对左右的压强,没有到容器底部,柱体的全部传到容器底部了
B
一、液体压强计算公式的运用(升级)割补法
【例题】在两个完全相同的容器中分别倒入甲和乙两种不同的液体,如图所示,下列分析正确的是( )
A.若甲和乙的质量相等,则甲的密度小于乙的密度B.若甲和乙对容器底部的压强相等,则甲的密度小于乙的密度C.若甲和乙对容器底部的压强相等,则甲的质量小于乙的质量D.若甲和乙的质量相等,则甲对容器底部的压强小于乙对容器底部的压强
①
⑤
⑥
④
②
③
C
解析的等效图
用基本公式法的时候,要注意:有时候整体代换很重要
二、抽倒液体
【例题】如图所示,底面积不同的薄壁圆柱形容器A和B分别盛有甲、乙两种液体,两液面保持相平。现从两容器中抽出部分液体后,其液面仍保持相平,若此时甲对A底部的压力大于乙对B底部的压力,则抽取前,甲、乙各自对容器底部的压强pA、pB和压力FA、FB的关系是( )
A.pA<pB,FA<FB B. pA<pB,FA>FBC. pA>pB,FA<FB D. pA>pB,FA>FB
二、抽倒液体
D
二、抽倒液体
【例题】底面积不同的圆柱形容器A和B原先分别盛有体积相同的甲、乙两种液体,如图所示,现从容器中分别抽出部分液体后,液体对各自容器底部的压强为p甲、p乙,则下列做法中,符合实际的是( )
A.若液体原先对容器底部的压力相等,则抽出相等质量的液体后,p甲一定等于p乙B.若液体原先对容器底部的压力相等,则抽出相等厚度的液体后,p甲可能大于p乙C.若液体原先对容器底部的压强相等,则抽出相等体积的液体后,p甲一定等于p乙D.若液体原先对容器底部的压强相等,则抽出相等厚度的液体后,p甲一定等于p乙
C
【例题】如图所示,两薄壁圆柱形容器内分别盛有甲、乙两种液体放置在水平地面上,现从两容器中分别抽出部分液体,使甲、乙剩余部分的深度均为h,若此时两液体对容器底部的压力相等;则甲、乙抽出部分的质量m甲、m乙及液体对容器底部压强变化p甲、p乙的大小关系是( )
A.m甲<m乙, p甲>p乙 B.m甲>m乙, p甲>p乙C.m甲=m乙, p甲<p乙 D.m甲<m乙, p甲<p乙
二、抽倒液体
D
二、抽倒液体
【例题】如图所示,底面积不同的圆柱形容器分别盛有甲、乙两种液体,液体对各自容器底部的压力相等。现分别从两容器中抽出液体,且剩余液体的液面到容器底部的距离均为h,则剩余液体对各自容器底部的压强p、压力F的关系是( )
A.p甲
C.p甲>p乙;F甲> F乙 D.p甲
二、抽倒液体
【例题】如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有水和酒精(ρ水>ρ酒精),且两种液体对容器底部的压强相等。一定能使水对容器底部的压强大于酒精对容器底部压强的方法是( )
A.倒入相同质量的水和酒精 B.倒入相同体积的水和酒C.抽出相同质量的水和酒精 D.抽出相同体积的水和酒精
C
C
二、抽倒液体(能力提升)
【例题】如图所示,A、B 两个柱形容器(SA>SB,容器足够高),分别盛有质量相同的甲、乙两种液体,则下列说法正确的是( )
A.分别向A、B 容器中倒入相同质量的甲、乙液体后,液体对容器底部的压强 p 甲可能等于 p 乙B.分别从A、B 容器中抽出相同体积的甲、乙液体后,液体对容器底部的压强 p 甲一定大于 p 乙C.分别向A、B 容器中倒入相同高度的甲、乙液体后,液体对容器底部的压力 F 甲一定小于 F 乙D.分别从A、B 容器中抽出相同高度的甲、乙液体后,液体对容器底部的压强 p 甲一定大于 p 乙
【例题】如图所示,往装有水的容器内匀速下插一长方体物体(未触底),容器中水面逐渐上升,容器底面受到水的压强p随时间t变化的曲线,较合理的是( )
三、图像问题
C
【例题】如图甲所示的容器放置在水平地面上,该容器上、下两部分都是圆柱形,其横截面积分别为S1、S2,容器底部装有控制阀门。容器内装有密度为0.8×103kg/m3的液体,液体通过控制阀门匀速排出的过程中,容器底部受到液体的压强P随时间t变化关系如图乙所示。则阀门打开前液体的深度H=_______cm,上、下两部分横截面积之比S1:S2=_______。(g取10N/kg)
三、图像问题
15
1:4
【例题】如图,实心圆柱体甲、乙的密度均为3×103 kg/m3,甲的质量为6 kg,底面积为200 cm2;乙的质量为12kg,底面积为300 cm2。水平地面上的轻质薄壁容器丙内盛有9 cm深的水,容器上部分高度为下部分高度的五分之一,容器下底面积为1000 cm2。若把甲沿水平方向切割的高度,切割下来的部分竖直缓慢浸没在丙容器的水中,液面的上升高度与切割的高度的部分关系如图丁所示(g=10N/kg)。求:
(1)圆柱体甲的体积V甲;
(2)容器丙中水的重力;
(3)若将圆柱体乙放入原装有9 cm深水的容器丙中,此时容器丙对水平地面的压强。
三、图像问题(能力提升)
2000cm3
90N
1940Pa
解析
解析
四、液面变化问题
【例题】如图所示,圆柱体甲和轻质薄壁圆柱形容器乙置于水平地面。甲的质量为4kg,乙容器的底面积为2×10-2m2,内有0.2m深的水。(g取10N / kg )
(1)求甲对地面的压力F甲。
(2)求水对乙容器底部的压强p水。
(3)将甲浸没在乙容器的水中,容器对桌面的压强P2为3000Pa,通过计算说明容器中的水有无溢出。
四、液面变化问题
如图所示,金属圆柱体甲的高度为0.1米,底面积为1×10-2m2;薄壁圆柱形容器乙的底面积为2×10-2m2,且足够高,其中盛有深度为0.15m的水,置于水平面上。
(1)求水对乙容器底部的压强p水。(g取9.8N/kg)(2)现将甲浸入乙容器的水中,当甲的下表面从刚好与水面接触开始向下移动0.04米。(a)求甲浸入水中的体积V浸。(b)求水对乙容器底部压力的增加量ΔF。
答案:(1)1470Pa;(2 a)8×10-4m3;(2 b) 7.84N。
四、液面变化问题(能力提升)
【例题】如图所示装置中,不吸水的正方体A和B通过轻质细线连接悬挂于天花板上,水平桌面上有一足够高的柱形容器重为4N、底面积为200cm2。已GA=3N,GB=17N,A和B的边长、连接A和B的细线长以及B的下表面到容器底的距离均为10cm。现向容器中韩漫加入水,当加入5kg的水时水对容器底部的压强是______Pa;然后剪断A上方的细线,待A、B静止后,容器对水平桌面的压强变化量是______Pa。
3000
500
解析:
解析
五、与叠放相结合
【例题】如图所示,A和B是密度为2.5×10 kg/m 的材料制作的两块形状完全相同的实心长方体砖,分别侧放和平放在水平桌面上。B砖上放有质量忽略不计的薄壁圆柱形容器,容器中盛有部分酒精(ρ酒精 = 0.8×10 kg/m ),容器底面积为B砖上表面积的四分之一、A砖的上表面和B砖的上表面到水平桌面的距离分别为20 cm和4 cm,将A砖沿竖直方向切去一半后剩余部分对水平桌面的压强为_________Pa;若切割后的A砖对水平桌面的压强为B砖对水平桌面的压强的四倍,则容器中酒精的深度为________cm。
六、与切割相结合
【例题】如图所示,质量为2kg,边长为0.1m均匀正方体甲和底面积为0.04m2的薄壁柱形容器乙放在水平地面上,乙容器足够高,内盛有0.1m深的水。
(1)求正方体甲的密度;
(2)求水对乙容器底部的压强;
(3)现将甲物体水平或竖直切去一部分,并将切去部分浸入水中,其中能使正方体甲对地面的压强等于水对乙容器底部的压强的是________(选填“水平切”或“竖直切”);请通过计算算出切去部分的质量。(g=10N / kg )
2×103kg/m3
1000Pa
水平切、0.89kg
解析
七、连通器、帕斯卡定律的运用
【例题】如图所示,左右两柱形玻璃管形状、大小均相同,分别注入水和煤油,放在水平桌面上。水和煤油对玻璃管底部的压强相等。两管距离底部相同高度的地方通过水平细管相连,细管中的阀门位于水平管中央,将水和煤油隔离,两管中的液面水平。当阀门打开瞬间,细管中的液体( )
A.向左流动 B.向右流动
C.不动 D.水向右流动,煤油向左流动
A
【例题】智慧的劳动人民在劳动中创造了液压机,如图所示的简易液压机的活塞A、B的面积为SA=10cm2,SB=200cm2。把重力为630N的物体放在活塞B上,则以下结论正确的是( )
A.活塞B将向下移动15cm B.活塞B将向下移动15.75cm
C.活塞B将向下移动14.25cm D.活塞B将向下移动任意距离
七、连通器、帕斯卡定律的运用
A
