2022-2023学年北师大版八年级数学下册1.4 角平分线 同步练习(无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册1.4 角平分线 同步练习(无答案) | 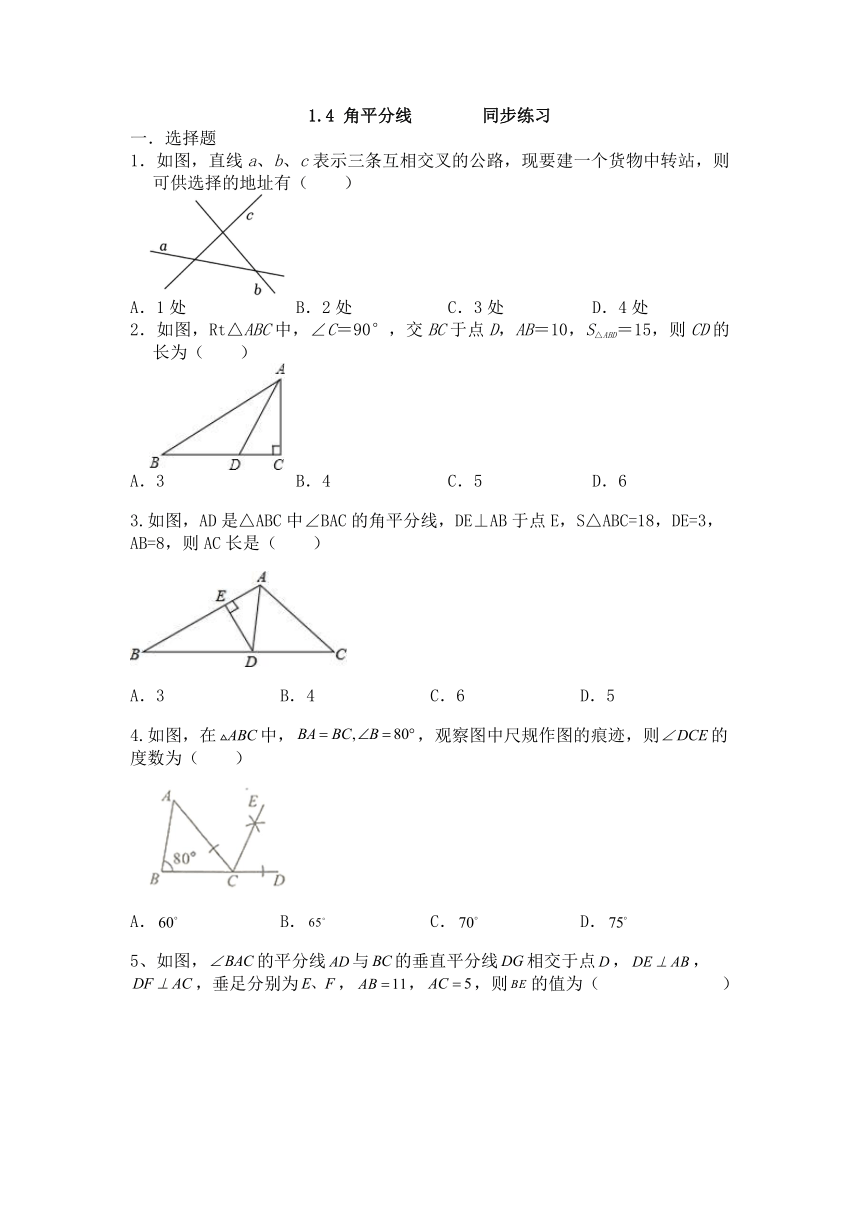 | |
| 格式 | docx | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 19:07:09 | ||
图片预览


文档简介
1.4 角平分线 同步练习
一.选择题
1.如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
2.如图,Rt△ABC中,∠C=90°,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
3.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=18,DE=3,AB=8,则AC长是( )
A.3 B.4 C.6 D.5
4.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
5、如图,的平分线与的垂直平分线相交于点,,,垂足分别为,,,则的值为( )
A.1 B. C.2 D.3
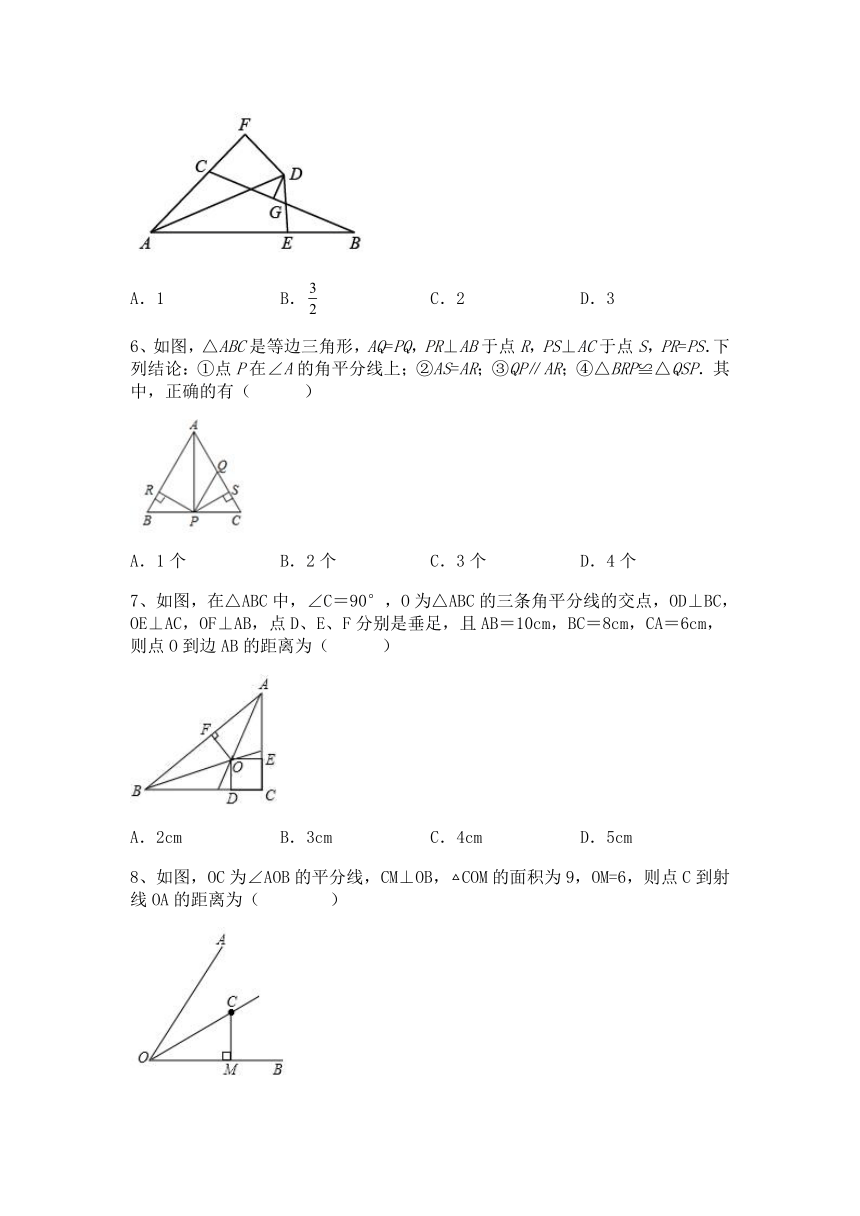
6、如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
7、如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
8、如图,OC为∠AOB的平分线,CM⊥OB,COM的面积为9,OM=6,则点C到射线OA的距离为( )
A.9 B.6 C.3 D.4.5
9.如图,在△ABC中,AB>AC,AD是△ABC的角平分线,点E在AC上,过点E作EF⊥BC于点F,延长CB至点G,使BG=2FC,连接EG交AB于点H,EP平分∠GEC,交AD的延长线于点P,连接PH,PB,PG,若∠C=∠EGC+∠BAC,则下列结论:①∠APE=1/2∠AHE;②PE=HE;③AB=GE;④S△PAB=S△PGE.其中正确的有( )
A.①②③ B.①②③④ C.①② D.①③④
10.如图,Rt△ACB中,∠ACB=90°,△ACB的角平分线AD,BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°; ②AD=PF+PH;③DH平分∠CDE;④S四边形ABDE=S△ABP;⑤S△APH=S△ADE,其中正确的结论有( )个
A.2 B.3 C.4 D.5
二、填空题。
1.如图,OC是∠AOB的平分线,点P是OC上一点,PM⊥OB于点M,点N是射线OA上一动点,若PM=7,则PN的最小值为 。
2.如图,在中,,为的角平分线,且于D,若,则的长为_________.
3.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,以下五个结论:①AD=BE;②PQ//AE;③连接CO,则OC平分∠AOE;④DE=DP;⑤△CPQ为等边三角形.恒成立的结论有___________________(把你认为正确的序号都填上).
4.如图,在Rt△ABC中,∠B=90°,以顶点C为圆心、适当长为半径画弧,分别交AC、BC于点E、F,再分别以点E、F为圆心,以大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=4,AC=16,则△ACD的面积是______.
5、如图,为的平分线.,..则点到射线的距离为__________.
6、如图,是等边的角平分线,,垂足为点,线段的垂直平分线交于点,垂足为,若,则的长为__________.
三.解答题
1.如图,在Rt△ABC中,∠ACB=90°,DE⊥AB,垂足为D,AB=10,
(1)求DE的长度.
(2)求△ABE的面积.
2.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:PE=PF;
3、如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
4.已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.
(1)求证:△ABD≌△ACE;
(2)求证:FA平分∠BFE.
5、在Rt△ABC中,,AE是斜边BC上的高,角平分线BD交AE于点G,交AC于点D,于点F.
(1)求证:;
(2)试判断AD与AG有怎样的数量关系?请说明理由.
一.选择题
1.如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
2.如图,Rt△ABC中,∠C=90°,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
3.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=18,DE=3,AB=8,则AC长是( )
A.3 B.4 C.6 D.5
4.如图,在中,,观察图中尺规作图的痕迹,则的度数为( )
A. B. C. D.
5、如图,的平分线与的垂直平分线相交于点,,,垂足分别为,,,则的值为( )
A.1 B. C.2 D.3
6、如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
7、如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
8、如图,OC为∠AOB的平分线,CM⊥OB,COM的面积为9,OM=6,则点C到射线OA的距离为( )
A.9 B.6 C.3 D.4.5
9.如图,在△ABC中,AB>AC,AD是△ABC的角平分线,点E在AC上,过点E作EF⊥BC于点F,延长CB至点G,使BG=2FC,连接EG交AB于点H,EP平分∠GEC,交AD的延长线于点P,连接PH,PB,PG,若∠C=∠EGC+∠BAC,则下列结论:①∠APE=1/2∠AHE;②PE=HE;③AB=GE;④S△PAB=S△PGE.其中正确的有( )
A.①②③ B.①②③④ C.①② D.①③④
10.如图,Rt△ACB中,∠ACB=90°,△ACB的角平分线AD,BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°; ②AD=PF+PH;③DH平分∠CDE;④S四边形ABDE=S△ABP;⑤S△APH=S△ADE,其中正确的结论有( )个
A.2 B.3 C.4 D.5
二、填空题。
1.如图,OC是∠AOB的平分线,点P是OC上一点,PM⊥OB于点M,点N是射线OA上一动点,若PM=7,则PN的最小值为 。
2.如图,在中,,为的角平分线,且于D,若,则的长为_________.
3.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,以下五个结论:①AD=BE;②PQ//AE;③连接CO,则OC平分∠AOE;④DE=DP;⑤△CPQ为等边三角形.恒成立的结论有___________________(把你认为正确的序号都填上).
4.如图,在Rt△ABC中,∠B=90°,以顶点C为圆心、适当长为半径画弧,分别交AC、BC于点E、F,再分别以点E、F为圆心,以大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=4,AC=16,则△ACD的面积是______.
5、如图,为的平分线.,..则点到射线的距离为__________.
6、如图,是等边的角平分线,,垂足为点,线段的垂直平分线交于点,垂足为,若,则的长为__________.
三.解答题
1.如图,在Rt△ABC中,∠ACB=90°,DE⊥AB,垂足为D,AB=10,
(1)求DE的长度.
(2)求△ABE的面积.
2.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:PE=PF;
3、如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
4.已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.
(1)求证:△ABD≌△ACE;
(2)求证:FA平分∠BFE.
5、在Rt△ABC中,,AE是斜边BC上的高,角平分线BD交AE于点G,交AC于点D,于点F.
(1)求证:;
(2)试判断AD与AG有怎样的数量关系?请说明理由.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
