六年级下册数学课件-第二单元《比例》单元整理和复习北师大版(共27张PPT)
文档属性
| 名称 | 六年级下册数学课件-第二单元《比例》单元整理和复习北师大版(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 08:30:54 | ||
图片预览








文档简介
(共27张PPT)
比例的整理和复习
2
重点知识归纳
比例的意义
比例的基本性质
正比例和反比例的意义
比例尺
图形的放大与缩小
用比例解决问题
基本知识点
1、比例的意义
表示两个比相等的式子
在比例里,两个外项的积等于两个内项的积
2、比例的基本性质
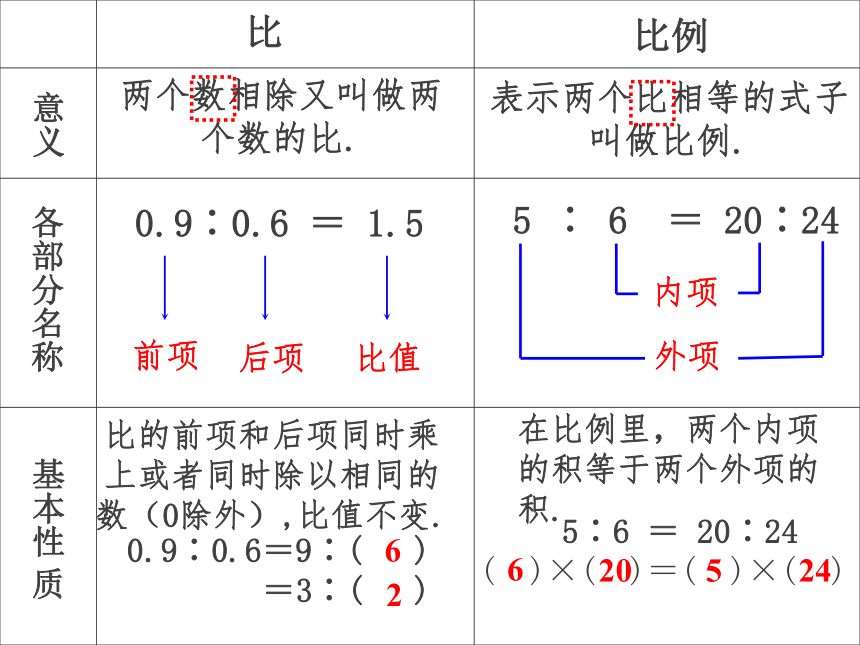
比
比例
意义
各部分名称
基本性 质
两个数相除又叫做两
个数的比.
表示两个比相等的式子
叫做比例.
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
0.9∶0.6=9∶( )
=3∶( )
6
2
在比例里,两个内项的积等于两个外项的积.
5∶6 = 20∶24
( )×( )=( )×( )
6
20
5
24
利用你喜欢的方法判断下列哪组中的两个比是否可以组成比例,并把它写出来。
6:3和8:5 0.2:2.5和4:50
—:—和—:— 1.4:2和7:10
2
1
5
1
8
5
4
1
可以利用求比值和比例的基本性质 (假设法)来判断两个比是否可以组成比例。
练一练
1、解下列比例
0.25:x=15:100 — =- -:x=0.3:0.5
0.2
1.5
0.4
x
5
2
-
100
2.5x
=
-
2
2-0.9
1-:x=0.5:16
8
综合练习
填空:
1)一个比例有两个( )项,两个( )项。
2)判断两个比是否能组成比例,可以看它们的( )也可以用( ) 进行判断。
3)写出比值是2.5的比,并组成比例( )
4)在比例中,如果两个内项的分别是4和5,那么组成
两个外项的两个数的积一定是( )
内
外
5:2=10:4
20
5
比值
比例基本性质
5)甲数是乙数的1-,甲数和乙数的比是( ),比值是( )。
6)( )成= — =( )÷20=0.8=( )℅=( 48 ):60
7)甲数和乙数的比是3:5,甲数占乙数的-,乙数占甲乙两数总数的-。
8)3x=4y,(x、y都不为0),x和 y的比是( ):( )
9)两个数的比值是4,前项和后项同时扩大3倍,比值是( )。
2
1
( )
20
2、选择
3:2
1.5
25
16
80
3
5
8
5
4
3
不变
8
1)两和正方形的边长的比是3:5,它们面积的比是( ),周长的比是( )。
A:1:3 B: 3:5 C:1:25 D:9:25
2)把100克白糖放如1000克水中,糖和水的比是( )
a: 1:12 b: 1:11 c : 1:10 d: 1:9
3)比的前项扩大2倍,后项缩小2倍,比值( )
a: 扩大4倍 b: 缩小4倍 c:不变 d: 扩大2倍
4)甲数的-等于乙数的- ,乙数与甲数的比是( )
A : 25:18 b: 18:25 c: 1:2 d: 2:1
5)一个圆柱和圆锥等高等体积,他们的底面积的比是( ) 。
5
3
6
5
D
B
C
a
A
a
a: 1:3 b: 3:1 c: 1: 9 d: 9:1
3、判断:
1)正方形的面积的比等于边长的比( )
2)如果a:b的比是3:4,3a =4b。( )
3)45分:1-时的比值是0.6。( )
4)-化简后是最简整数比是2-。( )
4
1
4
10
2
1
4、根据要求写出一个比例式
1)两个外项分别是3和x,两和内项分别是9和12。
2)等号左边的比是x:5,右边比的比值是5。
3)使各项都是整数,且两个比的比值为0.8。
×
×
×
×
说说正比例和反比例的意义。
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的比值(也就是商)一定,
这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的积一定,
这两种量就叫做成反比例的量,
它们的关系叫做反比例关系。
正比例和反比例有什么联系和区别?
正比例 反比例
共同点 不同点
1.都有两种相关联的量;
2.一种量随着另一种量变化而变化
1.一种量扩大或缩小,另一种量也扩大或缩小。(变化方向相同)
2.相对应的两个数的比值(商)是一定的。
Y/X=K(一定)
1.一种量扩大或缩小,另一种量反而缩小或扩大。(变化方向相反)
2.相对应的两个数的积是一定的。
XY=K(一定)
练习3:
判断下面各题中两种量成什么比例:
1、工作总量一定,工作效率和工作时间。
2、A=8B,A和B。
3、平行四边形的底一定,面积和高。
4、长方形的面积一定,长和宽。
反比例
正比例
正比例
反比例
3、比例尺
图上距离∶实际距离 = 比例尺
图上距离
实际距离
= 比例尺
(1)数值比例尺
(2) 线段比例尺
或:
0
10
20千米
0
70
140千米
0
200
400 米
表示地图上1厘米距离
相当于地面上10千米距离
表示地图上1厘米距离
相当于地面上200米距离
表示地图上1厘米距离
相当于地面上70千米距离
第一、梳理相关联的两种量。
第二、判断相关联的两种量成什么比例,
写出关系式。
第三、写“解”,设未知数。
第四、按两种相关联的量所成的比例关系
列出比例式。
第五、解比例。
第六、用自己熟练的方法检验结果是否正
确是否符合题意。
第七、作答。
5、说一说用比例解决问题的步骤:
练习1:
甲乙两地相距2千米,画在一幅
图上的距离是5厘米,求这幅图
的比例尺。
练习2: 比例的应用
应用比例来解决一些实际问题
1、小红8分钟走了500米,照这样的速度,她从家里走到学校用了14分钟,小红家离学校大约多少米
解:设小红家离学校有x米。
=500×14
=500×14÷8
=875
答:小红家离学校有875米。
3、在太阳的照射下,测得某身高为1.75米人的影子长1米长,然后又测得某电线杆的影子长8米,问能求出电线杆的高吗?
想一想下面两种量成什么比例关系?
1、正方体的棱长和体积。
2、车轮的周长一定,车轮的转数
和所行驶的路程。
练习2:
在地图上量的两城的距离是8厘米,已知这幅图的比例尺是1∶120 0000,两城的实际距离是多少千米?
2、一种糖水,糖和水按照1∶150配制的;现有糖100克,可以配制这样的糖水多少克?
解:设需要 克水来配制这样的糖水。
1∶150=100∶
1× =150×100
=15000
15000+100=15100(克)
答:可以配置这样的糖水15100克
3、一支工程队铺一段铁路,原计划每天铺
3.2千米,实际每天比原计划多铺25%,
实际铺完这段铁路用了12天。原计划用
多少天才能铺完?
解:设原计划用X天才能铺完。
3.2× X=3.2×(1+25%) ×12
3.2X=4×12
X=15
答:原计划用15天才能铺完。
4、用同样的砖铺地,铺15平方米要用600块砖。如果铺20平方米,要用多少块砖?
5.(1)一间房子要用方砖铺地。用面积是9平方分米的方砖,需要96块。如果改用面积是4平方分米的方砖,需要多少块?
(2)一间房子要用方砖铺地。用边长是3分米的方砖,需要96块。如果改用边长是2分米的方砖,需要多少块?
比一比:以上两题有什么相同和不同?
想:铺地面积一定,地砖块数与地砖( )成( )比例
4X=9x96
(2x2)X=(3x3)x96
面积
反
比
例
意义
:
( 求比例中的未知项叫做解比例)。
图上距离与实际距离的比,叫做比例尺。
基本性质
分类
应用
概念
应用
:
:
在比例里,两个外项的积等于两个内项的积,叫做比例的基本性质。
解比例
正比例 :
反比例 :
比例尺
:
图形的变换(放大与缩小)
用正 反比例解决问题
、
y
x
=
k
(一定)
X × y=k(一定)
表表示两个比相等的式子叫做比例。
比例的整理和复习
2
重点知识归纳
比例的意义
比例的基本性质
正比例和反比例的意义
比例尺
图形的放大与缩小
用比例解决问题
基本知识点
1、比例的意义
表示两个比相等的式子
在比例里,两个外项的积等于两个内项的积
2、比例的基本性质
比
比例
意义
各部分名称
基本性 质
两个数相除又叫做两
个数的比.
表示两个比相等的式子
叫做比例.
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
0.9∶0.6=9∶( )
=3∶( )
6
2
在比例里,两个内项的积等于两个外项的积.
5∶6 = 20∶24
( )×( )=( )×( )
6
20
5
24
利用你喜欢的方法判断下列哪组中的两个比是否可以组成比例,并把它写出来。
6:3和8:5 0.2:2.5和4:50
—:—和—:— 1.4:2和7:10
2
1
5
1
8
5
4
1
可以利用求比值和比例的基本性质 (假设法)来判断两个比是否可以组成比例。
练一练
1、解下列比例
0.25:x=15:100 — =- -:x=0.3:0.5
0.2
1.5
0.4
x
5
2
-
100
2.5x
=
-
2
2-0.9
1-:x=0.5:16
8
综合练习
填空:
1)一个比例有两个( )项,两个( )项。
2)判断两个比是否能组成比例,可以看它们的( )也可以用( ) 进行判断。
3)写出比值是2.5的比,并组成比例( )
4)在比例中,如果两个内项的分别是4和5,那么组成
两个外项的两个数的积一定是( )
内
外
5:2=10:4
20
5
比值
比例基本性质
5)甲数是乙数的1-,甲数和乙数的比是( ),比值是( )。
6)( )成= — =( )÷20=0.8=( )℅=( 48 ):60
7)甲数和乙数的比是3:5,甲数占乙数的-,乙数占甲乙两数总数的-。
8)3x=4y,(x、y都不为0),x和 y的比是( ):( )
9)两个数的比值是4,前项和后项同时扩大3倍,比值是( )。
2
1
( )
20
2、选择
3:2
1.5
25
16
80
3
5
8
5
4
3
不变
8
1)两和正方形的边长的比是3:5,它们面积的比是( ),周长的比是( )。
A:1:3 B: 3:5 C:1:25 D:9:25
2)把100克白糖放如1000克水中,糖和水的比是( )
a: 1:12 b: 1:11 c : 1:10 d: 1:9
3)比的前项扩大2倍,后项缩小2倍,比值( )
a: 扩大4倍 b: 缩小4倍 c:不变 d: 扩大2倍
4)甲数的-等于乙数的- ,乙数与甲数的比是( )
A : 25:18 b: 18:25 c: 1:2 d: 2:1
5)一个圆柱和圆锥等高等体积,他们的底面积的比是( ) 。
5
3
6
5
D
B
C
a
A
a
a: 1:3 b: 3:1 c: 1: 9 d: 9:1
3、判断:
1)正方形的面积的比等于边长的比( )
2)如果a:b的比是3:4,3a =4b。( )
3)45分:1-时的比值是0.6。( )
4)-化简后是最简整数比是2-。( )
4
1
4
10
2
1
4、根据要求写出一个比例式
1)两个外项分别是3和x,两和内项分别是9和12。
2)等号左边的比是x:5,右边比的比值是5。
3)使各项都是整数,且两个比的比值为0.8。
×
×
×
×
说说正比例和反比例的意义。
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的比值(也就是商)一定,
这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
两种相关联的量,
一种量变化,另一种量也随着变化。
如果这两种量中相对应的两个数的积一定,
这两种量就叫做成反比例的量,
它们的关系叫做反比例关系。
正比例和反比例有什么联系和区别?
正比例 反比例
共同点 不同点
1.都有两种相关联的量;
2.一种量随着另一种量变化而变化
1.一种量扩大或缩小,另一种量也扩大或缩小。(变化方向相同)
2.相对应的两个数的比值(商)是一定的。
Y/X=K(一定)
1.一种量扩大或缩小,另一种量反而缩小或扩大。(变化方向相反)
2.相对应的两个数的积是一定的。
XY=K(一定)
练习3:
判断下面各题中两种量成什么比例:
1、工作总量一定,工作效率和工作时间。
2、A=8B,A和B。
3、平行四边形的底一定,面积和高。
4、长方形的面积一定,长和宽。
反比例
正比例
正比例
反比例
3、比例尺
图上距离∶实际距离 = 比例尺
图上距离
实际距离
= 比例尺
(1)数值比例尺
(2) 线段比例尺
或:
0
10
20千米
0
70
140千米
0
200
400 米
表示地图上1厘米距离
相当于地面上10千米距离
表示地图上1厘米距离
相当于地面上200米距离
表示地图上1厘米距离
相当于地面上70千米距离
第一、梳理相关联的两种量。
第二、判断相关联的两种量成什么比例,
写出关系式。
第三、写“解”,设未知数。
第四、按两种相关联的量所成的比例关系
列出比例式。
第五、解比例。
第六、用自己熟练的方法检验结果是否正
确是否符合题意。
第七、作答。
5、说一说用比例解决问题的步骤:
练习1:
甲乙两地相距2千米,画在一幅
图上的距离是5厘米,求这幅图
的比例尺。
练习2: 比例的应用
应用比例来解决一些实际问题
1、小红8分钟走了500米,照这样的速度,她从家里走到学校用了14分钟,小红家离学校大约多少米
解:设小红家离学校有x米。
=500×14
=500×14÷8
=875
答:小红家离学校有875米。
3、在太阳的照射下,测得某身高为1.75米人的影子长1米长,然后又测得某电线杆的影子长8米,问能求出电线杆的高吗?
想一想下面两种量成什么比例关系?
1、正方体的棱长和体积。
2、车轮的周长一定,车轮的转数
和所行驶的路程。
练习2:
在地图上量的两城的距离是8厘米,已知这幅图的比例尺是1∶120 0000,两城的实际距离是多少千米?
2、一种糖水,糖和水按照1∶150配制的;现有糖100克,可以配制这样的糖水多少克?
解:设需要 克水来配制这样的糖水。
1∶150=100∶
1× =150×100
=15000
15000+100=15100(克)
答:可以配置这样的糖水15100克
3、一支工程队铺一段铁路,原计划每天铺
3.2千米,实际每天比原计划多铺25%,
实际铺完这段铁路用了12天。原计划用
多少天才能铺完?
解:设原计划用X天才能铺完。
3.2× X=3.2×(1+25%) ×12
3.2X=4×12
X=15
答:原计划用15天才能铺完。
4、用同样的砖铺地,铺15平方米要用600块砖。如果铺20平方米,要用多少块砖?
5.(1)一间房子要用方砖铺地。用面积是9平方分米的方砖,需要96块。如果改用面积是4平方分米的方砖,需要多少块?
(2)一间房子要用方砖铺地。用边长是3分米的方砖,需要96块。如果改用边长是2分米的方砖,需要多少块?
比一比:以上两题有什么相同和不同?
想:铺地面积一定,地砖块数与地砖( )成( )比例
4X=9x96
(2x2)X=(3x3)x96
面积
反
比
例
意义
:
( 求比例中的未知项叫做解比例)。
图上距离与实际距离的比,叫做比例尺。
基本性质
分类
应用
概念
应用
:
:
在比例里,两个外项的积等于两个内项的积,叫做比例的基本性质。
解比例
正比例 :
反比例 :
比例尺
:
图形的变换(放大与缩小)
用正 反比例解决问题
、
y
x
=
k
(一定)
X × y=k(一定)
表表示两个比相等的式子叫做比例。
