第一单元圆柱与圆锥常考易错检测卷(单元测试)小学数学六年级下册北师大版(含答案)
文档属性
| 名称 | 第一单元圆柱与圆锥常考易错检测卷(单元测试)小学数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 10:39:46 | ||
图片预览



文档简介
第一单元圆柱与圆锥常考易错检测卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.用铁皮做一个高是5dm,底面直径是4dm的无盖圆柱形水桶,至少需要铁皮( )dm2。
A.263.76 B.87.92 C.62.8 D.75.36
2.贝贝过生日时,收到一个圆锥形陀螺,陀螺的底面直径是6cm,高是5cm。如果把它装在一个圆柱体盒子中,这个盒子的容积至少是( )cm3。
A.125.6 B.141.3 C.150.72 D.226.08
3.一个圆柱和一个圆锥底面半径的比是2∶3,它们的高相等,圆柱和圆锥的体积的最简整数比是( )。
A.9∶4 B.4∶9 C.3∶4 D.4∶3
4.如图,各杯中的饮料,( )。
A.A杯中的最少 B.B杯中的最少 C.C杯中的最少 D.同样多
5.一个圆柱的底面周长是18.84米,高是2米,则这个圆柱的表面积是( )平方米。
A.94.2 B.65.94 C.56.52 D.37.68
6.把一根长20分米的圆柱形木头沿横截面截成5段小圆柱形木头后,表面积比原来增加了80平方分米。这根圆柱形木头的体积是( )立方分米。
A.200 B.180 C.150 D.100
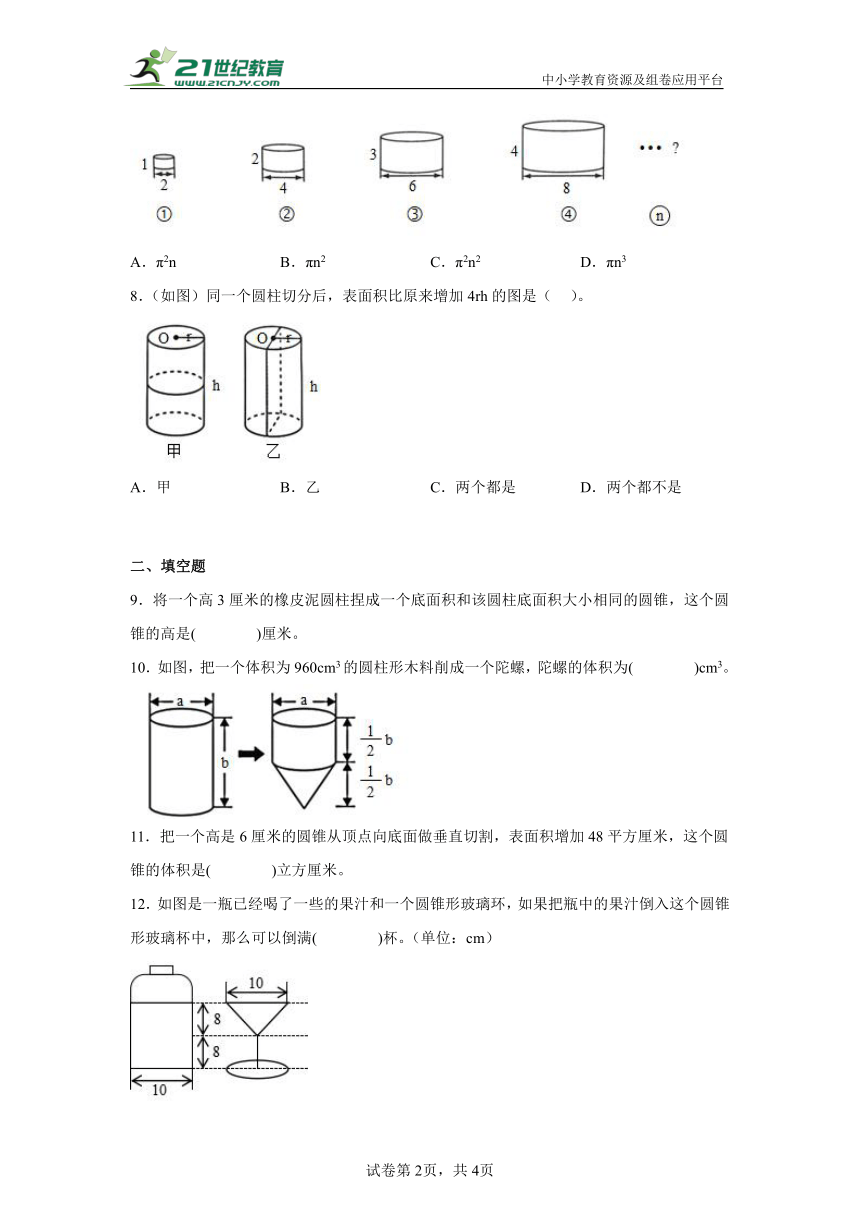
7.观察下面的圆柱,分析它们的底面直径和高的变化引起体积变化的规律,根据这个规律,用含有字母的式子表示第n个圆柱的体积是( )。
A.π2n B.πn2 C.π2n2 D.πn3
8.(如图)同一个圆柱切分后,表面积比原来增加4rh的图是( )。
A.甲 B.乙 C.两个都是 D.两个都不是
二、填空题
9.将一个高3厘米的橡皮泥圆柱捏成一个底面积和该圆柱底面积大小相同的圆锥,这个圆锥的高是( )厘米。
10.如图,把一个体积为960cm3的圆柱形木料削成一个陀螺,陀螺的体积为( )cm3。
11.把一个高是6厘米的圆锥从顶点向底面做垂直切割,表面积增加48平方厘米,这个圆锥的体积是( )立方厘米。
12.如图是一瓶已经喝了一些的果汁和一个圆锥形玻璃环,如果把瓶中的果汁倒入这个圆锥形玻璃杯中,那么可以倒满( )杯。(单位:cm)
13.把一张长12.56分米,宽6.28分米的长方形铁皮圈成一个圆柱铁皮桶,这个铁皮桶的底面积是( )或( )平方分米。(接头处忽略不计)
14.等底等高的圆柱和圆锥,体积差是24立方分米,圆柱的体积是( )立方分米,圆锥的体积是( )立方厘米。
三、判断题
15.有一个圆柱和一个圆锥的底面半径相等,体积也相等,那么圆锥的高是圆柱的高的3倍.( )
16.圆柱的高度不变,底面半径扩大2倍,圆柱的体积也扩大2倍。( )
17.做一个圆柱形玻璃鱼缸,需要多大面积的玻璃需要计算这个圆柱的体积。( )
18.圆柱和圆锥都有1条高。( )
19.一个圆柱的底面半径是r,高是2πr,那么它的侧面沿高展开是正方形。( )
四、图形计算
20.计算(1)的体积,计算(2)的表面积和体积。
(1) (2)
五、解答题
21.妈妈给笑笑的水杯做了一个带底的敞口布套,如图所示。妈妈至少用了多少平方厘米布料?(接头处忽略不计)
22.一个从里面量底面周长是31.4厘米,高是12厘米的圆柱形容器里装有一些水,水中浸没着一个底面半径是3厘米,高是10厘米的圆锥形铁块,如果把圆锥形铁块从水中取出,那么容器中水面高度将下降多少厘米?
23.某公司生产一种饮料,采用圆柱体易拉罐包装,从里面量,底面直径是6厘米,比高少,这个易拉罐最多能装饮料多少毫升?
24.为推进乡村振兴,某乡镇为圆梦社区修建了一个圆柱形水池,从里面量底面直径是8米,池深3米,在水池的底面和内壁涂上水泥,涂水泥部分的面积是多少平方米?
25.一个圆柱形水池,从里面量得它的底面直径是8米,深是2.5米,池上装有3根同样的进水管,每个管每小时可以注入水12.56立方米,三管齐开,几小时可以注满水池?
26.乐乐将一个铁皮油桶在地上滚动一圈,量得其痕迹长12.56分米、宽6分米。制作这个油桶至少需要铁皮多少平方分米?(桶口和盖忽略不计)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】已知这个水桶无盖,所以需要铁皮的面积等于这个圆柱侧面积加上一个底面的面积,根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】3.14×4×5+3.14×(4÷2)2
=12.56×5+3.14×4
=62.8+12.56
=75.36(平方分米)
答:至少需要铁皮75.36平方分米。
故答案为:D
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
2.B
【分析】根据题意可知,圆柱体盒子与圆锥等底等高,根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【详解】3.14×(6÷2)2×5
=3.14×9×5
=28.26×5
=141.3(cm3)
这个盒子的容积至少是141.3cm3。
故答案为:B
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
3.D
【分析】设圆柱的底面半径为2,则圆锥的底面半径为3,高均为h,分别求出圆柱、圆锥的体积,得出体积比并化简即可。
【详解】设圆柱的底面半径为2,则圆锥的底面半径为3,高均为h
圆柱的体积为:π×22×h=4πh
圆锥的体积为:×π×32×h=3πh
圆柱的体积∶圆锥的体积=4πh∶3πh=4∶3。
故答案为:D
【点睛】本题主要考查圆柱、圆锥的体积公式的灵活运用。
4.B
【分析】利用底面积乘饮料的高度即可比较体积大小,据此解答。
【详解】A.3.14×(4÷2)2×2
=3.14×4×2
=25.12(立方厘米)
B.3.14×(2÷2)2×4
=3.14×1×4
=12.56(立方厘米)
C.4×4×2
=16×2
=32(立方厘米)
因为12.56<25.12<32,所以B杯中的饮料最少。
故答案为:B
【点睛】本题考查了长方体、圆柱的体积公式的应用。
5.A
【分析】圆柱的表面积=侧面积+底面积×2,而圆柱的侧面积=底面周长×高。已知圆柱的底面周长,先根据“圆的周长=2πr”求出圆柱的底面半径,再根据“圆的面积=πr2”可以求出圆柱的底面积。分别把数据代入公式求出侧面积和底面积,最后求出圆柱的表面积。
【详解】18.84÷3.14÷2=3(米)
18.84×2+3.14×33×2
=37.68+56.52
=94.2(平方米)
故答案为:A
【点睛】本题考查圆柱的表面积。掌握并熟练运用圆柱的表面积、侧面积以及圆的周长和面积公式是解题的关键。
6.A
【分析】把圆柱形木头沿横截面截成5段小圆柱形木头,要切割4次,表面积比原来增加了4×2=8(个)横截面的面积,据此用80除以8即可求出横截面的面积。圆柱的体积=底面积×高=横截面面积×长,据此解答。
【详解】(5-1)×2=8(个)
80÷8×20
=10×20
=200(立方分米)
故答案为:A
【点睛】本题考查了立体图形的切拼和圆柱的体积。明确“圆柱的表面积比原来增加了8个横截面的面积”,从而求出横截面的面积是解题的关键。
7.D
【分析】根据圆柱体积公式:V=πr2h,依次计算出图①、②、③、④的体积,据此找出规律解答即可。
【详解】第一个圆柱体的体积为:π×(2÷2)2×1=π×1;第二个圆柱体的体积为:π×(4÷2)2×2=π×23;第三个圆柱体的体积为:π×(6÷2)2×3=π×33;第四个圆柱依的体积为:π×(8÷2)2× 4 = π×43 ……,所以第n个圆柱体的体积为:πn3。
故答案为:D
【点睛】此题考查了圆柱体积公式的应用,关键是熟记公式。
8.B
【分析】观察图形可知,甲图增加的面积是2个半径为r的圆的面积,根据圆的面积公式:π×半径2,求出增加的面;乙图增加的面积是2个长是底面直径,宽是圆柱的高的长方形面积;根据长方形面积公式:长×宽;求出增加的面积,即可解答。
【详解】甲图增加的面积:
π×r2×2
=2πr2
乙图增加的面积:
r×2×h×2
=4rh
故答案为:B
【点睛】利用圆的面积公式、长方形面积公式进行解答,关键明确两个圆柱横切面的面的形状是解答本题的关键。
9.9
【分析】根据题意可知,圆柱的体积等于圆锥的体积,底面积相等;圆柱的体积公式:体积=圆柱的底面积×圆柱的高;圆锥的体积公式:体积=圆锥的底面积×圆锥的高×;即圆柱的底面积×圆柱的高=圆锥的底面积×圆锥的高×;圆锥的高=圆柱的高×3,代入数据,即可解答。
【详解】3×3=9(厘米)
【点睛】根据圆柱与圆锥的体积关系进行解答,关键明确等底等体积的圆锥的高是圆柱高的3倍。
10.640
【分析】等底等高的圆锥的体积是圆柱体积的,所以这个陀螺圆锥部分的体积相当于原圆柱体积的,用乘法求得圆锥的体积,然后用圆锥体积加上原来圆柱体积的即可。
【详解】960×+960××
=480+480×
=480+160
=640(cm3)
【点睛】此题考查的是理解掌握等底等高的圆柱和圆锥体积之间的关系及应用。
11.100.48
【分析】根据题意可知:把这个圆锥从顶点向底面做垂直切割,表面积增加48平方厘米,表面积增加的是两个以圆锥的高为高,圆锥的底面直径为底的三角形的面积,由此可以求出圆锥的底面直径,再根据圆锥的体积公式:,把数据代入公式解答。
【详解】圆锥的底面半径:
(厘米)
圆锥的体积:
(立方厘米)
【点睛】此题主要考查圆锥体积公式的灵活运用,重点是求出圆锥的底面半径.
12.6
【分析】根据圆柱的体积公式:圆柱体积=底面积×高,圆锥的体积=底面积×高×,带入数据,求出圆柱里果汁的体积和圆锥形玻璃杯的体积,再用果汁的体积除以圆锥形玻璃杯的体积,即可解答。
【详解】3.14×(10÷2)2×(8+8)÷[3.14×(10÷2)2×8×]
=3.14×25×16÷[3.14×25×8×]
=78.5×16÷[78.5×8×]
=1256÷[628×]
=1256÷
=1256×
=6(杯)
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
13. 12.56 3.14
【分析】根据题干分析可得,此题有两种不同的方法:(1)以长12.56分米为圆柱的底面周长,(2)以6.28分米为圆柱的底面周长,由此求出圆柱的底面半径,再根据圆的面积公式即可解决问题。
【详解】12.56÷3.14÷2=2(分米)
3.14×22
=3.14×4
=12.56(平方分米)
6.28÷3.14÷2=1(分米)
3.14×12
=3.14×1
=3.14(平方分米)
所以这个铁皮桶的底面积是12.56平方分米或3.14平方分米。
【点睛】解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高。
14. 36 12000
【分析】根据“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”,也就是说,圆锥的体积是1份,圆柱的体积是3份,那么它们的体积就相差2份;已知它们的体积相差24立方分米,用24除以2就是圆锥的体积,再用圆锥的体积乘3就是圆柱的体积。
【详解】24÷(3-1)
=24÷2
=12(立方分米)
12立方分米=12000立方厘米
12×3=36(立方分米)
【点睛】此题是考查体积的计算,可利用“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”来解答。要注意求的圆锥的体积单位是立方厘米。
15.√
【详解】试题分析:根据圆的面积公式S=πr2,知道当一个圆柱体和一个圆锥体的底面半径相等时,底面积相等;再根据圆柱的体积公式V=sh,圆锥的体积公式V=sh,知道在圆柱与圆锥的体积和底面积相等时,圆锥的高与圆柱的高的关系.
解:因为一个圆柱体和一个圆锥体的底面半径相等,
所以圆柱体和圆锥体的底面积相等,
又因为圆柱的体积是:V=sh1,
圆锥的体积:V=sh2,
所以sh1=sh2,
3h1=h2
所以h2÷h1=3,
故判断:√.
点评:此题主要是利用圆柱与圆锥的体积公式,推导出在底面积和体积分别相等时,圆锥的高与圆柱的高的关系.
16.×
【分析】圆柱的体积=πr2h,当圆柱的高度不变,底面半径扩大2倍时,现在圆柱的体积=π(r×2)2h=4×πr2h。
【详解】圆柱的高度不变,底面半径扩大2倍,圆柱的体积也扩大2×2=4倍。
故答案为∶×。
【点睛】本题考查了圆柱的体积,根据积的变化规律进行分析。
17.×
【分析】体积是指物体所占空间的大小;表面积是指所有立体图形外面的面积之和。
【详解】根据分析可知,做一个圆柱形玻璃鱼缸,需要多大面积的玻璃需要计算这个圆柱的表面积。
故答案为:×
【点睛】圆柱表面积和体积的区别是解答此题的关键,要掌握。
18.×
【分析】根据圆柱的特征:圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。圆柱有无数条高;圆锥的特征是:圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高。据此判断。
【详解】圆柱有无数条高,圆锥只有1条高,原题说法错误。
故答案为:错误。
【点睛】此题主要考查了圆柱和圆锥的特征。
19.√
【分析】圆柱延高展开得到的长方形的宽=圆柱的底面周长、长方形的长=圆柱的高,据此解答。
【详解】延高展开后得到的长方形的长是2πr,宽是:2πr
长=宽,所以延高展开得到一个正方形。
故答案为:√
【点睛】本题主要考查圆柱体的侧面展开图,解题时要明确:圆柱延高展开得到的长方形的宽=圆柱的底面周长、长方形的长=圆柱的高。
20.(1)314立方分米;(2)914平方分米;1785立方分米
【分析】(1)根据圆锥的体积=底面积×高÷3,解答即可;
(2)表面积=长方体的表面积+圆柱的侧面积,体积=长方体的体积+圆柱的体积。
【详解】(1)×3.14×(10÷2)2×12
=×3.14×25×12
=3.14×100
=314(立方分米)
体积是314立方分米。
(2)10×10×6+3.14×10×10
=600+314
=914(平方分米)
10×10×10+3.14×(10÷2)2×10
=1000+785
=1785(立方分米)
表面积是914平方分米,体积是1785立方分米。
21.292.02平方厘米
【分析】求至少用多少平方厘米的布料,就是求这个圆柱形水杯的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(6÷2)2+3.14×6×14
=3.14×9+18.84×14
=28.26+263.76
=292.03(平方厘米)
答:妈妈至少用了292.02平方厘米布料。
【点睛】本题主要考查圆柱的表面积公式的灵活运用,关键是熟记公式。
22.1.2厘米
【分析】根据题意可知,把圆锥形铁块从圆柱形玻璃容器中取出后,水面下降的高度等于圆锥的体积除以圆柱的底面积。根据圆锥的体积公式:V=πr2h,圆的面积公式:S=πr2,把数据代入解答。
【详解】31.4÷3.14÷2
=10÷2
=5(厘米)
×3.14×32×10÷(3.14×52)
=×3.14×9×10÷78.5
=94.2÷78.5
=1.2(厘米)
答:容器中水面高度将下降1.2厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,圆的面积公式及应用,关键是熟记公式。
23.282.6毫升
【分析】把圆柱体易拉罐的高看作单位“1”,直径比高少,直径是高的(1-),直径是6厘米,用6÷(1-)求出圆柱体易拉罐的高,再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】6÷(1-)
=6÷
=6×
=10(厘米)
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
答:这个易拉罐最多能装饮料282.6毫升。
【点睛】熟练掌握圆柱的体积公式是解答本题的关键。
24.125.6平方米
【分析】求抹水泥的面积,就是求这个无盖圆柱水池的表面积,根据圆柱表面积公式:底面积+侧面积,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×3
=3.14×16+25.12×3
=50.24+75.36
=125.6(平方米)
答:抹水泥部分的面积是125.6平方米。
【点睛】利用圆柱的表面积公式进行解答,关键是熟记公式。
25.小时
【分析】根据圆柱的容积(体积)公式:V=abh,求出这个水池的容积(装满水的体积),再求出三个进水管1小时注入水的体积,然后根据“包含”除法的意义,用除法解答。
【详解】3.14×(8÷2)2×2.5÷(12.56×3)
=3.14×40÷37.68
=125.6÷37.68
=(小时)
答:小时可以注满水池。
【点睛】此题主要考查圆柱的容积(体积)公式的灵活运用,关键是熟记公式。
26.100.48平方分米
【分析】乐乐将一个铁皮油桶在地上滚动一圈,其痕迹长就是油桶的底面周长,根据圆的周长公式:周长=π×2×半径;半径=周长÷π÷2;代入数据,求出油桶的底面半径;宽就是圆柱形油桶的高,根据圆柱的表面积=底面周长×高+底面积×2;代入数据,即可解答。
【详解】半径:12.56÷3.14÷2
=4÷2
=2(分米)
表面积:12.56×6+3.14×22×2
=75.36+3.14×4×2
=75.36+12.56×2
=75.36+25.12
=100.48(平方分米)
答:至少需要铁皮100.48平方分米。
【点睛】根据圆的周长公式、圆柱的表面积公式进行解答。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.用铁皮做一个高是5dm,底面直径是4dm的无盖圆柱形水桶,至少需要铁皮( )dm2。
A.263.76 B.87.92 C.62.8 D.75.36
2.贝贝过生日时,收到一个圆锥形陀螺,陀螺的底面直径是6cm,高是5cm。如果把它装在一个圆柱体盒子中,这个盒子的容积至少是( )cm3。
A.125.6 B.141.3 C.150.72 D.226.08
3.一个圆柱和一个圆锥底面半径的比是2∶3,它们的高相等,圆柱和圆锥的体积的最简整数比是( )。
A.9∶4 B.4∶9 C.3∶4 D.4∶3
4.如图,各杯中的饮料,( )。
A.A杯中的最少 B.B杯中的最少 C.C杯中的最少 D.同样多
5.一个圆柱的底面周长是18.84米,高是2米,则这个圆柱的表面积是( )平方米。
A.94.2 B.65.94 C.56.52 D.37.68
6.把一根长20分米的圆柱形木头沿横截面截成5段小圆柱形木头后,表面积比原来增加了80平方分米。这根圆柱形木头的体积是( )立方分米。
A.200 B.180 C.150 D.100
7.观察下面的圆柱,分析它们的底面直径和高的变化引起体积变化的规律,根据这个规律,用含有字母的式子表示第n个圆柱的体积是( )。
A.π2n B.πn2 C.π2n2 D.πn3
8.(如图)同一个圆柱切分后,表面积比原来增加4rh的图是( )。
A.甲 B.乙 C.两个都是 D.两个都不是
二、填空题
9.将一个高3厘米的橡皮泥圆柱捏成一个底面积和该圆柱底面积大小相同的圆锥,这个圆锥的高是( )厘米。
10.如图,把一个体积为960cm3的圆柱形木料削成一个陀螺,陀螺的体积为( )cm3。
11.把一个高是6厘米的圆锥从顶点向底面做垂直切割,表面积增加48平方厘米,这个圆锥的体积是( )立方厘米。
12.如图是一瓶已经喝了一些的果汁和一个圆锥形玻璃环,如果把瓶中的果汁倒入这个圆锥形玻璃杯中,那么可以倒满( )杯。(单位:cm)
13.把一张长12.56分米,宽6.28分米的长方形铁皮圈成一个圆柱铁皮桶,这个铁皮桶的底面积是( )或( )平方分米。(接头处忽略不计)
14.等底等高的圆柱和圆锥,体积差是24立方分米,圆柱的体积是( )立方分米,圆锥的体积是( )立方厘米。
三、判断题
15.有一个圆柱和一个圆锥的底面半径相等,体积也相等,那么圆锥的高是圆柱的高的3倍.( )
16.圆柱的高度不变,底面半径扩大2倍,圆柱的体积也扩大2倍。( )
17.做一个圆柱形玻璃鱼缸,需要多大面积的玻璃需要计算这个圆柱的体积。( )
18.圆柱和圆锥都有1条高。( )
19.一个圆柱的底面半径是r,高是2πr,那么它的侧面沿高展开是正方形。( )
四、图形计算
20.计算(1)的体积,计算(2)的表面积和体积。
(1) (2)
五、解答题
21.妈妈给笑笑的水杯做了一个带底的敞口布套,如图所示。妈妈至少用了多少平方厘米布料?(接头处忽略不计)
22.一个从里面量底面周长是31.4厘米,高是12厘米的圆柱形容器里装有一些水,水中浸没着一个底面半径是3厘米,高是10厘米的圆锥形铁块,如果把圆锥形铁块从水中取出,那么容器中水面高度将下降多少厘米?
23.某公司生产一种饮料,采用圆柱体易拉罐包装,从里面量,底面直径是6厘米,比高少,这个易拉罐最多能装饮料多少毫升?
24.为推进乡村振兴,某乡镇为圆梦社区修建了一个圆柱形水池,从里面量底面直径是8米,池深3米,在水池的底面和内壁涂上水泥,涂水泥部分的面积是多少平方米?
25.一个圆柱形水池,从里面量得它的底面直径是8米,深是2.5米,池上装有3根同样的进水管,每个管每小时可以注入水12.56立方米,三管齐开,几小时可以注满水池?
26.乐乐将一个铁皮油桶在地上滚动一圈,量得其痕迹长12.56分米、宽6分米。制作这个油桶至少需要铁皮多少平方分米?(桶口和盖忽略不计)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】已知这个水桶无盖,所以需要铁皮的面积等于这个圆柱侧面积加上一个底面的面积,根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】3.14×4×5+3.14×(4÷2)2
=12.56×5+3.14×4
=62.8+12.56
=75.36(平方分米)
答:至少需要铁皮75.36平方分米。
故答案为:D
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
2.B
【分析】根据题意可知,圆柱体盒子与圆锥等底等高,根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【详解】3.14×(6÷2)2×5
=3.14×9×5
=28.26×5
=141.3(cm3)
这个盒子的容积至少是141.3cm3。
故答案为:B
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
3.D
【分析】设圆柱的底面半径为2,则圆锥的底面半径为3,高均为h,分别求出圆柱、圆锥的体积,得出体积比并化简即可。
【详解】设圆柱的底面半径为2,则圆锥的底面半径为3,高均为h
圆柱的体积为:π×22×h=4πh
圆锥的体积为:×π×32×h=3πh
圆柱的体积∶圆锥的体积=4πh∶3πh=4∶3。
故答案为:D
【点睛】本题主要考查圆柱、圆锥的体积公式的灵活运用。
4.B
【分析】利用底面积乘饮料的高度即可比较体积大小,据此解答。
【详解】A.3.14×(4÷2)2×2
=3.14×4×2
=25.12(立方厘米)
B.3.14×(2÷2)2×4
=3.14×1×4
=12.56(立方厘米)
C.4×4×2
=16×2
=32(立方厘米)
因为12.56<25.12<32,所以B杯中的饮料最少。
故答案为:B
【点睛】本题考查了长方体、圆柱的体积公式的应用。
5.A
【分析】圆柱的表面积=侧面积+底面积×2,而圆柱的侧面积=底面周长×高。已知圆柱的底面周长,先根据“圆的周长=2πr”求出圆柱的底面半径,再根据“圆的面积=πr2”可以求出圆柱的底面积。分别把数据代入公式求出侧面积和底面积,最后求出圆柱的表面积。
【详解】18.84÷3.14÷2=3(米)
18.84×2+3.14×33×2
=37.68+56.52
=94.2(平方米)
故答案为:A
【点睛】本题考查圆柱的表面积。掌握并熟练运用圆柱的表面积、侧面积以及圆的周长和面积公式是解题的关键。
6.A
【分析】把圆柱形木头沿横截面截成5段小圆柱形木头,要切割4次,表面积比原来增加了4×2=8(个)横截面的面积,据此用80除以8即可求出横截面的面积。圆柱的体积=底面积×高=横截面面积×长,据此解答。
【详解】(5-1)×2=8(个)
80÷8×20
=10×20
=200(立方分米)
故答案为:A
【点睛】本题考查了立体图形的切拼和圆柱的体积。明确“圆柱的表面积比原来增加了8个横截面的面积”,从而求出横截面的面积是解题的关键。
7.D
【分析】根据圆柱体积公式:V=πr2h,依次计算出图①、②、③、④的体积,据此找出规律解答即可。
【详解】第一个圆柱体的体积为:π×(2÷2)2×1=π×1;第二个圆柱体的体积为:π×(4÷2)2×2=π×23;第三个圆柱体的体积为:π×(6÷2)2×3=π×33;第四个圆柱依的体积为:π×(8÷2)2× 4 = π×43 ……,所以第n个圆柱体的体积为:πn3。
故答案为:D
【点睛】此题考查了圆柱体积公式的应用,关键是熟记公式。
8.B
【分析】观察图形可知,甲图增加的面积是2个半径为r的圆的面积,根据圆的面积公式:π×半径2,求出增加的面;乙图增加的面积是2个长是底面直径,宽是圆柱的高的长方形面积;根据长方形面积公式:长×宽;求出增加的面积,即可解答。
【详解】甲图增加的面积:
π×r2×2
=2πr2
乙图增加的面积:
r×2×h×2
=4rh
故答案为:B
【点睛】利用圆的面积公式、长方形面积公式进行解答,关键明确两个圆柱横切面的面的形状是解答本题的关键。
9.9
【分析】根据题意可知,圆柱的体积等于圆锥的体积,底面积相等;圆柱的体积公式:体积=圆柱的底面积×圆柱的高;圆锥的体积公式:体积=圆锥的底面积×圆锥的高×;即圆柱的底面积×圆柱的高=圆锥的底面积×圆锥的高×;圆锥的高=圆柱的高×3,代入数据,即可解答。
【详解】3×3=9(厘米)
【点睛】根据圆柱与圆锥的体积关系进行解答,关键明确等底等体积的圆锥的高是圆柱高的3倍。
10.640
【分析】等底等高的圆锥的体积是圆柱体积的,所以这个陀螺圆锥部分的体积相当于原圆柱体积的,用乘法求得圆锥的体积,然后用圆锥体积加上原来圆柱体积的即可。
【详解】960×+960××
=480+480×
=480+160
=640(cm3)
【点睛】此题考查的是理解掌握等底等高的圆柱和圆锥体积之间的关系及应用。
11.100.48
【分析】根据题意可知:把这个圆锥从顶点向底面做垂直切割,表面积增加48平方厘米,表面积增加的是两个以圆锥的高为高,圆锥的底面直径为底的三角形的面积,由此可以求出圆锥的底面直径,再根据圆锥的体积公式:,把数据代入公式解答。
【详解】圆锥的底面半径:
(厘米)
圆锥的体积:
(立方厘米)
【点睛】此题主要考查圆锥体积公式的灵活运用,重点是求出圆锥的底面半径.
12.6
【分析】根据圆柱的体积公式:圆柱体积=底面积×高,圆锥的体积=底面积×高×,带入数据,求出圆柱里果汁的体积和圆锥形玻璃杯的体积,再用果汁的体积除以圆锥形玻璃杯的体积,即可解答。
【详解】3.14×(10÷2)2×(8+8)÷[3.14×(10÷2)2×8×]
=3.14×25×16÷[3.14×25×8×]
=78.5×16÷[78.5×8×]
=1256÷[628×]
=1256÷
=1256×
=6(杯)
【点睛】熟练掌握和灵活运用圆柱的体积公式和圆锥的体积公式是解答本题的关键。
13. 12.56 3.14
【分析】根据题干分析可得,此题有两种不同的方法:(1)以长12.56分米为圆柱的底面周长,(2)以6.28分米为圆柱的底面周长,由此求出圆柱的底面半径,再根据圆的面积公式即可解决问题。
【详解】12.56÷3.14÷2=2(分米)
3.14×22
=3.14×4
=12.56(平方分米)
6.28÷3.14÷2=1(分米)
3.14×12
=3.14×1
=3.14(平方分米)
所以这个铁皮桶的底面积是12.56平方分米或3.14平方分米。
【点睛】解答此题的关键是明白:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高。
14. 36 12000
【分析】根据“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”,也就是说,圆锥的体积是1份,圆柱的体积是3份,那么它们的体积就相差2份;已知它们的体积相差24立方分米,用24除以2就是圆锥的体积,再用圆锥的体积乘3就是圆柱的体积。
【详解】24÷(3-1)
=24÷2
=12(立方分米)
12立方分米=12000立方厘米
12×3=36(立方分米)
【点睛】此题是考查体积的计算,可利用“等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍”来解答。要注意求的圆锥的体积单位是立方厘米。
15.√
【详解】试题分析:根据圆的面积公式S=πr2,知道当一个圆柱体和一个圆锥体的底面半径相等时,底面积相等;再根据圆柱的体积公式V=sh,圆锥的体积公式V=sh,知道在圆柱与圆锥的体积和底面积相等时,圆锥的高与圆柱的高的关系.
解:因为一个圆柱体和一个圆锥体的底面半径相等,
所以圆柱体和圆锥体的底面积相等,
又因为圆柱的体积是:V=sh1,
圆锥的体积:V=sh2,
所以sh1=sh2,
3h1=h2
所以h2÷h1=3,
故判断:√.
点评:此题主要是利用圆柱与圆锥的体积公式,推导出在底面积和体积分别相等时,圆锥的高与圆柱的高的关系.
16.×
【分析】圆柱的体积=πr2h,当圆柱的高度不变,底面半径扩大2倍时,现在圆柱的体积=π(r×2)2h=4×πr2h。
【详解】圆柱的高度不变,底面半径扩大2倍,圆柱的体积也扩大2×2=4倍。
故答案为∶×。
【点睛】本题考查了圆柱的体积,根据积的变化规律进行分析。
17.×
【分析】体积是指物体所占空间的大小;表面积是指所有立体图形外面的面积之和。
【详解】根据分析可知,做一个圆柱形玻璃鱼缸,需要多大面积的玻璃需要计算这个圆柱的表面积。
故答案为:×
【点睛】圆柱表面积和体积的区别是解答此题的关键,要掌握。
18.×
【分析】根据圆柱的特征:圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。圆柱有无数条高;圆锥的特征是:圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高。据此判断。
【详解】圆柱有无数条高,圆锥只有1条高,原题说法错误。
故答案为:错误。
【点睛】此题主要考查了圆柱和圆锥的特征。
19.√
【分析】圆柱延高展开得到的长方形的宽=圆柱的底面周长、长方形的长=圆柱的高,据此解答。
【详解】延高展开后得到的长方形的长是2πr,宽是:2πr
长=宽,所以延高展开得到一个正方形。
故答案为:√
【点睛】本题主要考查圆柱体的侧面展开图,解题时要明确:圆柱延高展开得到的长方形的宽=圆柱的底面周长、长方形的长=圆柱的高。
20.(1)314立方分米;(2)914平方分米;1785立方分米
【分析】(1)根据圆锥的体积=底面积×高÷3,解答即可;
(2)表面积=长方体的表面积+圆柱的侧面积,体积=长方体的体积+圆柱的体积。
【详解】(1)×3.14×(10÷2)2×12
=×3.14×25×12
=3.14×100
=314(立方分米)
体积是314立方分米。
(2)10×10×6+3.14×10×10
=600+314
=914(平方分米)
10×10×10+3.14×(10÷2)2×10
=1000+785
=1785(立方分米)
表面积是914平方分米,体积是1785立方分米。
21.292.02平方厘米
【分析】求至少用多少平方厘米的布料,就是求这个圆柱形水杯的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(6÷2)2+3.14×6×14
=3.14×9+18.84×14
=28.26+263.76
=292.03(平方厘米)
答:妈妈至少用了292.02平方厘米布料。
【点睛】本题主要考查圆柱的表面积公式的灵活运用,关键是熟记公式。
22.1.2厘米
【分析】根据题意可知,把圆锥形铁块从圆柱形玻璃容器中取出后,水面下降的高度等于圆锥的体积除以圆柱的底面积。根据圆锥的体积公式:V=πr2h,圆的面积公式:S=πr2,把数据代入解答。
【详解】31.4÷3.14÷2
=10÷2
=5(厘米)
×3.14×32×10÷(3.14×52)
=×3.14×9×10÷78.5
=94.2÷78.5
=1.2(厘米)
答:容器中水面高度将下降1.2厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,圆的面积公式及应用,关键是熟记公式。
23.282.6毫升
【分析】把圆柱体易拉罐的高看作单位“1”,直径比高少,直径是高的(1-),直径是6厘米,用6÷(1-)求出圆柱体易拉罐的高,再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】6÷(1-)
=6÷
=6×
=10(厘米)
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
答:这个易拉罐最多能装饮料282.6毫升。
【点睛】熟练掌握圆柱的体积公式是解答本题的关键。
24.125.6平方米
【分析】求抹水泥的面积,就是求这个无盖圆柱水池的表面积,根据圆柱表面积公式:底面积+侧面积,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×3
=3.14×16+25.12×3
=50.24+75.36
=125.6(平方米)
答:抹水泥部分的面积是125.6平方米。
【点睛】利用圆柱的表面积公式进行解答,关键是熟记公式。
25.小时
【分析】根据圆柱的容积(体积)公式:V=abh,求出这个水池的容积(装满水的体积),再求出三个进水管1小时注入水的体积,然后根据“包含”除法的意义,用除法解答。
【详解】3.14×(8÷2)2×2.5÷(12.56×3)
=3.14×40÷37.68
=125.6÷37.68
=(小时)
答:小时可以注满水池。
【点睛】此题主要考查圆柱的容积(体积)公式的灵活运用,关键是熟记公式。
26.100.48平方分米
【分析】乐乐将一个铁皮油桶在地上滚动一圈,其痕迹长就是油桶的底面周长,根据圆的周长公式:周长=π×2×半径;半径=周长÷π÷2;代入数据,求出油桶的底面半径;宽就是圆柱形油桶的高,根据圆柱的表面积=底面周长×高+底面积×2;代入数据,即可解答。
【详解】半径:12.56÷3.14÷2
=4÷2
=2(分米)
表面积:12.56×6+3.14×22×2
=75.36+3.14×4×2
=75.36+12.56×2
=75.36+25.12
=100.48(平方分米)
答:至少需要铁皮100.48平方分米。
【点睛】根据圆的周长公式、圆柱的表面积公式进行解答。
答案第1页,共2页
答案第1页,共2页
