5.3平行线的性质(同步练习)(含答案)2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 5.3平行线的性质(同步练习)(含答案)2022-2023学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 624.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 19:29:53 | ||
图片预览


文档简介
5.3平行线的性质
(同步练习)
一、单选题
1.如图,△OAB为等腰直角三角形(∠A=∠B=45°,∠AOB=90°),△OCD为等边三角形(∠C=∠D=∠COD=60°),满足OC>OA,△OCD绕点O从射线OC与射线OA重合的位置开始,逆时针旋转,旋转的角度为α(0°<α<360°),下列说法正确的是( )
A.当α=15°时,DC∥AB
B.当OC⊥AB时,α=45°
C.当边OB与边OD在同一直线上时,直线DC与直线AB相交形成的锐角为15°
D.整个旋转过程,共有10个位置使得△OAB与△OCD有一条边平行
2.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中,都与地面l平行,,.当为( )度时,与平行.
A.16 B.60 C.66 D.114
3.设a,b,c为互不相等的实数,且,则下列结论正确的是( )
A. B. C. D.
4.如图,ABCD,AD⊥AC,∠BAD=35°,则∠ACD=( )
A.35° B.45° C.55° D.70°
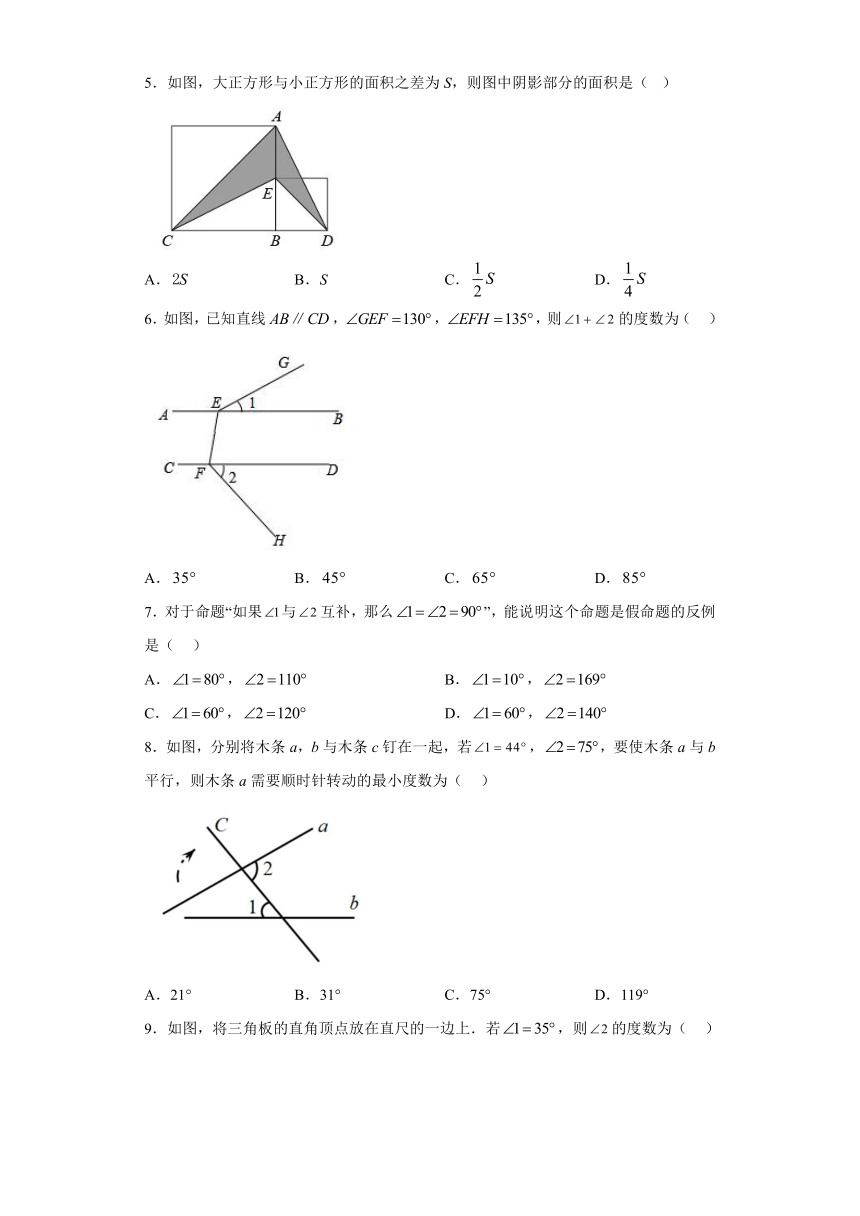
5.如图,大正方形与小正方形的面积之差为S,则图中阴影部分的面积是( )
A. B.S C. D.
6.如图,已知直线,,,则的度数为( )
A. B. C. D.
7.对于命题“如果与互补,那么”,能说明这个命题是假命题的反例是( )
A., B.,
C., D.,
8.如图,分别将木条a,b与木条c钉在一起,若,,要使木条a与b平行,则木条a需要顺时针转动的最小度数为( )
A.21° B.31° C.75° D.119°
9.如图,将三角板的直角顶点放在直尺的一边上.若,则的度数为( )
A.45° B.50° C.55° D.65°
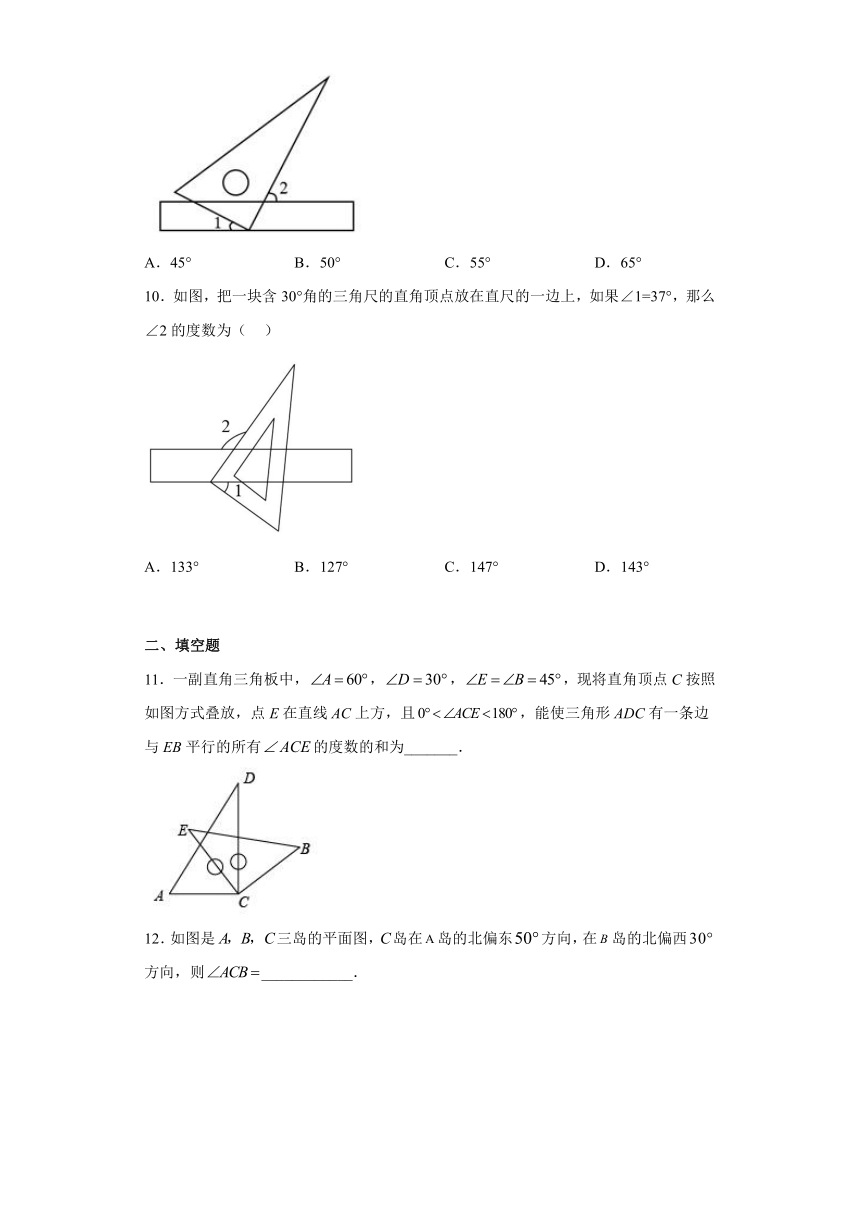
10.如图,把一块含30°角的三角尺的直角顶点放在直尺的一边上,如果∠1=37°,那么∠2的度数为( )
A.133° B.127° C.147° D.143°
二、填空题
11.一副直角三角板中,,,,现将直角顶点C按照如图方式叠放,点E在直线AC上方,且,能使三角形ADC有一条边与EB平行的所有的度数的和为_______.
12.如图是三岛的平面图,岛在岛的北偏东方向,在岛的北偏西方向,则____________.
13.如图所示,一个三角尺的直角顶点放在直线上,量得,则____.
14.如图,,,且三角形的面积为,则点到的距离为________.
15.如图,,,则∠2等于______.
三、解答题
16.课题学行线的“等角转化”功能.
(1)阅读理解:如图1,已知点A是外一点,连接、,求的度数.阅读并补充下面推理过程.
解:过点A作,
, ,
,
.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将、、“凑”在一起,得出角之间的关系,使问题得以解决.
(2)方法运用:如图2,已知,求的度数;
(3)深化拓展:已知,点C在点D的右侧,,平分,平分,,所在的直线交于点E,点E在直线与之间.
①如图3,点B在点A的左侧,若,求的度数.
②如图4,点B在点A的右侧,且,.若,求度数.(用含n的代数式表示)
17.指出下列命题的题设和结论,并判断它们是真命题还是假命题,如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
18.如图1,潜望镜是指从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地面上活动的装置.其构造与普通地上望远镜相同,唯另加两个反射镜使物光经两次反射而折向眼中.潜望镜常用于潜水艇,坑道和坦克内用以观察敌情.光线经过镜子反射时,抽象出的数学图形如图2所示,已知,AB∥CD,∠1=∠2,请问进入潜望镜光线EA和出潜望镜光线DF是否平行?并说明理由.
19.探究:如图①,在中,点,,分别是边,,上,且,∥,若,求的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
解:∵
∴∥(_____________________________)
∴____________(_______________________)
∵∥
∴_________(_____________________)
∴
∵
∴_____________
应用:如图②,在中,点,,分别是边,,的延长线上,且,∥,若,则的大小为_____________(用含的代数式表示).
20.如图,点B,C在线段的异侧,点E,F分别是线段,上的点,已知,.
(1)求证:;
(2)若,求证:;
(3)在(2)的条件下,若,求的度数.
21.将一副三角板中的两块直角三角尺顶点C按照如图①方式叠放在一起(其中,,,)设.
(1)若,说明;
(2)将三角形CDE绕点C顺时针转动,若,求的度数.
参考答案:
1.A2.C3.D4.C5.C6.D7.C8.B9.C10.B
11.345°
12.
13.30°
14.4
15.37°
16.(1);
(2)
(3)①;②
17.(1)题设:如果两个角的和等于平角时,结论:那么这两个角互为补角;是真命题;(2)题设:如果两个角是内错角,那么这两个角相等;是假命题,反例见解析;(3)题设:如果两条平行线被第三条直线所截,结论:那么内错角相等.是真命题.
18.解:进入潜望镜光线EA和出潜望镜光线DF是平行的,理由如下
∵AB//CD
∴∠BAD=∠CDA
∵
∴,即
∴AE//DF
19.(1)同位角相等,两直线平行;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等; 65°;(2)180°-β
20.(1)证明:∵,,,
∴,
∴;
(2)证明:∵,,
∴,
∴,
∴;
(3)解:∵,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
21.(1)解:如图①中,
∵∠,,
∴∠ACE=∠A,
∴;
(2)解:如图②中,当时,则,
;
如图③中,当时,则,
.
综上所述,的值为15°或165°.
(同步练习)
一、单选题
1.如图,△OAB为等腰直角三角形(∠A=∠B=45°,∠AOB=90°),△OCD为等边三角形(∠C=∠D=∠COD=60°),满足OC>OA,△OCD绕点O从射线OC与射线OA重合的位置开始,逆时针旋转,旋转的角度为α(0°<α<360°),下列说法正确的是( )
A.当α=15°时,DC∥AB
B.当OC⊥AB时,α=45°
C.当边OB与边OD在同一直线上时,直线DC与直线AB相交形成的锐角为15°
D.整个旋转过程,共有10个位置使得△OAB与△OCD有一条边平行
2.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中,都与地面l平行,,.当为( )度时,与平行.
A.16 B.60 C.66 D.114
3.设a,b,c为互不相等的实数,且,则下列结论正确的是( )
A. B. C. D.
4.如图,ABCD,AD⊥AC,∠BAD=35°,则∠ACD=( )
A.35° B.45° C.55° D.70°
5.如图,大正方形与小正方形的面积之差为S,则图中阴影部分的面积是( )
A. B.S C. D.
6.如图,已知直线,,,则的度数为( )
A. B. C. D.
7.对于命题“如果与互补,那么”,能说明这个命题是假命题的反例是( )
A., B.,
C., D.,
8.如图,分别将木条a,b与木条c钉在一起,若,,要使木条a与b平行,则木条a需要顺时针转动的最小度数为( )
A.21° B.31° C.75° D.119°
9.如图,将三角板的直角顶点放在直尺的一边上.若,则的度数为( )
A.45° B.50° C.55° D.65°
10.如图,把一块含30°角的三角尺的直角顶点放在直尺的一边上,如果∠1=37°,那么∠2的度数为( )
A.133° B.127° C.147° D.143°
二、填空题
11.一副直角三角板中,,,,现将直角顶点C按照如图方式叠放,点E在直线AC上方,且,能使三角形ADC有一条边与EB平行的所有的度数的和为_______.
12.如图是三岛的平面图,岛在岛的北偏东方向,在岛的北偏西方向,则____________.
13.如图所示,一个三角尺的直角顶点放在直线上,量得,则____.
14.如图,,,且三角形的面积为,则点到的距离为________.
15.如图,,,则∠2等于______.
三、解答题
16.课题学行线的“等角转化”功能.
(1)阅读理解:如图1,已知点A是外一点,连接、,求的度数.阅读并补充下面推理过程.
解:过点A作,
, ,
,
.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将、、“凑”在一起,得出角之间的关系,使问题得以解决.
(2)方法运用:如图2,已知,求的度数;
(3)深化拓展:已知,点C在点D的右侧,,平分,平分,,所在的直线交于点E,点E在直线与之间.
①如图3,点B在点A的左侧,若,求的度数.
②如图4,点B在点A的右侧,且,.若,求度数.(用含n的代数式表示)
17.指出下列命题的题设和结论,并判断它们是真命题还是假命题,如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
18.如图1,潜望镜是指从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地面上活动的装置.其构造与普通地上望远镜相同,唯另加两个反射镜使物光经两次反射而折向眼中.潜望镜常用于潜水艇,坑道和坦克内用以观察敌情.光线经过镜子反射时,抽象出的数学图形如图2所示,已知,AB∥CD,∠1=∠2,请问进入潜望镜光线EA和出潜望镜光线DF是否平行?并说明理由.
19.探究:如图①,在中,点,,分别是边,,上,且,∥,若,求的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
解:∵
∴∥(_____________________________)
∴____________(_______________________)
∵∥
∴_________(_____________________)
∴
∵
∴_____________
应用:如图②,在中,点,,分别是边,,的延长线上,且,∥,若,则的大小为_____________(用含的代数式表示).
20.如图,点B,C在线段的异侧,点E,F分别是线段,上的点,已知,.
(1)求证:;
(2)若,求证:;
(3)在(2)的条件下,若,求的度数.
21.将一副三角板中的两块直角三角尺顶点C按照如图①方式叠放在一起(其中,,,)设.
(1)若,说明;
(2)将三角形CDE绕点C顺时针转动,若,求的度数.
参考答案:
1.A2.C3.D4.C5.C6.D7.C8.B9.C10.B
11.345°
12.
13.30°
14.4
15.37°
16.(1);
(2)
(3)①;②
17.(1)题设:如果两个角的和等于平角时,结论:那么这两个角互为补角;是真命题;(2)题设:如果两个角是内错角,那么这两个角相等;是假命题,反例见解析;(3)题设:如果两条平行线被第三条直线所截,结论:那么内错角相等.是真命题.
18.解:进入潜望镜光线EA和出潜望镜光线DF是平行的,理由如下
∵AB//CD
∴∠BAD=∠CDA
∵
∴,即
∴AE//DF
19.(1)同位角相等,两直线平行;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等; 65°;(2)180°-β
20.(1)证明:∵,,,
∴,
∴;
(2)证明:∵,,
∴,
∴,
∴;
(3)解:∵,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
21.(1)解:如图①中,
∵∠,,
∴∠ACE=∠A,
∴;
(2)解:如图②中,当时,则,
;
如图③中,当时,则,
.
综上所述,的值为15°或165°.
