第四单元正比例与反比例常考易错检测卷(单元测试) 小学数学六年级下册北师大版(含答案)
文档属性
| 名称 | 第四单元正比例与反比例常考易错检测卷(单元测试) 小学数学六年级下册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 00:00:00 | ||
图片预览



文档简介
第四单元正比例与反比例常考易错检测卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.已知=c(a,b均不为0),当哪个量一定时,另外两个量成正比例?( )
A.a B.b C.c D.都不是
2.龙龙制作了一个摩天轮模型,模型高度与摩天轮的实际高度之比是3∶400,现测得模型的高度为27cm,则摩天轮的实际高度是( )米。
A.27 B.33 C.36 D.42
3.下面说法错误的是( )。
A.如果a∶b=c∶d,那么a∶c=b∶d
B.将一个图形按2∶1的比放大,得到的图形与原来图形面积的比还是2∶1
C.4,5,24,30这四个数可以组成比例
D.平行四边形的面积一定,它的底和高成反比例
4.( )中的两个量不成正比例。
A.订阅某期刊的份数一定,单价和总钱数
B.一箱苹果,吃掉的个数和剩下的个数
C.长方体的底面积一定,高和体积
D.在同一个正方形中,正方形的周长和边长
5.A和B是两种相关联的量,已知A×B=7,则A和B( )。
A.成正比例 B.成反比例 C.不成比例 D.没有关系
6.能够表示a和b这两种量成正比例关系的是( )。
A.a+b=8 B.a-b=8 C.a×b=8 D.a÷b=8
二、填空题
7.表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填( );如果A和B成反比例关系,那么应填( )。
A 3 6
B 7
8.若,则与成( )比例关系;若,则与成( )比例关系。(填“正”或“反”)
9.一个三角形的面积是,它的底和高成( )比例。
10.一辆车匀速行驶,路程是s千米,时间是t小时,路程和时间的比值是( ),路程和时间成( )比例。
11.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如表。每块地砖的面积与所需地砖的数量成( )比例关系,如果每块地砖的面积是0.5m2,铺教室地面需要( )块地砖;如果铺教室地面用了150块地砖,所用地砖每块的面积是( )。
每块地砖面积/ 0.2 0.3 0.4 0.6 …
所需地砖数量/块 600 400 300 200 …
12.某工厂生产一批零件,每天生产的个数与需要的天数如下表。
每天生产的个数/个 200 300 400 500
需要的天数/天 30 20 15 12
(1)每天生产的个数与需要的天数成( )比例。(填“正”或“反”)
(2)如果该工厂每天生产250个零件,需要( )天。
13.一份稿件,甲单独打需小时,乙单独打需小时,甲和乙的工作效率比是( )。
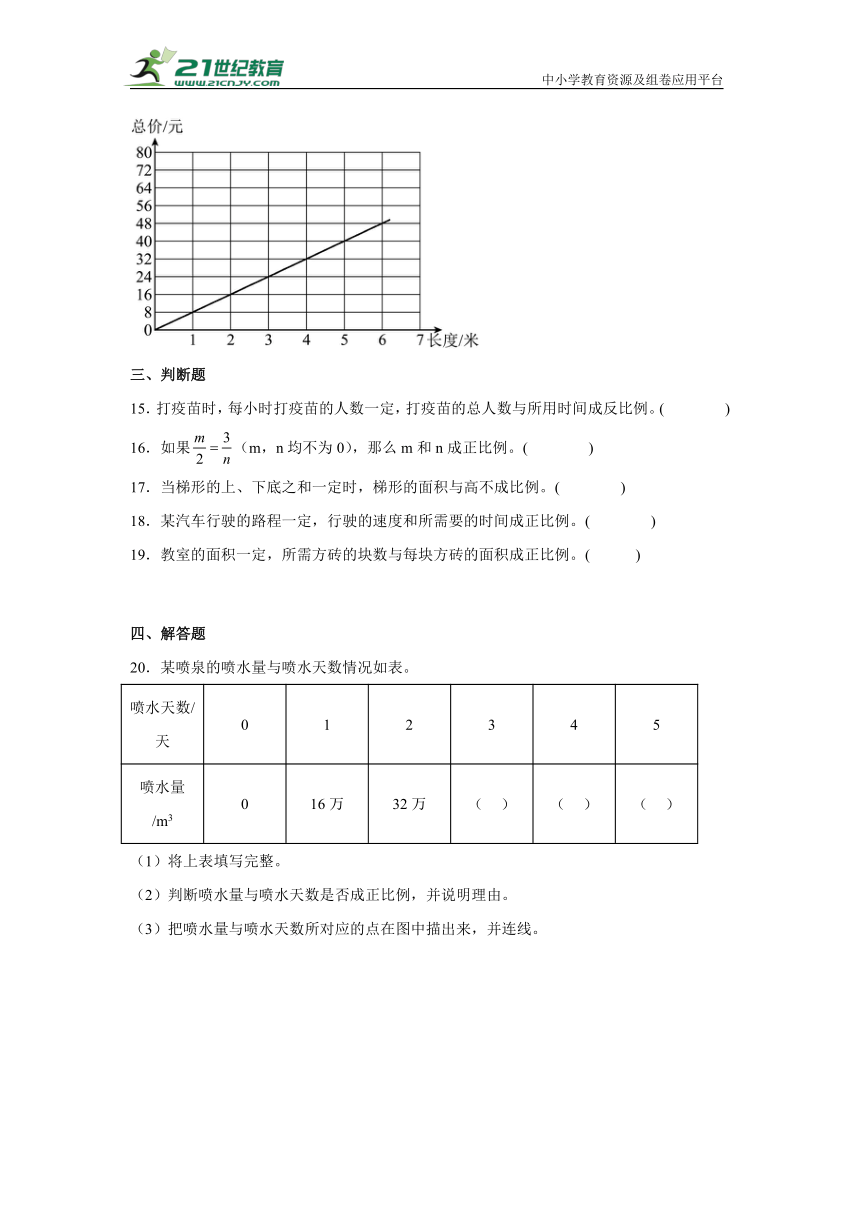
14.学校手工社团买了一种彩带,买的长度和总价关系如图:买10米这种彩带要花( )元,200元可以买( )米。
三、判断题
15.打疫苗时,每小时打疫苗的人数一定,打疫苗的总人数与所用时间成反比例。( )
16.如果(m,n均不为0),那么m和n成正比例。( )
17.当梯形的上、下底之和一定时,梯形的面积与高不成比例。( )
18.某汽车行驶的路程一定,行驶的速度和所需要的时间成正比例。( )
19.教室的面积一定,所需方砖的块数与每块方砖的面积成正比例。( )
四、解答题
20.某喷泉的喷水量与喷水天数情况如表。
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 ( ) ( ) ( )
(1)将上表填写完整。
(2)判断喷水量与喷水天数是否成正比例,并说明理由。
(3)把喷水量与喷水天数所对应的点在图中描出来,并连线。
(4)利用图像估计一下,3.5天的喷水量是( )m3;40万m3的喷水量需要喷( )天。
21.亮亮看一本故事书,平均每天看的页数和所用的时间如表。
平均每天看的页数/页 8 10 15 20 30
所用的时间/天 30 24 8
(1)将上表补充完整。
(2)平均每天看的页数与所用的时间是不是成反比例?说明理由。
(3)如果亮亮用40天看完了这本故事书,平均每天看多少页?
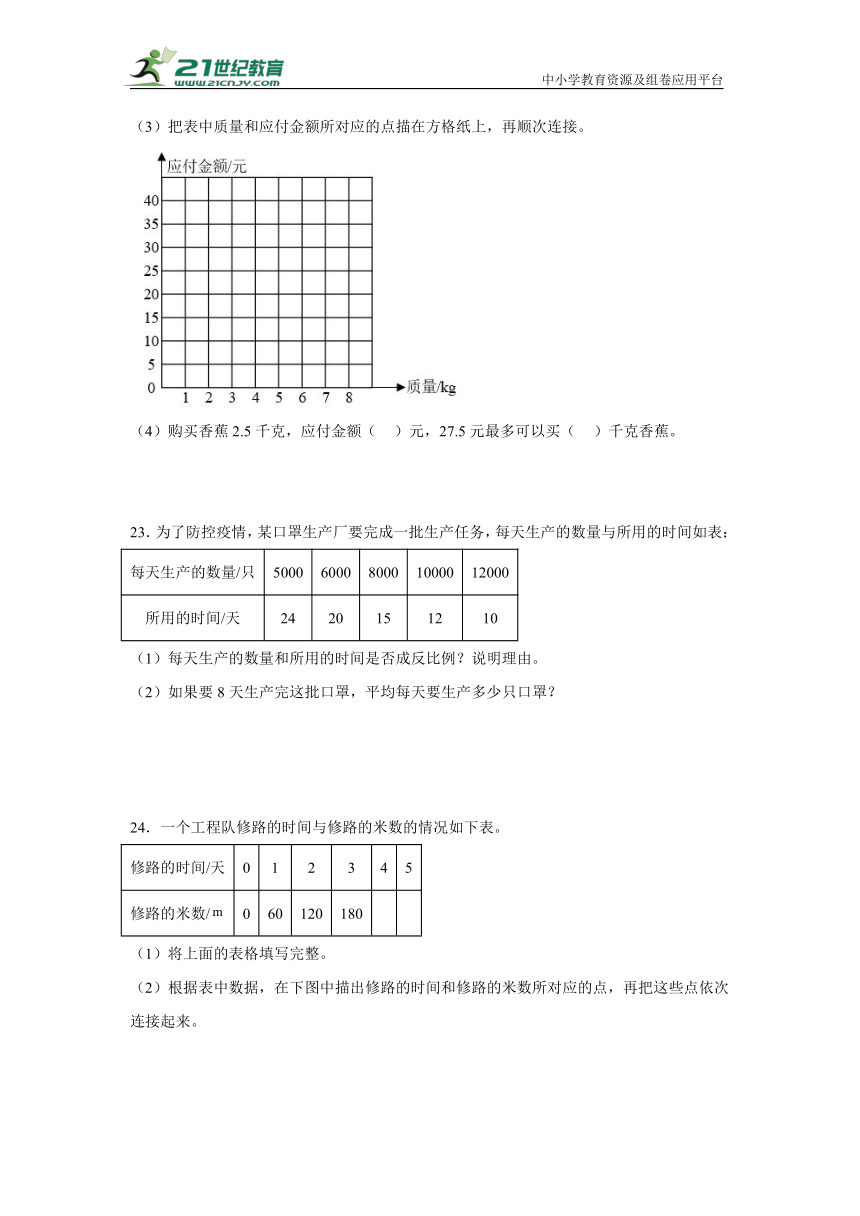
22.购买香蕉的质量和应付金额如表。
质量/kg 0 1 2 3 4 5 6 …
应付金额/元 0 5 10 15 20 …
(1)把上表填写完整。
(2)判断购买香蕉的质量与应付金额是否成正比例,并说明理由。
(3)把表中质量和应付金额所对应的点描在方格纸上,再顺次连接。
(4)购买香蕉2.5千克,应付金额( )元,27.5元最多可以买( )千克香蕉。
23.为了防控疫情,某口罩生产厂要完成一批生产任务,每天生产的数量与所用的时间如表:
每天生产的数量/只 5000 6000 8000 10000 12000
所用的时间/天 24 20 15 12 10
(1)每天生产的数量和所用的时间是否成反比例?说明理由。
(2)如果要8天生产完这批口罩,平均每天要生产多少只口罩?
24.一个工程队修路的时间与修路的米数的情况如下表。
修路的时间/天 0 1 2 3 4 5
修路的米数/ 0 60 120 180
(1)将上面的表格填写完整。
(2)根据表中数据,在下图中描出修路的时间和修路的米数所对应的点,再把这些点依次连接起来。
(3)如果修8天路,可以修( )米。
(4)工程队修路的时间与修路的米数是否成正比例关系?为什么?
25.李师傅要加工一批零件,每小时加工零件个数与加工时间如下表。
每小时加工零件的个数/个 20 30 40 60 …
加工的时间/时 12 8 6 4 …
(1)每小时加工零件个数与加工时间是否成反比例关系?为什么?
(2)如果李师傅每小时加工48个零件,需要多少小时完成?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定,据此解答;
【详解】=c(a,b均不为0),c也不为0,当c一定时,b和a成正比例。
已知=c(a,b均不为0)。当c一定时,另外两个量成正比例。
故答案为:C
【点睛】熟练掌握正比例意义是解答本题的关键。
2.C
【分析】设摩天轮的实际高度是x米,根据摩天轮的实际高度与模型高度的比值是一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【详解】解:设摩天轮的实际高度是x米,由题意得:
27厘米=0.27米
0.27: x =3:400
3x=0.27×400
3x÷3=0.27×400÷3
x=108÷3
x=36
摩天轮的实际高度是36米
故答案为:C
【点睛】本题考查了正反比例应用题,关键是得出摩天轮实际高度与模型高度的比值是一定的。
3.B
【分析】根据比的基本性质:两个内项之积等于两个外项之积;
图形放大或缩小后,对应边长的比相等,周长的比相等,但面积的比不相等;
比例的意义:表示两个比相等的式子,叫做比例;
再根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此逐项分析判断解答。
【详解】A.a∶b=c∶d;所以ad=bc;即a∶c=b∶d,
原题干正确,不符合题意;
B.将一个图形按2∶1比放大,假设这个图形是正方形,得到的图形与原来图形面积的比是:
(2×2)∶(1×1)
=4∶1
原题干说法错误,符合题意;
C.因为24∶4=6;30∶5=6,所以24∶4=30∶5,
4,5,24,30这四个数可以组成比例;
原题干说法正确,不符合题意;
D.底×高=平行四边形面积(一定),底和高成反比例,原题干说法确定,不符合题意。
故答案为:B
【点睛】本题考查的知识点较多,要逐项分析进行解答。
4.B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【详解】A.总价÷单价=数量(一定),比值一定,单价和总钱数成正比例关系。
B.一箱苹果的总个数-吃掉的个数=剩下的个数,比值和积都不一定,吃掉的个数和剩下的个数不成比例;
C.长方体的体积÷高=底面积(一定),比值一定,高和体积成正比例关系;
D.边长=周长÷4(一定),比值一定,在同一个正方形中,正方形的周长和边长成正比例关系;
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
5.B
【分析】根据数量关系判断是商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例,其他关系不成比例。
【详解】根据分析可知,A×B=7,乘积一定,故A和B成反比例。
故答案为:B
【点睛】此题主要考查学生对正、反比例判定的理解与应用。
6.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此,对选项逐一分析即可。
【详解】A.a+b=8,a和b这两种量既不是比值一定,也不是乘积一定,所以二者不成比例;
B.a-b=8,a和b这两种量既不是比值一定,也不是乘积一定,所以二者不成比例;
C.a×b=8,a和b这两种量乘积一定,等于8,所以二者成反比例;
D.a÷b=8,a和b这两种量比值一定,等于8,所以二者成正比例。
故答案为:D
【点睛】本题属于辨识正反比例的量,主要看两个量是比值一定,还是乘积一定,据此作出判断即可。
7. 14 3.5
【分析】如果A和B成正比例关系,则3与7的比等于6与方框内数的比;如果A和B成反比例关系,则3与7的积等于6与方框内数的积。
【详解】解:设方框内的数为x。
如果A和B成正比例关系,则
3:7=6:x
3x=7×6
3x÷3=42÷3
x=14
表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填14;
如果A和B成反比例关系,则
6x=3×7
6x÷6=21÷6
x=3.5
如果A和B成反比例关系,那么应填3.5。
【点睛】两种相关联的量,若其成正比例关系,则其比值一定;若其成反比例关系,则其乘积一定。
8. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此分析题目即可解答。
【详解】(一定),乘积一定,所以x与y成反比例关系;
(一定),比值一定,所以x与y成正比例关系。
【点睛】本题是一道关于正反比例的题目,可依据判断正反比例的方法求解。
9.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】三角形的底高面积
因为三角形的面积为
所以三角形的底高(一定),三角形的底和高乘积一定,所以底和高成反比例。
【点睛】掌握正反比例的意义是解答此题的关键。
10. 正
【分析】根据速度=路程÷时间,可知路程和时间的比值是速度,比值一定时,路程和时间成正比例,据此解答即可。
【详解】由分析可知;一辆车匀速行驶,路程是s千米,时间是t小时,路程和时间的比值是,路程和时间成正比例。
【点睛】根据路程、时间、速度的关系和正比例的判定方法,解答此题即可。
11. 反 240 0.8
【分析】判断两个相关联的量之间成什么比例,就看这两种量对应的是比值一定,还剩乘积一定,如果是比值一定,就成正比例;如果乘积一定,就成反比例;用每块地砖的面积与所需地砖的数量的乘积除以每块地砖的面积,求出需要地砖的块数;用每块地砖的面与所需地砖的数量的乘积除以地砖的块数,求出每块地砖的面积,据此解答。
【详解】0.2×600=0.3×400=0.4×300=0.6×200=120(一定);乘积一定,每块地砖的面积与所需地砖的数量成反比例;
120÷0.5=240(块)
120÷150=0.8(平方米)
【点睛】根据正比例意义和辨识,反比例意义和辨识进行解答。
12.(1)反
(2)24
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)用零件总个数÷每天生产的个数=需要天数,代入数据,即可解答。
(1)
200×30=300×20=400×15=500×12=6000(个),每天生产的个数与需要的天数乘积一定,所以每天生产的个数与需要的天数成反比例。
(2)
200×30÷250
=6000÷250
=24(天)
【点睛】根据正比例意义以及辨别和反比例意义以及辨别进行解答。
13.6∶5
【分析】根据工作量=工作效率×工作时间,可得工作量一定时,工作效率和工作时间成反比例,据此解答即可。
【详解】因为工作量一定,都是一份稿件,所以甲和乙工作效率比是:∶=6∶5
【点睛】解答此题的关键是要明确:工作量一定时,工作效率和工作时间成反比例。
14. 80 25
【分析】从图中可以看出总价和买的长度成正比例关系,8元对应的是1米,所以每米需要8元,那么10米就需要(8×10)元,200可以买(200÷8)米。
【详解】8×10=80(元)
200÷8=25(米)
所以买10米这种彩带要花80元,200元可以买25米。
【点睛】此题考查了学生对正比例关系的辨识及应用。
15.×
【分析】根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
【详解】打疫苗的总人数÷打疫苗所用的时间=每小时打疫苗的人数(一定),打疫苗的总人数与所用时间成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
16.×
【分析】根据比例的基本性质:两个内项之积等两个于外项之积;写出这个比例式mn=2×3,即mn=6;再根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此判断解答。
【详解】=(m,n均不为0),
mn=2×3,即mn=6(一定),m和n成反比例。
原题干说法错误。
故答案为:×
【点睛】掌握比例的基本性质和辨识成正、反比例的量的方法是解题的关键。
17.×
【分析】判断梯形的面积与高成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例,据此解答。
【详解】梯形的面积公式:面积=(上底+下底)×高÷2;
=梯形上、下底之和(一定),
(一定),比值一定,梯形的面积与高成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
18.×
【分析】根据关系式路程=速度×时间判断即可。
【详解】路程=速度×时间,汽车行驶的路程一定,即速度与时间的乘积一定,所以行驶的速度和所需要的时间成反比例;原题说法错误。
故答案为:×
【点睛】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
19.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为:所需方砖的块数×每块方砖的面积=教室的面积(一定),乘积一定,所以所需方砖的块数与每块方砖的面积成反比例;
所以:教室的面积一定,所需方砖的块数与每块方砖的面积成正比例,此说法错误。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
20.(1)48万;64万;80万;
(2)正比例;因为每天看的页数和所用的天数乘积相等;
(3)见详解;
(4)56万立方米;2.5天
【分析】(1)根据喷水天数与喷水量之间的观察完成表格;
(2)计算出表格中喷水量与喷水天数的比值,看比值是否相等;
(3)根据表格中的数据在图中描点、连线。
(4)结合图像进行计算。
【详解】(1)
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 48万 64万 80万
(2)16÷1=32÷2=48÷3=64÷4=80÷5=16(一定)
所以喷水量与喷水天数成正比例;
因为每天看的页数和所用的天数乘积相等;
(3)
(4)3.5×16=56(万立方米)
40÷16=2.5(天)
3.5天的喷水量是56万立方米;40万立方米的喷水量需要喷2.5天。
【点睛】本题考查了成正比例关系的判定、统计表及统计图的填补、从统计表或统计图中读出信息、分析数据、解决问题的能力。
21.(1)16;12;
(2)反比例关系;因为每天看的页数和所用天数的乘积相等,所以符合反比例的意义;
(3)6页
【分析】(1)根据“平均每天看的页数×所用的时间=这本故事书的总页数”直接解题即可。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
(3)用总页数÷看的天数即可。
【详解】(1)总页数:8×30=240(页)
240÷15=16(天)
240÷20=12(天)
填表如下:
平均每天看的页数/页 8 10 15 20 30
所用的时间/天 30 24 16 12 8
(2)因为每天看的页数和所用天数的乘积相等,所以符合反比例的意义。故平均每天看的页数与所用的时间成反比例;
(3)240÷40=6(页)
答:如果亮亮用40天看完了这本故事书,平均每天看6页。
【点睛】本题主要考查反比例的意义,明确平均每天看的页数×所用的时间=这本故事书的总页数是解题的关键。
22.(1)25;30
(2)成正比例;理由见详解
(3)作图见详解
(4)12.5;5.5
【分析】(1)根据单价乘数量等于总价来填表。
(2)判断两种相关联的量成什么比例,只需看它们之间的关系是商一定还是积一定,如果商一定,成正比例,如果积一定,成反比例,如果商和积都不是定量,不成比例;据此解答。
(3)先在列中找到质量数,再在行中找到对应的数量点,顺次连接。
(4)用总价、单价、质量间的关系来求总价及数量。
【详解】(1)购买香蕉的质量和应付金额如表:
质量/kg 0 1 2 3 4 5 6 ……
应付金额/元 0 5 10 15 20 25 30 ……
(2)因为=单价=5(元)(一定),所以购买香蕉的质量与应付金额成正比例。
(3)如图:
(4)5×2.5=12.5(元)
27.5÷5=5.5(千克)
购买香蕉2.5千克,应付金额12.5元,27.5元最多可以买5.5千克香蕉。
【点睛】理解两个量成正比例的意义是解决本题的关键。
23.(1)成反比例关系;利用见详解
(2)15000只
【分析】(1)根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
(2)用这批口罩的总只数除以需要的天数,即可解答。
【详解】(1)5000×24=120000(只)
6000×20=120000(只)
8000×15=120000(只)
10000×12=120000(只)
12000×10=120000(只)
所以每天生产的数量×所用时间=120000(只)(一定),每天生产的数量和所用的时间成反比例。
答:每天生产的数量与所用的时间成反比例。
(2)5000×24÷8
=120000÷8
=15000(只)
答:平均每天生产15000只口罩。
【点睛】根据正比例意义和辨识、反比例意义和辨识;以及工作量、工作时间和工作效率三者之间的关系解答问题。
24.(1)(2)见详解。
(3)480
(4)工程队修路的时间与修路的米数成正比例关系;
理由如下:因为定值,所以工程队修路的时间与修路的米数成正比例关系。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)根据表格中的数据描点连线即可;
(3)用1天修的米数乘8就是8天修的米数;
(4)工程队修路的时间与修路的米数成正比例关系。因为定值,修路的米数:时间=每天修的米数(一定),所以工程队修路的时间和修路的米数成正比例关系。
【详解】(1)如表:
修路的时间/天 0 1 2 3 4 5
修路的米数/ 0 60 120 180 240 300
(2)如图:
(3)60×8=480(米)
可以修路480米。
(4)工程队修路的时间和修路的米数成正比例关系。因为修路的米数:时间=每天修的米数(一定)。
【点睛】本题考查了正比例的意义和应用。
25.(1)见详解
(2)5小时
【分析】(1)两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)由(1)的答案可知,每小时加工零件个数与加工时间成反比例关系,这批零件的总个数是一定的,据此设如果李师傅每小时加工48个零件,需要x小时,列出比例式:48x=20×12,再根据等式的性质解答。
【详解】(1)每小时加工零件个数与加工时间成反比例关系。因为20×12=30×8=40×6=60×4=240,每小时加工零件个数与加工时间的乘积一定,所以每小时加工零件个数与加工时间成反比例关系。
(2)解:设需要x小时完成。
48x=20×12
48x=240
x=240÷48
x=5
答:需要5小时完成。
【点睛】本题考查反比例的辨认和应用。掌握反比例的意义是解题的关键。
答案第1页,共2页
一、选择题
1.已知=c(a,b均不为0),当哪个量一定时,另外两个量成正比例?( )
A.a B.b C.c D.都不是
2.龙龙制作了一个摩天轮模型,模型高度与摩天轮的实际高度之比是3∶400,现测得模型的高度为27cm,则摩天轮的实际高度是( )米。
A.27 B.33 C.36 D.42
3.下面说法错误的是( )。
A.如果a∶b=c∶d,那么a∶c=b∶d
B.将一个图形按2∶1的比放大,得到的图形与原来图形面积的比还是2∶1
C.4,5,24,30这四个数可以组成比例
D.平行四边形的面积一定,它的底和高成反比例
4.( )中的两个量不成正比例。
A.订阅某期刊的份数一定,单价和总钱数
B.一箱苹果,吃掉的个数和剩下的个数
C.长方体的底面积一定,高和体积
D.在同一个正方形中,正方形的周长和边长
5.A和B是两种相关联的量,已知A×B=7,则A和B( )。
A.成正比例 B.成反比例 C.不成比例 D.没有关系
6.能够表示a和b这两种量成正比例关系的是( )。
A.a+b=8 B.a-b=8 C.a×b=8 D.a÷b=8
二、填空题
7.表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填( );如果A和B成反比例关系,那么应填( )。
A 3 6
B 7
8.若,则与成( )比例关系;若,则与成( )比例关系。(填“正”或“反”)
9.一个三角形的面积是,它的底和高成( )比例。
10.一辆车匀速行驶,路程是s千米,时间是t小时,路程和时间的比值是( ),路程和时间成( )比例。
11.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如表。每块地砖的面积与所需地砖的数量成( )比例关系,如果每块地砖的面积是0.5m2,铺教室地面需要( )块地砖;如果铺教室地面用了150块地砖,所用地砖每块的面积是( )。
每块地砖面积/ 0.2 0.3 0.4 0.6 …
所需地砖数量/块 600 400 300 200 …
12.某工厂生产一批零件,每天生产的个数与需要的天数如下表。
每天生产的个数/个 200 300 400 500
需要的天数/天 30 20 15 12
(1)每天生产的个数与需要的天数成( )比例。(填“正”或“反”)
(2)如果该工厂每天生产250个零件,需要( )天。
13.一份稿件,甲单独打需小时,乙单独打需小时,甲和乙的工作效率比是( )。
14.学校手工社团买了一种彩带,买的长度和总价关系如图:买10米这种彩带要花( )元,200元可以买( )米。
三、判断题
15.打疫苗时,每小时打疫苗的人数一定,打疫苗的总人数与所用时间成反比例。( )
16.如果(m,n均不为0),那么m和n成正比例。( )
17.当梯形的上、下底之和一定时,梯形的面积与高不成比例。( )
18.某汽车行驶的路程一定,行驶的速度和所需要的时间成正比例。( )
19.教室的面积一定,所需方砖的块数与每块方砖的面积成正比例。( )
四、解答题
20.某喷泉的喷水量与喷水天数情况如表。
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 ( ) ( ) ( )
(1)将上表填写完整。
(2)判断喷水量与喷水天数是否成正比例,并说明理由。
(3)把喷水量与喷水天数所对应的点在图中描出来,并连线。
(4)利用图像估计一下,3.5天的喷水量是( )m3;40万m3的喷水量需要喷( )天。
21.亮亮看一本故事书,平均每天看的页数和所用的时间如表。
平均每天看的页数/页 8 10 15 20 30
所用的时间/天 30 24 8
(1)将上表补充完整。
(2)平均每天看的页数与所用的时间是不是成反比例?说明理由。
(3)如果亮亮用40天看完了这本故事书,平均每天看多少页?
22.购买香蕉的质量和应付金额如表。
质量/kg 0 1 2 3 4 5 6 …
应付金额/元 0 5 10 15 20 …
(1)把上表填写完整。
(2)判断购买香蕉的质量与应付金额是否成正比例,并说明理由。
(3)把表中质量和应付金额所对应的点描在方格纸上,再顺次连接。
(4)购买香蕉2.5千克,应付金额( )元,27.5元最多可以买( )千克香蕉。
23.为了防控疫情,某口罩生产厂要完成一批生产任务,每天生产的数量与所用的时间如表:
每天生产的数量/只 5000 6000 8000 10000 12000
所用的时间/天 24 20 15 12 10
(1)每天生产的数量和所用的时间是否成反比例?说明理由。
(2)如果要8天生产完这批口罩,平均每天要生产多少只口罩?
24.一个工程队修路的时间与修路的米数的情况如下表。
修路的时间/天 0 1 2 3 4 5
修路的米数/ 0 60 120 180
(1)将上面的表格填写完整。
(2)根据表中数据,在下图中描出修路的时间和修路的米数所对应的点,再把这些点依次连接起来。
(3)如果修8天路,可以修( )米。
(4)工程队修路的时间与修路的米数是否成正比例关系?为什么?
25.李师傅要加工一批零件,每小时加工零件个数与加工时间如下表。
每小时加工零件的个数/个 20 30 40 60 …
加工的时间/时 12 8 6 4 …
(1)每小时加工零件个数与加工时间是否成反比例关系?为什么?
(2)如果李师傅每小时加工48个零件,需要多少小时完成?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定,据此解答;
【详解】=c(a,b均不为0),c也不为0,当c一定时,b和a成正比例。
已知=c(a,b均不为0)。当c一定时,另外两个量成正比例。
故答案为:C
【点睛】熟练掌握正比例意义是解答本题的关键。
2.C
【分析】设摩天轮的实际高度是x米,根据摩天轮的实际高度与模型高度的比值是一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【详解】解:设摩天轮的实际高度是x米,由题意得:
27厘米=0.27米
0.27: x =3:400
3x=0.27×400
3x÷3=0.27×400÷3
x=108÷3
x=36
摩天轮的实际高度是36米
故答案为:C
【点睛】本题考查了正反比例应用题,关键是得出摩天轮实际高度与模型高度的比值是一定的。
3.B
【分析】根据比的基本性质:两个内项之积等于两个外项之积;
图形放大或缩小后,对应边长的比相等,周长的比相等,但面积的比不相等;
比例的意义:表示两个比相等的式子,叫做比例;
再根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此逐项分析判断解答。
【详解】A.a∶b=c∶d;所以ad=bc;即a∶c=b∶d,
原题干正确,不符合题意;
B.将一个图形按2∶1比放大,假设这个图形是正方形,得到的图形与原来图形面积的比是:
(2×2)∶(1×1)
=4∶1
原题干说法错误,符合题意;
C.因为24∶4=6;30∶5=6,所以24∶4=30∶5,
4,5,24,30这四个数可以组成比例;
原题干说法正确,不符合题意;
D.底×高=平行四边形面积(一定),底和高成反比例,原题干说法确定,不符合题意。
故答案为:B
【点睛】本题考查的知识点较多,要逐项分析进行解答。
4.B
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【详解】A.总价÷单价=数量(一定),比值一定,单价和总钱数成正比例关系。
B.一箱苹果的总个数-吃掉的个数=剩下的个数,比值和积都不一定,吃掉的个数和剩下的个数不成比例;
C.长方体的体积÷高=底面积(一定),比值一定,高和体积成正比例关系;
D.边长=周长÷4(一定),比值一定,在同一个正方形中,正方形的周长和边长成正比例关系;
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
5.B
【分析】根据数量关系判断是商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例,其他关系不成比例。
【详解】根据分析可知,A×B=7,乘积一定,故A和B成反比例。
故答案为:B
【点睛】此题主要考查学生对正、反比例判定的理解与应用。
6.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此,对选项逐一分析即可。
【详解】A.a+b=8,a和b这两种量既不是比值一定,也不是乘积一定,所以二者不成比例;
B.a-b=8,a和b这两种量既不是比值一定,也不是乘积一定,所以二者不成比例;
C.a×b=8,a和b这两种量乘积一定,等于8,所以二者成反比例;
D.a÷b=8,a和b这两种量比值一定,等于8,所以二者成正比例。
故答案为:D
【点睛】本题属于辨识正反比例的量,主要看两个量是比值一定,还是乘积一定,据此作出判断即可。
7. 14 3.5
【分析】如果A和B成正比例关系,则3与7的比等于6与方框内数的比;如果A和B成反比例关系,则3与7的积等于6与方框内数的积。
【详解】解:设方框内的数为x。
如果A和B成正比例关系,则
3:7=6:x
3x=7×6
3x÷3=42÷3
x=14
表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填14;
如果A和B成反比例关系,则
6x=3×7
6x÷6=21÷6
x=3.5
如果A和B成反比例关系,那么应填3.5。
【点睛】两种相关联的量,若其成正比例关系,则其比值一定;若其成反比例关系,则其乘积一定。
8. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此分析题目即可解答。
【详解】(一定),乘积一定,所以x与y成反比例关系;
(一定),比值一定,所以x与y成正比例关系。
【点睛】本题是一道关于正反比例的题目,可依据判断正反比例的方法求解。
9.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】三角形的底高面积
因为三角形的面积为
所以三角形的底高(一定),三角形的底和高乘积一定,所以底和高成反比例。
【点睛】掌握正反比例的意义是解答此题的关键。
10. 正
【分析】根据速度=路程÷时间,可知路程和时间的比值是速度,比值一定时,路程和时间成正比例,据此解答即可。
【详解】由分析可知;一辆车匀速行驶,路程是s千米,时间是t小时,路程和时间的比值是,路程和时间成正比例。
【点睛】根据路程、时间、速度的关系和正比例的判定方法,解答此题即可。
11. 反 240 0.8
【分析】判断两个相关联的量之间成什么比例,就看这两种量对应的是比值一定,还剩乘积一定,如果是比值一定,就成正比例;如果乘积一定,就成反比例;用每块地砖的面积与所需地砖的数量的乘积除以每块地砖的面积,求出需要地砖的块数;用每块地砖的面与所需地砖的数量的乘积除以地砖的块数,求出每块地砖的面积,据此解答。
【详解】0.2×600=0.3×400=0.4×300=0.6×200=120(一定);乘积一定,每块地砖的面积与所需地砖的数量成反比例;
120÷0.5=240(块)
120÷150=0.8(平方米)
【点睛】根据正比例意义和辨识,反比例意义和辨识进行解答。
12.(1)反
(2)24
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)用零件总个数÷每天生产的个数=需要天数,代入数据,即可解答。
(1)
200×30=300×20=400×15=500×12=6000(个),每天生产的个数与需要的天数乘积一定,所以每天生产的个数与需要的天数成反比例。
(2)
200×30÷250
=6000÷250
=24(天)
【点睛】根据正比例意义以及辨别和反比例意义以及辨别进行解答。
13.6∶5
【分析】根据工作量=工作效率×工作时间,可得工作量一定时,工作效率和工作时间成反比例,据此解答即可。
【详解】因为工作量一定,都是一份稿件,所以甲和乙工作效率比是:∶=6∶5
【点睛】解答此题的关键是要明确:工作量一定时,工作效率和工作时间成反比例。
14. 80 25
【分析】从图中可以看出总价和买的长度成正比例关系,8元对应的是1米,所以每米需要8元,那么10米就需要(8×10)元,200可以买(200÷8)米。
【详解】8×10=80(元)
200÷8=25(米)
所以买10米这种彩带要花80元,200元可以买25米。
【点睛】此题考查了学生对正比例关系的辨识及应用。
15.×
【分析】根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
【详解】打疫苗的总人数÷打疫苗所用的时间=每小时打疫苗的人数(一定),打疫苗的总人数与所用时间成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
16.×
【分析】根据比例的基本性质:两个内项之积等两个于外项之积;写出这个比例式mn=2×3,即mn=6;再根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此判断解答。
【详解】=(m,n均不为0),
mn=2×3,即mn=6(一定),m和n成反比例。
原题干说法错误。
故答案为:×
【点睛】掌握比例的基本性质和辨识成正、反比例的量的方法是解题的关键。
17.×
【分析】判断梯形的面积与高成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例,据此解答。
【详解】梯形的面积公式:面积=(上底+下底)×高÷2;
=梯形上、下底之和(一定),
(一定),比值一定,梯形的面积与高成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
18.×
【分析】根据关系式路程=速度×时间判断即可。
【详解】路程=速度×时间,汽车行驶的路程一定,即速度与时间的乘积一定,所以行驶的速度和所需要的时间成反比例;原题说法错误。
故答案为:×
【点睛】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
19.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为:所需方砖的块数×每块方砖的面积=教室的面积(一定),乘积一定,所以所需方砖的块数与每块方砖的面积成反比例;
所以:教室的面积一定,所需方砖的块数与每块方砖的面积成正比例,此说法错误。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
20.(1)48万;64万;80万;
(2)正比例;因为每天看的页数和所用的天数乘积相等;
(3)见详解;
(4)56万立方米;2.5天
【分析】(1)根据喷水天数与喷水量之间的观察完成表格;
(2)计算出表格中喷水量与喷水天数的比值,看比值是否相等;
(3)根据表格中的数据在图中描点、连线。
(4)结合图像进行计算。
【详解】(1)
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 48万 64万 80万
(2)16÷1=32÷2=48÷3=64÷4=80÷5=16(一定)
所以喷水量与喷水天数成正比例;
因为每天看的页数和所用的天数乘积相等;
(3)
(4)3.5×16=56(万立方米)
40÷16=2.5(天)
3.5天的喷水量是56万立方米;40万立方米的喷水量需要喷2.5天。
【点睛】本题考查了成正比例关系的判定、统计表及统计图的填补、从统计表或统计图中读出信息、分析数据、解决问题的能力。
21.(1)16;12;
(2)反比例关系;因为每天看的页数和所用天数的乘积相等,所以符合反比例的意义;
(3)6页
【分析】(1)根据“平均每天看的页数×所用的时间=这本故事书的总页数”直接解题即可。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
(3)用总页数÷看的天数即可。
【详解】(1)总页数:8×30=240(页)
240÷15=16(天)
240÷20=12(天)
填表如下:
平均每天看的页数/页 8 10 15 20 30
所用的时间/天 30 24 16 12 8
(2)因为每天看的页数和所用天数的乘积相等,所以符合反比例的意义。故平均每天看的页数与所用的时间成反比例;
(3)240÷40=6(页)
答:如果亮亮用40天看完了这本故事书,平均每天看6页。
【点睛】本题主要考查反比例的意义,明确平均每天看的页数×所用的时间=这本故事书的总页数是解题的关键。
22.(1)25;30
(2)成正比例;理由见详解
(3)作图见详解
(4)12.5;5.5
【分析】(1)根据单价乘数量等于总价来填表。
(2)判断两种相关联的量成什么比例,只需看它们之间的关系是商一定还是积一定,如果商一定,成正比例,如果积一定,成反比例,如果商和积都不是定量,不成比例;据此解答。
(3)先在列中找到质量数,再在行中找到对应的数量点,顺次连接。
(4)用总价、单价、质量间的关系来求总价及数量。
【详解】(1)购买香蕉的质量和应付金额如表:
质量/kg 0 1 2 3 4 5 6 ……
应付金额/元 0 5 10 15 20 25 30 ……
(2)因为=单价=5(元)(一定),所以购买香蕉的质量与应付金额成正比例。
(3)如图:
(4)5×2.5=12.5(元)
27.5÷5=5.5(千克)
购买香蕉2.5千克,应付金额12.5元,27.5元最多可以买5.5千克香蕉。
【点睛】理解两个量成正比例的意义是解决本题的关键。
23.(1)成反比例关系;利用见详解
(2)15000只
【分析】(1)根据正比例、反比例的判断方法:判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。据此解答。
(2)用这批口罩的总只数除以需要的天数,即可解答。
【详解】(1)5000×24=120000(只)
6000×20=120000(只)
8000×15=120000(只)
10000×12=120000(只)
12000×10=120000(只)
所以每天生产的数量×所用时间=120000(只)(一定),每天生产的数量和所用的时间成反比例。
答:每天生产的数量与所用的时间成反比例。
(2)5000×24÷8
=120000÷8
=15000(只)
答:平均每天生产15000只口罩。
【点睛】根据正比例意义和辨识、反比例意义和辨识;以及工作量、工作时间和工作效率三者之间的关系解答问题。
24.(1)(2)见详解。
(3)480
(4)工程队修路的时间与修路的米数成正比例关系;
理由如下:因为定值,所以工程队修路的时间与修路的米数成正比例关系。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)根据表格中的数据描点连线即可;
(3)用1天修的米数乘8就是8天修的米数;
(4)工程队修路的时间与修路的米数成正比例关系。因为定值,修路的米数:时间=每天修的米数(一定),所以工程队修路的时间和修路的米数成正比例关系。
【详解】(1)如表:
修路的时间/天 0 1 2 3 4 5
修路的米数/ 0 60 120 180 240 300
(2)如图:
(3)60×8=480(米)
可以修路480米。
(4)工程队修路的时间和修路的米数成正比例关系。因为修路的米数:时间=每天修的米数(一定)。
【点睛】本题考查了正比例的意义和应用。
25.(1)见详解
(2)5小时
【分析】(1)两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)由(1)的答案可知,每小时加工零件个数与加工时间成反比例关系,这批零件的总个数是一定的,据此设如果李师傅每小时加工48个零件,需要x小时,列出比例式:48x=20×12,再根据等式的性质解答。
【详解】(1)每小时加工零件个数与加工时间成反比例关系。因为20×12=30×8=40×6=60×4=240,每小时加工零件个数与加工时间的乘积一定,所以每小时加工零件个数与加工时间成反比例关系。
(2)解:设需要x小时完成。
48x=20×12
48x=240
x=240÷48
x=5
答:需要5小时完成。
【点睛】本题考查反比例的辨认和应用。掌握反比例的意义是解题的关键。
答案第1页,共2页
