第三单元 解决问题的策略(培优卷)-六年级数学下册高频易错题必刷卷(苏教版)(含答案)
文档属性
| 名称 | 第三单元 解决问题的策略(培优卷)-六年级数学下册高频易错题必刷卷(苏教版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 12:06:18 | ||
图片预览




文档简介
第三单元 解决问题的策略(培优卷)
六年级数学下册高频易错题必刷卷
题型 一 二 三 四 五 总分
分数
注意:请认真审题,做到书写端正,格式正确,卷面整洁。
一、选择题(每题2分,共16分)
1.“鸡兔同笼”问题是我国古代的数学名题之一。书中题目是这样的:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?它出自唐代的( )。
A.《九章算术》 B.《孙子算经》 C.《周髀算经》
2.有三个游行方阵,每个方阵80人,第一方阵有是男生,第二方阵的女生和第三方阵的男生一样多。这三个方阵中一共有男生( )人。
A.100 B.140 C.240
3.有A、B、C三个数字,已知,,且A比C少2,那么B是( )。
A.20 B.30 C.40
4.水结成冰,体积约增加;那么冰化成水,体积约减少( )。
A. B. C.
5.学校举行数学竞赛,共有10道题,每答对1道题得8分,每答错1道题倒扣5分,小明最终得了41分,他答对了( )道题。
A.5 B.6 C.7
6.如果从甲车间调的工人到乙车间,则甲乙两车间人数相等,原来甲车间人数比乙车间人数多( )。
A.10% B.20% C.25%
7.根据线段图所示的关系,求喜欢足球的学生人数的正确列式是( )。
A.120× B.120÷ C.120×
8.一本故事书已看的页数和未看页数的比是2∶3,下面说法错误的是( )。
A.已看的页数是未看页数的 B.已看的页数比未看的页数少
C.已看了全书页数的
二、填空题(每题2分,共16分)
9.阳光小学组织安全意识知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分,弃权不扣也不加。芳芳小组弃权两道,得了120分,他们答对了( )题。
10.笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。下面说法正确的有______。(填序号)
①鸡兔一共有35只。
②假如全是鸡,就会少24只脚。
③假如全是兔,就会多24只脚。
④如果它们都抬起2只脚,剩下站在地上的24只脚就都是兔子的。
11.王月的储蓄罐里有1角和5角的硬币共35枚,一共是11.5元,则5角硬币有( )枚。
12.学校食堂运来一批大米,用了几个星期后,已经用去了,剩下的与用去的比是( ),如果用去的比剩下的少600千克,则还剩( )千克。
13.故事书与科技书本数比是7∶3,已知故事书比科技书多56本,故事书有________本。
14.金陵小学六年级有三个班,每班都是50人。其中一班女生占一班总人数的,二班女生与三班男生一样多。这个学校六年级女生有( )人。
15.妈妈给优乐买了一套衣服共300元,裤子的价钱比上衣少,上衣( )元,裤子( )元。
16.有一首民谣:“一队猎手一队狗,二队并着一起走,数头一共三百六,数腿一共八百九。”民谣中有( )个猎手,( )只狗。
三、判断题(每题2分,共8分)
17.圆柱体积是圆锥体积的3倍,这两者一定是等底等高。( )
18.盐和水的质量比是,盐占盐水的。( )
19.周长相等的长方形面积不一定相等,周长相等的正方形面积一定相等。( )
20.红花的朵数比蓝花多,蓝花的朵数就比红花少。( )
四、计算题(共12分)
21.(6分)看图列方程,不解答。
22.(6分)看图列式或方程计算。
五、解答题(共48分)
23.(6分)六(2)班男生人数占总人数的,女生有25人,男生有多少人?(先把线段图补充完整,再列式解答。)
24.(6分)六年二班46人去公园划船,共乘12只船。其中大船每只坐5人,小船每只坐3人,大船和小船各有多少只?
25.(6分)皓午看一本小说,看了3天后他发现已经看的页数与还剩的页数比是,如果再看25页就正好看了一半,这本书有多少页?
26.(6分)刘大伯家将3680平方米的菜地分成四块分别种辣椒、黄瓜、茄子和西红柿。已知辣椒地的面积是800平方米,黄瓜地的面积比西红柿多120平方米,茄子地的面积比西红柿少150平方米。黄瓜、茄子和西红柿菜地的面积各是多少平方米?
27.(6分)一根木头,不知它的长度,用一根绳子来量,绳子多1.6米,如果将绳子对折后再来量,绳子又短0.6米,这根木头长多少米?
28.(6分)一项工作,甲独做10天完成,乙独做5天只能完成全部任务的,现在两人合作几天才能完成全部工作?
29.(6分)牧场上有一片青草,每天都生长得一样快,这片青草供给10头牛吃,可以吃22天,或者提供给16头牛吃,可以吃10天,如果供给27头牛吃,可以吃几天?
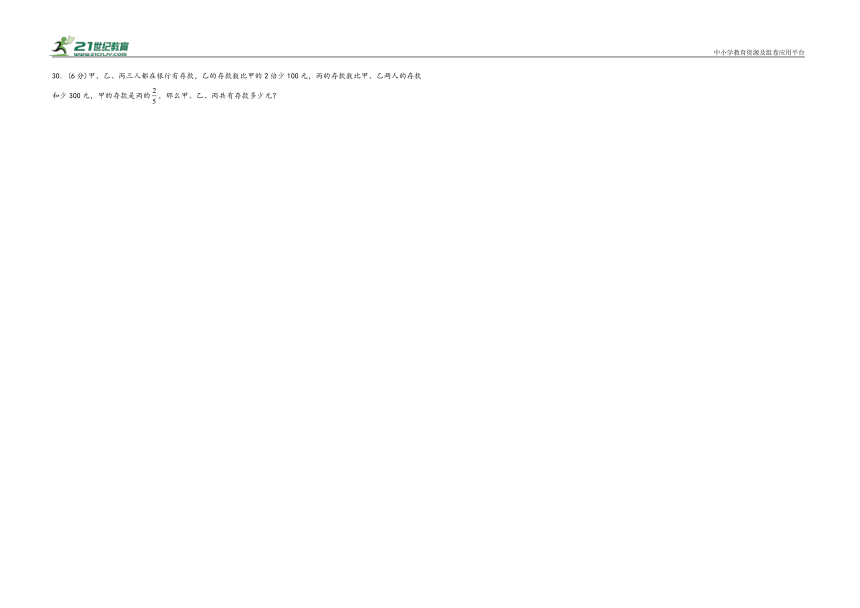
30.(6分)甲、乙、丙三人都在银行有存款,乙的存款数比甲的2倍少100元,丙的存款数比甲、乙两人的存款和少300元,甲的存款是丙的,那么甲、乙、丙共有存款多少元?
参考答案
1.B
【解析】鸡兔同笼问题最早见于我国的《孙子算经》,据此做出选择。
【详解】鸡兔同笼问题出自《孙子算经》;
故答案选:B。
【点睛】鸡兔同笼问题是一个古老的数学问题,有兴趣的同学可以了解一下数学发展史。
2.A
【分析】第二方阵的女生和第三方阵的男生一样多,则第二方阵和第三方阵男女生同样多,均为80人;再将第一方阵的人数看成单位“1”,用乘法求出第一方阵的就是第一方阵男生人数,最后加上第二方阵和第三方阵男生总人数(80人)即可。
【详解】80×+80
=20+80
=100(人)
这三个方阵中一共有男生100人。
故答案为:A
【点睛】理解“第二方阵的女生和第三方阵的男生一样多”是解题的关键。
3.C
【分析】因为A∶B=3∶4,B∶C=5∶4,把3∶4的前、后项都乘5,5∶4的前、后项都乘4,A、B、C写成连比的形式,求出1份是多少,再根据B所占的份数即可求出B。
【详解】A∶B=3∶4
=(3×5)∶(4×5)
=15∶20
B∶C=5∶4
=(5×4)∶(4×4)
=20∶16
A∶B∶C=15∶20∶16
即A为15份,B为20份,C为16份
C比A大16-15=1(分)
A比C少2,即1份是2;
B=20×2=40
有A、B、C三个数字,已知,,且A比C少2,那么B是40。
故答案为:C
【点睛】此题是考查比的应用,关键是把两个比写成连比的形式,求出A、B、C所占的份数,求出1份是多少,进而求出B。
4.C
【分析】根据题意,水结成冰,体积约增加,是把水的体积看作单位“1”,冰的体积是水的(1+);求冰化成水,体积约减少几分之几,就是求水的体积比冰的体积减少几分之几,用水和冰的体积之差除以冰的体积即可。
【详解】÷(1+)
=÷
=×
=
故答案为:C
【点睛】找准单位“1”,明确求一个数比另一个数多或少几分之几,用两者的差值除以另一个数。
5.C
【分析】先假设全部做对,求出总分,肯定会多少一些,然后求出总分相差多少,用总差除以每错看一题的分差,求出做错的数量,再计算做对的数量。
【详解】8×10=80(分)
80-41=39(分)
答错的题目:
39÷(8+5)
=39÷13
=3(道)
答对的题目:
10-3=7(道)
【点睛】本题考查的是鸡兔同笼问题,注意在这里答错和答对之间相差的是13分,而不是7分。
6.C
【分析】根据“从甲车间调的工人到乙车间”将甲车间人数看成10份,调出1份到乙车间后剩下10-1=9份,即此时乙车间是9份,由此可知乙车间原来是9-1=8份。求原来甲车间人数比乙车间人数多百分之几,用原来的份数差÷乙原来的份数即可。
【详解】将甲车间人数看成10份,则乙车间原来是10-1-1=8份
原来甲车间人数比乙车间人数多:(10-8)÷8
=2÷8
=25%
故答案为:C
【点睛】解答此类问题时,将分数转化为份数可以快速解题。
7.B
【分析】根据图意可知,喜欢篮球的人数比喜欢足球的人数少,喜欢篮球的人数占喜欢足球的人数的,具体数量÷具体数量对应的分率=单位1,据此解答。
【详解】喜欢足球的学生人数=120÷(1-)。
故答案为:B。
【点睛】读懂图示、明确具体量÷对应分率=单位1是解答本题的关键。
8.B
【分析】已看的页数和未看页数的比是2∶3,把已看的页数看作2份,为看的页数看作3份,再判断每个选项的说法正确与否即可。
【详解】已看的页数是未看页数、已看了全书页数的、全书还有没有看三种说法都正确;
(3-2)÷3=,即已看的页数比未看的页数少,因此,已看的页数比未看的页数少说法不正确;
故选:B。
【点睛】本题考查比的意义,解答本题的关键是掌握比的概念。
9.14
【分析】根据“每做对一道得10分,答错扣5分,”可知:答错一题比答对一题少得10+5=15分;假设芳芳小组全部答对得分是10×18=180(分),比120分多得180-120=60(分),那么他们答错了:60÷(10+5)=4(道);所以芳芳小组答对:18-4=14道题。
【详解】[10×(20-2)-120]÷(10+5)
=[10×18-120]÷15
=[180-120]÷15
=60÷15
=4(道)
20-2-4
=18-4
=14(道)
【点睛】鸡兔同笼问题一般利用解设法解答,本题先假设全部答对,得出与实际得分的差就是每道错题对应的失分,从而求出错题数。
10.①②④
【分析】根据题意,结合解答鸡兔同笼问题的方法逐项判断即可。鸡有两只脚,兔子有四只脚,假设笼中全都是鸡或者兔,根据头数(即动物的个数)求出假设时的腿数,再把假设时的腿数与实际情况相比较即可。
【详解】①因为有35个头,则鸡兔一共有35只;说法正确。
②假如全是鸡,共有35×2=70(只)脚,就会少94-70=24(只)脚;说法正确。
③假如全是兔,共有35×4=140(只)脚,就会多140-94=46(只)脚;说法错误。
④如果它们都抬起2只脚,剩下站在地上的脚有:94-35×2=24(只),即24只脚就都是兔子的;说法正确。
综上所述,说法正确的有①②④。
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
11.20
【分析】先把11.5元换成以角为单位的数,即11.5元=115角,假设全是1角钱,由于硬币一共有35枚,则相当于35枚1角的,即35×1=35(角),由于实际有115角,还差了115-35=80(角),这个时候把1角的换成5角的,把一枚1角的换成5角的相当于比原来增加了5-1=4(角),总共差了80角,即80÷4=20(枚),需要把20枚1角钱换成5角的即可。
【详解】假设35枚硬币全是1角的。
11.5元=115角
1×35=35(角)
115-35=80(角)
80÷(5-1)
=80÷4
=20(枚)
【点睛】本题主要考查鸡兔同笼,鸡兔同笼可以利用假设法,或者方程的方法解决。熟练掌握假设法解决应用题并灵活运用。
12. 3∶2 1800
【分析】将这批大米看成单位“1”,用去,还剩下1-=;求剩下的与用去的比,用剩下的分率∶用去的分率即可;用去的比剩下的少-=,是600千克,根据分数除法的意义,用600÷求出大米的质量。再根据分数乘法的意义,用600÷×求出剩下的质量。
【详解】(1-)∶=3∶2
600÷(1--)×
=600÷×
=3000×
=1800(千克)
【点睛】本题主要考查比的意义及“已知一个数的几分之几是多少,求这个数”的实际应用。
13.98
【分析】用故事书比科技书多的本数除以多的份数求出每份是多少,然后用每份数乘故事书的份数即可求出故事书的本数。
【详解】56÷(7-3)×7
=56÷4×7
=14×7
=98(本)
【点睛】此题考查比的应用,熟练掌握总数量÷对应份数=1份量是解题的关键。
14.80
【分析】二班女生与三班男生一样多,这两个班的人数放在一起,男生和女生就各是50人,只要求出一班的女生人数,问题就解决了。一班女生占一班总人数的,据此可以求一班的女生人数;据此解答。
【详解】50+50×
=50+30
=80(人)
【点睛】解决这道题的关键是根据二班女生与三班男生一样多,利用转化的思想,来找出二班和三班的女生人数和相当于一个班的人数。
15. 220 80
【分析】由题意可知:裤子的价钱是上衣的1-=,一套衣服的价钱是上衣的1+,是300元。据此求出上衣的价钱,再用上衣的价钱×即是裤子的价钱。
【详解】300÷(1-+1)
=300÷
=220(元)
220×(1-)
=220×
=80(元)
答:上衣220元,裤子80元。
故答案为:220;80
【点睛】本题主要考查分数四则复合应用题,解题的关键是找出与已知数量对应的分率。
16. 275 85
【分析】假设360个全是猎手,则腿一共有:360×2=720(条),比实际少:890-720=170(条),因为一个猎手比一条狗少2条腿,所以少的是狗的腿的数量,所以狗有:170÷2=85(条),则人有:360-85=275(人),据此解答即可。
【详解】解:假设360个全是猎手,则狗有:
(890-360×2)÷2
=170÷2
=85(条)
猎手有:360-85=275(人)
有275个猎手,85条狗。
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
17.×
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,反过来不一定成立,举例说明即可。
【详解】圆柱体积30立方米,圆锥体积10立方米,30=15×2=6×5,圆柱底面积可以是15平方米,高是2米,圆锥底面积可以是6平方米,高是5米,不一定等底等高,所以原题说法错误。
故答案为:×
【点睛】关键是理解等底等高的圆柱和圆锥体积之间的关系。
18.×
【分析】盐水是由盐和水组成,题中盐为1份,水是20份,则盐水为21份,所以盐占盐水的,据此进行判断。
【详解】
5%=
故答案为:×
【点睛】理解盐水是由盐和水组成的是解答本题的关键。
19.√
【分析】长方形的周长=(长+宽)×2,长方形的面积=长×宽,周长相等的长方形面积不一定相等;正方形的边长=正方形的周长÷4,因为正方形的周长相等,所以边长也相等,根据正方形的面积计算公式可知,边长相等的正方形,面积一定相等,据此解题。
【详解】周长相等的长方形面积不一定相等,周长相等的正方形面积一定相等。
所以原题说法正确。
【点睛】此题主要考查了学生对长方形和正方形周长面积之间的关系,需要牢记长方形和正方形的面积和周长公式。
20.×
【分析】根据题意可知,前者单位“1”是甲,后者单位“1”是乙,求甲比乙多几分之几,就是(甲-乙)÷乙,而反过来求乙比甲少几分之几,就是(甲-乙)÷甲,由此可以解答。
【详解】红花的朵数比蓝花多几分之几,列式为(红花-蓝花)÷蓝花,而蓝花的朵数比红花少几分之几,列式为(红花-蓝花)÷红花,可以看出除数不一样,得数也不一样。
所以原题说法错误。
【点睛】此题主要考查学生对分数除法的理解,比后面是几就除以几。
21.x+3x=9.6
【分析】观察线段图可知,圆珠笔的价格为x元,钢笔价格是圆珠笔的3倍,即为3x元,钢笔和圆珠笔的总价格为9.6元,据此列方程求解即可。
【详解】解:设圆珠笔的价格为x元,则钢笔的价格是3x元。
x+3x=9.6
4x=9.6
4x÷4=9.6÷4
x=2.4
圆珠笔的单价为2.4元。
【点睛】找出圆珠笔价格x元,钢笔价格3x元,与总价格9.6之间的数量关系是解答此题的关键。
22.篮球有25个
【分析】由图意知:以篮球数量为单位“1”,设篮球有x个,足球的数量相当于篮球的,即,两种球的数量和是40个,即,解此方程即可。
【详解】解:设篮球有x个,足球的有x个。
23.图见详解;20人
【分析】将总人数单位单位“1”,平均分成9份,则男生占4份,女生占9-4=5份。已知女生人数为25人,用女生人数÷求出总人数,总人数×即可求出男生人数;据此解答。
【详解】画图如下:
25÷(1-)×
=25÷×
=25××
=45×
=20(人)
答:男生有20人。
【点睛】本题考查已知一个数的几分之几是多少求这个数及求一个数的几分之几是多少的综合运用。
24.大船5只;小船7只
【分析】设大船x只,则小船有(12-x)只,根据大船数量×每船坐的人数+小船数量×每船坐的人数=总人数,列出方程求出x的值是大船数量,总数量-大船数量=小船数量,据此列式解答。
【详解】解:设大船x只。
5x+(12-x)×3=46
5x+36-3x=46
2x+36-36=46-36
2x÷2=10÷2
x=5
12-5=7(只)
答:大船有5只,小船有7只。
【点睛】用方程解决问题的关键是找到等量关系。
25.450页
【分析】把这本书的页数看作单位“1”,已经看的页数为4份,还剩的页数为5份。已经看的占总页数的。求出25页所占的分率,再用分数除法解题即可。
【详解】
=
=25×18
=450(页)
答:这本书有450页。
【点睛】本题主要考查分数除法的意义。求出25页所占的分率是解题的关键。
26.黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米
【分析】用3680减去辣椒地的面积就是黄瓜、茄子和西红柿的面积和,用黄瓜、茄子和西红柿的面积和减去黄瓜地的面积比西红柿多的120平方米,再加上茄子地的面积比西红柿少的150平方米,就相当于3块西红柿地的面积,再除以3就是1块西红柿地的面积,进一步求出黄瓜地和茄子地的面积。
【详解】3680﹣800=2880(平方米)
(2880﹣120+150)÷3
=2910÷3
=970(平方米)
970+120=1090(平方米)
970﹣150=820(平方米)
答:黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米。
【点睛】解决此题的关键是求出西红柿地的面积。
27.2.8米
【分析】要求木头的长度,先要求出绳子的长度,根据题意,绳子的长度-1.6米=木头的长度,而木头的长度又等于绳子的长度÷2+0.6,所以绳子的长度-1.6米=绳子的长度÷2+0.6,然后列方程解答即可。
【详解】解:设绳子的长度是x米。
x-1.6=x÷2+0.6
x=0.6+1.6
x=2.2÷
x=4.4
4.4-1.6=2.8(米)
答:这根木头长2.8米。
【点睛】本题主要考查列方程解含有两个未知数的问题,解题的关键是找出等量关系式并列出方程。
28.6天
【分析】甲独做10天完成,则甲每天完成这项工作的1÷10=;乙独做5天只能完成全部任务的,则乙每天完成这项工作的÷5=;甲、乙合作一天完成这项工作的+=,两人合作完成全部工作需要1÷=6天;据此解答。
【详解】1÷(1÷10+÷5)
=1÷(+)
=1÷
=6(天)
答:现在两人合作6天才能完成全部工作。
【点睛】本题考查简单的工程问题,解题的关键是求出甲乙工作效率之和。
29.5天
【分析】假设每头牛每天吃青草1份,先求出青草的增加的速度:(22×10-16×10)÷(22-10)=5(份);然后求出草场原有的草的份数:22×10-5×22=110(份);那么27头牛每天吃青草27份,青草每天增加5份,可以看作每天有22头牛在吃草,草场原有的110份的草,可吃,110÷22=5(天)。
【详解】假设每头牛每天吃青草1份,
青草增加的速度:
(22×10-16×10)÷(22-10)
=60÷12
=5(份);
原有的草的份数:
22×10-5×22
=220-110
=110(份);
可供27头牛吃:
110÷(27-5)
=110÷22
=5(天);
答:这个草场的草可供27头牛吃5天。
【点睛】本题考查了牛吃草的问题,关键的是求出青草的每天增加的速度(份数)和草场原有的草的份数。
30.4300元
【解析】设甲的存款为未知数,然后表示出乙的存款,根据甲、乙两人的存款和表示出丙的存款,再根据甲和丙的关系表示出丙的存款,据此列方程求解。
【详解】解:设甲存款为x元;
乙的存款:
丙的存款:
丙的存款:
(元)
答:甲、乙、丙共有存款4300元。
中小学教育资源及组卷应用平台
【点睛】列方程求解应用题的时候,关键是合理设未知数,并准确找出等量关系,然后列方程求解。
六年级数学下册高频易错题必刷卷
题型 一 二 三 四 五 总分
分数
注意:请认真审题,做到书写端正,格式正确,卷面整洁。
一、选择题(每题2分,共16分)
1.“鸡兔同笼”问题是我国古代的数学名题之一。书中题目是这样的:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?它出自唐代的( )。
A.《九章算术》 B.《孙子算经》 C.《周髀算经》
2.有三个游行方阵,每个方阵80人,第一方阵有是男生,第二方阵的女生和第三方阵的男生一样多。这三个方阵中一共有男生( )人。
A.100 B.140 C.240
3.有A、B、C三个数字,已知,,且A比C少2,那么B是( )。
A.20 B.30 C.40
4.水结成冰,体积约增加;那么冰化成水,体积约减少( )。
A. B. C.
5.学校举行数学竞赛,共有10道题,每答对1道题得8分,每答错1道题倒扣5分,小明最终得了41分,他答对了( )道题。
A.5 B.6 C.7
6.如果从甲车间调的工人到乙车间,则甲乙两车间人数相等,原来甲车间人数比乙车间人数多( )。
A.10% B.20% C.25%
7.根据线段图所示的关系,求喜欢足球的学生人数的正确列式是( )。
A.120× B.120÷ C.120×
8.一本故事书已看的页数和未看页数的比是2∶3,下面说法错误的是( )。
A.已看的页数是未看页数的 B.已看的页数比未看的页数少
C.已看了全书页数的
二、填空题(每题2分,共16分)
9.阳光小学组织安全意识知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分,弃权不扣也不加。芳芳小组弃权两道,得了120分,他们答对了( )题。
10.笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。下面说法正确的有______。(填序号)
①鸡兔一共有35只。
②假如全是鸡,就会少24只脚。
③假如全是兔,就会多24只脚。
④如果它们都抬起2只脚,剩下站在地上的24只脚就都是兔子的。
11.王月的储蓄罐里有1角和5角的硬币共35枚,一共是11.5元,则5角硬币有( )枚。
12.学校食堂运来一批大米,用了几个星期后,已经用去了,剩下的与用去的比是( ),如果用去的比剩下的少600千克,则还剩( )千克。
13.故事书与科技书本数比是7∶3,已知故事书比科技书多56本,故事书有________本。
14.金陵小学六年级有三个班,每班都是50人。其中一班女生占一班总人数的,二班女生与三班男生一样多。这个学校六年级女生有( )人。
15.妈妈给优乐买了一套衣服共300元,裤子的价钱比上衣少,上衣( )元,裤子( )元。
16.有一首民谣:“一队猎手一队狗,二队并着一起走,数头一共三百六,数腿一共八百九。”民谣中有( )个猎手,( )只狗。
三、判断题(每题2分,共8分)
17.圆柱体积是圆锥体积的3倍,这两者一定是等底等高。( )
18.盐和水的质量比是,盐占盐水的。( )
19.周长相等的长方形面积不一定相等,周长相等的正方形面积一定相等。( )
20.红花的朵数比蓝花多,蓝花的朵数就比红花少。( )
四、计算题(共12分)
21.(6分)看图列方程,不解答。
22.(6分)看图列式或方程计算。
五、解答题(共48分)
23.(6分)六(2)班男生人数占总人数的,女生有25人,男生有多少人?(先把线段图补充完整,再列式解答。)
24.(6分)六年二班46人去公园划船,共乘12只船。其中大船每只坐5人,小船每只坐3人,大船和小船各有多少只?
25.(6分)皓午看一本小说,看了3天后他发现已经看的页数与还剩的页数比是,如果再看25页就正好看了一半,这本书有多少页?
26.(6分)刘大伯家将3680平方米的菜地分成四块分别种辣椒、黄瓜、茄子和西红柿。已知辣椒地的面积是800平方米,黄瓜地的面积比西红柿多120平方米,茄子地的面积比西红柿少150平方米。黄瓜、茄子和西红柿菜地的面积各是多少平方米?
27.(6分)一根木头,不知它的长度,用一根绳子来量,绳子多1.6米,如果将绳子对折后再来量,绳子又短0.6米,这根木头长多少米?
28.(6分)一项工作,甲独做10天完成,乙独做5天只能完成全部任务的,现在两人合作几天才能完成全部工作?
29.(6分)牧场上有一片青草,每天都生长得一样快,这片青草供给10头牛吃,可以吃22天,或者提供给16头牛吃,可以吃10天,如果供给27头牛吃,可以吃几天?
30.(6分)甲、乙、丙三人都在银行有存款,乙的存款数比甲的2倍少100元,丙的存款数比甲、乙两人的存款和少300元,甲的存款是丙的,那么甲、乙、丙共有存款多少元?
参考答案
1.B
【解析】鸡兔同笼问题最早见于我国的《孙子算经》,据此做出选择。
【详解】鸡兔同笼问题出自《孙子算经》;
故答案选:B。
【点睛】鸡兔同笼问题是一个古老的数学问题,有兴趣的同学可以了解一下数学发展史。
2.A
【分析】第二方阵的女生和第三方阵的男生一样多,则第二方阵和第三方阵男女生同样多,均为80人;再将第一方阵的人数看成单位“1”,用乘法求出第一方阵的就是第一方阵男生人数,最后加上第二方阵和第三方阵男生总人数(80人)即可。
【详解】80×+80
=20+80
=100(人)
这三个方阵中一共有男生100人。
故答案为:A
【点睛】理解“第二方阵的女生和第三方阵的男生一样多”是解题的关键。
3.C
【分析】因为A∶B=3∶4,B∶C=5∶4,把3∶4的前、后项都乘5,5∶4的前、后项都乘4,A、B、C写成连比的形式,求出1份是多少,再根据B所占的份数即可求出B。
【详解】A∶B=3∶4
=(3×5)∶(4×5)
=15∶20
B∶C=5∶4
=(5×4)∶(4×4)
=20∶16
A∶B∶C=15∶20∶16
即A为15份,B为20份,C为16份
C比A大16-15=1(分)
A比C少2,即1份是2;
B=20×2=40
有A、B、C三个数字,已知,,且A比C少2,那么B是40。
故答案为:C
【点睛】此题是考查比的应用,关键是把两个比写成连比的形式,求出A、B、C所占的份数,求出1份是多少,进而求出B。
4.C
【分析】根据题意,水结成冰,体积约增加,是把水的体积看作单位“1”,冰的体积是水的(1+);求冰化成水,体积约减少几分之几,就是求水的体积比冰的体积减少几分之几,用水和冰的体积之差除以冰的体积即可。
【详解】÷(1+)
=÷
=×
=
故答案为:C
【点睛】找准单位“1”,明确求一个数比另一个数多或少几分之几,用两者的差值除以另一个数。
5.C
【分析】先假设全部做对,求出总分,肯定会多少一些,然后求出总分相差多少,用总差除以每错看一题的分差,求出做错的数量,再计算做对的数量。
【详解】8×10=80(分)
80-41=39(分)
答错的题目:
39÷(8+5)
=39÷13
=3(道)
答对的题目:
10-3=7(道)
【点睛】本题考查的是鸡兔同笼问题,注意在这里答错和答对之间相差的是13分,而不是7分。
6.C
【分析】根据“从甲车间调的工人到乙车间”将甲车间人数看成10份,调出1份到乙车间后剩下10-1=9份,即此时乙车间是9份,由此可知乙车间原来是9-1=8份。求原来甲车间人数比乙车间人数多百分之几,用原来的份数差÷乙原来的份数即可。
【详解】将甲车间人数看成10份,则乙车间原来是10-1-1=8份
原来甲车间人数比乙车间人数多:(10-8)÷8
=2÷8
=25%
故答案为:C
【点睛】解答此类问题时,将分数转化为份数可以快速解题。
7.B
【分析】根据图意可知,喜欢篮球的人数比喜欢足球的人数少,喜欢篮球的人数占喜欢足球的人数的,具体数量÷具体数量对应的分率=单位1,据此解答。
【详解】喜欢足球的学生人数=120÷(1-)。
故答案为:B。
【点睛】读懂图示、明确具体量÷对应分率=单位1是解答本题的关键。
8.B
【分析】已看的页数和未看页数的比是2∶3,把已看的页数看作2份,为看的页数看作3份,再判断每个选项的说法正确与否即可。
【详解】已看的页数是未看页数、已看了全书页数的、全书还有没有看三种说法都正确;
(3-2)÷3=,即已看的页数比未看的页数少,因此,已看的页数比未看的页数少说法不正确;
故选:B。
【点睛】本题考查比的意义,解答本题的关键是掌握比的概念。
9.14
【分析】根据“每做对一道得10分,答错扣5分,”可知:答错一题比答对一题少得10+5=15分;假设芳芳小组全部答对得分是10×18=180(分),比120分多得180-120=60(分),那么他们答错了:60÷(10+5)=4(道);所以芳芳小组答对:18-4=14道题。
【详解】[10×(20-2)-120]÷(10+5)
=[10×18-120]÷15
=[180-120]÷15
=60÷15
=4(道)
20-2-4
=18-4
=14(道)
【点睛】鸡兔同笼问题一般利用解设法解答,本题先假设全部答对,得出与实际得分的差就是每道错题对应的失分,从而求出错题数。
10.①②④
【分析】根据题意,结合解答鸡兔同笼问题的方法逐项判断即可。鸡有两只脚,兔子有四只脚,假设笼中全都是鸡或者兔,根据头数(即动物的个数)求出假设时的腿数,再把假设时的腿数与实际情况相比较即可。
【详解】①因为有35个头,则鸡兔一共有35只;说法正确。
②假如全是鸡,共有35×2=70(只)脚,就会少94-70=24(只)脚;说法正确。
③假如全是兔,共有35×4=140(只)脚,就会多140-94=46(只)脚;说法错误。
④如果它们都抬起2只脚,剩下站在地上的脚有:94-35×2=24(只),即24只脚就都是兔子的;说法正确。
综上所述,说法正确的有①②④。
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
11.20
【分析】先把11.5元换成以角为单位的数,即11.5元=115角,假设全是1角钱,由于硬币一共有35枚,则相当于35枚1角的,即35×1=35(角),由于实际有115角,还差了115-35=80(角),这个时候把1角的换成5角的,把一枚1角的换成5角的相当于比原来增加了5-1=4(角),总共差了80角,即80÷4=20(枚),需要把20枚1角钱换成5角的即可。
【详解】假设35枚硬币全是1角的。
11.5元=115角
1×35=35(角)
115-35=80(角)
80÷(5-1)
=80÷4
=20(枚)
【点睛】本题主要考查鸡兔同笼,鸡兔同笼可以利用假设法,或者方程的方法解决。熟练掌握假设法解决应用题并灵活运用。
12. 3∶2 1800
【分析】将这批大米看成单位“1”,用去,还剩下1-=;求剩下的与用去的比,用剩下的分率∶用去的分率即可;用去的比剩下的少-=,是600千克,根据分数除法的意义,用600÷求出大米的质量。再根据分数乘法的意义,用600÷×求出剩下的质量。
【详解】(1-)∶=3∶2
600÷(1--)×
=600÷×
=3000×
=1800(千克)
【点睛】本题主要考查比的意义及“已知一个数的几分之几是多少,求这个数”的实际应用。
13.98
【分析】用故事书比科技书多的本数除以多的份数求出每份是多少,然后用每份数乘故事书的份数即可求出故事书的本数。
【详解】56÷(7-3)×7
=56÷4×7
=14×7
=98(本)
【点睛】此题考查比的应用,熟练掌握总数量÷对应份数=1份量是解题的关键。
14.80
【分析】二班女生与三班男生一样多,这两个班的人数放在一起,男生和女生就各是50人,只要求出一班的女生人数,问题就解决了。一班女生占一班总人数的,据此可以求一班的女生人数;据此解答。
【详解】50+50×
=50+30
=80(人)
【点睛】解决这道题的关键是根据二班女生与三班男生一样多,利用转化的思想,来找出二班和三班的女生人数和相当于一个班的人数。
15. 220 80
【分析】由题意可知:裤子的价钱是上衣的1-=,一套衣服的价钱是上衣的1+,是300元。据此求出上衣的价钱,再用上衣的价钱×即是裤子的价钱。
【详解】300÷(1-+1)
=300÷
=220(元)
220×(1-)
=220×
=80(元)
答:上衣220元,裤子80元。
故答案为:220;80
【点睛】本题主要考查分数四则复合应用题,解题的关键是找出与已知数量对应的分率。
16. 275 85
【分析】假设360个全是猎手,则腿一共有:360×2=720(条),比实际少:890-720=170(条),因为一个猎手比一条狗少2条腿,所以少的是狗的腿的数量,所以狗有:170÷2=85(条),则人有:360-85=275(人),据此解答即可。
【详解】解:假设360个全是猎手,则狗有:
(890-360×2)÷2
=170÷2
=85(条)
猎手有:360-85=275(人)
有275个猎手,85条狗。
【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
17.×
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,反过来不一定成立,举例说明即可。
【详解】圆柱体积30立方米,圆锥体积10立方米,30=15×2=6×5,圆柱底面积可以是15平方米,高是2米,圆锥底面积可以是6平方米,高是5米,不一定等底等高,所以原题说法错误。
故答案为:×
【点睛】关键是理解等底等高的圆柱和圆锥体积之间的关系。
18.×
【分析】盐水是由盐和水组成,题中盐为1份,水是20份,则盐水为21份,所以盐占盐水的,据此进行判断。
【详解】
5%=
故答案为:×
【点睛】理解盐水是由盐和水组成的是解答本题的关键。
19.√
【分析】长方形的周长=(长+宽)×2,长方形的面积=长×宽,周长相等的长方形面积不一定相等;正方形的边长=正方形的周长÷4,因为正方形的周长相等,所以边长也相等,根据正方形的面积计算公式可知,边长相等的正方形,面积一定相等,据此解题。
【详解】周长相等的长方形面积不一定相等,周长相等的正方形面积一定相等。
所以原题说法正确。
【点睛】此题主要考查了学生对长方形和正方形周长面积之间的关系,需要牢记长方形和正方形的面积和周长公式。
20.×
【分析】根据题意可知,前者单位“1”是甲,后者单位“1”是乙,求甲比乙多几分之几,就是(甲-乙)÷乙,而反过来求乙比甲少几分之几,就是(甲-乙)÷甲,由此可以解答。
【详解】红花的朵数比蓝花多几分之几,列式为(红花-蓝花)÷蓝花,而蓝花的朵数比红花少几分之几,列式为(红花-蓝花)÷红花,可以看出除数不一样,得数也不一样。
所以原题说法错误。
【点睛】此题主要考查学生对分数除法的理解,比后面是几就除以几。
21.x+3x=9.6
【分析】观察线段图可知,圆珠笔的价格为x元,钢笔价格是圆珠笔的3倍,即为3x元,钢笔和圆珠笔的总价格为9.6元,据此列方程求解即可。
【详解】解:设圆珠笔的价格为x元,则钢笔的价格是3x元。
x+3x=9.6
4x=9.6
4x÷4=9.6÷4
x=2.4
圆珠笔的单价为2.4元。
【点睛】找出圆珠笔价格x元,钢笔价格3x元,与总价格9.6之间的数量关系是解答此题的关键。
22.篮球有25个
【分析】由图意知:以篮球数量为单位“1”,设篮球有x个,足球的数量相当于篮球的,即,两种球的数量和是40个,即,解此方程即可。
【详解】解:设篮球有x个,足球的有x个。
23.图见详解;20人
【分析】将总人数单位单位“1”,平均分成9份,则男生占4份,女生占9-4=5份。已知女生人数为25人,用女生人数÷求出总人数,总人数×即可求出男生人数;据此解答。
【详解】画图如下:
25÷(1-)×
=25÷×
=25××
=45×
=20(人)
答:男生有20人。
【点睛】本题考查已知一个数的几分之几是多少求这个数及求一个数的几分之几是多少的综合运用。
24.大船5只;小船7只
【分析】设大船x只,则小船有(12-x)只,根据大船数量×每船坐的人数+小船数量×每船坐的人数=总人数,列出方程求出x的值是大船数量,总数量-大船数量=小船数量,据此列式解答。
【详解】解:设大船x只。
5x+(12-x)×3=46
5x+36-3x=46
2x+36-36=46-36
2x÷2=10÷2
x=5
12-5=7(只)
答:大船有5只,小船有7只。
【点睛】用方程解决问题的关键是找到等量关系。
25.450页
【分析】把这本书的页数看作单位“1”,已经看的页数为4份,还剩的页数为5份。已经看的占总页数的。求出25页所占的分率,再用分数除法解题即可。
【详解】
=
=25×18
=450(页)
答:这本书有450页。
【点睛】本题主要考查分数除法的意义。求出25页所占的分率是解题的关键。
26.黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米
【分析】用3680减去辣椒地的面积就是黄瓜、茄子和西红柿的面积和,用黄瓜、茄子和西红柿的面积和减去黄瓜地的面积比西红柿多的120平方米,再加上茄子地的面积比西红柿少的150平方米,就相当于3块西红柿地的面积,再除以3就是1块西红柿地的面积,进一步求出黄瓜地和茄子地的面积。
【详解】3680﹣800=2880(平方米)
(2880﹣120+150)÷3
=2910÷3
=970(平方米)
970+120=1090(平方米)
970﹣150=820(平方米)
答:黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米。
【点睛】解决此题的关键是求出西红柿地的面积。
27.2.8米
【分析】要求木头的长度,先要求出绳子的长度,根据题意,绳子的长度-1.6米=木头的长度,而木头的长度又等于绳子的长度÷2+0.6,所以绳子的长度-1.6米=绳子的长度÷2+0.6,然后列方程解答即可。
【详解】解:设绳子的长度是x米。
x-1.6=x÷2+0.6
x=0.6+1.6
x=2.2÷
x=4.4
4.4-1.6=2.8(米)
答:这根木头长2.8米。
【点睛】本题主要考查列方程解含有两个未知数的问题,解题的关键是找出等量关系式并列出方程。
28.6天
【分析】甲独做10天完成,则甲每天完成这项工作的1÷10=;乙独做5天只能完成全部任务的,则乙每天完成这项工作的÷5=;甲、乙合作一天完成这项工作的+=,两人合作完成全部工作需要1÷=6天;据此解答。
【详解】1÷(1÷10+÷5)
=1÷(+)
=1÷
=6(天)
答:现在两人合作6天才能完成全部工作。
【点睛】本题考查简单的工程问题,解题的关键是求出甲乙工作效率之和。
29.5天
【分析】假设每头牛每天吃青草1份,先求出青草的增加的速度:(22×10-16×10)÷(22-10)=5(份);然后求出草场原有的草的份数:22×10-5×22=110(份);那么27头牛每天吃青草27份,青草每天增加5份,可以看作每天有22头牛在吃草,草场原有的110份的草,可吃,110÷22=5(天)。
【详解】假设每头牛每天吃青草1份,
青草增加的速度:
(22×10-16×10)÷(22-10)
=60÷12
=5(份);
原有的草的份数:
22×10-5×22
=220-110
=110(份);
可供27头牛吃:
110÷(27-5)
=110÷22
=5(天);
答:这个草场的草可供27头牛吃5天。
【点睛】本题考查了牛吃草的问题,关键的是求出青草的每天增加的速度(份数)和草场原有的草的份数。
30.4300元
【解析】设甲的存款为未知数,然后表示出乙的存款,根据甲、乙两人的存款和表示出丙的存款,再根据甲和丙的关系表示出丙的存款,据此列方程求解。
【详解】解:设甲存款为x元;
乙的存款:
丙的存款:
丙的存款:
(元)
答:甲、乙、丙共有存款4300元。
中小学教育资源及组卷应用平台
【点睛】列方程求解应用题的时候,关键是合理设未知数,并准确找出等量关系,然后列方程求解。
