【模块五 四边形】专题3 正方形(含解析)-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块五 四边形】专题3 正方形(含解析)-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 09:34:17 | ||
图片预览


文档简介
2023年中考数学第一轮复习
模块五 四边形
专题3 正方形
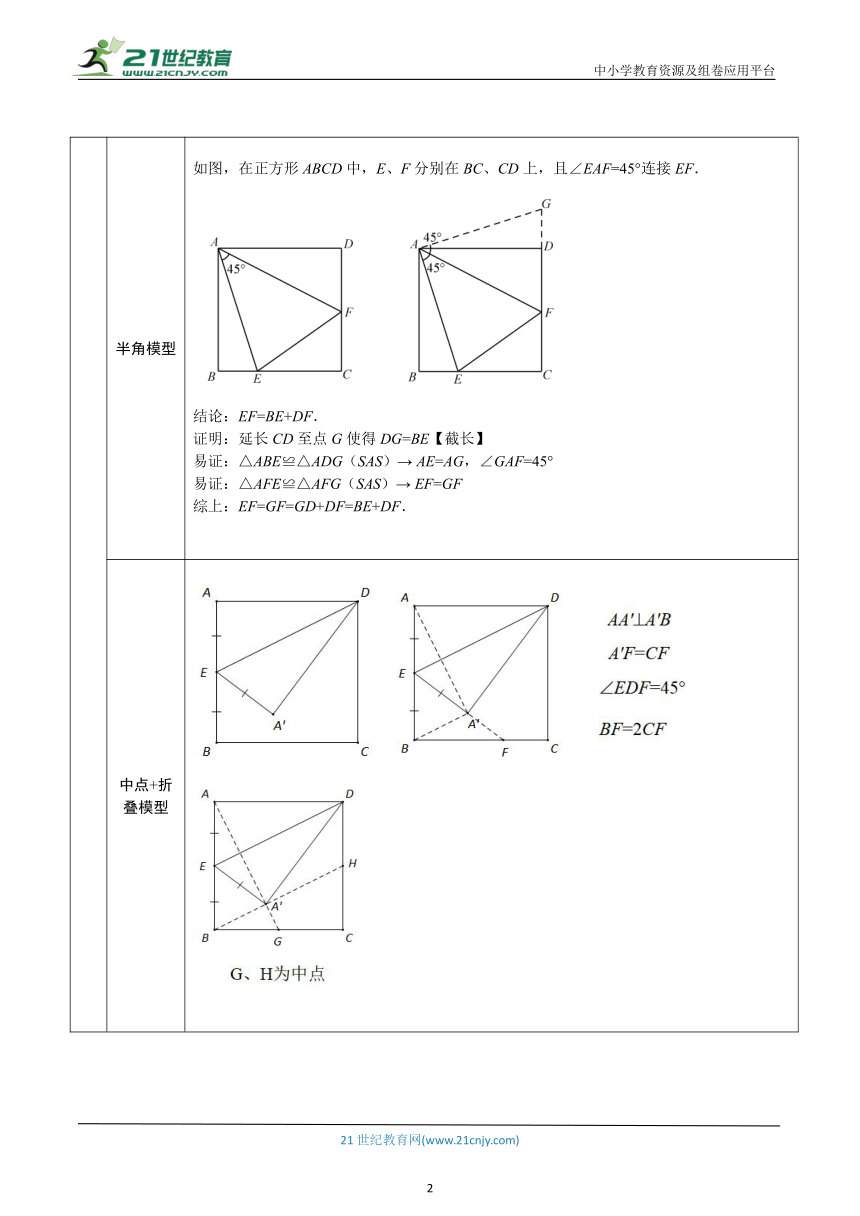
正方形 定义 有一组邻边相等,并且有一个角是直角的平行四边形.
性质 (1)正方形既有矩形的性质,又有菱形的性质. (2)正方形的四个角都是直角,四条边相等. (3)正方形的对角线相等且互相垂直平分.
判定 (1)有一组邻边相等的矩形是正方形. (2)对角线互相垂直的矩形是正方形. (3)有一个角是直角的菱形是正方形. (4)对角线相等的菱形是正方形.
正方形的模型 十字架模型 条件:正方形ABCD,AM⊥BN 条件:正方形ABCD,EF⊥HQ 结论:AM=BN 结论:EF=FQ
对角线模型
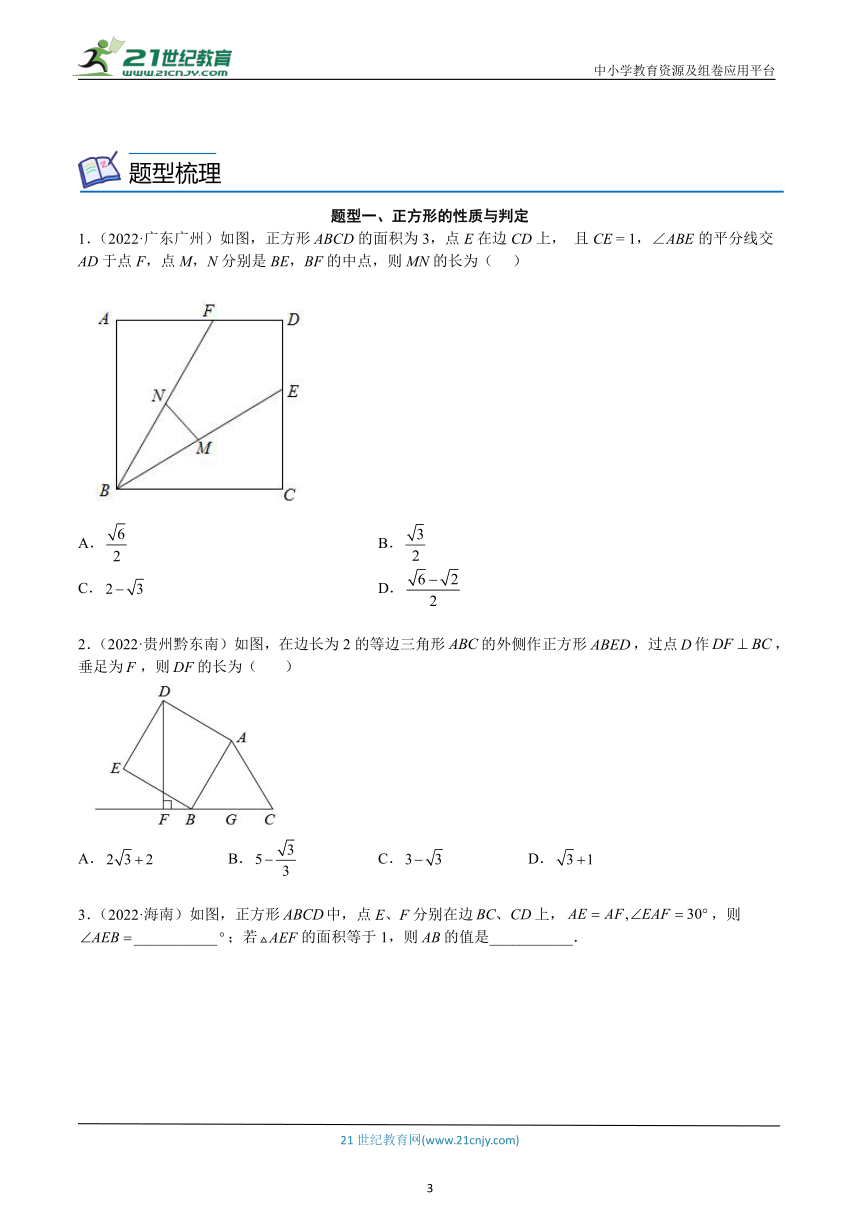
半角模型 如图,在正方形ABCD中,E、F分别在BC、CD上,且∠EAF=45°连接EF. 结论:EF=BE+DF. 证明:延长CD至点G使得DG=BE【截长】 易证:△ABE≌△ADG(SAS)→ AE=AG,∠GAF=45° 易证:△AFE≌△AFG(SAS)→ EF=GF 综上:EF=GF=GD+DF=BE+DF.
中点+折叠模型
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、正方形的性质与判定
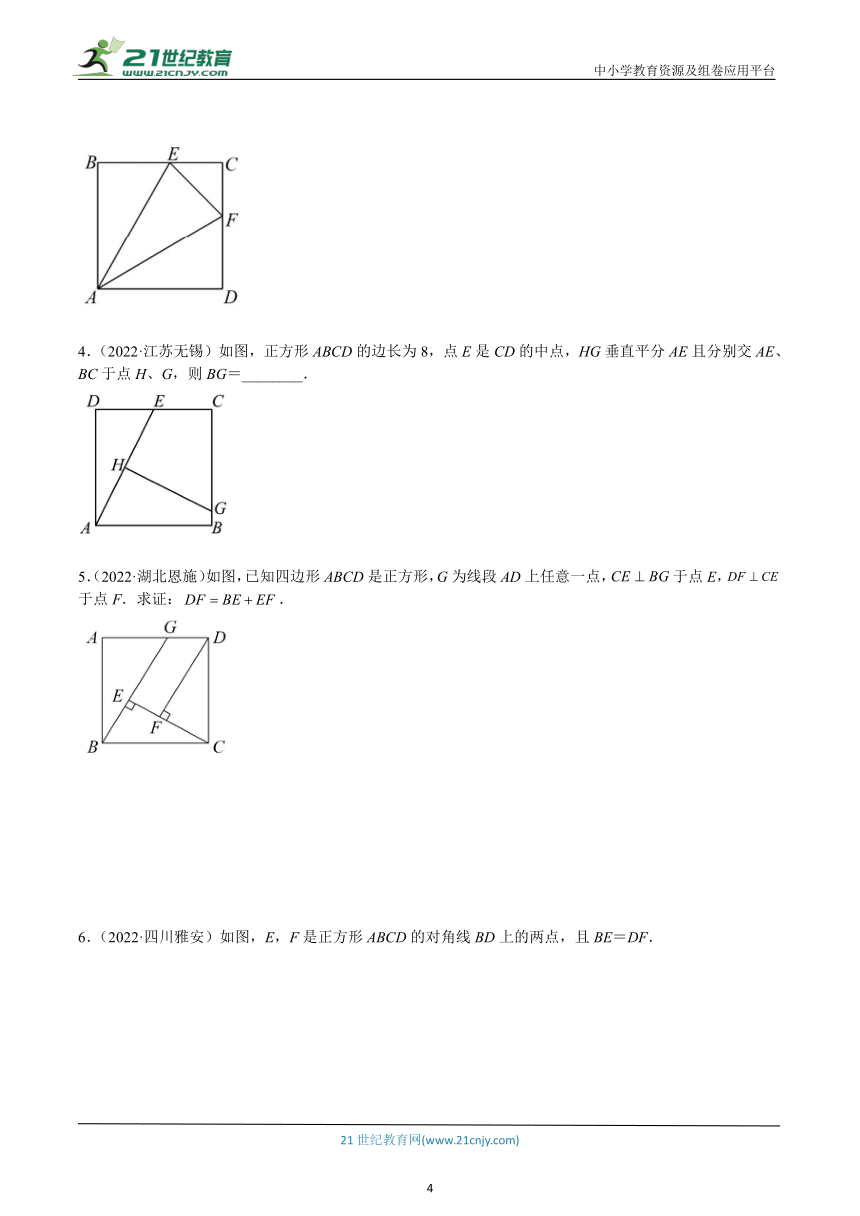
1.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
2.(2022·贵州黔东南)如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
3.(2022·海南)如图,正方形中,点E、F分别在边上,,则___________;若的面积等于1,则的值是___________.
4.(2022·江苏无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=________.
5.(2022·湖北恩施)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
6.(2022·四川雅安)如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)若AB=3,BE=2,求四边形AECF的面积.
题型二、正方形的常考模型
1.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
2.(2022·黑龙江)如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若,则;⑤四边形OECF的面积是正方形ABCD面积的.其中正确的结论是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
3.(2021·山东东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若,则GE的长为________.
4.(2022·黑龙江大庆)如图,正方形中,点E,F分别是边上的两个动点,且正方形的周长是周长的2倍,连接分别与对角线交于点M,N.给出如下几个结论:①若,则;②;③若,则;④若,则.其中正确结论的序号为____________.
5.(2022·贵州贵阳)如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
6.(2021·山东德州)如图,点,分别在正方形的边,上,且,点,分别在边,上,且,垂足为
(1)求证:FG=EH;
(2)若正方形边长为5,,,求的长度.
7.(2022·河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
8.(2022·内蒙古赤峰)同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】如图①,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
题型三、正方形的动态问题
1.(2022·内蒙古通辽)已知点在正方形的对角线上,正方形与正方形有公共点.
(1)如图1,当点在上,在上,求的值为多少;
(2)将正方形绕点逆时针方向旋转,如图2,求:的值为多少;
(3),,将正方形绕逆时针方向旋转,当,,三点共线时,请直接写出的长度.
2023年中考数学第一轮复习
模块五 四边形
专题3 正方形
正方形 定义 有一组邻边相等,并且有一个角是直角的平行四边形.
性质 (1)正方形既有矩形的性质,又有菱形的性质. (2)正方形的四个角都是直角,四条边相等. (3)正方形的对角线相等且互相垂直平分.
判定 (1)有一组邻边相等的矩形是正方形. (2)对角线互相垂直的矩形是正方形. (3)有一个角是直角的菱形是正方形. (4)对角线相等的菱形是正方形.
正方形的模型 十字架模型 条件:正方形ABCD,AM⊥BN 条件:正方形ABCD,EF⊥HQ 结论:AM=BN 结论:EF=FQ
对角线模型
半角模型 如图,在正方形ABCD中,E、F分别在BC、CD上,且∠EAF=45°连接EF. 结论:EF=BE+DF. 证明:延长CD至点G使得DG=BE【截长】 易证:△ABE≌△ADG(SAS)→ AE=AG,∠GAF=45° 易证:△AFE≌△AFG(SAS)→ EF=GF 综上:EF=GF=GD+DF=BE+DF.
中点+折叠模型
题型一、正方形的性质与判定
1.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
如图,连接EF,先证明 再求解 可得 再求解 可得为等腰直角三角形,求解 再利用三角形的中位线的性质可得答案.
【详解】
解:如图,连接EF,
∵正方形ABCD的面积为3,
∵
∴
∴
∴
∵平分
∴
∴
∴为等腰直角三角形,
∵分别为的中点,
故选D
2.(2022·贵州黔东南)如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
【答案】D
【分析】过点A分别作AG⊥BC于点G,AH⊥DF于点H,可得四边形AGFH是矩形,从而得到FH=AG,再由△ABC为等边三角形,可得∠BAG=30°,BG=1,从而得到,再证得∠DAH=∠BAG=30°,然后根据直角三角形的性质,即可求解.
【详解】解:如图,过点A分别作AG⊥BC于点G,AH⊥DF于点H,
∵DF⊥BC,∴∠GFH=∠AHF=∠AGF=90°,
∴四边形AGFH是矩形,∴FH=AG,
∵△ABC为等边三角形,∴∠BAC=60°,BC=AB=2,
∴∠BAG=30°,BG=1,∴,∴,
在正方形ABED中,AD=AB=2,∠BAD=90°,∴∠DAH=∠BAG=30°,
∴,∴.故选:D
【点睛】本题主要考查了等边三角形和正方形的性质,直角三角形的性质,熟练掌握等边三角形和正方形的性质,直角三角形的性质是解题的关键.
3.(2022·海南)如图,正方形中,点E、F分别在边上,,则___________;若的面积等于1,则的值是___________.
【答案】 60
【分析】由正方形的性质证明,即可得到,再由可得,即可求出.设,表示出的面积,解方程即可.
【详解】∵正方形
∴,
∵
∴(HL)
∴,
∵,
∴
∴
设
∴
∴
∵的面积等于1
∴,解得,(舍去)
∴
故答案为:60;.
【点睛】本题考查正方形的性质、全等三角形的判定与性质、30°直角三角形的性质,熟练掌握正方形的性质,证明三角形全等是解题的关键.
4.(2022·江苏无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=________.
【答案】1
【分析】连接AG,EG,根据线段垂直平分线性质可得AG=EG,由点E是CD的中点,得CE=4,设BG=x,则CG=8-x,由勾股定理,可得出(8-x)2+42=82+x2,求解即可.
【详解】解:连接AG,EG,如图,
∵HG垂直平分AE,
∴AG=EG,
∵正方形ABCD的边长为8,
∴∠B=∠C=90°,AB=BC=CD=8,
∵点E是CD的中点,
∴CE=4,
设BG=x,则CG=8-x,
由勾股定理,得
EG2=CG2+CE2=(8-x)2+42,AG2=AB2+BG2=82+x2,
∴(8-x)2+42=82+x2,
解得:x=1,
故答案为:1.
【点睛】本题考查正方形的性质,线段垂直平分线的性质,勾股定理,熟练掌握正方形的性质、线段垂直平分线的性质、勾股定理及其运用是解题的关键.
5.(2022·湖北恩施)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
【答案】证明见解析
【解析】
【分析】
先根据正方形的性质可得,从而可得,再根据垂直的定义可得,从而可得,然后根据三角形全等的判定定理证出,根据全等三角形的性质可得,最后根据线段的和差、等量代换即可得证.
【详解】
证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
【点睛】
本题考查了正方形的性质、三角形全等的判定与性质等知识点,正确找出两个全等三角形是解题关键.
6.(2022·四川雅安)如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)若AB=3,BE=2,求四边形AECF的面积.
【答案】(1)证明见解析
(2)6
【分析】(1)利用正方形的性质证明再结合BE=DF,从而可得结论;
(2)先利用正方形的性质证明 再求解EF的长,再利用四边形AECF的面积,即可得到答案.
(1)
证明: 正方形ABCD,
(2)
如图,连结AC,
正方形ABCD,
∴四边形AECF的面积
【点睛】本题考查的是全等三角形的判定与性质,正方形的性质,勾股定理的应用,二次根式的乘法运算,掌握“正方形的对角线相等且互相垂直平分”是解本题的关键.
题型二、正方形的常考模型
1.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
【答案】C
【解析】
【分析】
由正方形的性质得出,,由证得,即可得出答案.
【详解】
解:四边形是正方形,
,,
∵在中,,
,
设,则,
根据勾股定理得:,
即,
解得:(负值舍去),
,
,
,
,
,
,,
,
.
故选:.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,含角的直角三角形的性质等知识,证明是解题的关键.
2.(2022·黑龙江)如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若,则;⑤四边形OECF的面积是正方形ABCD面积的.其中正确的结论是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
【答案】B
【分析】分别对每个选项进行证明后进行判断:
①通过证明得到EC=FD,再证明得到∠EAC=∠FBD,从而证明∠BPQ=∠AOQ=90°,即;
②通过等弦对等角可证明;
③通过正切定义得,利用合比性质变形得到,再通过证明得到,代入前式得,最后根据三角形面积公式得到,整体代入即可证得结论正确;
④作EG⊥AC于点G可得EGBO,根据,设正方形边长为5a,分别求出EG、AC、CG的长,可求出,结论错误;
⑤将四边形OECF的面积分割成两个三角形面积,利用,可证明S四边形OECF=S△COE+S△COF= S△DOF+S△COF =S△COD即可证明结论正确.
【详解】①∵四边形ABCD是正方形,O是对角线AC、BD的交点,
∴OC=OD,OC⊥OD,∠ODF=∠OCE=45°
∵∴∠DOF+∠FOC=∠FOC+∠EOC=90°∴∠DOF=∠EOC
在△DOF与△COE中∴∴EC=FD
∵在△EAC与△FBD中∴∴∠EAC=∠FBD
又∵∠BQP=∠AQO∴∠BPQ=∠AOQ=90°∴AE⊥BF所以①正确;
②∵∠AOB=∠APB=90°∴点P、O在以AB为直径的圆上
∴AO是该圆的弦∴所以②正确;
③∵∴∴
∴∴
∵∴∴
∴∴
∵∴
∴所以③正确;
④作EG⊥AC于点G,则EGBO,∴
设正方形边长为5a,则BC=5a,OB=OC=,
若,则,∴∴
∴
∵EG⊥AC,∠ACB=45°,∴∠GEC=45°∴CG=EG=
∴所以④错误;
⑤∵,S四边形OECF=S△COE+S△COF
∴S四边形OECF= S△DOF+S△COF= S△COD
∵S△COD=∴S四边形OECF=所以⑤正确;
综上,①②③⑤正确,④错误,故选 B
【点睛】本题综合考查了三角形、正方形、圆和三角函数,熟练运用全等三角形、相似三角形、等弦对等角和三角函数的定义是解题的关键.
3.(2021·山东东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若,则GE的长为________.
【答案】
【解析】
【分析】
因为折叠,则有,从而可知,利用线段比求出DG的长,即可求出EG.
【详解】
如图, 四边形ABCD是正方形,
,
因为折叠,,设垂足为H,
,
,
,
,
,
,,DE=,
,
,
故答案为.
【点睛】
本题考查了正方形的性质,轴对称的性质,三角形相似的判定与性质,勾股定理,找到是解题的关键.
4.(2022·黑龙江大庆)如图,正方形中,点E,F分别是边上的两个动点,且正方形的周长是周长的2倍,连接分别与对角线交于点M,N.给出如下几个结论:①若,则;②;③若,则;④若,则.其中正确结论的序号为____________.
【答案】②
【分析】根据已知条件可得,即可判断①,进而推出,导角可得②正确,作于点,连接,证明是直角三角形,勾股定理验证③,证明,即可判断④求解.
【详解】解:∵正方形的周长是周长的2倍,
∴,
,
①若,则,故①不正确;
如图,在的延长线上取点,使得,
四边形是正方形,
,,
,
,,,
,,
,
,,,
,
,
,
,
即,故②正确;
如图,作于点,连接,
则,
,,
,
同理可得,
,
关于对称轴,关于对称,
,
,
,
是直角三角形,
③若,
,
,故③不正确,
,
若,
即,
,
,,
又,
,
,
即,
,
,
,
,
,
故④不正确.
故答案为:②.
【点睛】本题考查了正方形的性质,轴对称的性质,解直角三角形,全等三角形的性质与判定,掌握以上知识是解题的关键.
5.(2022·贵州贵阳)如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
【答案】(1)见详解
(2)
【分析】(1)先证明四边形ADFM是矩形,得到AD=MF,∠AMF=90°=∠MFD,再利用MN⊥BE证得∠MBO=∠OMF,结合∠A=90°=∠NFM即可证明;
(2)利用勾股定理求得BE=10=MN,根据垂直平分线的性质可得BO=OE=5,BM=ME,即有AM=AB-BM=8-ME,在Rt△AME中,,可得,解得:,即有,再在Rt△BMO中利用勾股定理即可求出MO,则NO可求.
(1)
在正方形ABCD中,有AD=DC=CB=AB,∠A=∠D=∠C=90°,,
,
∵,∠A=∠D=90°,,
∴四边形ADFM是矩形,
∴AD=MF,∠AMF=90°=∠MFD,
∴∠BMF=90°=∠NFM,即∠BMO+∠OMF=90°,AB=AD=MF,
∵MN是BE的垂直平分线,
∴MN⊥BE,
∴∠BOM=90°=∠BMO+∠MBO,
∴∠MBO=∠OMF,
∵,
∴△ABE≌△FMN;
(2)
连接ME,如图,
∵AB=8,AE=6,
∴在Rt△ABE中,,
∴根据(1)中全等的结论可知MN=BE=10,
∵MN是BE的垂直平分线,
∴BO=OE==5,BM=ME,
∴AM=AB-BM=8-ME,
∴在Rt△AME中,,
∴,解得:,
∴,
∴在Rt△BMO中,,
∴,
∴ON=MN-MO=.
即NO的长为:.
【点睛】本题考查了矩形的判定与性质、正方形的性质、垂直平分线的性质、勾股定理、全等三角形的判定与性质等知识,掌握勾股定理是解答本题的关键.
6.(2021·山东德州)如图,点,分别在正方形的边,上,且,点,分别在边,上,且,垂足为.
(1)求证:;
(2)若正方形边长为5,,,求的长度.
【答案】(1)答案见解析;
(2)
【解析】
【分析】
(1)根据正方形的性质得出AD= AB,∠A=∠B= 90°,得到AF= BE,再根据垂直的定义进而得出∠AFG =∠BEH,即可根据ASA证明△AFG≌△BEH,根据全等三角形的性质即可得解;
(2)先求出AG的长,在根据勾股定理求出FG的长,再证△AFG∽△PEG,由性质求出PG的长,最后根据PF=FG-PG,可得答案.
(1)
解:∵四边形ABCD是正方形,
∴AD= AB,∠A=∠B= 90°,
∴∠AGF+∠AFG = 90°,
∵FG⊥ EH,
∴∠AGF+∠GEP= 90°,
∴∠AFG=∠GEP=∠BEH
∵AE= DF,
∴AD- DF= AB- AE,
即AF= BE,
在△AFG和△BEH中,
,
∴△AFG≌△BEH
∴FG=EH;
(2)
∵AB=AD=5,DF=AE=2,
∴BE=AF=5-2=3,
在RT△AFG中,,
∴AG=4,
∴EG=2,
在RT△AFG中,,
∵∠A=∠FPG=90°,∠AGF=∠PGE,
∴△AFG∽△PEG,
∴ ,
即,
∴PG= ,
∴PF=FG-PG=5-=.
【点睛】
本题考查了正方形的性质、全等三角形的判定与性质、勾股定理的应用、相似三角形的判定与性质等知识,解题的关键是熟记相似三角形的判定与性质.
7.(2022·河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
【答案】(1)或或或
(2)①15,15;②,理由见解析
(3)cm或
【解析】
【分析】
(1)根据折叠的性质,得,结合矩形的性质得,进而可得;
(2)根据折叠的性质,可证,即可求解;
(3)由(2)可得,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设分别表示出PD,DQ,PQ,由勾股定理即可求解.
(1)
解:
(2)
∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
②
(3)
当点Q在点F的下方时,如图,
,DQ=DF+FQ=4+1=5(cm)
由(2)可知,
设
,
即
解得:
∴;
当当点Q在点F的上方时,如图,
cm,DQ =3cm,
由(2)可知,
设
,
即
解得:
∴.
【点睛】
本题主要考查矩形与折叠,正方形的性质、勾股定理、三角形的全等,掌握相关知识并灵活应用是解题的关键.
8.(2022·内蒙古赤峰)同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】如图①,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
【答案】(1)
(2)16
(3)或
【分析】(1)由正方形的性质可得,,根据ASA可证,由全等三角形的性质可得结论;
(2) 过点O作交AD于点M,交BC于点N,作交AB于点T,交CD于点R,证明△进而证明;
(3)分别求出,由勾股定理可得方程,求出x的值即可.
(1)
∵四边形ABCD是正方形,
∴∠
∵是对角线,
∴∠,
∴∠,
∵四边形是正方形,
∴∠,
∴∠
又∠
∴,
∴
∴
故答案为:
(2)
过点O作交AD于点M,交BC于点N,作交AB于点T,交CD于点R,如图,
∵点O是正方形ABCD的中心,
∴
又∠A=90°
∴四边形ATOM是正方形,
∴
同(1)可证△
∴
(3)
∵四边形均为正方形,
∴∠
∵CG在CD上,
∴
又CE在BC的延长线上,
∴
设则
在中,
在中,
延长AD,CE交于点Q,则四边形是矩形,
∴
∴,
在中,
若△为直角三角形,则有,
即
整理得,
解得,
∴或
【点睛】本题主要考查了正方形的性质,全等三角形的判定与性质,矩形的判定,勾股定理等知识,正确作出辅助线是解答本题的关键
题型三、正方形的动态问题
1.(2022·内蒙古通辽)已知点在正方形的对角线上,正方形与正方形有公共点.
(1)如图1,当点在上,在上,求的值为多少;
(2)将正方形绕点逆时针方向旋转,如图2,求:的值为多少;
(3),,将正方形绕逆时针方向旋转,当,,三点共线时,请直接写出的长度.
【答案】(1)2
(2)
(3)
【分析】(1)根据题意可得,根据平行线分线段成比例即可求解;
(2)根据(1)的结论,可得,根据旋转的性质可得,进而证明,根据相似三角形的性质即可求解;
(3)勾股定理求得,,进而根据,由相似三角形的性质即可求解.
(1)
正方形与正方形有公共点,点在上,在上,
四边形是正方形
(2)
如图,连接,
正方形绕点逆时针方向旋转,
,
(3)
如图,
,,
,,,
三点共线,
中,,
,
由(2)可知,
,
.
【点睛】本题考查了平行线分线段成比例,相似三角形的性质与判定,正方形的性质,勾股定理,旋转的性质,综合运用以上知识是解题的关键.
模块五 四边形
专题3 正方形
正方形 定义 有一组邻边相等,并且有一个角是直角的平行四边形.
性质 (1)正方形既有矩形的性质,又有菱形的性质. (2)正方形的四个角都是直角,四条边相等. (3)正方形的对角线相等且互相垂直平分.
判定 (1)有一组邻边相等的矩形是正方形. (2)对角线互相垂直的矩形是正方形. (3)有一个角是直角的菱形是正方形. (4)对角线相等的菱形是正方形.
正方形的模型 十字架模型 条件:正方形ABCD,AM⊥BN 条件:正方形ABCD,EF⊥HQ 结论:AM=BN 结论:EF=FQ
对角线模型
半角模型 如图,在正方形ABCD中,E、F分别在BC、CD上,且∠EAF=45°连接EF. 结论:EF=BE+DF. 证明:延长CD至点G使得DG=BE【截长】 易证:△ABE≌△ADG(SAS)→ AE=AG,∠GAF=45° 易证:△AFE≌△AFG(SAS)→ EF=GF 综上:EF=GF=GD+DF=BE+DF.
中点+折叠模型
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、正方形的性质与判定
1.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
2.(2022·贵州黔东南)如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
3.(2022·海南)如图,正方形中,点E、F分别在边上,,则___________;若的面积等于1,则的值是___________.
4.(2022·江苏无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=________.
5.(2022·湖北恩施)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
6.(2022·四川雅安)如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)若AB=3,BE=2,求四边形AECF的面积.
题型二、正方形的常考模型
1.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
2.(2022·黑龙江)如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若,则;⑤四边形OECF的面积是正方形ABCD面积的.其中正确的结论是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
3.(2021·山东东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若,则GE的长为________.
4.(2022·黑龙江大庆)如图,正方形中,点E,F分别是边上的两个动点,且正方形的周长是周长的2倍,连接分别与对角线交于点M,N.给出如下几个结论:①若,则;②;③若,则;④若,则.其中正确结论的序号为____________.
5.(2022·贵州贵阳)如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
6.(2021·山东德州)如图,点,分别在正方形的边,上,且,点,分别在边,上,且,垂足为
(1)求证:FG=EH;
(2)若正方形边长为5,,,求的长度.
7.(2022·河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
8.(2022·内蒙古赤峰)同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】如图①,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
题型三、正方形的动态问题
1.(2022·内蒙古通辽)已知点在正方形的对角线上,正方形与正方形有公共点.
(1)如图1,当点在上,在上,求的值为多少;
(2)将正方形绕点逆时针方向旋转,如图2,求:的值为多少;
(3),,将正方形绕逆时针方向旋转,当,,三点共线时,请直接写出的长度.
2023年中考数学第一轮复习
模块五 四边形
专题3 正方形
正方形 定义 有一组邻边相等,并且有一个角是直角的平行四边形.
性质 (1)正方形既有矩形的性质,又有菱形的性质. (2)正方形的四个角都是直角,四条边相等. (3)正方形的对角线相等且互相垂直平分.
判定 (1)有一组邻边相等的矩形是正方形. (2)对角线互相垂直的矩形是正方形. (3)有一个角是直角的菱形是正方形. (4)对角线相等的菱形是正方形.
正方形的模型 十字架模型 条件:正方形ABCD,AM⊥BN 条件:正方形ABCD,EF⊥HQ 结论:AM=BN 结论:EF=FQ
对角线模型
半角模型 如图,在正方形ABCD中,E、F分别在BC、CD上,且∠EAF=45°连接EF. 结论:EF=BE+DF. 证明:延长CD至点G使得DG=BE【截长】 易证:△ABE≌△ADG(SAS)→ AE=AG,∠GAF=45° 易证:△AFE≌△AFG(SAS)→ EF=GF 综上:EF=GF=GD+DF=BE+DF.
中点+折叠模型
题型一、正方形的性质与判定
1.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
如图,连接EF,先证明 再求解 可得 再求解 可得为等腰直角三角形,求解 再利用三角形的中位线的性质可得答案.
【详解】
解:如图,连接EF,
∵正方形ABCD的面积为3,
∵
∴
∴
∴
∵平分
∴
∴
∴为等腰直角三角形,
∵分别为的中点,
故选D
2.(2022·贵州黔东南)如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
【答案】D
【分析】过点A分别作AG⊥BC于点G,AH⊥DF于点H,可得四边形AGFH是矩形,从而得到FH=AG,再由△ABC为等边三角形,可得∠BAG=30°,BG=1,从而得到,再证得∠DAH=∠BAG=30°,然后根据直角三角形的性质,即可求解.
【详解】解:如图,过点A分别作AG⊥BC于点G,AH⊥DF于点H,
∵DF⊥BC,∴∠GFH=∠AHF=∠AGF=90°,
∴四边形AGFH是矩形,∴FH=AG,
∵△ABC为等边三角形,∴∠BAC=60°,BC=AB=2,
∴∠BAG=30°,BG=1,∴,∴,
在正方形ABED中,AD=AB=2,∠BAD=90°,∴∠DAH=∠BAG=30°,
∴,∴.故选:D
【点睛】本题主要考查了等边三角形和正方形的性质,直角三角形的性质,熟练掌握等边三角形和正方形的性质,直角三角形的性质是解题的关键.
3.(2022·海南)如图,正方形中,点E、F分别在边上,,则___________;若的面积等于1,则的值是___________.
【答案】 60
【分析】由正方形的性质证明,即可得到,再由可得,即可求出.设,表示出的面积,解方程即可.
【详解】∵正方形
∴,
∵
∴(HL)
∴,
∵,
∴
∴
设
∴
∴
∵的面积等于1
∴,解得,(舍去)
∴
故答案为:60;.
【点睛】本题考查正方形的性质、全等三角形的判定与性质、30°直角三角形的性质,熟练掌握正方形的性质,证明三角形全等是解题的关键.
4.(2022·江苏无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=________.
【答案】1
【分析】连接AG,EG,根据线段垂直平分线性质可得AG=EG,由点E是CD的中点,得CE=4,设BG=x,则CG=8-x,由勾股定理,可得出(8-x)2+42=82+x2,求解即可.
【详解】解:连接AG,EG,如图,
∵HG垂直平分AE,
∴AG=EG,
∵正方形ABCD的边长为8,
∴∠B=∠C=90°,AB=BC=CD=8,
∵点E是CD的中点,
∴CE=4,
设BG=x,则CG=8-x,
由勾股定理,得
EG2=CG2+CE2=(8-x)2+42,AG2=AB2+BG2=82+x2,
∴(8-x)2+42=82+x2,
解得:x=1,
故答案为:1.
【点睛】本题考查正方形的性质,线段垂直平分线的性质,勾股定理,熟练掌握正方形的性质、线段垂直平分线的性质、勾股定理及其运用是解题的关键.
5.(2022·湖北恩施)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
【答案】证明见解析
【解析】
【分析】
先根据正方形的性质可得,从而可得,再根据垂直的定义可得,从而可得,然后根据三角形全等的判定定理证出,根据全等三角形的性质可得,最后根据线段的和差、等量代换即可得证.
【详解】
证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
【点睛】
本题考查了正方形的性质、三角形全等的判定与性质等知识点,正确找出两个全等三角形是解题关键.
6.(2022·四川雅安)如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)若AB=3,BE=2,求四边形AECF的面积.
【答案】(1)证明见解析
(2)6
【分析】(1)利用正方形的性质证明再结合BE=DF,从而可得结论;
(2)先利用正方形的性质证明 再求解EF的长,再利用四边形AECF的面积,即可得到答案.
(1)
证明: 正方形ABCD,
(2)
如图,连结AC,
正方形ABCD,
∴四边形AECF的面积
【点睛】本题考查的是全等三角形的判定与性质,正方形的性质,勾股定理的应用,二次根式的乘法运算,掌握“正方形的对角线相等且互相垂直平分”是解本题的关键.
题型二、正方形的常考模型
1.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
【答案】C
【解析】
【分析】
由正方形的性质得出,,由证得,即可得出答案.
【详解】
解:四边形是正方形,
,,
∵在中,,
,
设,则,
根据勾股定理得:,
即,
解得:(负值舍去),
,
,
,
,
,
,,
,
.
故选:.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,含角的直角三角形的性质等知识,证明是解题的关键.
2.(2022·黑龙江)如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若,则;⑤四边形OECF的面积是正方形ABCD面积的.其中正确的结论是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
【答案】B
【分析】分别对每个选项进行证明后进行判断:
①通过证明得到EC=FD,再证明得到∠EAC=∠FBD,从而证明∠BPQ=∠AOQ=90°,即;
②通过等弦对等角可证明;
③通过正切定义得,利用合比性质变形得到,再通过证明得到,代入前式得,最后根据三角形面积公式得到,整体代入即可证得结论正确;
④作EG⊥AC于点G可得EGBO,根据,设正方形边长为5a,分别求出EG、AC、CG的长,可求出,结论错误;
⑤将四边形OECF的面积分割成两个三角形面积,利用,可证明S四边形OECF=S△COE+S△COF= S△DOF+S△COF =S△COD即可证明结论正确.
【详解】①∵四边形ABCD是正方形,O是对角线AC、BD的交点,
∴OC=OD,OC⊥OD,∠ODF=∠OCE=45°
∵∴∠DOF+∠FOC=∠FOC+∠EOC=90°∴∠DOF=∠EOC
在△DOF与△COE中∴∴EC=FD
∵在△EAC与△FBD中∴∴∠EAC=∠FBD
又∵∠BQP=∠AQO∴∠BPQ=∠AOQ=90°∴AE⊥BF所以①正确;
②∵∠AOB=∠APB=90°∴点P、O在以AB为直径的圆上
∴AO是该圆的弦∴所以②正确;
③∵∴∴
∴∴
∵∴∴
∴∴
∵∴
∴所以③正确;
④作EG⊥AC于点G,则EGBO,∴
设正方形边长为5a,则BC=5a,OB=OC=,
若,则,∴∴
∴
∵EG⊥AC,∠ACB=45°,∴∠GEC=45°∴CG=EG=
∴所以④错误;
⑤∵,S四边形OECF=S△COE+S△COF
∴S四边形OECF= S△DOF+S△COF= S△COD
∵S△COD=∴S四边形OECF=所以⑤正确;
综上,①②③⑤正确,④错误,故选 B
【点睛】本题综合考查了三角形、正方形、圆和三角函数,熟练运用全等三角形、相似三角形、等弦对等角和三角函数的定义是解题的关键.
3.(2021·山东东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若,则GE的长为________.
【答案】
【解析】
【分析】
因为折叠,则有,从而可知,利用线段比求出DG的长,即可求出EG.
【详解】
如图, 四边形ABCD是正方形,
,
因为折叠,,设垂足为H,
,
,
,
,
,
,,DE=,
,
,
故答案为.
【点睛】
本题考查了正方形的性质,轴对称的性质,三角形相似的判定与性质,勾股定理,找到是解题的关键.
4.(2022·黑龙江大庆)如图,正方形中,点E,F分别是边上的两个动点,且正方形的周长是周长的2倍,连接分别与对角线交于点M,N.给出如下几个结论:①若,则;②;③若,则;④若,则.其中正确结论的序号为____________.
【答案】②
【分析】根据已知条件可得,即可判断①,进而推出,导角可得②正确,作于点,连接,证明是直角三角形,勾股定理验证③,证明,即可判断④求解.
【详解】解:∵正方形的周长是周长的2倍,
∴,
,
①若,则,故①不正确;
如图,在的延长线上取点,使得,
四边形是正方形,
,,
,
,,,
,,
,
,,,
,
,
,
,
即,故②正确;
如图,作于点,连接,
则,
,,
,
同理可得,
,
关于对称轴,关于对称,
,
,
,
是直角三角形,
③若,
,
,故③不正确,
,
若,
即,
,
,,
又,
,
,
即,
,
,
,
,
,
故④不正确.
故答案为:②.
【点睛】本题考查了正方形的性质,轴对称的性质,解直角三角形,全等三角形的性质与判定,掌握以上知识是解题的关键.
5.(2022·贵州贵阳)如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
【答案】(1)见详解
(2)
【分析】(1)先证明四边形ADFM是矩形,得到AD=MF,∠AMF=90°=∠MFD,再利用MN⊥BE证得∠MBO=∠OMF,结合∠A=90°=∠NFM即可证明;
(2)利用勾股定理求得BE=10=MN,根据垂直平分线的性质可得BO=OE=5,BM=ME,即有AM=AB-BM=8-ME,在Rt△AME中,,可得,解得:,即有,再在Rt△BMO中利用勾股定理即可求出MO,则NO可求.
(1)
在正方形ABCD中,有AD=DC=CB=AB,∠A=∠D=∠C=90°,,
,
∵,∠A=∠D=90°,,
∴四边形ADFM是矩形,
∴AD=MF,∠AMF=90°=∠MFD,
∴∠BMF=90°=∠NFM,即∠BMO+∠OMF=90°,AB=AD=MF,
∵MN是BE的垂直平分线,
∴MN⊥BE,
∴∠BOM=90°=∠BMO+∠MBO,
∴∠MBO=∠OMF,
∵,
∴△ABE≌△FMN;
(2)
连接ME,如图,
∵AB=8,AE=6,
∴在Rt△ABE中,,
∴根据(1)中全等的结论可知MN=BE=10,
∵MN是BE的垂直平分线,
∴BO=OE==5,BM=ME,
∴AM=AB-BM=8-ME,
∴在Rt△AME中,,
∴,解得:,
∴,
∴在Rt△BMO中,,
∴,
∴ON=MN-MO=.
即NO的长为:.
【点睛】本题考查了矩形的判定与性质、正方形的性质、垂直平分线的性质、勾股定理、全等三角形的判定与性质等知识,掌握勾股定理是解答本题的关键.
6.(2021·山东德州)如图,点,分别在正方形的边,上,且,点,分别在边,上,且,垂足为.
(1)求证:;
(2)若正方形边长为5,,,求的长度.
【答案】(1)答案见解析;
(2)
【解析】
【分析】
(1)根据正方形的性质得出AD= AB,∠A=∠B= 90°,得到AF= BE,再根据垂直的定义进而得出∠AFG =∠BEH,即可根据ASA证明△AFG≌△BEH,根据全等三角形的性质即可得解;
(2)先求出AG的长,在根据勾股定理求出FG的长,再证△AFG∽△PEG,由性质求出PG的长,最后根据PF=FG-PG,可得答案.
(1)
解:∵四边形ABCD是正方形,
∴AD= AB,∠A=∠B= 90°,
∴∠AGF+∠AFG = 90°,
∵FG⊥ EH,
∴∠AGF+∠GEP= 90°,
∴∠AFG=∠GEP=∠BEH
∵AE= DF,
∴AD- DF= AB- AE,
即AF= BE,
在△AFG和△BEH中,
,
∴△AFG≌△BEH
∴FG=EH;
(2)
∵AB=AD=5,DF=AE=2,
∴BE=AF=5-2=3,
在RT△AFG中,,
∴AG=4,
∴EG=2,
在RT△AFG中,,
∵∠A=∠FPG=90°,∠AGF=∠PGE,
∴△AFG∽△PEG,
∴ ,
即,
∴PG= ,
∴PF=FG-PG=5-=.
【点睛】
本题考查了正方形的性质、全等三角形的判定与性质、勾股定理的应用、相似三角形的判定与性质等知识,解题的关键是熟记相似三角形的判定与性质.
7.(2022·河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
【答案】(1)或或或
(2)①15,15;②,理由见解析
(3)cm或
【解析】
【分析】
(1)根据折叠的性质,得,结合矩形的性质得,进而可得;
(2)根据折叠的性质,可证,即可求解;
(3)由(2)可得,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设分别表示出PD,DQ,PQ,由勾股定理即可求解.
(1)
解:
(2)
∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
②
(3)
当点Q在点F的下方时,如图,
,DQ=DF+FQ=4+1=5(cm)
由(2)可知,
设
,
即
解得:
∴;
当当点Q在点F的上方时,如图,
cm,DQ =3cm,
由(2)可知,
设
,
即
解得:
∴.
【点睛】
本题主要考查矩形与折叠,正方形的性质、勾股定理、三角形的全等,掌握相关知识并灵活应用是解题的关键.
8.(2022·内蒙古赤峰)同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】如图①,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图③:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图④:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
【答案】(1)
(2)16
(3)或
【分析】(1)由正方形的性质可得,,根据ASA可证,由全等三角形的性质可得结论;
(2) 过点O作交AD于点M,交BC于点N,作交AB于点T,交CD于点R,证明△进而证明;
(3)分别求出,由勾股定理可得方程,求出x的值即可.
(1)
∵四边形ABCD是正方形,
∴∠
∵是对角线,
∴∠,
∴∠,
∵四边形是正方形,
∴∠,
∴∠
又∠
∴,
∴
∴
故答案为:
(2)
过点O作交AD于点M,交BC于点N,作交AB于点T,交CD于点R,如图,
∵点O是正方形ABCD的中心,
∴
又∠A=90°
∴四边形ATOM是正方形,
∴
同(1)可证△
∴
(3)
∵四边形均为正方形,
∴∠
∵CG在CD上,
∴
又CE在BC的延长线上,
∴
设则
在中,
在中,
延长AD,CE交于点Q,则四边形是矩形,
∴
∴,
在中,
若△为直角三角形,则有,
即
整理得,
解得,
∴或
【点睛】本题主要考查了正方形的性质,全等三角形的判定与性质,矩形的判定,勾股定理等知识,正确作出辅助线是解答本题的关键
题型三、正方形的动态问题
1.(2022·内蒙古通辽)已知点在正方形的对角线上,正方形与正方形有公共点.
(1)如图1,当点在上,在上,求的值为多少;
(2)将正方形绕点逆时针方向旋转,如图2,求:的值为多少;
(3),,将正方形绕逆时针方向旋转,当,,三点共线时,请直接写出的长度.
【答案】(1)2
(2)
(3)
【分析】(1)根据题意可得,根据平行线分线段成比例即可求解;
(2)根据(1)的结论,可得,根据旋转的性质可得,进而证明,根据相似三角形的性质即可求解;
(3)勾股定理求得,,进而根据,由相似三角形的性质即可求解.
(1)
正方形与正方形有公共点,点在上,在上,
四边形是正方形
(2)
如图,连接,
正方形绕点逆时针方向旋转,
,
(3)
如图,
,,
,,,
三点共线,
中,,
,
由(2)可知,
,
.
【点睛】本题考查了平行线分线段成比例,相似三角形的性质与判定,正方形的性质,勾股定理,旋转的性质,综合运用以上知识是解题的关键.
同课章节目录
