小学数学 人教版五年级数学上册《预习学案》(带答案)
文档属性
| 名称 | 小学数学 人教版五年级数学上册《预习学案》(带答案) | 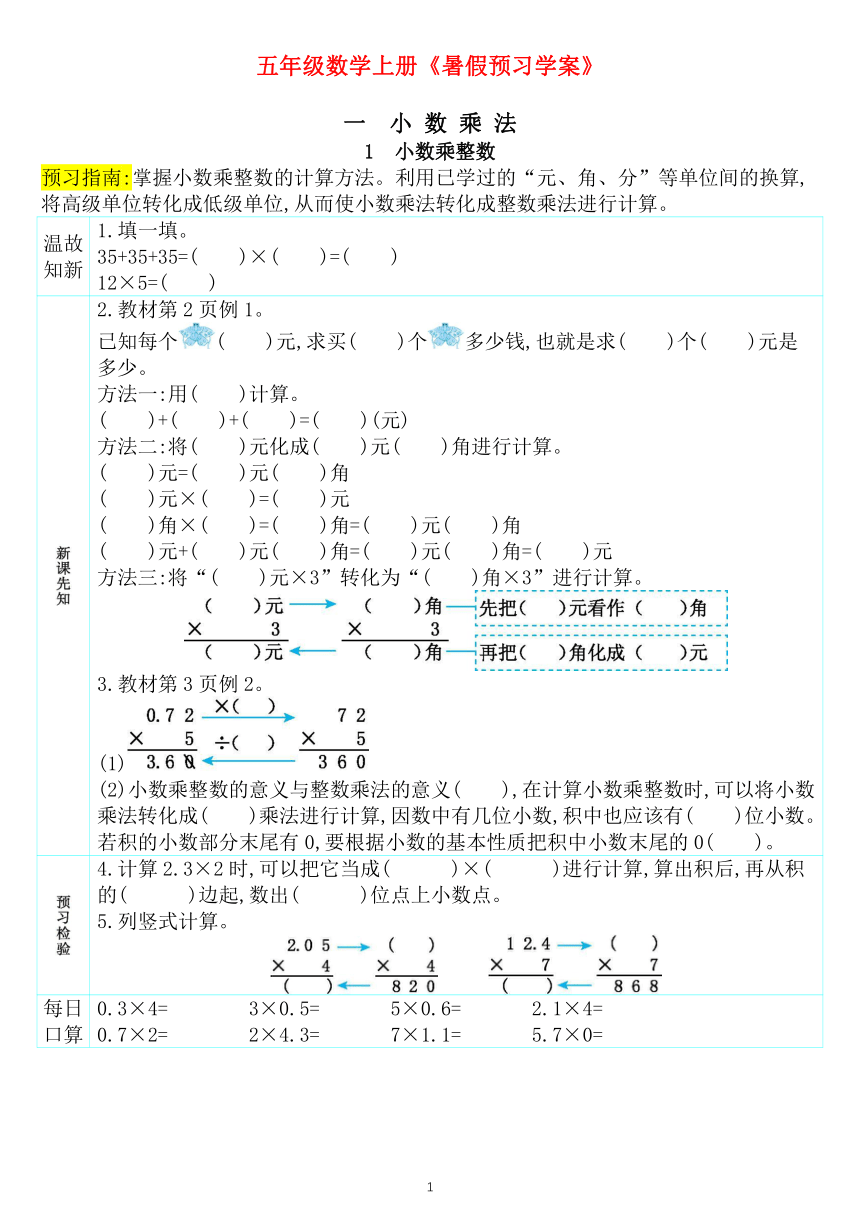 | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 10:47:20 | ||
图片预览




文档简介
五年级数学上册《暑假预习学案》
一 小 数 乘 法
1 小数乘整数
预习指南:掌握小数乘整数的计算方法。利用已学过的“元、角、分”等单位间的换算,将高级单位转化成低级单位,从而使小数乘法转化成整数乘法进行计算。
温故 知新 1.填一填。 35+35+35=( )×( )=( ) 12×5=( )
2.教材第2页例1。 已知每个( )元,求买( )个多少钱,也就是求( )个( )元是多少。 方法一:用( )计算。 ( )+( )+( )=( )(元) 方法二:将( )元化成( )元( )角进行计算。 ( )元=( )元( )角 ( )元×( )=( )元 ( )角×( )=( )角=( )元( )角 ( )元+( )元( )角=( )元( )角=( )元 方法三:将“( )元×3”转化为“( )角×3”进行计算。 3.教材第3页例2。 (1) (2)小数乘整数的意义与整数乘法的意义( ),在计算小数乘整数时,可以将小数乘法转化成( )乘法进行计算,因数中有几位小数,积中也应该有( )位小数。若积的小数部分末尾有0,要根据小数的基本性质把积中小数末尾的0( )。
4.计算2.3×2时,可以把它当成( )×( )进行计算,算出积后,再从积的( )边起,数出( )位点上小数点。 5.列竖式计算。
每日 口算 0.3×4= 3×0.5= 5×0.6= 2.1×4= 0.7×2= 2×4.3= 7×1.1= 5.7×0=
2 小数乘小数(1)
预习指南:掌握小数乘小数的计算方法。知道积的小数位数不够时,要在前面用0补足。
温故 知新 1.直接写出得数。 0.5×8= 1.1×7= 2.3×4= 0.01×10= 1.9×2= 2×3.3= 2×1.8= 3.3×3=
2.教材第5页例3。 已知宣传栏是长为( )m,宽为( )m的长方形,每平方米要用油漆( )kg。要求一共需要多少千克油漆,需先算出长方形宣传栏的( ),再乘( )得到一共需要的油漆的质量。 (1)先求长方形宣传栏的面积。
2.4×0.8= (cm2)
(2)再算需要多少千克油漆。
1.92×0.9= (kg)
(3)小数乘法的计算步骤。 ①先按照整数乘法算出积,再点( ); ②点小数点时,看( )中一共有几位小数,就从积的( )起数出几位,点上小数点。 (4)规范解答: 3.教材第6页例4。 乘得的积的小数位数不够时,要在前面用( )补足,再点小数点。
4.判断下面各个积的小数位数。 3.72×28( ) 3.72×0.28( ) 372×0.028( ) 5.列竖式计算。 1.8×2.3= 0.37×0.4= 1.06×25=
每日 口算 0.42×0.2= 1.4×0.7= 0.16×0.6= 1.2×0.5= 0.6×3.5= 0.8×1.25= 0.3×4.7= 3.1×0.02=
小数乘小数(2)
预习指南:正确解决倍数是小数的实际问题,根据数据的特点灵活选择验算方法。
温故 知新 1.直接写出得数。 12.5×0.8= 12.5×8= 0.25×4= 0.04×25= 0.13×2= 8×0.25= 0.06×50= 0.04×800=
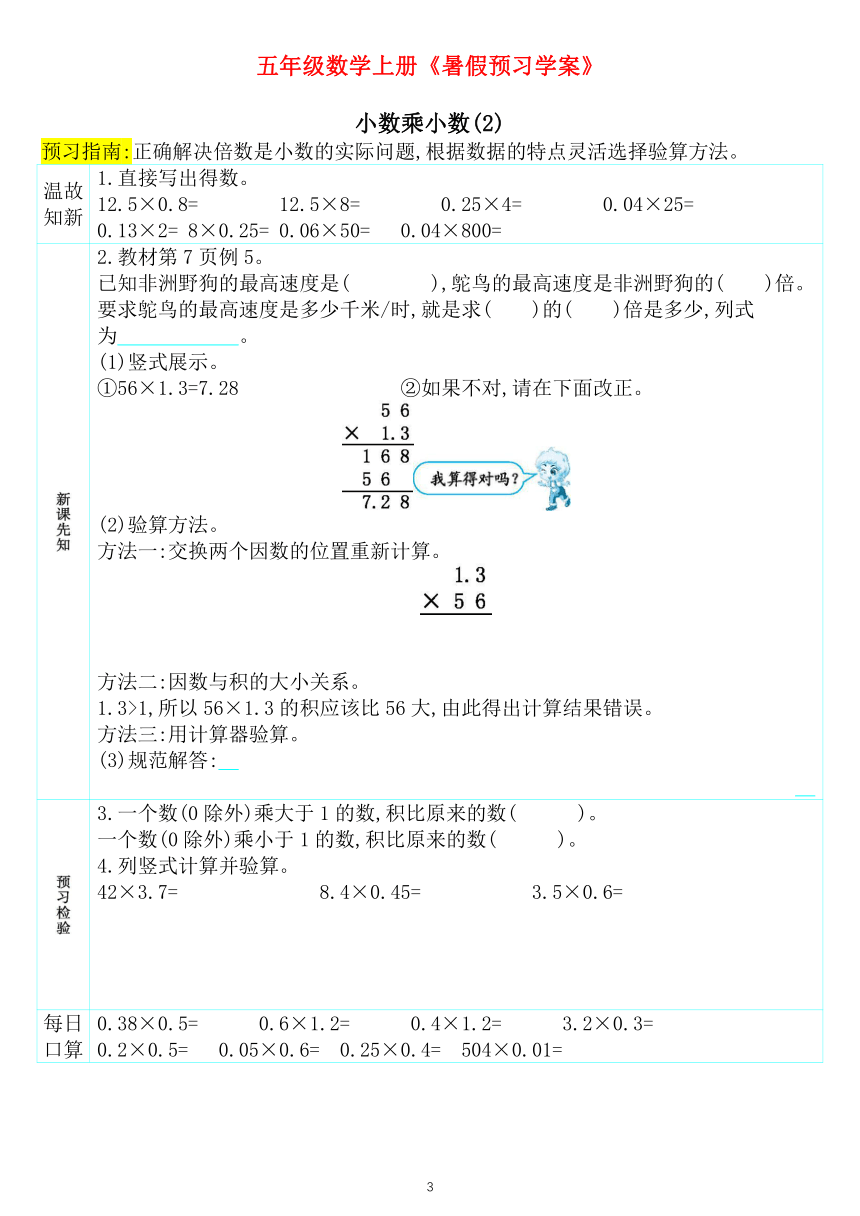
2.教材第7页例5。 已知非洲野狗的最高速度是( ),鸵鸟的最高速度是非洲野狗的( )倍。要求鸵鸟的最高速度是多少千米/时,就是求( )的( )倍是多少,列式为 。 (1)竖式展示。 ①56×1.3=7.28 ②如果不对,请在下面改正。 (2)验算方法。 方法一:交换两个因数的位置重新计算。 方法二:因数与积的大小关系。 1.3>1,所以56×1.3的积应该比56大,由此得出计算结果错误。 方法三:用计算器验算。 (3)规范解答:
3.一个数(0除外)乘大于1的数,积比原来的数( )。 一个数(0除外)乘小于1的数,积比原来的数( )。 4.列竖式计算并验算。 42×3.7= 8.4×0.45= 3.5×0.6=
每日 口算 0.38×0.5= 0.6×1.2= 0.4×1.2= 3.2×0.3= 0.2×0.5= 0.05×0.6= 0.25×0.4= 504×0.01=
3 积的近似数
预习指南:学会用“四舍五入”法取积的近似数。先算出准确数,再根据需要保留一定的小数位数;在求积的近似数时,小数末尾的0不能去掉,否则精确度就变了。
温故 知新 1.填表。 保留整数保留一位小数保留两位小数6.9343.9047.8685
2.教材第11页例6。 已知人的嗅觉细胞约有( )亿个,狗的嗅觉细胞个数是人的( )倍。求狗约有多少亿个嗅觉细胞,就是求( )的( )倍是多少,用( )计算,列式为 。 (1)要求得数保留一位小数,就是用( )法取积的近似数。 (2)列竖式计算。
(3)求积的近似数时,先确定( )的小数位数,再看需要保留数位的( ),用( )的方法取舍。近似数与准确数有区别,近似数应该用( )号连接。取积的近似数时,小数末尾的0( )(填“能”或“不能”)去掉。 (4)规范解答:
3.填空题。 (1)0.8×0.9的积是( ),得数保留一位小数,要看( )位上的( ),应( ),结果是( )。 (2)1.7×0.45的积是( ),精确到百分位,就要看( )位上的( ),应向( )位( )。结果是( )。 4.列竖式计算。(得数保留两位小数) 0.86×1.2≈ 2.34×0.15≈ 5.刘老师买25本《童话故事》,大约需要多少钱
每日 口算 10.5×0.1= 0.5×0.17= 6.5×0.2= 0.3×4.7= 1.8×0.3= 0.42×0.7= 0.25×0.4= 2×0.45=
4 整数乘法运算定律推广到小数
预习指南:掌握小数四则混合运算的运算顺序,理解整数乘法运算定律对于小数乘法同样适用,并能运用乘法运算定律进行简便计算。
温故 知新 1.计算。 25×95×4 25×32 4×48+6×48 102×56 2.用字母表示下列整数乘法运算定律。 乘法交换律: 乘法结合律: 乘法分配律:
3.教材第12页小天使。 观察下面每组中的两个算式,它们有什么关系 0.7×1.2○1.2×0.7 (0.8×0.5)×0.4○0.8×(0.5×0.4) (2.4+3.6)×0.5○2.4×0.5+3.6×0.5 通过观察、计算发现:整数乘法的运算定律在小数乘法中( ),运用这些定律可以使一些计算( )。 4.0.65×202,202接近( ),把这个数拆成( )的形式,再运用( )律简算。
5.用简便方法计算下面各题。 4.8×0.25 1.5×105 45.2×99 1.2×2.5+0.8×2.5 2.33×0.5×4
每日 口算 4.2×20= 1.2×0.09= 1.2×0.8= 1.07×0.6= 1.5×0.4= 0.2×5= 0.8×12.5= 0.2×5+0.5=
5 解决问题(1)
预习指南:能运用估算的知识解决实际问题。会用表格的形式整理信息,能根据实际问题和具体数据选择适当的估算策略。
温故 知新 1.估算。 76×89≈ 38×51≈ 102×18≈ 53×21≈
2.教材第15页例8。 (1)阅读与理解。 妈妈买了( )袋大米和( )kg肉,还想买( )盒鸡蛋。要想知道剩下的钱够不够,只要把买到的所有商品的价格加在一起,与( )元进行比较,可以用估算的方法解决。用表格表示妈妈买的东西,如下: 单价数量总价大米—肉—鸡蛋—
(2)分析与解答。 小亮:1袋大米不到31元,2袋不到( )元;肉不到27元;买一盒10元的鸡蛋,总共不超过( )元,够了。 小丁:1袋大米超过30元,2袋超过( )元;1 kg肉超过25元,0.8 kg也就超过( )元;再买一盒20元的鸡蛋,总共就超过了( )元,不够。 (3)回顾与反思。 小亮和小丁的方法有什么不同 小亮是通过把物品的钱数( ),发现( )后的总钱数不超过100元,判断出“够买”。 小丁是通过把物品的钱数( ),发现( )后的总钱数等于100元,所以总钱数超过了100元,判断出“不够买”。
3.王阿姨买4 kg香蕉和6 kg苹果,已知香蕉每千克2.8元,苹果每千克3.9元。王阿姨付50元,够吗 4.小明带100元去超市购物,他买了4本《故事书》和2盒彩笔,剩下的钱还够买2个文具盒吗
每日 口算 0.2×8.1= 0.8×1.5= 3.5×0.2= 1.6×0.5= 4.5×0.6= 3.6×0.02= 0.25×0.4= 4.8×0.02=
解决问题(2)
预习指南:有条理地整理题中有用的信息,能准确地找到分段计费问题的数量关系,运用分段计算的方法正确解答这类实际问题。
温故 知新 1.计算。 8+3.4×5 6.5-0.8×3.2
2.教材第16页例9。 (1)阅读与理解。 已知出租车的收费标准是3 km以内( )元;超过3 km的部分,每千米( )元(不足1 km按1 km计算)。行驶6.3 km,要按( )km计算付多少钱。 (2)分析与解答。 方法一:分段计算法。
前面3 km应收( )元,后面4 km按每千米( )元计算。
列式为 方法二:假设调整法。
先按每千米( )元算出( )km需要的钱数,再加上前3 km少算的钱数。
列式为 (3)回顾与反思。 制作10 km以内出租车价格表,对照价格表检验计算结果是否正确。 行驶的里程/km12345678910出租车费/元
4. 5.某地拨打市内电话前3分钟内0.22元,超过3分钟,每分钟收费0.11元(不足1分钟按1分钟算)。妈妈一次市内通话的时间是7分36秒,她这一次通话的费用是多少
每日 口算 0.2×50= 12.5×4= 0.4×1.7= 1.1×0.1= 0.5×0.5= 100×0.6= 2.8×3= 0.85×0.2=
6 解 决 问 题
预习指南:会用“进一法”和“去尾法”取商的近似数。在解决问题的过程中能根据具体问题确定取商的近似数的方法。
温故 知新 1.填空。 (1)3.25×0.17的积是( )位小数,保留两位小数是( )。 (2)1.85÷0.9的商保留两位小数约是( ),精确到十分位约是( )。
2.教材第39页例10(1)。 (1)阅读与理解。 已知分装2.5 kg香油,每个瓶子最多可盛0.4 kg。求需要准备几个瓶子,就是求( )里面有几个0.4,用除法计算,列式为 。 (2)分析与解答。 2.5÷0.4的计算结果是( ),瓶子不能有0.25个,应该取整数,用“四舍五入”法取近似数是6,但是6个瓶子只能装( )kg,还剩下( )kg,因此需要准备( )个瓶子。 (3)规范解答: 3.教材第39页例10(2)。 (1)阅读与理解。 已知每个礼盒要用1.5 m长的丝带,求25 m长的红丝带可以包装多少个礼盒,就是看( )里面有多少个( ),用除法计算,列式为 。 (2)分析与解答。 25÷1.5的计算结果是( )。盒子数不能是0.666…个,用“四舍五入”法取近似数是17,但是包装17个礼盒需要( )m长的红丝带,还差( )m,所以最多只能包装( )个礼盒。 (3)规范解答: (4)回顾与反思。 一般用“四舍五入”法取商的近似数,但是在解决实际问题时,要根据实际需要,用( )法或( )法取商的近似数。
4.结合生活实际,求出下面各题的近似数,并填在括号里。 (1)一块布料可以做5.8件同样的衣服,实际只能做( )件。 (2)一堆水泥,一辆汽车需要5.4次运完,实际需要运( )次。 (3)亮亮的零花钱可以买7.9支钢笔,实际可以买( )支钢笔。 5.一辆小汽车可以坐5人,五(2)班一共有38名学生准备去春游,需要准备多少辆这样的小汽车
每日 口算 2.8÷14= 8.1÷2.7= 50.8÷2= 4÷0.8= 5×0.6= 1.2÷0.3= 4÷0.4= 93÷3.1=
二 位 置
位 置
预习指南:明确行和列的意义,掌握用数对表示物体位置的方法。
温故 知新 1.教室里,你的座位在第( )排第( )列(根据自己班的情况填写)。通常我们把竖排叫做( ),横排叫做( )。
2.教材第19页例1。 (1)确定第几列,一般是从( )往( )数;确定第几行,一般是从( )往( )数。用数对表示位置时, ( )在前,( )在后,中间用( )隔开,最后用括号括起来。 (2)张亮在第2列、第3行的位置,可以用数对( , )表示。 (3)王艳同学的位置用数对表示是( , ),赵雪同学的位置用数对表示是( , ),看一看有什么不同。 (4)王乐同学的位置用数对表示是(6,4)是在第( )列、第( )行,在图上指出哪个是王乐同学。 3.教材20页例2。 (1)用数对(3,0)表示大门的位置,说明大门所在的位置对应的列数是( ),行数是( )。 (2)熊猫馆的位置是( , ),大象馆的位置是( , ),猴山的位置是( , ),海洋馆的位置是( , )。 (3)请在右图中标出下面场馆的位置。 飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3) (4)确定物体的位置时,先找到( ),再找到( ),最后描点标明。
4.小军坐在教室的第3列第4行,用数对表示为( , ),用数对(5,2)表示的某同学坐在第( )列第( )行的位置。 5.(1)用数对写出三角形各个顶点的位置。 A( , ) B( , ) C( , ) (2)将三角形向右平移4格,再向上平移3格后得到新图形三角形A'B'C'。画出新的三角形,并用数对表示新的三角形的三个顶点的位置。 A': ,B': ,C': 。
每日 口算 2.6×0.03= 1.8×0.04= 0.9×12= 30×2.5= 5.1×4= 41×50= 1.11×2= 1.03×0.2=
三 小 数 除 法
1 除数是整数的小数除法
预习指南:掌握除数是整数的小数除法的计算方法。理解商的小数点和被除数的小数点对齐的道理。
温故 知新 1.列竖式计算。 2145÷15= 416÷32= 1380÷15=
2.教材第24页例1。 (1)已知王鹏计划4周跑步22.4 km,求王鹏平均每周应跑多少千米,用( )法计算,列式为 。 (2)计算方法。 方法一:利用单位改写计算。 22.4 km=( )m ( )÷( )=( )m ( )m=( )km 方法二:列竖式计算。 (3)规范解答: 3.教材第25页例2。 (1)已知王鹏的爷爷计划16天慢跑28 km,求平均每天慢跑多少千米,用( )法计算,列式为 。 (2)列竖式计算。 除数是整数的小数除法,先按照( )除法的方法计算,( )的小数点要和( )的小数点对齐。哪一位不够商1,就在那一位上写( )占位。如果除到被除数的末尾仍有余数,要添上( )继续除。 (3)规范解答: 4.教材第25页例3。 (1)已知王鹏每周计划跑5.6 km,求平均每天要跑多少千米,用( )法计算,列式为 。
(2)列竖式计算。 (3)规范解答:
5.列竖式计算。 7.83÷9= 43.5÷29= 14.21÷7= 1.35÷15= 6.文具商店。 (1)玲玲买了2块橡皮,一共花了2.4元。你能求出每块橡皮多少钱吗 (2)一套尺子的价钱是一个圆规价钱的多少倍
每日 口算 2.4÷4= 4.2÷7= 8.4÷6= 6.8÷2= 3.9÷13= 3.6÷12= 8.1÷27= 6.8÷4=
2 一个数除以小数
预习指南:理解将“一个数除以小数”转化成“一个数除以整数”的算理。知道如果除数是小数,要先把除数变成整数,被除数的小数点移动位数与除数的相同。
温故 知新 1.把20.09扩大到它的100倍是( );0.006去掉小数点后是( ),结果( )到原来的( )。 2.在括号里填上适当的数。 13.3÷0.4=( )÷4 3.72÷1.2=( )÷12
3.教材第28页例4。 (1)已知编一个“中国结”要用0.85 m丝绳,求这些丝绳可以编几个“中国结”,就是求( )里面有几个( ),用( )法计算,列式为 。 (2)计算方法。 方法一:单位转化法,把“米”转化成“厘米”计算。 7.65 m=( )cm 0.85 m=( )cm 因为765÷85=9,所以7.65÷0.85=( )。 方法二:列竖式计算。 把0.85扩大到它的( )倍,是( ),为了使商不变,7.65也扩大到它的( )倍,变成( ),因此就把7.65÷0.85转化成了( )÷( ),商是( )。 (3)规范解答: 4.教材第29页例5。 12.6÷0.28= (1)把0.28扩大到它的( )倍,是( ),为了使商不变,12.6也扩大到它的( )倍,因为12.6是一位小数,根据( )的性质,在它的末尾用( )补足,再把小数点向右移动( )位。 (2)计算一个数除以小数时, ①先移动( )的小数点,使它变成( ); ②( )的小数点向右移动几位,( )的小数点也向右移动几位(位数不够的,在被除数的末尾用 补足); ③然后按除数是( )的小数除法进行计算。
5.列竖式计算。 5.98÷0.23= 197.6÷5.2= 10.8÷4.5=
每日 口算 1.6÷0.8= 7.2÷0.8= 7.8÷6= 0.48÷0.04= 6.4÷8= 2.4÷0.3= 0.88÷0.8= 4.5÷9=
3 商的近似数
预习指南:学会用“四舍五入”法求商的近似数。求近似数时,先看保留几位小数,就除到比需要的小数位数多一位,再用“四舍五入”法取近似数。
温故 知新 1. 用“四舍五入”法求下面各小数的近似数。 保留整数保留一位小数保留两位小数0.98814.49893.0924
2.教材第32页例6。 (1)已知12个羽毛球19.4元,求每个羽毛球大约多少钱。根据“单价=( )÷( )”可知,用( )计算,列式为 。 (2)列竖式计算。 ①保留两位小数:19.4÷12≈( )(元),要看小数部分第( )位上的数。计算价钱,保留两位小数,表示精确到( )。 ②保留一位小数:19.4÷12≈( )(元),要看小数部分第( )位上的数。计算价钱,保留一位小数,表示精确到( )。 (3)在计算小数除法需要求商的近似数时,一般除到比需要保留的小数位数多( )位,再按照( )法取商的近似数。保留小数位数,需要连续进位时,近似数末尾的0( )(填“能”或“不能”)去掉。 (4)规范解答:
3.列竖式计算,按要求取商的近似数。 48÷2.3≈ 1.55÷3.8≈ 3.81÷7≈ (保留一位小数) (保留两位小数) (精确到百分位)
每日 口算 0.9÷0.45= 3.9÷0.13= 80÷0.4= 50÷20= 6.9÷3= 3.6÷6= 3.2÷8= 9.1÷7=
4 循 环 小 数
预习指南:认识循环小数,能正确运用循环小数表示商。能用简便记法表示循环小数,知道循环小数一定是无限小数,无限小数不一定是循环小数。
温故 知新 1.列竖式计算。(结果保留两位小数) 4÷7≈ 16÷3≈ 2÷9≈
2.教材第33页例7。 (1)已知跑400 m用了75秒,求平均每秒跑多少米。根据“速度=( )÷( )”可知,用( )法计算,列式为 。 (2)列竖式计算。 列竖式计算时,每次除得的余数都是“( )”,商的小数部分总是重复出现“( )”。 (3)规范解答: 3.教材第33页例8。 (1)用竖式计算28÷18时,每次除得的余数都是“( )”,商的小数部分总是重复出现“( )”。 (2)用竖式计算78.6÷11时,除得的余数“( )”和“( )”重复出现,商的小数部分中“( )”和“( )”重复出现。 (3)一个数的小数部分,从某一位起,一个数字或者几个数字依次不断( )出现,这样的小数叫做( )小数。依次不断( )出现的数字,就是这个循环小数的( )。 (4)循环的数字只有一个的循环小数,可以只写一个循环的数字,并在这个数字的上面记一个圆点。例如:5.333…写作( );循环的数字是多个的循环小数,可以只写第一组循环的数字,并在这组数字的首位和末位的数字上面各记一个圆点。例如:0.203203…写作( )。 (5)小数部分的位数有限的小数叫( )小数,小数部分的位数无限的小数叫( )小数。
4.把下面的小数保留三位小数。 7.3≈ 5.≈ 3.6464≈ 5.在○里填上“>”“<”或“=”。 0.○0.444 2.○2.1 1.0○1.
每日 口算 3.5÷5= 4.2÷7= 9.6÷16= 4.5÷5= 1.8÷30= 0.28÷0.7= 90÷0.9= 0.88÷0.8=
5 用计算器探索规律
预习指南:能根据计算器计算的结果发现规律,并利用规律解决有关问题。
温故 知新 1.按规律填数。 (1)1,1.1,1.3,1.6,( )。 (2)0.81,0.64,0.49,0.36,( ),( )。
2.教材第35页例9。 (1)先计算出3÷11,4÷11,5÷11的得数。 3÷11=( ) 4÷11=( ) 5÷11=( ) (2)比较发现规律。 1÷11=0.0909…,商的循环节是( )。 2÷11=0.1818…,商的循环节是( )。 3÷11=( ),商的循环节是( )。 4÷11=( ),商的循环节是( )。 5÷11=( ),商的循环节是( )。 发现商的规律: 都是循环小数; 整数部分都是0; 循环节都是被除数的( )倍。 (3)根据发现的规律直接写出下面各题的商。 6÷11=( ) 7÷11=( ) 8÷11=( ) 9÷11=( ) (4)用计算器探索规律的方法:用计算器( )→观察发现( )→根据( )写结果。在寻找规律时,不仅要观察( ),还要观察( ),对比各自的特点,找到它们内在的联系,从而总结出规律。
3.根据规律填数。 (1)3,3.3,3.33, , , 。 (2)0.,0.,0., , , 。 (3)1.2,11.22,111.222, , , 。 4.运用规律直接写出下面三题的得数。 1÷9=0.111… 2÷9=0.222… 3÷9=0.333… 4÷9= 5÷9= 7÷9= 5.不计算,运用规律直接填出得数。 6×7=42 6.6×6.7=44.22 6.66×66.7=( ) 6.666×666.7=( )
每日 口算 0.23×0.2= 4.8÷0.16= 10÷0.2= 2.4÷0.3= 36÷0.12= 45÷1.5= 75÷0.25= 93÷3.1=
四 可 能 性
可 能 性
预习指南:感受随机事件发生的确定性和不确定性。能准确判断事件发生的可能性的大小。
温故 知新 1.任意抛一枚硬币,落地后,( )正面朝上,也( )反面朝上。(填“可能”或“不可能”)
2.教材第44页例1。 三张卡片上分别写着唱歌、跳舞、朗诵。 (1)小明可能抽到( ),也可能抽到( ),还可能抽到( )。有( )种可能。 (2)小明抽到了跳舞后,还剩下两张卡片,所以小丽可能抽到( ),也可能抽到( )。有( )种可能。 (3)小丽抽到朗诵后,只剩下一张卡片,所以小雪( )抽到唱歌。 (4)在一定的条件下,一些事件的结果是可以预知的,具有( )性,( )的事件用“( )”或“( )”来描述事件的结果。一些事件的结果是不可预知的,具有( )性,( )的事件用“( )”来描述事件的结果。 3.教材第45页例2。 (1)盒子里有( )种颜色的棋子,任意摸出一个棋子,可能是( )色,也可能是( )色,有( )种可能性。 (2)左边的小组摸出红色的棋子( )次,摸出蓝色的棋子( )次。 (3)右边的小组摸出红色的棋子( )次,摸出蓝色的棋子( )次。 (4)无论怎么摸,摸出( )色棋子的次数比( )色棋子的次数多。从而发现,事件发生的可能性有大有小,在总数中所占的数量越多,可能性就越( );所占数量越少,可能性就越( )。 4.教材第46页例3。 (1)盒子里有( )种颜色的球,任意摸出一个球,可能是( )色,也可能是( )色,有( )种可能性。 (2)观察记录表。 每个小组摸到( )球的次数多,摸到( )球的次数少,说明盒子里的( )球被摸到的可能性要大于( )球。 由此可知,盒子里( )球多,( )球少。从而发现,事件发生的可能性的大小与( )有关,事件发生的可能性越大,那么在总数中所占的数量就( );事件发生的可能性越小,所占数量越( )。
5.把2个绿球和3个红球(除颜色不同外其他完全相同)放入箱中,任意摸一个球,有( )种结果,摸到( )的可能性大。再放进4个黄球,有( )种结果,摸到( )的可能性大,( )摸到蓝球。
每日 口算 3.5×2= 0.2÷0.1= 0.24×5= 3.2÷8= 4.2×0.5= 1.2÷0.3= 0.5×100= 7.2÷9=
五 简 易 方 程
1 用字母表示数(1)
预习指南:能用字母表示数和数量关系,理解字母的取值范围,知道字母与数字相乘的简便写法,并会求含有字母的式子的值。
温故 知新 1.生活中,用字母CCTV表示( )。 扑克牌中,A、K、J、Q这些字母表示的数分别是( )。
2.教材第52页例1。 (1)根据“爸爸比小红大30岁”可知:当小红1岁时,爸爸的年龄是1+30=31(岁);当小红2岁时,爸爸的年龄是2+30=32(岁);当小红3岁时,爸爸的年龄是3+30=33(岁)……列表表示为 (2)用一个式子表示任何一年爸爸的年龄的方法。 方法一:用关系式表示。 根据“爸爸比小红大30岁”可以知道:爸爸的年龄=( )的年龄+( )岁。 方法二:用含有字母的式子表示。 如果用字母a表示小红的年龄,那么爸爸的年龄就可以用( )表示。 这里的a不能无限大,也不能是分数、小数等。 (3)代入求值:当a=11岁时,爸爸的年龄是( )岁。 3.教材第53页例2。 (1)根据“在月球上,人能举起物体的质量是地球上的6倍”可知:当人在地球上能举起1 kg的物体时,在月球上就能举起1×6=6(kg)的物体;当人在地球上能举起2 kg的物体时,在月球上就能举起2×6=12(kg)的物体……列表表示为
(2)用含有字母的式子表示人在月球上能举起物体的质量。 人在月球上能举起物体的质量=人在( )上能举起物体的质量×( ),如果用字母x表示人在地球上能举起物体的质量,那么人在月球上能举起物体的质量可表示为( )。这里的x应该是一个大于0而小于或等于人在地球上所能举起的极限质量。字母和数字相乘,乘号省略不写,一般把数写在字母的( )面。 (3)代入求值:当x=15时,图中小朋友在月球上能举起的物体的质量是( )kg。
4.填一填。 (1)阳光小学五年级有学生178人,星期三缺勤的有a人,出勤的有( )人。 (2)一箱苹果重20千克,b箱苹果重( )千克。 5.用含有字母的式子表示出x只青蛙的腿的数量是( ),当x=12时,这些青蛙有( )条腿。 6.你能用式子表示下面三角形的周长吗 (1)三角形的三条边分别长a、b、c。 (2)一个等腰三角形,底长a,一条腰长b。
每日 口算 1.5×4= 0.45÷0.15= 0.49÷7= 84÷4.2= 3.62×2= 0.2÷0.1= 0.24×5= 3.2÷8=
用字母表示数(2)
预习指南:能用字母表示运算定律及计算公式,理解一个数的平方的含义,知道乘号可以简写和略写,会代入公式计算。
温故 知新 1.省略乘号写出下列各式。 4×b= x×5= a×m= c×3= y×y= 2.(1)用v表示速度,t表示时间,s表示路程。s=( ) (2)乐乐每分钟走80 m,30分钟能走多少米
3.教材第54页例3。 (1)用字母表示运算定律。 运算定律用字母表示简便记法加法交换律—加法结合律—乘法交换律乘法结合律乘法分配律
(2)用字母表示计算公式。 ①如果用a表示正方形的边长,用S表示面积,用C表示周长。 正方形的周长公式用字母表示为( ),面积公式用字母表示为( )。a2读作( ),表示( )个( )相( )。 ②代入求值:当a=6时,计算正方形的周长和面积: C=( )=( )×( )=( )(cm) S=( )=( )×( )=( )(cm2)
4.根据运算定律在 里填上适当的数或字母。 (x+37)+63=x+( + ) (a+6)×b= · + · 2.4×a+b×2.4=( + )× 9x-5x=( - )x 5.先写出长方形的周长和面积计算公式,再计算。
每日 口算 8÷0.5= 0.32÷16= 0.5×1.1= 6÷1.2= 0.4÷8= 6.8÷1.7= 14÷0.7= 0.49÷0.7=
用字母表示数(3)
预习指南:用含有字母的式子表示数量关系,并能化简含有字母的式子。
温故 知新 1.把结果相同的两个式子连起来。 a2 4.5×4.5 x+x b×1 2x b 4.52 a×a
2.教材第58页例4。 (1)根据题意可以得到下面的数量关系式: 一大杯果汁的质量( )=还剩下果汁的质量 (2)每小杯果汁是x g,3小杯果汁是( )g,1大杯果汁是( )g,倒去3小杯果汁后,还剩下( )g。 (3)当x=200时,大杯中还剩下( )g果汁。1200-3x的差最小是( ),3x最大是( ),所以式子中x的值最大是( )。 3.教材第59页例5。 (1) (2)从上面两种数小棒的方法中可以得出:3x+4x=( )。 (3)当x=8时,一共用( )根小棒。
4.公园里有松树x棵,柳树的棵数比松树的5倍少8棵。 (1)用式子表示柳树的棵数。 (2)当x=25时,柳树有多少棵 5.用6根小棒摆1个平行四边形,5根小棒摆1个梯形。 (1)摆x个平行四边形和x个梯形,
一共用了多少根小棒 (2)当x=15时,一共用了多少根小棒
每日 口算 0.63÷9= 1.8×0.4= 26.5÷5= 3.1×0.3= 9÷5= 3.2÷1.6= 2.4×8= 7.6÷3.8=
2 方程的意义和等式的性质(1)
预习指南:理解方程的意义并会判断一个式子是否为方程。知道方程与等式的关系,并能用方程表示简单的数量关系。
项目 内容
温故 知新 1.填空。 20y-8y=( ) 17.5x-7.5x=( ) b-0.35b=( ) 6a+15a-3a=( )
2.教材第62页情境图。 (1)认识等式。 (2)认识方程。 ①空杯子的质量。 ②称一杯水的质量。 如果水重x g,那么杯子和水共重( )g;此时天平左边重,用式子表示为( )。天平右边增加一个100 g砝码,此时天平左边重,用式子表示为( );天平右边再增加一个100 g砝码,此时天平右边重,用式子表示为( );把一个100 g的砝码换成50 g,此时天平平衡,用式子表示为( )。
3.教材第63页情境图。 (1)每本练习本x元,3本练习本的总价可以表示为( )元,也就是2.4元,因此可列等式为( )。 (2)像100+x=250,3x=2.4……这样,含有( )的( )就是( )。判断一个式子是不是方程,一看是不是( ),二看有没有( )。 (3)你能自己写出一些方程吗
4.下面哪些式子是方程 在后面的括号里画“ ”。 x+3.6=7( ) a×2<2.4( ) 3-1.4=1.6( ) 3÷b( ) 8-x=2( ) 6.2÷2>3( ) 4×2.4=9.6( ) 2x+3y=9( ) 5.用方程表示下面的数量关系。
每日 口算 1.21÷11= 8.5÷1.7= 0.36÷4= 0.75×4= 53×0.01= 0.12×0.7= 0.92÷0.4= 0.32÷1.6=
方程的意义和等式的性质(2)
预习指南:理解等式的性质。
温故 知新 1.判断。(正确的画“ ”,错误的画“ ”) (1)含有未知数的式子叫做方程。 ( ) (2)所有的方程都是等式。 ( ) (3)2x-3=0不是方程。 ( )
2.教材第64页情境图。用含有字母的式子表示下面的数量关系。 (1) 1把茶壶的质量等于2个茶杯的质量,用等式表示为( ),在天平两边各增加1个同样的茶杯,天平仍然保持( ),用等式表示为( )。 (2) 1个花盆和1个花瓶的质量等于4个花瓶的质量,用等式表示为( ),在天平两边都拿掉1个花瓶,天平仍然保持( ),用等式表示为( ),即( )个花盆和( )个花瓶同样重。 (3)等式的性质1:等式两边( )或( )同一个数,左右两边仍然( )。 3.教材第65页情境图。用含有字母的式子表示下面的数量关系。 (1) 1瓶墨水的质量等于1个文具盒的质量,用等式表示为( ),左右两边的数量都扩大到原来的2倍,天平仍然保持( ),用等式表示为( )。 (2) 2个排球和6个皮球的质量相等,用等式表示为( ),将左右两边的球都平均分成2份,各去掉1份,天平仍然保持( ),用等式表示为( )。 (3)等式的性质2:等式两边乘同一个数,或除以同一个不为( )的数,左右两边仍然( )。
4.如果a=b,根据等式的性质填空。 a+6=b+( ) a-( )=b-8 a×2=b×( ) a÷( )=b÷3 a+c=b+( ) a×( )=b×c
每日 口算 1.44÷12= 18.2÷9.1= 4.5÷0.5= 8.1÷2.7= 2÷0.05= 3.2×0.2= 1.8×40= 4.27×0.1=
3 解方程(1)
预习指南:能运用等式的性质解方程,会正确解形如x±a=b、ax=b(a不等于0)、x÷a=b(a不等于0)、a-x=b、a÷x=b的方程。
温故 知新 1.如果x=y,根据等式的性质填空。 x-( )=y-a x+8=y+( ) x÷( )=y÷3.5 x×( )=y×c
2.教材第67页例1。 (1)一共有9个球,盒子里有x个,盒子外有3个。根据题意列方程为( )。 (2)根据等式的性质1,等式两边减去( ),左右两边仍然相等。天平演示: (3)规范书写。 x+3=9 解:x+3-( )=9-( ) 依据( ) x=( ) (4)使方程左右两边相等的( )的值,叫做方程的( )。求方程的解的过程叫做( )。方程的解是一个( ),而解方程是一个( )。 (5)检验。
方程左边=x+3
=( )+3
=( )
=方程右边
所以,( )是方程的解。 检验方法:把x的值代入方程的
( )边,然后检验方程的左
右两边的结果是否( ) 3.教材第68页例2。
3x=18
解:3x÷( )=18÷( ) 依据( )
x=( ) 4.教材第68页例3。
20-x=9
解:20-x+( )=9+( ) 依据( )
20=9+x
9+x=20
9+x-( )=20-( ) 依据( )
x=( )
5.解方程。 x+3.2=4.6 5x=6 18-x=3
每日 口算 10÷2.5= 0.3÷0.06= 0÷0.31= 4.2×4= 1.6×0.5= 0.12÷4= 9÷4.5= 0.24÷12=
解方程(2)
预习指南:把“ax”和“x±b”看成一个整体,解形如ax±b=c(a不等于0)和a(x±b)=c(a不等于0)的方程。
温故 知新 1.解方程。 2.4x=6 x-1.8=4 5.7÷x=3
2.教材第69页例4。 (1)已知1盒铅笔有x支,由题意列等量关系式为3盒铅笔的支数+( )支=( )支,列方程为( )。 (2)把3x看成一个整体,根据等式的性质1,在等式的两边同时减去( ),得到3x=( ),再根据等式的性质2解方程。 3x+4=40
解:3x+4-( )=40-( )依据( )
3x=36
3x÷( )=36÷( )依据( )
x=( ) 检验:
方程左边=3x+4
=
=
=
所以,x=( )是方程的解。 3.教材第69页例5。 2(x-16)=8 解: 2(x-16)÷( )=8÷( ) 把( )看作一个整体。 x-16=4 x-16+( )=4+( ) x=( ) 也可以这样解: 2(x-16)=8
解:2x-32=8 运用了( )律
2x-32+( )=8+( )
2x=40
2x÷( )=40÷( )
x=( )
4.根据题意列方程并求出方程的解。 (1) (2)
每日 口算 90÷4.5= 21.3×3= 0.1÷2= 0.21×4= 0.4×5= 1.4÷0.7= 1.6÷0.2= 4.8÷8=
4 实际问题与方程(一)
预习指南:能根据题中的等量关系列方程解决实际问题。知道列方程解决实际问题的步骤。
温故 知新 1.解方程。 x+19=51 2x=16.2 9x+36=72
2.教材第73页例1。 (1)已知小明的跳远成绩为4.21 m,超过原纪录0.06 m。由于原纪录是未知数,可以把它设为x m。 (2)根据题意写出数量关系式:( )+( )=( )。 (3)解:设学校原跳远记录是x m。 x+0.06=4.21 x+0.06-0.06=4.21-0.06 x=( ) 求出的未知数后面( )单位名称。(填“写”或“不写”) (4)检验。 方程左边=x+0.06 =( )+0.06 =( ) =方程右边 所以,( )是方程的解。 3.教材第74页例2。 (1)根据题意写出等量关系式:( )色皮的块数×2-4=( )色皮的块数。 (2)解:设共有x块黑色皮。 2x-4=20 2x-4+4=20+4←把( )看成一个整体。 2x=24 2x÷2=24÷2 x=( ) 答:共有( )块黑色皮。 (3)列方程解决实际问题的步骤: ①找出( ),用字母( )表示; ②分析实际问题中的( )关系,找出( )关系,列( ); ③( )并( )作答。
4.共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒
每日 口算 8.8÷0.2= 8.8×0.1= 1.08×1= 4÷0.5= 2÷0.4= 0.88÷0.44= 30÷0.15= 1.01×2=
5 实际问题与方程(二)
预习指南:理解实际问题中有关和、差、倍的数量关系,体验化归方法,选择合适的等量关系设未知数列方程。
温故 知新 1.解方程。 3x+4×2.5=46 x+2.5x=17.5 9x+11x=100
2.教材第77页例3。 (1)根据等量关系式“( )的总价+( )的总价=总价钱”列方程求解。 解:设苹果每千克x元。 2x+2.8×2=10.4
=
=
=
= 把2x看成一个整体,
求出方程的解 答: 。 (2)根据等量关系式“两种水果的单价和×2=总价钱”列方程求解。 解:设苹果每千克x元。 (2.8+x)×2=10.4
=
=
=
= 把x+2.8看成一个整体,
求出方程的解 答: 。 3.教材第78页例4。 (1)列出等量关系式:( )面积+( )面积=地球表面积。 (2)解:设( )面积为x亿平方千米,那么( )面积可以表示为2.4x亿平方千米。 x+2.4x=5.1 (1+2.4)x=5.1←运用了( )律 3.4x=5.1 3.4x÷3.4=5.1÷3.4 x=( ) 海洋面积:5.1-( )=( )(亿平方千米) 或2.4×( )=( )(亿平方千米) 答:陆地面积为 亿平方千米,海洋面积为 亿平方千米。
4.解决问题。 (1)一辆卡车今天计划运35吨货物,每次能运5吨。上午运了3次,下午要运几次才能运完 (2)妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和妈妈今年各多少岁
每日 口算 0.56×100= 9.5÷0.95= 7.2÷0.08= 12.8÷4= 3.2÷8= 7.2÷9= 84÷2= 72×0.01=
6 实际问题与方程(三)
预习指南:学会用画线段图等方法分析数量关系,用方程解决工程问题、行程问题、购物问题等一系列的实际问题,体会数学模型思想。
温故 知新 1.解方程。 5(x+1.5)=17.5 8(x-6.2)=41.6 6x+35×6=360
2.教材第79页例5。 (1)阅读与理解。 已知小林骑车的速度是( )米/分、小云骑车的速度是( )米/分,两家相距( )km,周日早上9:00两人分别从家骑自行车相向而行,求两人何时相遇。 (2)分析与解答。 ①画线段图,分析数量关系。 列出等量关系式:( )骑的路程+( )骑的路程=总路程。 ②列方程解决问题。 解:设( )。 0.25x+0.2x=4.5 0.45x=4.5←运用了( )律 0.45x÷( )=4.5÷( ) x=( ) 答:两人( )相遇。 (3)回顾与反思。 解决相遇问题时,可以先画( )分析数量之间的相等关系,再根据“相遇时间=( )÷( )”列方程解决。
3.解决问题。 (1)甲、乙两个工程队铺一条长1400 m的公路,他们从两端同时施工, 甲每天铺80 m,乙每天铺60 m,几天后能够铺完这条公路 (2)甲、乙两辆汽车同时从同一地点出发,相背而行,2.4小时后相距216千米。甲车的速度是42千米/时,求乙车的速度。
每日 口算 3÷0.05= 0.21÷0.7= 0.42÷10= 4.2÷0.7= 7.2÷0.4= 11÷0.1= 18÷0.2= 15÷0.5=
六 多边形的面积
1 平行四边形的面积
预习指南:利用数方格和割补法探索平行的四边形面积计算公式,并能正确计算。
温故 知新 1.画出下面平行四边形底边上的高。
2.教材第87页情境图。 要比较两个花坛的大小,需要先求出两个花坛的( )。观察花坛,一个是( )形,可以通过测量( )、( )计算出面积;一个是( )形,面积计算方法未知。 (1)数方格:一个方格代表1 m2,不满一格的都按半格计算。 (2)填表。 (3)它们的面积( )。 3.教材第88页情境图。 (1)把一个平行四边形沿( )剪开,通过割补平移转化成一个长方形。长方形的长相当于平行四边形的( ),长方形的宽相当于平行四边形的( ),拼出的长方形的面积与原来平行四边形的面积( )。 (2)比较发现:长方形的面积=( )×( ); 平行四边形的面积=( )×( )。 (3)如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成:( )。 4.教材第88页例1。 (1)花坛的形状是( ),要求花坛的面积,也就是求( )的面积。 (2)已知平行四边形的底和高,代入面积公式计算。 S=( )=( )×( )=( )(m2)
5.填表。 6.一个平行四边形的停车位,长是5 m,高是2.5 m,它的面积是多少
每日 口算 2.2÷2= 3.9÷3= 12.8÷4= 1.3×0.5= 1.7×0.2= 2.8÷0.4= 1.8×30= 169÷1000=
2 三角形的面积
预习指南:掌握三角形的面积计算公式,会计算三角形的面积。理解拼成的平行四边形和原来三角形的关系。
温故 知新 1.求下面平行四边形的面积。
2.教材第91页情境图。 (1)动手操作。 ①两个完全一样的( )三角形可以拼成一个( )形。 ②两个完全一样的( )三角形可以拼成一个( )形。 ③两个完全一样的( )三角形可以拼成一个( )形。 (2)观察发现。 把两个( )的三角形拼在一起,可以得到一个( )形,平行四边形的底等于三角形的( ),平行四边形的高等于三角形的( ),平行四边形的面积是其中一个三角形面积的( ),所以三角形的面积=平行四边形的面积÷( ),即三角形的面积=( )×( )÷( ),用字母表示为S=( )。 3.教材第92页例2。 (1)红领巾的形状是( ),要求它的面积,也就是求( )的面积。 (2)已知三角形的底和高,代入面积公式计算。 S=( )=( )×( )÷( )=( )(cm2)
4.求下面三角形的面积。
每日 口算 3.6÷1.8= 0.38+1.2= 0.36×20= 4-2.5= 17÷85= 2.8÷0.4= 0.27×3= 8×1.1=
3 梯形的面积
预习指南:掌握梯形的面积计算公式,能用梯形的面积公式解决实际问题。
温故 知新 1.写出梯形的各部分名称。
2.教材第95页情境图。 (1)拼摆法。 ①两个( )的梯形能拼成一个平行四边形。 ②梯形的( )等于平行四边形的( ),梯形的高等于平行四边形的( ),一个梯形的面积等于拼成的平行四边形面积的( )。 ③ (2)分割法。 ①将一个梯形分割成两个( )形。 梯形的面积=三角形①的面积+三角形②的面积 =( )×( )÷2+( )×( )÷2 =( + )×( )÷( ) ②将一个梯形分割成一个( )形和一个( )形。 梯形的面积=( )形面积+( )形面积 =( )+( ) =( + )×( )÷( ) (3)梯形的面积= ,如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式用字母表示为 。 3.教材第96页例3。 (1)我国三峡水电站大坝的横截面的一部分是( ),要求它的面积,也就是求( )的面积。 (2)已知梯形上底、下底和高,代入面积公式计算。 S=( )=( + )×( )÷( )=( )(m2)
4.计算下面梯形的面积。(单位:cm)
每日 口算 4.06×100= 16×0.2= 0.5÷0.2= 7÷0.5= 0.9÷4.5= 4.6×0.1= 0.35×2= 4.2÷2=
4 组合图形的面积
预习指南:计算组合图形的面积,关键是采用分割法、添补法等常用的方法,把组合图形转化成已学过的简单图形,再分别计算面积,最后相加、减。
温故 知新 1.用公式表示各图形的面积。 平行四边形的面积=( ); 三角形的面积=( ); 梯形的面积=( )。
2.教材第99页情境图。 (1)认识图形。 图中的图形分别是中队旗、房屋的一面墙、风筝和由七巧板拼成的一个( )形。 (2)观察发现。 中队旗由( )组合而成;小房子由( )组合而成;风筝由( )组合而成;七巧板拼成的长方形由( )组合而成。 (3)认识组合图形。 组合图形可以看成是由几个简单图形组合而成的。 3.教材第99页例4。 计算房子侧面墙的面积,可以将其看成是由几个简单图形组合而成的,再计算。 (1)可以把它看成是由一个( )形和一个( )形的组合的。 列式解答:
(2)可以把它分割成两个完全相同的( )形。 列式解答:
(3)求组合图形的面积时,可以把组合图形分割成若干个我们学过的图形,把各个图形的面积( );还可以把组合图形补成我们学过的简单图形,再减去补上的图形面积。
4.一面中国少年先锋队中队旗的面积是多少 (至少用两种方法) 5.一个指示牌的形状如下图,求它的面积。
每日 口算 1.2×20= 20.6-2.6= 6.5÷5= 40×0.4= 1.4×6= 12.5÷0.5= 1.3×0.7= 2.1÷0.03=
5 不规则图形的面积
预习指南:借助方格纸估算不规则图形的面积,并将不规则的图形转化成学过的图形进行估算。
温故 知新 1.数一数,算一算。
2.教材第100页例5。 (1)阅读与理解。 已知每个小方格的面积是1 cm2,要估计这片形状不规则的叶子的面积。 (2)分析与解答。 方法一:数方格。 在方格纸上描出叶子的轮廓图。图中的每个小方格表示( ),方格纸上满格的一共有( )格,不是满格的也有( )格,所以这片叶子的面积在( )cm2~( )cm2之间。如果把不满一格的都按半格计算,这片叶子的面积大约是( )cm2。 方法二:转化法。 将这片叶子的图形近似转化成平行四边形,底是( )cm,
高是( )cm,根据( )的面积计算公式,它的面积
大约是( )cm2。 (3)回顾与反思。 估算不规则图形的面积可以先通过( )确定面积的范围,再数一数满格的格数和不满格的格数;也可以( )为学过的图形来估算。
图中每个小方格的面积代表1 m2,
请你估计阴影部分的面积。
4.下面是一块近似三角形的荷塘,底是
56 m,高是30 m,这个荷塘的面积大约
是多少平方米
每日 口算 2.8×0.2= 14.8÷2= 4.5×0.6= 12.6÷3= 2.5×0.5= 12.3÷3= 8×0.09= 1.62÷2=
七 植 树 问 题
植 树 问 题
预习指南:运用画图策略理解并发现植树问题中间隔数和棵数的规律,解决生活中的实际问题。
温故 知新 1.一根木头平均截成6段,需要截几次
2.教材第106页例1。 (1)猜想。 在一条长100 m的小路一边植树,每隔5 m栽一棵,共栽100÷5=( )(棵)。 (2)验证。 ①20 m长的路,每隔5 m栽1棵(两端要栽),20 m里面有( )个5 m,要栽( )棵树。 ②25 m长的路,每隔5 m栽1棵(两端都栽),25 m里面有( )个5 m,要栽( )棵树。 …… ③在一条路的一边栽树,两端都栽时, 总长÷间距=( ),( )+( )=( )。 (3)解决问题:100÷5=20 20( )=( )(棵) 答:一共要栽 棵树。 3.教材第107页例2。 (1)画线段图理解间隔数与棵数的关系: 在一条线段上栽树,两端都不栽时,棵数=间隔数( )。 (2)解决问题:60÷3=20 20( )=( )(棵) ( )×2=( )(棵) 答:一共要栽 棵树。 4.教材第108页例3。 (1)假设周长是40 m,画图理解题意。 发现:圆形池塘可以看成封闭曲线,相当于只栽一端,间隔数棵数。 (2)解决问题:120÷10=( )(棵) 答:一共要栽 棵树。
5.有一条长160 m的路,工人们在路的一旁每隔2 m栽一棵树。如果两端都栽,则要栽( )棵;如果只栽一端,则要栽( )棵;如果两端都不栽,则要栽( )棵。 6.一根木头长10 m,要把它平均分成5段,每锯下一段需要8分钟,锯完一共需要多少分钟
每日 口算 2.5÷5= 4.5×0.1= 2.1÷0.7= 0.2×13= 0.4×5= 1.4÷0.7= 1.6÷0.2= 40.8÷8=
参考答案
一 小 数 乘 法
1 小数乘整数
1.35 3 105 60
2.3.5 3 3 3.5 加法 3.5 3.5 3.5 10.5 3.5 3 5 3.5 3 5 3 3 9 5 3 15 1 5 9 1 5 10 5 10.5 3.5 35 3.5 35 10.5 105 3.5 35 105 10.5
3. (1)100 100
(2)相同 整数 几 去掉
4.23 2 右 一
5.8.2 205 86.8 124
每日口算:1.2 1.5 3 8.4 1.4 8.6 7.7 0
2 小数乘小数(1)
1.4 7.7 9.2 0.1 3.8 6.6 3.6 9.9
2.2.4 0.8 0.9 面积 0.9
(1)1.92 10 10 100
(2)1.728 100 10 1000
(3)①小数点 ②因数 右边
(4)2.4×0.8=1.92(cm2)
1.92×0.9=1.728(kg)
答:一共需要1.728 kg油漆。
3.224 四 0.0224 0
4.两位 四位 三位
5.
每日口算:0.084 0.98 0.096 0.6 2.1 1
1.41 0.062
小数乘小数(2)
1.10 100 1 1 0.26 2 3 32
2.56千米/时 1.3 56 1.3 56×1.3
(1)①不对。 ②改正:
(2)
(3)56×1.3=72.8(千米/时)
答:鸵鸟的最高速度是72.8千米/时。
3.大 小
4.
每日口算:0.19 0.72 0.48 0.96 0.1 0.03 0.1 5.04
3 积的近似数
1.7 6.9 6.93 4 3.9 3.90 8 7.9 7.87
2.0.049 45 0.049 45 乘法 0.049×45
(1)四舍五入
(2)2.2 0 5
(3)积 下一位 四舍五入 约等 不能
(4)0.049×45≈2.2(亿个)
答:狗约有2.2亿个嗅觉细胞。
3.(1)0.72 百分 2 舍去 0.7
(2)0.765 千分 5 百分 进一 0.77
4.0.86×1.2≈1.03 2.34×0.15≈0.35
5.25×9.75≈244(元)
答:大约需要244元。
每日口算:1.05 0.085 1.3 1.41 0.54 0.294 0.1 0.9
4 整数乘法运算定律推广到小数
1. 25×95×4 25×32
=25×4×95 =25×4×8
=100×95 =100×8
=9500 =800
4×48+6×48 102×56
=(4+6)×48 =(100+2)×56
=10×48 =100×56+2×56
=480 =5600+112
=5712
2.a×b=b×a (a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
3.= = = 同样适用 简便
4.200 200+2 乘法分配
5. 4.8×0.25 1.5×105
=4×1.2×0.25 =1.5×(100+5)
=4×0.25×1.2 =1.5×100+1.5×5
=1.2 =157.5
45.2×99 1.2×2.5+0.8×2.5
=45.2×(100-1) =(1.2+0.8)×2.5
=45.2×100-45.2×1 =2×2.5
=4474.8 =5
2.33×0.5×4
=2.33×(0.5×4)
=2.33×2
=4.66
每日口算:84 0.108 0.96 0.642 0.6 1
10 1.5
5 解决问题(1)
1.7200 2000 1800 1000
2.(1)2 0.8 1 100
单价 数量 总价
大米 30.6元 2袋 —
肉 26.5元 0.8 kg —
鸡蛋 10元 1盒 —
20元 1盒
(2)62 99 60 20 100
(3)估大 估大 估小 估小
3. 2.8元<3元 3.9元<4元
4×3+6×4=36(元) 36元<50元
答:王阿姨付50元,够了。
4.12.3元>12元 18.6元>18元
4×12+2×18=84(元) 100-84=16(元)
16元<20元
答:剩下的钱不够买2个文具盒。
每日口算:1.62 1.2 0.7 0.8 2.7 0.072 0.1
0.096
解决问题(2)
1. 8+3.4×5 6.5-0.8×3.2
=8+17 =6.5-2.56
=25 =3.94
2.(1)7 1.5 7
(2)7 1.5 7+1.5×4=7+6=13(元)
(3)1.5 7 1.5×7=10.5(元)
7-1.5×3=2.5(元) 10.5+2.5=13(元)
3.7 8.5 10 11.5 13 14.5 16 17.5
4.5+(20-2)×1.2=26.6(元)
答:至少需要26.6元。
5.0.22+(8-3)×0.11=0.77(元)
答:她这一次通话的费用是0.77元。
每日口算:10 50 0.68 0.11 0.25 60 8.4
0.17
6 解 决 问 题
1.(1)四 0.55
(2)2.06 2.1
2.(1)2.5 2.5÷0.4
(2)6.25 2.4 0.1 7
(3)2.5÷0.4=6.25≈7(个)
答:需要准备7个瓶子。
3.(1)25 1.5 25÷1.5
(2)16.666… 25.5 0.5 16
(3)25÷1.5=16.666…≈16(个)
答:这些红丝带可以包装16个礼盒。
(4)进一 去尾
4.(1)5 (2)6 (3)7
5.38÷5≈8(辆)
答:需要准备8辆这样的小汽车。
每日口算:0.2 3 25.4 5 3 4 10 30
二 位 置
位 置
1.3 2(答案不唯一) 列 行
2.(1)左 右 前 后 列数 行数 逗号
(2)(2,3)
(3)(3,4)(4,3) 6 4
3.(1)3 0
(2)(3,5) (1,4) (2,2) (6,4) (3)略。
(4)列数 行数
4.(3,4) 5 2
5.(1)A(1,1) B(4,1) C(2,3)
(2)画图略。 A'(5,4) B'(8,4) C'(6,6)
每日口算:0.078 0.072 10.8 75 20.4 2050
2.22 0.206
三 小 数 除 法
1 除数是整数的小数除法
1.
2.(1)除 22.4÷4
(2)22400 22400 4 5600 5600 5.6
被除数 十分之一
(3)22.4÷4=5.6(km)
答:他平均每周应该跑5.6 km。
3.(1)除 28÷16
(2)十 百 整数 商 被除数 0 0
(3)28÷16=1.75(km)
答:平均每天慢跑1.75 km。
4.(1)除 5.6÷7
(2)0 5 6 0 相同 商 除数
(3)5.6÷7=0.8(km)
答:平均每天要跑0.8 km。
5. 7.83÷9=0.87 43.5÷29=1.5
14.21÷7=2.03 1.35÷15=0.09
6.(1)2.4÷2=1.2(元)
答:每块橡皮1.2元。
(2)4.8÷2=2.4
答:一套尺子的价钱是一个圆规价钱的2.4倍。
每日口算:0.6 0.6 1.4 3.4 0.3 0.3 0.3
1.7
2 一个数除以小数
1.2009 6 扩大 1000
2.133 37.2
3.(1)7.65 0.85 除 7.65÷0.85 (2)765 85 9 100 85 100 765 765 85 9
(3)7.65÷0.85=9(个)
答:这些丝绳可以编9个“中国结”。
4.45 0
(1)100 28 100 商不变 0 两
(2)①除数 整数 ②除数 被除数 0
③整数
5.
每日口算:2 9 1.3 12 0.8 8 1.1 0.5
3 商的近似数
1.1 1.0 0.99 4 4.5 4.50 3 3.1 3.09
2.(1)总价 数量 除法 19.4÷12
(2)
①1.62 三 分 ②1.6 二 角
(3)一 四舍五入 不能
(4)19.4÷12≈1.62(元)
答:每个大约1.62元。
或19.4÷12≈1.6(元)
答:每个大约1.6元。
3.
每日口算:2 30 200 2.5 2.3 0.6 0.4 1.3
4 循 环 小 数
1.4÷7≈0.57 16÷3≈5.33 2÷9≈0.22
2.(1)路程 时间 除 400÷75
(2)
25 3
(3)400÷75=5.333…(米)
答:平均每秒跑5.333…米。
3.(1)10 5
(2)5 6 4 5
(3)重复 循环 重复 循环节
(4)5. 0.0
(5)有限 无限
4.7.234 5.051 3.646
5.> < >
每日口算:0.7 0.6 0.6 0.9 0.06 0.4 100
1.1
5 用计算器探索规律
1.(1)2.0
(2)0.25 0.16
2.(1)0.2727… 0.3636… 0.4545…
(2)09 18 0.2727… 27
0.3636… 36 0.4545… 45 9
(3)0.5454… 0.6363… 0.7272… 0.8181…
(4)计算 规律 规律 结果 算式
3.(1)3.333 3.3333 3.33333
(2)0. 0. 0.
(3)1111.2222 11111.22222 111111.222222
4.0.444… 0.555… 0.777…
5.444.222 4444.2222
每日口算:0.046 30 50 8 300 30 300 30
四 可 能 性
可 能 性
1.可能 可能
2.(1)唱歌 跳舞 朗诵 3
(2)唱歌 朗诵 2
(3)一定
(4)确定 确定 一定 不可能 不确定 不确定
可能
3.(1)两 红 蓝 两
(2)14 6
(3)17 3
(4)红 蓝 大 小
4.(1)两 红 黄 两
(2)红 黄 红 黄 红 黄 数量 多 少
5.两 红 3 黄 不可能
每日口算:7 2 1.2 0.4 2.1 4 50 0.8
五 简 易 方 程
1 用字母表示数(1)
1. 中国中央电视台 1 13 11 12
2.(1)2+30=32 3+30=33
(2)小红 30 a+30 (3)41
3.(1)2×6=12 3×6=18
(2)地球 6 x×6 前
(3)90
4.(1)178-a
(2)20b
5. 4x 48
6. (1)a+b+c (2)2b+a
每日口算:6 3 0.07 20 7.24 2 1.2 0.4
用字母表示数(2)
1. 4b 5x am 3c y2
2.(1)vt
(2)80×30=2400(m)
答:30分钟能走2400米。
3.(1)a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a a·b=b·a或ab=ba
(a×b)×c=a×(b×c) (a·b)·c=a·(b·c)或(ab)c=a(bc)
(a+b)×c=a×c+b×c
(a+b)·c=a·c+b·c或(a+b)c=ac+bc 省略
(2)①C=4a S=a2 a的平方 2 a 乘
②4a 4 6 24 a2 6 6 36
4. 37 63 a b 6 b a b 2.4 9 5
5.C=(a+b)×2=(8+3)×2=22(cm)
S=ab=8×3=24(cm2)
每日口算:16 0.02 0.55 5 0.05 4 20 0.7
用字母表示数(3)
1.连线略。a2=a×a 4.5×4.5=4.52 x+x=2x b×1=b
2.(1)- 3小杯果汁的质量
(2)3x 1200 1200-3x
(3)600 0 1200 400
3.(1)3 3x 4 4x 7 7x 3x+4x (2)7x
(3)56
4.(1)5x-8
(2)5x-8=5×25-8=117
答:柳树有117棵。
5.(1)11x
(2)11x=11×15=165
答:一共用了165根小棒。
每日口算:0.07 0.72 5.3 0.93 1.8 2 19.2 2
2 方程的意义和等式的性质(1)
1.12y 10x 0.65b 18a
2.(1)50 50 100 等式
(2)①100 ②100+x 100+x>100
100+x>200 100+x<300 100+x=250
3.(1)3x 3x=2.4
(2)未知数 等式 方程 等式 未知数
(3)略。
4. x+3.6=7 8-x=2 2x+3y=9
5. 4x=16.8 x+129=288
每日口算:0.11 5 0.09 3 0.53 0.084 2.3 0.2
方程的意义和等式的性质(2)
1.(1) (2) (3)
2.(1)a=2b 平衡 a+b=2b+b
(2)a+b=4b 平衡 a+b-b=4b-b 1 3
(3)加上 减去 相等
3.(1)a=b 平衡 2a=2b
(2)2a=6b 平衡 2a÷2=6b÷2
(3)0 相等
4.6 8 2 3 c c
每日口算:0.12 2 9 3 40 0.64 72 0.427
3 解方程(1)
1.a 8 3.5 c
2.(1)x+3=9
(2)3
(3)3 3 等式的性质1 6
(4)未知数 解 解方程 值 过程
(5)6 9 左 相等 x=6
3.3 3 等式的性质2 6
4.x x 等式的性质1 9 9 等式的性质1 11
5. x+3.2=4.6
解:x+3.2-3.2=4.6-3.2
x=1.4 5x=6
解:5x÷5=6÷5
x=1.2
18-x=3
解:18-x+x=3+x
3+x-3=18-3
x=15
每日口算:4 5 0 16.8 0.8 0.03 2 0.02
解方程(2)
1. 2.4x=6
解:2.4x÷2.4=6÷2.4
x=2.5 x-1.8=4
解:x-1.8+1.8=4+1.8
x=5.8
5.7÷x=3
解:5.7÷x×x=3×x
3x÷3=5.7÷3
x=1.9
2.(1)4 40 3x+4=40
(2)4 36 4 4 等式的性质1 3 3 等式的性质2 12
3×12+4 40 方程右边 12
3.2 2 x-16 16 16 20 乘法分配 32 32
2 2 20
4. (1) 2x+48=102
解:2x+48-48=102-48
2x÷2=54÷2
x=27 (2)2(x+25)=76
解:2(x+25)÷2 =76÷2
x+25-25=38-25
x=13
每日口算:20 63.9 0.05 0.84 2 2 8 0.6
4 实际问题与方程(一)
1. x+19=51
解:x+19-19=51-19
x=32 2x=16.2
解:2x÷2=16.2÷2
x=8.1
9x+36=72
解:9x+36-36=72-36
9x÷9=36÷9
x=4
2.(2)原纪录 超出部分 小明的成绩
(3)4.15 不写 (4)4.15 4.21 x=4.15
3.(1)黑 白
(2)2x 12 12
(3)①未知数 x ②数量 等量 方程
③解方程 检验
4.解:设一共装了x筒。
5x+3=1428
x=285
答:一共装了285筒。
每日口算:44 0.88 1.08 8 5 2 200 2.02
5 实际问题与方程(二)
1. 3x+4×2.5=46
解:3x+10-10=46-10
3x÷3=36÷3
x=12
x+2.5x=17.5
解: 3.5x=17.5
3.5x÷3.5=17.5÷3.5
x=5 9x+11x=100
解:20x=100
x=5
2.(1)苹果 梨
2x+5.6=10.4
2x+5.6-5.6=10.4-5.6
2x÷2=4.8÷2
x=2.4
答:苹果每千克2.4元。
(2) (2.8+x)×2÷2=10.4÷2
2.8+x=5.2
2.8+x-2.8=5.2-2.8
x=2.4
答:苹果每千克2.4元。
3.(1)陆地 海洋
(2)陆地 海洋 乘法分配 1.5 1.5 3.6 1.5 3.6 1.5 3.6
4.(1)解:设下午要运x次才能运完。
5(3+x)=35
x=4
答:下午要运4次才能运完。
(2)解:设小明今年x岁,则妈妈今年3x岁。
3x-x=24
x=12
3x=36
答:小明今年12岁,妈妈今年36岁。
每日口算:56 10 90 3.2 0.4 0.8 42 0.72
6 实际问题与方程(三)
1. 5(x+1.5)=17.5
解:5(x+1.5)÷5=17.5÷5
x+1.5-1.5=3.5-1.5
x=2
8(x-6.2)=41.6
解:8(x-6.2)÷8=41.6÷8
x-6.2+6.2=5.2+6.2
x=11.4
6x+35×6=360
解:6x+210-210=360-210
6x÷6=150÷6
x=25
2.(1)250 200 4.5
(2)小林 小云
两人x分钟后相遇
乘法分配 0.45 0.45 10 9:10
(3)线段图 路程 速度和
3.(1)解:设x天后能够铺完这条公路。
80x+60x=1400
x=10
答: 10天后能够铺完这条公路。
(2)解:设乙车的速度是x千米/时。
2.4x+42×2.4=216
x=48
答: 乙车的速度是48千米/时。
每日口算:60 0.3 0.042 6 18 110 90 30
六 多边形的面积
1 平行四边形的面积
1.画法不唯一。
2.面积 长方 长 宽 平行四边
(2)6 m 4 m 24 m2 6 m 4 m 24 m2
(3)相等
3.(1)高 底 高 相等
(2)长 宽 底 高
(3)S=ah
4.(1)平行四边形 平行四边形
(2)ah 6 4 24
5.(竖排)798 21.5 5.2
6.5×2.5=12.5(m2)
答:它的面积是12.5 m2。
每日口算:1.1 1.3 3.2 0.65 0.34 7 54 0.169
2 三角形的面积
1.24×40=960(cm2)
2.(1)①锐角 平行四边 ②钝角 平行四边
③直角 平行四边
(2)完全相同 平行四边 底 高 2倍 2 底 高 2 ah÷2
3.(1)三角形 三角形
(2)ah÷2 100 33 2 1650
4.8×9.2÷2=36.8(cm2) 14×15÷2=105(cm2)
10×18÷2=90(dm2)
每日口算:2 1.58 7.2 1.5 0.2 7 0.81 8.8
3 梯形的面积
1.上底 下底 腰 高
2.(1)①完全相同 ②上底加下底 底 高 一半
(2)①三角 上底 高 下底 高 上底 下底 高
2 ②平行四边 三角 平行四边 三角 上底×高
(下底-上底)×高÷2 上底 下底 高 2
(3)(上底+下底)×高 ÷2 S=(a+b)×h÷2
3.(1)梯形 梯形
(3)(a+b)×h÷2 36 120 135 2 10530
4. (12+18)×9÷2
=30×9÷2
=135(cm2)
(7.2-1.6-2.2+7.2)×4.8÷2
=10.6×4.8÷2
=25.44(cm2)
每日口算:406 3.2 2.5 14 0.2 0.46 0.7 2.1
4 组合图形的面积
1.底×高 底×高÷2 (上底+下底)×高÷2
2.(1)长方 (2)2个梯形 三角形和正方形 4个三角形 5个三角形、1个正方形和1个平行四边形
3.(1)正方 三角 5×5+5×2÷2=30(cm2)
(2)梯 (5+5+2)×2.5÷2×2=30(cm2)
(3)相加
4.第一种方法:
30×2×80-30×2×20÷2=4200(cm2)
第二种方法:
(80+80-20)×30÷2×2=4200(cm2)
答:一面中国少年先锋队中队旗的面积是4200 cm2。
5. 20×10+10×20÷2=300(cm2)
答:它的面积为300 cm2。
每日口算:24 18 1.3 16 8.4 25 0.91 70
5 不规则图形的面积
1.3 2 6 2 4 8
2.(2)1 cm2 18 18 18 36 27 5 6 平行四边形 30
(3)数方格 转化
3.答案不唯一。30 m2
4.56×30÷2=840(m2)
答:这个荷塘的面积大约是840平方米。
每日口算:0.56 7.4 2.7 4.2 1.25 4.1 0.72
0.81
七 植 树 问 题
植 树 问 题
1.5次
2.(1)20 (2)①4 5 ②5 6
③间隔数 间隔数 1 棵数
(3)+ 1 21 21
3.(1)- 1
(2)- 1 19 19 38 38
4.(1)=
(2)12 12
5.81 80 79
6.(5-1)×8=32(分)
答:锯完一共需要32分钟。
每日口算:0.5 0.45 3 2.6 2 2 8 5.1
一 小 数 乘 法
1 小数乘整数
预习指南:掌握小数乘整数的计算方法。利用已学过的“元、角、分”等单位间的换算,将高级单位转化成低级单位,从而使小数乘法转化成整数乘法进行计算。
温故 知新 1.填一填。 35+35+35=( )×( )=( ) 12×5=( )
2.教材第2页例1。 已知每个( )元,求买( )个多少钱,也就是求( )个( )元是多少。 方法一:用( )计算。 ( )+( )+( )=( )(元) 方法二:将( )元化成( )元( )角进行计算。 ( )元=( )元( )角 ( )元×( )=( )元 ( )角×( )=( )角=( )元( )角 ( )元+( )元( )角=( )元( )角=( )元 方法三:将“( )元×3”转化为“( )角×3”进行计算。 3.教材第3页例2。 (1) (2)小数乘整数的意义与整数乘法的意义( ),在计算小数乘整数时,可以将小数乘法转化成( )乘法进行计算,因数中有几位小数,积中也应该有( )位小数。若积的小数部分末尾有0,要根据小数的基本性质把积中小数末尾的0( )。
4.计算2.3×2时,可以把它当成( )×( )进行计算,算出积后,再从积的( )边起,数出( )位点上小数点。 5.列竖式计算。
每日 口算 0.3×4= 3×0.5= 5×0.6= 2.1×4= 0.7×2= 2×4.3= 7×1.1= 5.7×0=
2 小数乘小数(1)
预习指南:掌握小数乘小数的计算方法。知道积的小数位数不够时,要在前面用0补足。
温故 知新 1.直接写出得数。 0.5×8= 1.1×7= 2.3×4= 0.01×10= 1.9×2= 2×3.3= 2×1.8= 3.3×3=
2.教材第5页例3。 已知宣传栏是长为( )m,宽为( )m的长方形,每平方米要用油漆( )kg。要求一共需要多少千克油漆,需先算出长方形宣传栏的( ),再乘( )得到一共需要的油漆的质量。 (1)先求长方形宣传栏的面积。
2.4×0.8= (cm2)
(2)再算需要多少千克油漆。
1.92×0.9= (kg)
(3)小数乘法的计算步骤。 ①先按照整数乘法算出积,再点( ); ②点小数点时,看( )中一共有几位小数,就从积的( )起数出几位,点上小数点。 (4)规范解答: 3.教材第6页例4。 乘得的积的小数位数不够时,要在前面用( )补足,再点小数点。
4.判断下面各个积的小数位数。 3.72×28( ) 3.72×0.28( ) 372×0.028( ) 5.列竖式计算。 1.8×2.3= 0.37×0.4= 1.06×25=
每日 口算 0.42×0.2= 1.4×0.7= 0.16×0.6= 1.2×0.5= 0.6×3.5= 0.8×1.25= 0.3×4.7= 3.1×0.02=
小数乘小数(2)
预习指南:正确解决倍数是小数的实际问题,根据数据的特点灵活选择验算方法。
温故 知新 1.直接写出得数。 12.5×0.8= 12.5×8= 0.25×4= 0.04×25= 0.13×2= 8×0.25= 0.06×50= 0.04×800=
2.教材第7页例5。 已知非洲野狗的最高速度是( ),鸵鸟的最高速度是非洲野狗的( )倍。要求鸵鸟的最高速度是多少千米/时,就是求( )的( )倍是多少,列式为 。 (1)竖式展示。 ①56×1.3=7.28 ②如果不对,请在下面改正。 (2)验算方法。 方法一:交换两个因数的位置重新计算。 方法二:因数与积的大小关系。 1.3>1,所以56×1.3的积应该比56大,由此得出计算结果错误。 方法三:用计算器验算。 (3)规范解答:
3.一个数(0除外)乘大于1的数,积比原来的数( )。 一个数(0除外)乘小于1的数,积比原来的数( )。 4.列竖式计算并验算。 42×3.7= 8.4×0.45= 3.5×0.6=
每日 口算 0.38×0.5= 0.6×1.2= 0.4×1.2= 3.2×0.3= 0.2×0.5= 0.05×0.6= 0.25×0.4= 504×0.01=
3 积的近似数
预习指南:学会用“四舍五入”法取积的近似数。先算出准确数,再根据需要保留一定的小数位数;在求积的近似数时,小数末尾的0不能去掉,否则精确度就变了。
温故 知新 1.填表。 保留整数保留一位小数保留两位小数6.9343.9047.8685
2.教材第11页例6。 已知人的嗅觉细胞约有( )亿个,狗的嗅觉细胞个数是人的( )倍。求狗约有多少亿个嗅觉细胞,就是求( )的( )倍是多少,用( )计算,列式为 。 (1)要求得数保留一位小数,就是用( )法取积的近似数。 (2)列竖式计算。
(3)求积的近似数时,先确定( )的小数位数,再看需要保留数位的( ),用( )的方法取舍。近似数与准确数有区别,近似数应该用( )号连接。取积的近似数时,小数末尾的0( )(填“能”或“不能”)去掉。 (4)规范解答:
3.填空题。 (1)0.8×0.9的积是( ),得数保留一位小数,要看( )位上的( ),应( ),结果是( )。 (2)1.7×0.45的积是( ),精确到百分位,就要看( )位上的( ),应向( )位( )。结果是( )。 4.列竖式计算。(得数保留两位小数) 0.86×1.2≈ 2.34×0.15≈ 5.刘老师买25本《童话故事》,大约需要多少钱
每日 口算 10.5×0.1= 0.5×0.17= 6.5×0.2= 0.3×4.7= 1.8×0.3= 0.42×0.7= 0.25×0.4= 2×0.45=
4 整数乘法运算定律推广到小数
预习指南:掌握小数四则混合运算的运算顺序,理解整数乘法运算定律对于小数乘法同样适用,并能运用乘法运算定律进行简便计算。
温故 知新 1.计算。 25×95×4 25×32 4×48+6×48 102×56 2.用字母表示下列整数乘法运算定律。 乘法交换律: 乘法结合律: 乘法分配律:
3.教材第12页小天使。 观察下面每组中的两个算式,它们有什么关系 0.7×1.2○1.2×0.7 (0.8×0.5)×0.4○0.8×(0.5×0.4) (2.4+3.6)×0.5○2.4×0.5+3.6×0.5 通过观察、计算发现:整数乘法的运算定律在小数乘法中( ),运用这些定律可以使一些计算( )。 4.0.65×202,202接近( ),把这个数拆成( )的形式,再运用( )律简算。
5.用简便方法计算下面各题。 4.8×0.25 1.5×105 45.2×99 1.2×2.5+0.8×2.5 2.33×0.5×4
每日 口算 4.2×20= 1.2×0.09= 1.2×0.8= 1.07×0.6= 1.5×0.4= 0.2×5= 0.8×12.5= 0.2×5+0.5=
5 解决问题(1)
预习指南:能运用估算的知识解决实际问题。会用表格的形式整理信息,能根据实际问题和具体数据选择适当的估算策略。
温故 知新 1.估算。 76×89≈ 38×51≈ 102×18≈ 53×21≈
2.教材第15页例8。 (1)阅读与理解。 妈妈买了( )袋大米和( )kg肉,还想买( )盒鸡蛋。要想知道剩下的钱够不够,只要把买到的所有商品的价格加在一起,与( )元进行比较,可以用估算的方法解决。用表格表示妈妈买的东西,如下: 单价数量总价大米—肉—鸡蛋—
(2)分析与解答。 小亮:1袋大米不到31元,2袋不到( )元;肉不到27元;买一盒10元的鸡蛋,总共不超过( )元,够了。 小丁:1袋大米超过30元,2袋超过( )元;1 kg肉超过25元,0.8 kg也就超过( )元;再买一盒20元的鸡蛋,总共就超过了( )元,不够。 (3)回顾与反思。 小亮和小丁的方法有什么不同 小亮是通过把物品的钱数( ),发现( )后的总钱数不超过100元,判断出“够买”。 小丁是通过把物品的钱数( ),发现( )后的总钱数等于100元,所以总钱数超过了100元,判断出“不够买”。
3.王阿姨买4 kg香蕉和6 kg苹果,已知香蕉每千克2.8元,苹果每千克3.9元。王阿姨付50元,够吗 4.小明带100元去超市购物,他买了4本《故事书》和2盒彩笔,剩下的钱还够买2个文具盒吗
每日 口算 0.2×8.1= 0.8×1.5= 3.5×0.2= 1.6×0.5= 4.5×0.6= 3.6×0.02= 0.25×0.4= 4.8×0.02=
解决问题(2)
预习指南:有条理地整理题中有用的信息,能准确地找到分段计费问题的数量关系,运用分段计算的方法正确解答这类实际问题。
温故 知新 1.计算。 8+3.4×5 6.5-0.8×3.2
2.教材第16页例9。 (1)阅读与理解。 已知出租车的收费标准是3 km以内( )元;超过3 km的部分,每千米( )元(不足1 km按1 km计算)。行驶6.3 km,要按( )km计算付多少钱。 (2)分析与解答。 方法一:分段计算法。
前面3 km应收( )元,后面4 km按每千米( )元计算。
列式为 方法二:假设调整法。
先按每千米( )元算出( )km需要的钱数,再加上前3 km少算的钱数。
列式为 (3)回顾与反思。 制作10 km以内出租车价格表,对照价格表检验计算结果是否正确。 行驶的里程/km12345678910出租车费/元
4. 5.某地拨打市内电话前3分钟内0.22元,超过3分钟,每分钟收费0.11元(不足1分钟按1分钟算)。妈妈一次市内通话的时间是7分36秒,她这一次通话的费用是多少
每日 口算 0.2×50= 12.5×4= 0.4×1.7= 1.1×0.1= 0.5×0.5= 100×0.6= 2.8×3= 0.85×0.2=
6 解 决 问 题
预习指南:会用“进一法”和“去尾法”取商的近似数。在解决问题的过程中能根据具体问题确定取商的近似数的方法。
温故 知新 1.填空。 (1)3.25×0.17的积是( )位小数,保留两位小数是( )。 (2)1.85÷0.9的商保留两位小数约是( ),精确到十分位约是( )。
2.教材第39页例10(1)。 (1)阅读与理解。 已知分装2.5 kg香油,每个瓶子最多可盛0.4 kg。求需要准备几个瓶子,就是求( )里面有几个0.4,用除法计算,列式为 。 (2)分析与解答。 2.5÷0.4的计算结果是( ),瓶子不能有0.25个,应该取整数,用“四舍五入”法取近似数是6,但是6个瓶子只能装( )kg,还剩下( )kg,因此需要准备( )个瓶子。 (3)规范解答: 3.教材第39页例10(2)。 (1)阅读与理解。 已知每个礼盒要用1.5 m长的丝带,求25 m长的红丝带可以包装多少个礼盒,就是看( )里面有多少个( ),用除法计算,列式为 。 (2)分析与解答。 25÷1.5的计算结果是( )。盒子数不能是0.666…个,用“四舍五入”法取近似数是17,但是包装17个礼盒需要( )m长的红丝带,还差( )m,所以最多只能包装( )个礼盒。 (3)规范解答: (4)回顾与反思。 一般用“四舍五入”法取商的近似数,但是在解决实际问题时,要根据实际需要,用( )法或( )法取商的近似数。
4.结合生活实际,求出下面各题的近似数,并填在括号里。 (1)一块布料可以做5.8件同样的衣服,实际只能做( )件。 (2)一堆水泥,一辆汽车需要5.4次运完,实际需要运( )次。 (3)亮亮的零花钱可以买7.9支钢笔,实际可以买( )支钢笔。 5.一辆小汽车可以坐5人,五(2)班一共有38名学生准备去春游,需要准备多少辆这样的小汽车
每日 口算 2.8÷14= 8.1÷2.7= 50.8÷2= 4÷0.8= 5×0.6= 1.2÷0.3= 4÷0.4= 93÷3.1=
二 位 置
位 置
预习指南:明确行和列的意义,掌握用数对表示物体位置的方法。
温故 知新 1.教室里,你的座位在第( )排第( )列(根据自己班的情况填写)。通常我们把竖排叫做( ),横排叫做( )。
2.教材第19页例1。 (1)确定第几列,一般是从( )往( )数;确定第几行,一般是从( )往( )数。用数对表示位置时, ( )在前,( )在后,中间用( )隔开,最后用括号括起来。 (2)张亮在第2列、第3行的位置,可以用数对( , )表示。 (3)王艳同学的位置用数对表示是( , ),赵雪同学的位置用数对表示是( , ),看一看有什么不同。 (4)王乐同学的位置用数对表示是(6,4)是在第( )列、第( )行,在图上指出哪个是王乐同学。 3.教材20页例2。 (1)用数对(3,0)表示大门的位置,说明大门所在的位置对应的列数是( ),行数是( )。 (2)熊猫馆的位置是( , ),大象馆的位置是( , ),猴山的位置是( , ),海洋馆的位置是( , )。 (3)请在右图中标出下面场馆的位置。 飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3) (4)确定物体的位置时,先找到( ),再找到( ),最后描点标明。
4.小军坐在教室的第3列第4行,用数对表示为( , ),用数对(5,2)表示的某同学坐在第( )列第( )行的位置。 5.(1)用数对写出三角形各个顶点的位置。 A( , ) B( , ) C( , ) (2)将三角形向右平移4格,再向上平移3格后得到新图形三角形A'B'C'。画出新的三角形,并用数对表示新的三角形的三个顶点的位置。 A': ,B': ,C': 。
每日 口算 2.6×0.03= 1.8×0.04= 0.9×12= 30×2.5= 5.1×4= 41×50= 1.11×2= 1.03×0.2=
三 小 数 除 法
1 除数是整数的小数除法
预习指南:掌握除数是整数的小数除法的计算方法。理解商的小数点和被除数的小数点对齐的道理。
温故 知新 1.列竖式计算。 2145÷15= 416÷32= 1380÷15=
2.教材第24页例1。 (1)已知王鹏计划4周跑步22.4 km,求王鹏平均每周应跑多少千米,用( )法计算,列式为 。 (2)计算方法。 方法一:利用单位改写计算。 22.4 km=( )m ( )÷( )=( )m ( )m=( )km 方法二:列竖式计算。 (3)规范解答: 3.教材第25页例2。 (1)已知王鹏的爷爷计划16天慢跑28 km,求平均每天慢跑多少千米,用( )法计算,列式为 。 (2)列竖式计算。 除数是整数的小数除法,先按照( )除法的方法计算,( )的小数点要和( )的小数点对齐。哪一位不够商1,就在那一位上写( )占位。如果除到被除数的末尾仍有余数,要添上( )继续除。 (3)规范解答: 4.教材第25页例3。 (1)已知王鹏每周计划跑5.6 km,求平均每天要跑多少千米,用( )法计算,列式为 。
(2)列竖式计算。 (3)规范解答:
5.列竖式计算。 7.83÷9= 43.5÷29= 14.21÷7= 1.35÷15= 6.文具商店。 (1)玲玲买了2块橡皮,一共花了2.4元。你能求出每块橡皮多少钱吗 (2)一套尺子的价钱是一个圆规价钱的多少倍
每日 口算 2.4÷4= 4.2÷7= 8.4÷6= 6.8÷2= 3.9÷13= 3.6÷12= 8.1÷27= 6.8÷4=
2 一个数除以小数
预习指南:理解将“一个数除以小数”转化成“一个数除以整数”的算理。知道如果除数是小数,要先把除数变成整数,被除数的小数点移动位数与除数的相同。
温故 知新 1.把20.09扩大到它的100倍是( );0.006去掉小数点后是( ),结果( )到原来的( )。 2.在括号里填上适当的数。 13.3÷0.4=( )÷4 3.72÷1.2=( )÷12
3.教材第28页例4。 (1)已知编一个“中国结”要用0.85 m丝绳,求这些丝绳可以编几个“中国结”,就是求( )里面有几个( ),用( )法计算,列式为 。 (2)计算方法。 方法一:单位转化法,把“米”转化成“厘米”计算。 7.65 m=( )cm 0.85 m=( )cm 因为765÷85=9,所以7.65÷0.85=( )。 方法二:列竖式计算。 把0.85扩大到它的( )倍,是( ),为了使商不变,7.65也扩大到它的( )倍,变成( ),因此就把7.65÷0.85转化成了( )÷( ),商是( )。 (3)规范解答: 4.教材第29页例5。 12.6÷0.28= (1)把0.28扩大到它的( )倍,是( ),为了使商不变,12.6也扩大到它的( )倍,因为12.6是一位小数,根据( )的性质,在它的末尾用( )补足,再把小数点向右移动( )位。 (2)计算一个数除以小数时, ①先移动( )的小数点,使它变成( ); ②( )的小数点向右移动几位,( )的小数点也向右移动几位(位数不够的,在被除数的末尾用 补足); ③然后按除数是( )的小数除法进行计算。
5.列竖式计算。 5.98÷0.23= 197.6÷5.2= 10.8÷4.5=
每日 口算 1.6÷0.8= 7.2÷0.8= 7.8÷6= 0.48÷0.04= 6.4÷8= 2.4÷0.3= 0.88÷0.8= 4.5÷9=
3 商的近似数
预习指南:学会用“四舍五入”法求商的近似数。求近似数时,先看保留几位小数,就除到比需要的小数位数多一位,再用“四舍五入”法取近似数。
温故 知新 1. 用“四舍五入”法求下面各小数的近似数。 保留整数保留一位小数保留两位小数0.98814.49893.0924
2.教材第32页例6。 (1)已知12个羽毛球19.4元,求每个羽毛球大约多少钱。根据“单价=( )÷( )”可知,用( )计算,列式为 。 (2)列竖式计算。 ①保留两位小数:19.4÷12≈( )(元),要看小数部分第( )位上的数。计算价钱,保留两位小数,表示精确到( )。 ②保留一位小数:19.4÷12≈( )(元),要看小数部分第( )位上的数。计算价钱,保留一位小数,表示精确到( )。 (3)在计算小数除法需要求商的近似数时,一般除到比需要保留的小数位数多( )位,再按照( )法取商的近似数。保留小数位数,需要连续进位时,近似数末尾的0( )(填“能”或“不能”)去掉。 (4)规范解答:
3.列竖式计算,按要求取商的近似数。 48÷2.3≈ 1.55÷3.8≈ 3.81÷7≈ (保留一位小数) (保留两位小数) (精确到百分位)
每日 口算 0.9÷0.45= 3.9÷0.13= 80÷0.4= 50÷20= 6.9÷3= 3.6÷6= 3.2÷8= 9.1÷7=
4 循 环 小 数
预习指南:认识循环小数,能正确运用循环小数表示商。能用简便记法表示循环小数,知道循环小数一定是无限小数,无限小数不一定是循环小数。
温故 知新 1.列竖式计算。(结果保留两位小数) 4÷7≈ 16÷3≈ 2÷9≈
2.教材第33页例7。 (1)已知跑400 m用了75秒,求平均每秒跑多少米。根据“速度=( )÷( )”可知,用( )法计算,列式为 。 (2)列竖式计算。 列竖式计算时,每次除得的余数都是“( )”,商的小数部分总是重复出现“( )”。 (3)规范解答: 3.教材第33页例8。 (1)用竖式计算28÷18时,每次除得的余数都是“( )”,商的小数部分总是重复出现“( )”。 (2)用竖式计算78.6÷11时,除得的余数“( )”和“( )”重复出现,商的小数部分中“( )”和“( )”重复出现。 (3)一个数的小数部分,从某一位起,一个数字或者几个数字依次不断( )出现,这样的小数叫做( )小数。依次不断( )出现的数字,就是这个循环小数的( )。 (4)循环的数字只有一个的循环小数,可以只写一个循环的数字,并在这个数字的上面记一个圆点。例如:5.333…写作( );循环的数字是多个的循环小数,可以只写第一组循环的数字,并在这组数字的首位和末位的数字上面各记一个圆点。例如:0.203203…写作( )。 (5)小数部分的位数有限的小数叫( )小数,小数部分的位数无限的小数叫( )小数。
4.把下面的小数保留三位小数。 7.3≈ 5.≈ 3.6464≈ 5.在○里填上“>”“<”或“=”。 0.○0.444 2.○2.1 1.0○1.
每日 口算 3.5÷5= 4.2÷7= 9.6÷16= 4.5÷5= 1.8÷30= 0.28÷0.7= 90÷0.9= 0.88÷0.8=
5 用计算器探索规律
预习指南:能根据计算器计算的结果发现规律,并利用规律解决有关问题。
温故 知新 1.按规律填数。 (1)1,1.1,1.3,1.6,( )。 (2)0.81,0.64,0.49,0.36,( ),( )。
2.教材第35页例9。 (1)先计算出3÷11,4÷11,5÷11的得数。 3÷11=( ) 4÷11=( ) 5÷11=( ) (2)比较发现规律。 1÷11=0.0909…,商的循环节是( )。 2÷11=0.1818…,商的循环节是( )。 3÷11=( ),商的循环节是( )。 4÷11=( ),商的循环节是( )。 5÷11=( ),商的循环节是( )。 发现商的规律: 都是循环小数; 整数部分都是0; 循环节都是被除数的( )倍。 (3)根据发现的规律直接写出下面各题的商。 6÷11=( ) 7÷11=( ) 8÷11=( ) 9÷11=( ) (4)用计算器探索规律的方法:用计算器( )→观察发现( )→根据( )写结果。在寻找规律时,不仅要观察( ),还要观察( ),对比各自的特点,找到它们内在的联系,从而总结出规律。
3.根据规律填数。 (1)3,3.3,3.33, , , 。 (2)0.,0.,0., , , 。 (3)1.2,11.22,111.222, , , 。 4.运用规律直接写出下面三题的得数。 1÷9=0.111… 2÷9=0.222… 3÷9=0.333… 4÷9= 5÷9= 7÷9= 5.不计算,运用规律直接填出得数。 6×7=42 6.6×6.7=44.22 6.66×66.7=( ) 6.666×666.7=( )
每日 口算 0.23×0.2= 4.8÷0.16= 10÷0.2= 2.4÷0.3= 36÷0.12= 45÷1.5= 75÷0.25= 93÷3.1=
四 可 能 性
可 能 性
预习指南:感受随机事件发生的确定性和不确定性。能准确判断事件发生的可能性的大小。
温故 知新 1.任意抛一枚硬币,落地后,( )正面朝上,也( )反面朝上。(填“可能”或“不可能”)
2.教材第44页例1。 三张卡片上分别写着唱歌、跳舞、朗诵。 (1)小明可能抽到( ),也可能抽到( ),还可能抽到( )。有( )种可能。 (2)小明抽到了跳舞后,还剩下两张卡片,所以小丽可能抽到( ),也可能抽到( )。有( )种可能。 (3)小丽抽到朗诵后,只剩下一张卡片,所以小雪( )抽到唱歌。 (4)在一定的条件下,一些事件的结果是可以预知的,具有( )性,( )的事件用“( )”或“( )”来描述事件的结果。一些事件的结果是不可预知的,具有( )性,( )的事件用“( )”来描述事件的结果。 3.教材第45页例2。 (1)盒子里有( )种颜色的棋子,任意摸出一个棋子,可能是( )色,也可能是( )色,有( )种可能性。 (2)左边的小组摸出红色的棋子( )次,摸出蓝色的棋子( )次。 (3)右边的小组摸出红色的棋子( )次,摸出蓝色的棋子( )次。 (4)无论怎么摸,摸出( )色棋子的次数比( )色棋子的次数多。从而发现,事件发生的可能性有大有小,在总数中所占的数量越多,可能性就越( );所占数量越少,可能性就越( )。 4.教材第46页例3。 (1)盒子里有( )种颜色的球,任意摸出一个球,可能是( )色,也可能是( )色,有( )种可能性。 (2)观察记录表。 每个小组摸到( )球的次数多,摸到( )球的次数少,说明盒子里的( )球被摸到的可能性要大于( )球。 由此可知,盒子里( )球多,( )球少。从而发现,事件发生的可能性的大小与( )有关,事件发生的可能性越大,那么在总数中所占的数量就( );事件发生的可能性越小,所占数量越( )。
5.把2个绿球和3个红球(除颜色不同外其他完全相同)放入箱中,任意摸一个球,有( )种结果,摸到( )的可能性大。再放进4个黄球,有( )种结果,摸到( )的可能性大,( )摸到蓝球。
每日 口算 3.5×2= 0.2÷0.1= 0.24×5= 3.2÷8= 4.2×0.5= 1.2÷0.3= 0.5×100= 7.2÷9=
五 简 易 方 程
1 用字母表示数(1)
预习指南:能用字母表示数和数量关系,理解字母的取值范围,知道字母与数字相乘的简便写法,并会求含有字母的式子的值。
温故 知新 1.生活中,用字母CCTV表示( )。 扑克牌中,A、K、J、Q这些字母表示的数分别是( )。
2.教材第52页例1。 (1)根据“爸爸比小红大30岁”可知:当小红1岁时,爸爸的年龄是1+30=31(岁);当小红2岁时,爸爸的年龄是2+30=32(岁);当小红3岁时,爸爸的年龄是3+30=33(岁)……列表表示为 (2)用一个式子表示任何一年爸爸的年龄的方法。 方法一:用关系式表示。 根据“爸爸比小红大30岁”可以知道:爸爸的年龄=( )的年龄+( )岁。 方法二:用含有字母的式子表示。 如果用字母a表示小红的年龄,那么爸爸的年龄就可以用( )表示。 这里的a不能无限大,也不能是分数、小数等。 (3)代入求值:当a=11岁时,爸爸的年龄是( )岁。 3.教材第53页例2。 (1)根据“在月球上,人能举起物体的质量是地球上的6倍”可知:当人在地球上能举起1 kg的物体时,在月球上就能举起1×6=6(kg)的物体;当人在地球上能举起2 kg的物体时,在月球上就能举起2×6=12(kg)的物体……列表表示为
(2)用含有字母的式子表示人在月球上能举起物体的质量。 人在月球上能举起物体的质量=人在( )上能举起物体的质量×( ),如果用字母x表示人在地球上能举起物体的质量,那么人在月球上能举起物体的质量可表示为( )。这里的x应该是一个大于0而小于或等于人在地球上所能举起的极限质量。字母和数字相乘,乘号省略不写,一般把数写在字母的( )面。 (3)代入求值:当x=15时,图中小朋友在月球上能举起的物体的质量是( )kg。
4.填一填。 (1)阳光小学五年级有学生178人,星期三缺勤的有a人,出勤的有( )人。 (2)一箱苹果重20千克,b箱苹果重( )千克。 5.用含有字母的式子表示出x只青蛙的腿的数量是( ),当x=12时,这些青蛙有( )条腿。 6.你能用式子表示下面三角形的周长吗 (1)三角形的三条边分别长a、b、c。 (2)一个等腰三角形,底长a,一条腰长b。
每日 口算 1.5×4= 0.45÷0.15= 0.49÷7= 84÷4.2= 3.62×2= 0.2÷0.1= 0.24×5= 3.2÷8=
用字母表示数(2)
预习指南:能用字母表示运算定律及计算公式,理解一个数的平方的含义,知道乘号可以简写和略写,会代入公式计算。
温故 知新 1.省略乘号写出下列各式。 4×b= x×5= a×m= c×3= y×y= 2.(1)用v表示速度,t表示时间,s表示路程。s=( ) (2)乐乐每分钟走80 m,30分钟能走多少米
3.教材第54页例3。 (1)用字母表示运算定律。 运算定律用字母表示简便记法加法交换律—加法结合律—乘法交换律乘法结合律乘法分配律
(2)用字母表示计算公式。 ①如果用a表示正方形的边长,用S表示面积,用C表示周长。 正方形的周长公式用字母表示为( ),面积公式用字母表示为( )。a2读作( ),表示( )个( )相( )。 ②代入求值:当a=6时,计算正方形的周长和面积: C=( )=( )×( )=( )(cm) S=( )=( )×( )=( )(cm2)
4.根据运算定律在 里填上适当的数或字母。 (x+37)+63=x+( + ) (a+6)×b= · + · 2.4×a+b×2.4=( + )× 9x-5x=( - )x 5.先写出长方形的周长和面积计算公式,再计算。
每日 口算 8÷0.5= 0.32÷16= 0.5×1.1= 6÷1.2= 0.4÷8= 6.8÷1.7= 14÷0.7= 0.49÷0.7=
用字母表示数(3)
预习指南:用含有字母的式子表示数量关系,并能化简含有字母的式子。
温故 知新 1.把结果相同的两个式子连起来。 a2 4.5×4.5 x+x b×1 2x b 4.52 a×a
2.教材第58页例4。 (1)根据题意可以得到下面的数量关系式: 一大杯果汁的质量( )=还剩下果汁的质量 (2)每小杯果汁是x g,3小杯果汁是( )g,1大杯果汁是( )g,倒去3小杯果汁后,还剩下( )g。 (3)当x=200时,大杯中还剩下( )g果汁。1200-3x的差最小是( ),3x最大是( ),所以式子中x的值最大是( )。 3.教材第59页例5。 (1) (2)从上面两种数小棒的方法中可以得出:3x+4x=( )。 (3)当x=8时,一共用( )根小棒。
4.公园里有松树x棵,柳树的棵数比松树的5倍少8棵。 (1)用式子表示柳树的棵数。 (2)当x=25时,柳树有多少棵 5.用6根小棒摆1个平行四边形,5根小棒摆1个梯形。 (1)摆x个平行四边形和x个梯形,
一共用了多少根小棒 (2)当x=15时,一共用了多少根小棒
每日 口算 0.63÷9= 1.8×0.4= 26.5÷5= 3.1×0.3= 9÷5= 3.2÷1.6= 2.4×8= 7.6÷3.8=
2 方程的意义和等式的性质(1)
预习指南:理解方程的意义并会判断一个式子是否为方程。知道方程与等式的关系,并能用方程表示简单的数量关系。
项目 内容
温故 知新 1.填空。 20y-8y=( ) 17.5x-7.5x=( ) b-0.35b=( ) 6a+15a-3a=( )
2.教材第62页情境图。 (1)认识等式。 (2)认识方程。 ①空杯子的质量。 ②称一杯水的质量。 如果水重x g,那么杯子和水共重( )g;此时天平左边重,用式子表示为( )。天平右边增加一个100 g砝码,此时天平左边重,用式子表示为( );天平右边再增加一个100 g砝码,此时天平右边重,用式子表示为( );把一个100 g的砝码换成50 g,此时天平平衡,用式子表示为( )。
3.教材第63页情境图。 (1)每本练习本x元,3本练习本的总价可以表示为( )元,也就是2.4元,因此可列等式为( )。 (2)像100+x=250,3x=2.4……这样,含有( )的( )就是( )。判断一个式子是不是方程,一看是不是( ),二看有没有( )。 (3)你能自己写出一些方程吗
4.下面哪些式子是方程 在后面的括号里画“ ”。 x+3.6=7( ) a×2<2.4( ) 3-1.4=1.6( ) 3÷b( ) 8-x=2( ) 6.2÷2>3( ) 4×2.4=9.6( ) 2x+3y=9( ) 5.用方程表示下面的数量关系。
每日 口算 1.21÷11= 8.5÷1.7= 0.36÷4= 0.75×4= 53×0.01= 0.12×0.7= 0.92÷0.4= 0.32÷1.6=
方程的意义和等式的性质(2)
预习指南:理解等式的性质。
温故 知新 1.判断。(正确的画“ ”,错误的画“ ”) (1)含有未知数的式子叫做方程。 ( ) (2)所有的方程都是等式。 ( ) (3)2x-3=0不是方程。 ( )
2.教材第64页情境图。用含有字母的式子表示下面的数量关系。 (1) 1把茶壶的质量等于2个茶杯的质量,用等式表示为( ),在天平两边各增加1个同样的茶杯,天平仍然保持( ),用等式表示为( )。 (2) 1个花盆和1个花瓶的质量等于4个花瓶的质量,用等式表示为( ),在天平两边都拿掉1个花瓶,天平仍然保持( ),用等式表示为( ),即( )个花盆和( )个花瓶同样重。 (3)等式的性质1:等式两边( )或( )同一个数,左右两边仍然( )。 3.教材第65页情境图。用含有字母的式子表示下面的数量关系。 (1) 1瓶墨水的质量等于1个文具盒的质量,用等式表示为( ),左右两边的数量都扩大到原来的2倍,天平仍然保持( ),用等式表示为( )。 (2) 2个排球和6个皮球的质量相等,用等式表示为( ),将左右两边的球都平均分成2份,各去掉1份,天平仍然保持( ),用等式表示为( )。 (3)等式的性质2:等式两边乘同一个数,或除以同一个不为( )的数,左右两边仍然( )。
4.如果a=b,根据等式的性质填空。 a+6=b+( ) a-( )=b-8 a×2=b×( ) a÷( )=b÷3 a+c=b+( ) a×( )=b×c
每日 口算 1.44÷12= 18.2÷9.1= 4.5÷0.5= 8.1÷2.7= 2÷0.05= 3.2×0.2= 1.8×40= 4.27×0.1=
3 解方程(1)
预习指南:能运用等式的性质解方程,会正确解形如x±a=b、ax=b(a不等于0)、x÷a=b(a不等于0)、a-x=b、a÷x=b的方程。
温故 知新 1.如果x=y,根据等式的性质填空。 x-( )=y-a x+8=y+( ) x÷( )=y÷3.5 x×( )=y×c
2.教材第67页例1。 (1)一共有9个球,盒子里有x个,盒子外有3个。根据题意列方程为( )。 (2)根据等式的性质1,等式两边减去( ),左右两边仍然相等。天平演示: (3)规范书写。 x+3=9 解:x+3-( )=9-( ) 依据( ) x=( ) (4)使方程左右两边相等的( )的值,叫做方程的( )。求方程的解的过程叫做( )。方程的解是一个( ),而解方程是一个( )。 (5)检验。
方程左边=x+3
=( )+3
=( )
=方程右边
所以,( )是方程的解。 检验方法:把x的值代入方程的
( )边,然后检验方程的左
右两边的结果是否( ) 3.教材第68页例2。
3x=18
解:3x÷( )=18÷( ) 依据( )
x=( ) 4.教材第68页例3。
20-x=9
解:20-x+( )=9+( ) 依据( )
20=9+x
9+x=20
9+x-( )=20-( ) 依据( )
x=( )
5.解方程。 x+3.2=4.6 5x=6 18-x=3
每日 口算 10÷2.5= 0.3÷0.06= 0÷0.31= 4.2×4= 1.6×0.5= 0.12÷4= 9÷4.5= 0.24÷12=
解方程(2)
预习指南:把“ax”和“x±b”看成一个整体,解形如ax±b=c(a不等于0)和a(x±b)=c(a不等于0)的方程。
温故 知新 1.解方程。 2.4x=6 x-1.8=4 5.7÷x=3
2.教材第69页例4。 (1)已知1盒铅笔有x支,由题意列等量关系式为3盒铅笔的支数+( )支=( )支,列方程为( )。 (2)把3x看成一个整体,根据等式的性质1,在等式的两边同时减去( ),得到3x=( ),再根据等式的性质2解方程。 3x+4=40
解:3x+4-( )=40-( )依据( )
3x=36
3x÷( )=36÷( )依据( )
x=( ) 检验:
方程左边=3x+4
=
=
=
所以,x=( )是方程的解。 3.教材第69页例5。 2(x-16)=8 解: 2(x-16)÷( )=8÷( ) 把( )看作一个整体。 x-16=4 x-16+( )=4+( ) x=( ) 也可以这样解: 2(x-16)=8
解:2x-32=8 运用了( )律
2x-32+( )=8+( )
2x=40
2x÷( )=40÷( )
x=( )
4.根据题意列方程并求出方程的解。 (1) (2)
每日 口算 90÷4.5= 21.3×3= 0.1÷2= 0.21×4= 0.4×5= 1.4÷0.7= 1.6÷0.2= 4.8÷8=
4 实际问题与方程(一)
预习指南:能根据题中的等量关系列方程解决实际问题。知道列方程解决实际问题的步骤。
温故 知新 1.解方程。 x+19=51 2x=16.2 9x+36=72
2.教材第73页例1。 (1)已知小明的跳远成绩为4.21 m,超过原纪录0.06 m。由于原纪录是未知数,可以把它设为x m。 (2)根据题意写出数量关系式:( )+( )=( )。 (3)解:设学校原跳远记录是x m。 x+0.06=4.21 x+0.06-0.06=4.21-0.06 x=( ) 求出的未知数后面( )单位名称。(填“写”或“不写”) (4)检验。 方程左边=x+0.06 =( )+0.06 =( ) =方程右边 所以,( )是方程的解。 3.教材第74页例2。 (1)根据题意写出等量关系式:( )色皮的块数×2-4=( )色皮的块数。 (2)解:设共有x块黑色皮。 2x-4=20 2x-4+4=20+4←把( )看成一个整体。 2x=24 2x÷2=24÷2 x=( ) 答:共有( )块黑色皮。 (3)列方程解决实际问题的步骤: ①找出( ),用字母( )表示; ②分析实际问题中的( )关系,找出( )关系,列( ); ③( )并( )作答。
4.共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒
每日 口算 8.8÷0.2= 8.8×0.1= 1.08×1= 4÷0.5= 2÷0.4= 0.88÷0.44= 30÷0.15= 1.01×2=
5 实际问题与方程(二)
预习指南:理解实际问题中有关和、差、倍的数量关系,体验化归方法,选择合适的等量关系设未知数列方程。
温故 知新 1.解方程。 3x+4×2.5=46 x+2.5x=17.5 9x+11x=100
2.教材第77页例3。 (1)根据等量关系式“( )的总价+( )的总价=总价钱”列方程求解。 解:设苹果每千克x元。 2x+2.8×2=10.4
=
=
=
= 把2x看成一个整体,
求出方程的解 答: 。 (2)根据等量关系式“两种水果的单价和×2=总价钱”列方程求解。 解:设苹果每千克x元。 (2.8+x)×2=10.4
=
=
=
= 把x+2.8看成一个整体,
求出方程的解 答: 。 3.教材第78页例4。 (1)列出等量关系式:( )面积+( )面积=地球表面积。 (2)解:设( )面积为x亿平方千米,那么( )面积可以表示为2.4x亿平方千米。 x+2.4x=5.1 (1+2.4)x=5.1←运用了( )律 3.4x=5.1 3.4x÷3.4=5.1÷3.4 x=( ) 海洋面积:5.1-( )=( )(亿平方千米) 或2.4×( )=( )(亿平方千米) 答:陆地面积为 亿平方千米,海洋面积为 亿平方千米。
4.解决问题。 (1)一辆卡车今天计划运35吨货物,每次能运5吨。上午运了3次,下午要运几次才能运完 (2)妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和妈妈今年各多少岁
每日 口算 0.56×100= 9.5÷0.95= 7.2÷0.08= 12.8÷4= 3.2÷8= 7.2÷9= 84÷2= 72×0.01=
6 实际问题与方程(三)
预习指南:学会用画线段图等方法分析数量关系,用方程解决工程问题、行程问题、购物问题等一系列的实际问题,体会数学模型思想。
温故 知新 1.解方程。 5(x+1.5)=17.5 8(x-6.2)=41.6 6x+35×6=360
2.教材第79页例5。 (1)阅读与理解。 已知小林骑车的速度是( )米/分、小云骑车的速度是( )米/分,两家相距( )km,周日早上9:00两人分别从家骑自行车相向而行,求两人何时相遇。 (2)分析与解答。 ①画线段图,分析数量关系。 列出等量关系式:( )骑的路程+( )骑的路程=总路程。 ②列方程解决问题。 解:设( )。 0.25x+0.2x=4.5 0.45x=4.5←运用了( )律 0.45x÷( )=4.5÷( ) x=( ) 答:两人( )相遇。 (3)回顾与反思。 解决相遇问题时,可以先画( )分析数量之间的相等关系,再根据“相遇时间=( )÷( )”列方程解决。
3.解决问题。 (1)甲、乙两个工程队铺一条长1400 m的公路,他们从两端同时施工, 甲每天铺80 m,乙每天铺60 m,几天后能够铺完这条公路 (2)甲、乙两辆汽车同时从同一地点出发,相背而行,2.4小时后相距216千米。甲车的速度是42千米/时,求乙车的速度。
每日 口算 3÷0.05= 0.21÷0.7= 0.42÷10= 4.2÷0.7= 7.2÷0.4= 11÷0.1= 18÷0.2= 15÷0.5=
六 多边形的面积
1 平行四边形的面积
预习指南:利用数方格和割补法探索平行的四边形面积计算公式,并能正确计算。
温故 知新 1.画出下面平行四边形底边上的高。
2.教材第87页情境图。 要比较两个花坛的大小,需要先求出两个花坛的( )。观察花坛,一个是( )形,可以通过测量( )、( )计算出面积;一个是( )形,面积计算方法未知。 (1)数方格:一个方格代表1 m2,不满一格的都按半格计算。 (2)填表。 (3)它们的面积( )。 3.教材第88页情境图。 (1)把一个平行四边形沿( )剪开,通过割补平移转化成一个长方形。长方形的长相当于平行四边形的( ),长方形的宽相当于平行四边形的( ),拼出的长方形的面积与原来平行四边形的面积( )。 (2)比较发现:长方形的面积=( )×( ); 平行四边形的面积=( )×( )。 (3)如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成:( )。 4.教材第88页例1。 (1)花坛的形状是( ),要求花坛的面积,也就是求( )的面积。 (2)已知平行四边形的底和高,代入面积公式计算。 S=( )=( )×( )=( )(m2)
5.填表。 6.一个平行四边形的停车位,长是5 m,高是2.5 m,它的面积是多少
每日 口算 2.2÷2= 3.9÷3= 12.8÷4= 1.3×0.5= 1.7×0.2= 2.8÷0.4= 1.8×30= 169÷1000=
2 三角形的面积
预习指南:掌握三角形的面积计算公式,会计算三角形的面积。理解拼成的平行四边形和原来三角形的关系。
温故 知新 1.求下面平行四边形的面积。
2.教材第91页情境图。 (1)动手操作。 ①两个完全一样的( )三角形可以拼成一个( )形。 ②两个完全一样的( )三角形可以拼成一个( )形。 ③两个完全一样的( )三角形可以拼成一个( )形。 (2)观察发现。 把两个( )的三角形拼在一起,可以得到一个( )形,平行四边形的底等于三角形的( ),平行四边形的高等于三角形的( ),平行四边形的面积是其中一个三角形面积的( ),所以三角形的面积=平行四边形的面积÷( ),即三角形的面积=( )×( )÷( ),用字母表示为S=( )。 3.教材第92页例2。 (1)红领巾的形状是( ),要求它的面积,也就是求( )的面积。 (2)已知三角形的底和高,代入面积公式计算。 S=( )=( )×( )÷( )=( )(cm2)
4.求下面三角形的面积。
每日 口算 3.6÷1.8= 0.38+1.2= 0.36×20= 4-2.5= 17÷85= 2.8÷0.4= 0.27×3= 8×1.1=
3 梯形的面积
预习指南:掌握梯形的面积计算公式,能用梯形的面积公式解决实际问题。
温故 知新 1.写出梯形的各部分名称。
2.教材第95页情境图。 (1)拼摆法。 ①两个( )的梯形能拼成一个平行四边形。 ②梯形的( )等于平行四边形的( ),梯形的高等于平行四边形的( ),一个梯形的面积等于拼成的平行四边形面积的( )。 ③ (2)分割法。 ①将一个梯形分割成两个( )形。 梯形的面积=三角形①的面积+三角形②的面积 =( )×( )÷2+( )×( )÷2 =( + )×( )÷( ) ②将一个梯形分割成一个( )形和一个( )形。 梯形的面积=( )形面积+( )形面积 =( )+( ) =( + )×( )÷( ) (3)梯形的面积= ,如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式用字母表示为 。 3.教材第96页例3。 (1)我国三峡水电站大坝的横截面的一部分是( ),要求它的面积,也就是求( )的面积。 (2)已知梯形上底、下底和高,代入面积公式计算。 S=( )=( + )×( )÷( )=( )(m2)
4.计算下面梯形的面积。(单位:cm)
每日 口算 4.06×100= 16×0.2= 0.5÷0.2= 7÷0.5= 0.9÷4.5= 4.6×0.1= 0.35×2= 4.2÷2=
4 组合图形的面积
预习指南:计算组合图形的面积,关键是采用分割法、添补法等常用的方法,把组合图形转化成已学过的简单图形,再分别计算面积,最后相加、减。
温故 知新 1.用公式表示各图形的面积。 平行四边形的面积=( ); 三角形的面积=( ); 梯形的面积=( )。
2.教材第99页情境图。 (1)认识图形。 图中的图形分别是中队旗、房屋的一面墙、风筝和由七巧板拼成的一个( )形。 (2)观察发现。 中队旗由( )组合而成;小房子由( )组合而成;风筝由( )组合而成;七巧板拼成的长方形由( )组合而成。 (3)认识组合图形。 组合图形可以看成是由几个简单图形组合而成的。 3.教材第99页例4。 计算房子侧面墙的面积,可以将其看成是由几个简单图形组合而成的,再计算。 (1)可以把它看成是由一个( )形和一个( )形的组合的。 列式解答:
(2)可以把它分割成两个完全相同的( )形。 列式解答:
(3)求组合图形的面积时,可以把组合图形分割成若干个我们学过的图形,把各个图形的面积( );还可以把组合图形补成我们学过的简单图形,再减去补上的图形面积。
4.一面中国少年先锋队中队旗的面积是多少 (至少用两种方法) 5.一个指示牌的形状如下图,求它的面积。
每日 口算 1.2×20= 20.6-2.6= 6.5÷5= 40×0.4= 1.4×6= 12.5÷0.5= 1.3×0.7= 2.1÷0.03=
5 不规则图形的面积
预习指南:借助方格纸估算不规则图形的面积,并将不规则的图形转化成学过的图形进行估算。
温故 知新 1.数一数,算一算。
2.教材第100页例5。 (1)阅读与理解。 已知每个小方格的面积是1 cm2,要估计这片形状不规则的叶子的面积。 (2)分析与解答。 方法一:数方格。 在方格纸上描出叶子的轮廓图。图中的每个小方格表示( ),方格纸上满格的一共有( )格,不是满格的也有( )格,所以这片叶子的面积在( )cm2~( )cm2之间。如果把不满一格的都按半格计算,这片叶子的面积大约是( )cm2。 方法二:转化法。 将这片叶子的图形近似转化成平行四边形,底是( )cm,
高是( )cm,根据( )的面积计算公式,它的面积
大约是( )cm2。 (3)回顾与反思。 估算不规则图形的面积可以先通过( )确定面积的范围,再数一数满格的格数和不满格的格数;也可以( )为学过的图形来估算。
图中每个小方格的面积代表1 m2,
请你估计阴影部分的面积。
4.下面是一块近似三角形的荷塘,底是
56 m,高是30 m,这个荷塘的面积大约
是多少平方米
每日 口算 2.8×0.2= 14.8÷2= 4.5×0.6= 12.6÷3= 2.5×0.5= 12.3÷3= 8×0.09= 1.62÷2=
七 植 树 问 题
植 树 问 题
预习指南:运用画图策略理解并发现植树问题中间隔数和棵数的规律,解决生活中的实际问题。
温故 知新 1.一根木头平均截成6段,需要截几次
2.教材第106页例1。 (1)猜想。 在一条长100 m的小路一边植树,每隔5 m栽一棵,共栽100÷5=( )(棵)。 (2)验证。 ①20 m长的路,每隔5 m栽1棵(两端要栽),20 m里面有( )个5 m,要栽( )棵树。 ②25 m长的路,每隔5 m栽1棵(两端都栽),25 m里面有( )个5 m,要栽( )棵树。 …… ③在一条路的一边栽树,两端都栽时, 总长÷间距=( ),( )+( )=( )。 (3)解决问题:100÷5=20 20( )=( )(棵) 答:一共要栽 棵树。 3.教材第107页例2。 (1)画线段图理解间隔数与棵数的关系: 在一条线段上栽树,两端都不栽时,棵数=间隔数( )。 (2)解决问题:60÷3=20 20( )=( )(棵) ( )×2=( )(棵) 答:一共要栽 棵树。 4.教材第108页例3。 (1)假设周长是40 m,画图理解题意。 发现:圆形池塘可以看成封闭曲线,相当于只栽一端,间隔数棵数。 (2)解决问题:120÷10=( )(棵) 答:一共要栽 棵树。
5.有一条长160 m的路,工人们在路的一旁每隔2 m栽一棵树。如果两端都栽,则要栽( )棵;如果只栽一端,则要栽( )棵;如果两端都不栽,则要栽( )棵。 6.一根木头长10 m,要把它平均分成5段,每锯下一段需要8分钟,锯完一共需要多少分钟
每日 口算 2.5÷5= 4.5×0.1= 2.1÷0.7= 0.2×13= 0.4×5= 1.4÷0.7= 1.6÷0.2= 40.8÷8=
参考答案
一 小 数 乘 法
1 小数乘整数
1.35 3 105 60
2.3.5 3 3 3.5 加法 3.5 3.5 3.5 10.5 3.5 3 5 3.5 3 5 3 3 9 5 3 15 1 5 9 1 5 10 5 10.5 3.5 35 3.5 35 10.5 105 3.5 35 105 10.5
3. (1)100 100
(2)相同 整数 几 去掉
4.23 2 右 一
5.8.2 205 86.8 124
每日口算:1.2 1.5 3 8.4 1.4 8.6 7.7 0
2 小数乘小数(1)
1.4 7.7 9.2 0.1 3.8 6.6 3.6 9.9
2.2.4 0.8 0.9 面积 0.9
(1)1.92 10 10 100
(2)1.728 100 10 1000
(3)①小数点 ②因数 右边
(4)2.4×0.8=1.92(cm2)
1.92×0.9=1.728(kg)
答:一共需要1.728 kg油漆。
3.224 四 0.0224 0
4.两位 四位 三位
5.
每日口算:0.084 0.98 0.096 0.6 2.1 1
1.41 0.062
小数乘小数(2)
1.10 100 1 1 0.26 2 3 32
2.56千米/时 1.3 56 1.3 56×1.3
(1)①不对。 ②改正:
(2)
(3)56×1.3=72.8(千米/时)
答:鸵鸟的最高速度是72.8千米/时。
3.大 小
4.
每日口算:0.19 0.72 0.48 0.96 0.1 0.03 0.1 5.04
3 积的近似数
1.7 6.9 6.93 4 3.9 3.90 8 7.9 7.87
2.0.049 45 0.049 45 乘法 0.049×45
(1)四舍五入
(2)2.2 0 5
(3)积 下一位 四舍五入 约等 不能
(4)0.049×45≈2.2(亿个)
答:狗约有2.2亿个嗅觉细胞。
3.(1)0.72 百分 2 舍去 0.7
(2)0.765 千分 5 百分 进一 0.77
4.0.86×1.2≈1.03 2.34×0.15≈0.35
5.25×9.75≈244(元)
答:大约需要244元。
每日口算:1.05 0.085 1.3 1.41 0.54 0.294 0.1 0.9
4 整数乘法运算定律推广到小数
1. 25×95×4 25×32
=25×4×95 =25×4×8
=100×95 =100×8
=9500 =800
4×48+6×48 102×56
=(4+6)×48 =(100+2)×56
=10×48 =100×56+2×56
=480 =5600+112
=5712
2.a×b=b×a (a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
3.= = = 同样适用 简便
4.200 200+2 乘法分配
5. 4.8×0.25 1.5×105
=4×1.2×0.25 =1.5×(100+5)
=4×0.25×1.2 =1.5×100+1.5×5
=1.2 =157.5
45.2×99 1.2×2.5+0.8×2.5
=45.2×(100-1) =(1.2+0.8)×2.5
=45.2×100-45.2×1 =2×2.5
=4474.8 =5
2.33×0.5×4
=2.33×(0.5×4)
=2.33×2
=4.66
每日口算:84 0.108 0.96 0.642 0.6 1
10 1.5
5 解决问题(1)
1.7200 2000 1800 1000
2.(1)2 0.8 1 100
单价 数量 总价
大米 30.6元 2袋 —
肉 26.5元 0.8 kg —
鸡蛋 10元 1盒 —
20元 1盒
(2)62 99 60 20 100
(3)估大 估大 估小 估小
3. 2.8元<3元 3.9元<4元
4×3+6×4=36(元) 36元<50元
答:王阿姨付50元,够了。
4.12.3元>12元 18.6元>18元
4×12+2×18=84(元) 100-84=16(元)
16元<20元
答:剩下的钱不够买2个文具盒。
每日口算:1.62 1.2 0.7 0.8 2.7 0.072 0.1
0.096
解决问题(2)
1. 8+3.4×5 6.5-0.8×3.2
=8+17 =6.5-2.56
=25 =3.94
2.(1)7 1.5 7
(2)7 1.5 7+1.5×4=7+6=13(元)
(3)1.5 7 1.5×7=10.5(元)
7-1.5×3=2.5(元) 10.5+2.5=13(元)
3.7 8.5 10 11.5 13 14.5 16 17.5
4.5+(20-2)×1.2=26.6(元)
答:至少需要26.6元。
5.0.22+(8-3)×0.11=0.77(元)
答:她这一次通话的费用是0.77元。
每日口算:10 50 0.68 0.11 0.25 60 8.4
0.17
6 解 决 问 题
1.(1)四 0.55
(2)2.06 2.1
2.(1)2.5 2.5÷0.4
(2)6.25 2.4 0.1 7
(3)2.5÷0.4=6.25≈7(个)
答:需要准备7个瓶子。
3.(1)25 1.5 25÷1.5
(2)16.666… 25.5 0.5 16
(3)25÷1.5=16.666…≈16(个)
答:这些红丝带可以包装16个礼盒。
(4)进一 去尾
4.(1)5 (2)6 (3)7
5.38÷5≈8(辆)
答:需要准备8辆这样的小汽车。
每日口算:0.2 3 25.4 5 3 4 10 30
二 位 置
位 置
1.3 2(答案不唯一) 列 行
2.(1)左 右 前 后 列数 行数 逗号
(2)(2,3)
(3)(3,4)(4,3) 6 4
3.(1)3 0
(2)(3,5) (1,4) (2,2) (6,4) (3)略。
(4)列数 行数
4.(3,4) 5 2
5.(1)A(1,1) B(4,1) C(2,3)
(2)画图略。 A'(5,4) B'(8,4) C'(6,6)
每日口算:0.078 0.072 10.8 75 20.4 2050
2.22 0.206
三 小 数 除 法
1 除数是整数的小数除法
1.
2.(1)除 22.4÷4
(2)22400 22400 4 5600 5600 5.6
被除数 十分之一
(3)22.4÷4=5.6(km)
答:他平均每周应该跑5.6 km。
3.(1)除 28÷16
(2)十 百 整数 商 被除数 0 0
(3)28÷16=1.75(km)
答:平均每天慢跑1.75 km。
4.(1)除 5.6÷7
(2)0 5 6 0 相同 商 除数
(3)5.6÷7=0.8(km)
答:平均每天要跑0.8 km。
5. 7.83÷9=0.87 43.5÷29=1.5
14.21÷7=2.03 1.35÷15=0.09
6.(1)2.4÷2=1.2(元)
答:每块橡皮1.2元。
(2)4.8÷2=2.4
答:一套尺子的价钱是一个圆规价钱的2.4倍。
每日口算:0.6 0.6 1.4 3.4 0.3 0.3 0.3
1.7
2 一个数除以小数
1.2009 6 扩大 1000
2.133 37.2
3.(1)7.65 0.85 除 7.65÷0.85 (2)765 85 9 100 85 100 765 765 85 9
(3)7.65÷0.85=9(个)
答:这些丝绳可以编9个“中国结”。
4.45 0
(1)100 28 100 商不变 0 两
(2)①除数 整数 ②除数 被除数 0
③整数
5.
每日口算:2 9 1.3 12 0.8 8 1.1 0.5
3 商的近似数
1.1 1.0 0.99 4 4.5 4.50 3 3.1 3.09
2.(1)总价 数量 除法 19.4÷12
(2)
①1.62 三 分 ②1.6 二 角
(3)一 四舍五入 不能
(4)19.4÷12≈1.62(元)
答:每个大约1.62元。
或19.4÷12≈1.6(元)
答:每个大约1.6元。
3.
每日口算:2 30 200 2.5 2.3 0.6 0.4 1.3
4 循 环 小 数
1.4÷7≈0.57 16÷3≈5.33 2÷9≈0.22
2.(1)路程 时间 除 400÷75
(2)
25 3
(3)400÷75=5.333…(米)
答:平均每秒跑5.333…米。
3.(1)10 5
(2)5 6 4 5
(3)重复 循环 重复 循环节
(4)5. 0.0
(5)有限 无限
4.7.234 5.051 3.646
5.> < >
每日口算:0.7 0.6 0.6 0.9 0.06 0.4 100
1.1
5 用计算器探索规律
1.(1)2.0
(2)0.25 0.16
2.(1)0.2727… 0.3636… 0.4545…
(2)09 18 0.2727… 27
0.3636… 36 0.4545… 45 9
(3)0.5454… 0.6363… 0.7272… 0.8181…
(4)计算 规律 规律 结果 算式
3.(1)3.333 3.3333 3.33333
(2)0. 0. 0.
(3)1111.2222 11111.22222 111111.222222
4.0.444… 0.555… 0.777…
5.444.222 4444.2222
每日口算:0.046 30 50 8 300 30 300 30
四 可 能 性
可 能 性
1.可能 可能
2.(1)唱歌 跳舞 朗诵 3
(2)唱歌 朗诵 2
(3)一定
(4)确定 确定 一定 不可能 不确定 不确定
可能
3.(1)两 红 蓝 两
(2)14 6
(3)17 3
(4)红 蓝 大 小
4.(1)两 红 黄 两
(2)红 黄 红 黄 红 黄 数量 多 少
5.两 红 3 黄 不可能
每日口算:7 2 1.2 0.4 2.1 4 50 0.8
五 简 易 方 程
1 用字母表示数(1)
1. 中国中央电视台 1 13 11 12
2.(1)2+30=32 3+30=33
(2)小红 30 a+30 (3)41
3.(1)2×6=12 3×6=18
(2)地球 6 x×6 前
(3)90
4.(1)178-a
(2)20b
5. 4x 48
6. (1)a+b+c (2)2b+a
每日口算:6 3 0.07 20 7.24 2 1.2 0.4
用字母表示数(2)
1. 4b 5x am 3c y2
2.(1)vt
(2)80×30=2400(m)
答:30分钟能走2400米。
3.(1)a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a a·b=b·a或ab=ba
(a×b)×c=a×(b×c) (a·b)·c=a·(b·c)或(ab)c=a(bc)
(a+b)×c=a×c+b×c
(a+b)·c=a·c+b·c或(a+b)c=ac+bc 省略
(2)①C=4a S=a2 a的平方 2 a 乘
②4a 4 6 24 a2 6 6 36
4. 37 63 a b 6 b a b 2.4 9 5
5.C=(a+b)×2=(8+3)×2=22(cm)
S=ab=8×3=24(cm2)
每日口算:16 0.02 0.55 5 0.05 4 20 0.7
用字母表示数(3)
1.连线略。a2=a×a 4.5×4.5=4.52 x+x=2x b×1=b
2.(1)- 3小杯果汁的质量
(2)3x 1200 1200-3x
(3)600 0 1200 400
3.(1)3 3x 4 4x 7 7x 3x+4x (2)7x
(3)56
4.(1)5x-8
(2)5x-8=5×25-8=117
答:柳树有117棵。
5.(1)11x
(2)11x=11×15=165
答:一共用了165根小棒。
每日口算:0.07 0.72 5.3 0.93 1.8 2 19.2 2
2 方程的意义和等式的性质(1)
1.12y 10x 0.65b 18a
2.(1)50 50 100 等式
(2)①100 ②100+x 100+x>100
100+x>200 100+x<300 100+x=250
3.(1)3x 3x=2.4
(2)未知数 等式 方程 等式 未知数
(3)略。
4. x+3.6=7 8-x=2 2x+3y=9
5. 4x=16.8 x+129=288
每日口算:0.11 5 0.09 3 0.53 0.084 2.3 0.2
方程的意义和等式的性质(2)
1.(1) (2) (3)
2.(1)a=2b 平衡 a+b=2b+b
(2)a+b=4b 平衡 a+b-b=4b-b 1 3
(3)加上 减去 相等
3.(1)a=b 平衡 2a=2b
(2)2a=6b 平衡 2a÷2=6b÷2
(3)0 相等
4.6 8 2 3 c c
每日口算:0.12 2 9 3 40 0.64 72 0.427
3 解方程(1)
1.a 8 3.5 c
2.(1)x+3=9
(2)3
(3)3 3 等式的性质1 6
(4)未知数 解 解方程 值 过程
(5)6 9 左 相等 x=6
3.3 3 等式的性质2 6
4.x x 等式的性质1 9 9 等式的性质1 11
5. x+3.2=4.6
解:x+3.2-3.2=4.6-3.2
x=1.4 5x=6
解:5x÷5=6÷5
x=1.2
18-x=3
解:18-x+x=3+x
3+x-3=18-3
x=15
每日口算:4 5 0 16.8 0.8 0.03 2 0.02
解方程(2)
1. 2.4x=6
解:2.4x÷2.4=6÷2.4
x=2.5 x-1.8=4
解:x-1.8+1.8=4+1.8
x=5.8
5.7÷x=3
解:5.7÷x×x=3×x
3x÷3=5.7÷3
x=1.9
2.(1)4 40 3x+4=40
(2)4 36 4 4 等式的性质1 3 3 等式的性质2 12
3×12+4 40 方程右边 12
3.2 2 x-16 16 16 20 乘法分配 32 32
2 2 20
4. (1) 2x+48=102
解:2x+48-48=102-48
2x÷2=54÷2
x=27 (2)2(x+25)=76
解:2(x+25)÷2 =76÷2
x+25-25=38-25
x=13
每日口算:20 63.9 0.05 0.84 2 2 8 0.6
4 实际问题与方程(一)
1. x+19=51
解:x+19-19=51-19
x=32 2x=16.2
解:2x÷2=16.2÷2
x=8.1
9x+36=72
解:9x+36-36=72-36
9x÷9=36÷9
x=4
2.(2)原纪录 超出部分 小明的成绩
(3)4.15 不写 (4)4.15 4.21 x=4.15
3.(1)黑 白
(2)2x 12 12
(3)①未知数 x ②数量 等量 方程
③解方程 检验
4.解:设一共装了x筒。
5x+3=1428
x=285
答:一共装了285筒。
每日口算:44 0.88 1.08 8 5 2 200 2.02
5 实际问题与方程(二)
1. 3x+4×2.5=46
解:3x+10-10=46-10
3x÷3=36÷3
x=12
x+2.5x=17.5
解: 3.5x=17.5
3.5x÷3.5=17.5÷3.5
x=5 9x+11x=100
解:20x=100
x=5
2.(1)苹果 梨
2x+5.6=10.4
2x+5.6-5.6=10.4-5.6
2x÷2=4.8÷2
x=2.4
答:苹果每千克2.4元。
(2) (2.8+x)×2÷2=10.4÷2
2.8+x=5.2
2.8+x-2.8=5.2-2.8
x=2.4
答:苹果每千克2.4元。
3.(1)陆地 海洋
(2)陆地 海洋 乘法分配 1.5 1.5 3.6 1.5 3.6 1.5 3.6
4.(1)解:设下午要运x次才能运完。
5(3+x)=35
x=4
答:下午要运4次才能运完。
(2)解:设小明今年x岁,则妈妈今年3x岁。
3x-x=24
x=12
3x=36
答:小明今年12岁,妈妈今年36岁。
每日口算:56 10 90 3.2 0.4 0.8 42 0.72
6 实际问题与方程(三)
1. 5(x+1.5)=17.5
解:5(x+1.5)÷5=17.5÷5
x+1.5-1.5=3.5-1.5
x=2
8(x-6.2)=41.6
解:8(x-6.2)÷8=41.6÷8
x-6.2+6.2=5.2+6.2
x=11.4
6x+35×6=360
解:6x+210-210=360-210
6x÷6=150÷6
x=25
2.(1)250 200 4.5
(2)小林 小云
两人x分钟后相遇
乘法分配 0.45 0.45 10 9:10
(3)线段图 路程 速度和
3.(1)解:设x天后能够铺完这条公路。
80x+60x=1400
x=10
答: 10天后能够铺完这条公路。
(2)解:设乙车的速度是x千米/时。
2.4x+42×2.4=216
x=48
答: 乙车的速度是48千米/时。
每日口算:60 0.3 0.042 6 18 110 90 30
六 多边形的面积
1 平行四边形的面积
1.画法不唯一。
2.面积 长方 长 宽 平行四边
(2)6 m 4 m 24 m2 6 m 4 m 24 m2
(3)相等
3.(1)高 底 高 相等
(2)长 宽 底 高
(3)S=ah
4.(1)平行四边形 平行四边形
(2)ah 6 4 24
5.(竖排)798 21.5 5.2
6.5×2.5=12.5(m2)
答:它的面积是12.5 m2。
每日口算:1.1 1.3 3.2 0.65 0.34 7 54 0.169
2 三角形的面积
1.24×40=960(cm2)
2.(1)①锐角 平行四边 ②钝角 平行四边
③直角 平行四边
(2)完全相同 平行四边 底 高 2倍 2 底 高 2 ah÷2
3.(1)三角形 三角形
(2)ah÷2 100 33 2 1650
4.8×9.2÷2=36.8(cm2) 14×15÷2=105(cm2)
10×18÷2=90(dm2)
每日口算:2 1.58 7.2 1.5 0.2 7 0.81 8.8
3 梯形的面积
1.上底 下底 腰 高
2.(1)①完全相同 ②上底加下底 底 高 一半
(2)①三角 上底 高 下底 高 上底 下底 高
2 ②平行四边 三角 平行四边 三角 上底×高
(下底-上底)×高÷2 上底 下底 高 2
(3)(上底+下底)×高 ÷2 S=(a+b)×h÷2
3.(1)梯形 梯形
(3)(a+b)×h÷2 36 120 135 2 10530
4. (12+18)×9÷2
=30×9÷2
=135(cm2)
(7.2-1.6-2.2+7.2)×4.8÷2
=10.6×4.8÷2
=25.44(cm2)
每日口算:406 3.2 2.5 14 0.2 0.46 0.7 2.1
4 组合图形的面积
1.底×高 底×高÷2 (上底+下底)×高÷2
2.(1)长方 (2)2个梯形 三角形和正方形 4个三角形 5个三角形、1个正方形和1个平行四边形
3.(1)正方 三角 5×5+5×2÷2=30(cm2)
(2)梯 (5+5+2)×2.5÷2×2=30(cm2)
(3)相加
4.第一种方法:
30×2×80-30×2×20÷2=4200(cm2)
第二种方法:
(80+80-20)×30÷2×2=4200(cm2)
答:一面中国少年先锋队中队旗的面积是4200 cm2。
5. 20×10+10×20÷2=300(cm2)
答:它的面积为300 cm2。
每日口算:24 18 1.3 16 8.4 25 0.91 70
5 不规则图形的面积
1.3 2 6 2 4 8
2.(2)1 cm2 18 18 18 36 27 5 6 平行四边形 30
(3)数方格 转化
3.答案不唯一。30 m2
4.56×30÷2=840(m2)
答:这个荷塘的面积大约是840平方米。
每日口算:0.56 7.4 2.7 4.2 1.25 4.1 0.72
0.81
七 植 树 问 题
植 树 问 题
1.5次
2.(1)20 (2)①4 5 ②5 6
③间隔数 间隔数 1 棵数
(3)+ 1 21 21
3.(1)- 1
(2)- 1 19 19 38 38
4.(1)=
(2)12 12
5.81 80 79
6.(5-1)×8=32(分)
答:锯完一共需要32分钟。
每日口算:0.5 0.45 3 2.6 2 2 8 5.1
