19.1.1变量与函数(2)
文档属性
| 名称 | 19.1.1变量与函数(2) |  | |
| 格式 | zip | ||
| 文件大小 | 701.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-10 10:09:55 | ||
图片预览





文档简介
课件16张PPT。八年级 下册19.1.1 变量与函数(2)复习: 函数的定义:
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x =a 时,对应的 y =b,
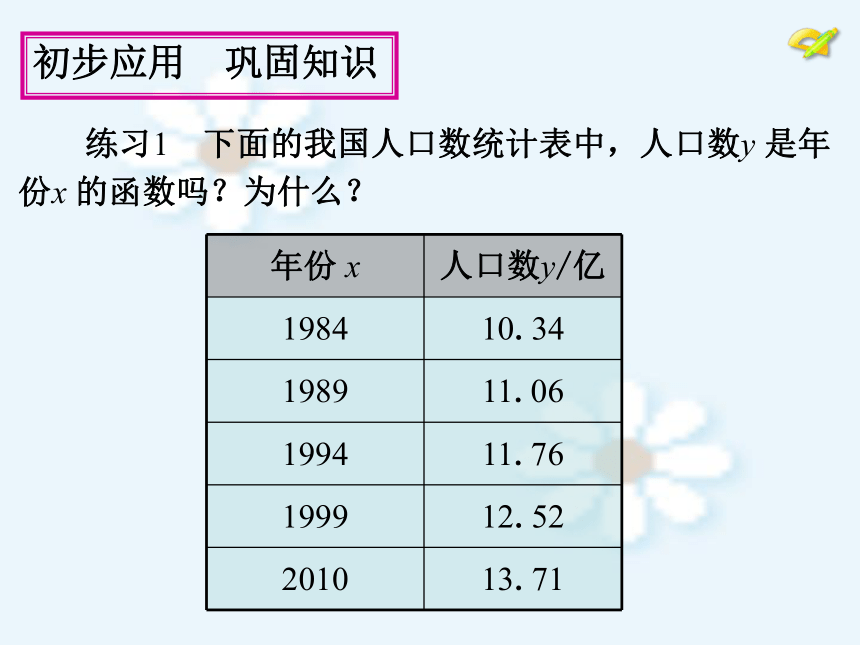
那么 b 叫做当自变量的值为 a 时的函数值. 初步应用 巩固知识 练习1 下面的我国人口数统计表中,人口数y 是年
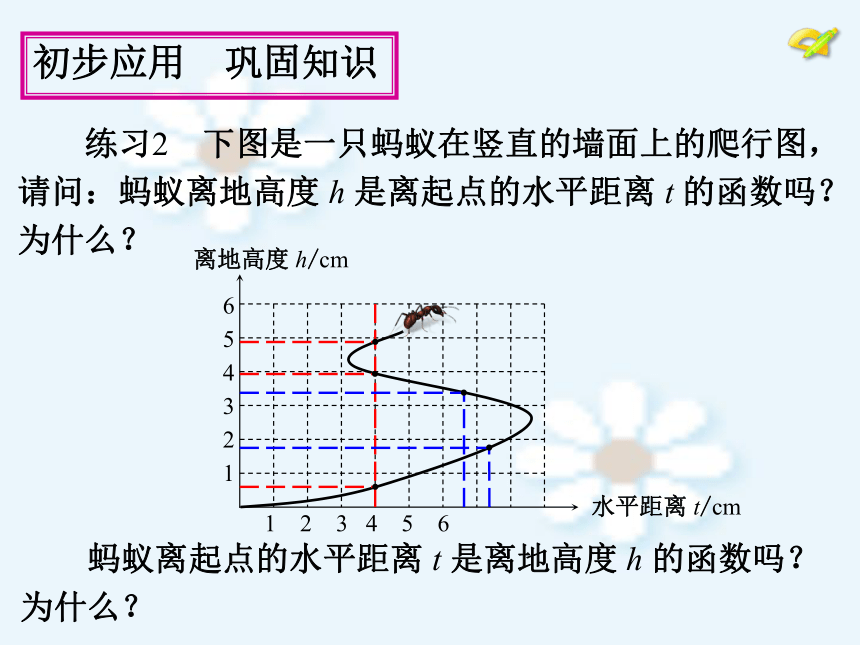
份x 的函数吗?为什么? 练习2 下图是一只蚂蚁在竖直的墙面上的爬行图,
请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗?
为什么? 蚂蚁离起点的水平距离 t 是离地高度 h 的函数吗?
为什么?水平距离 t/cm 离地高度 h/cm 1 2 3 4 5 6 6
5
4
3
2
1初步应用 巩固知识回顾总结 反思提升 谈谈你对函数有什么认识? 问题1 请用含自变量的式子表示下
列问题中的函数关系:
(1)汽车以60 km/h 的速度匀速行驶,行驶的时间
为 t(单位:h),行驶的路程为 s(单位:km);
(2)多边形的边数为 n,内角和的度数为 y. 函数的定义是,某一变化过程中有两个变量x,y,
对于变量x 每取一个确定的值,y 都有唯一确定的值与
之对应. 问题1(1)中,t 取-2 有实际意义吗? 问题1(2)中,n 取2 有意义吗?想一想说一说 根据刚才问题的思考,你认为函数的自变量可以取
任意值吗?
在实际问题中,函数的自变量取值范围往往是有限
制的,在限制的范围内,函数才有实际意义;超出这个
范围,函数没有实际意义,我们把这种自变量可以取的
数值范围叫函数的自变量取值范围. 确定自变量的取值范围时,不仅要考虑使函数关系
式有意义,而且还要注意问题的实际意义.练一练 问题2 你能用含自变量的式子表示下列函数,并
说出自变量的取值范围吗?
(1)等腰三角形的面积为12,底边长为 x,底边上
的高为 y,y 随着 x 的变化而变化;
(2)把边长为10 cm 的正方形纸板的四个角都截去
一个边长为 x 的小正方形,做成一个无盖的长方体,该
长方体的体积 V(单位:cm3)随 x(单位:cm)的变化
而变化. 做一做 例1 一辆汽车油箱中现有汽油50 L,它在高速公
路上匀速行驶时每千米的耗油量固定不变.行驶了100
km 时,油箱中剩下汽油40 L.假设油箱中剩下的油量
为 y(单位:L),已行驶的里程为 x(单位:km) .
(1)在这个变化过程中,y 是x 的函数吗?
(2)能写出表示 y 与 x 的函数关系的式子吗?
(3)这个变化过程中,自变量 x 的取值范围是什么?
(4)汽车行驶了200 km 时,油箱中还剩下多少汽油?
行驶了320 km 呢?做一做 用关于自变量的数学式子表示函数与自变量之间的
关系,是描述函数的常用方法.这种式子叫做函数的解
析式. 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
他测量出把油烧沸腾所需要的时间是160 s,这样就
可以确定该食用油的沸点温度.他是怎样计算的呢?做一做列表法、解析法做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(1)在这个测量过程中,锅中油的温度w 是加热时
间t 的函数吗?做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(2)能写出w 与t 的函数解析式吗? 做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(3)求这种食用油沸点的温度. (1)什么叫函数?
(2)本课学习了哪些表示函数的方法?
(3)在实际问题中,函数的自变量取值往往是有限
制的,怎样确定由实际问题抽象出的函数的自
变量取值范围?课堂小结 作业:讲学稿上的相关练习。课后作业
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x =a 时,对应的 y =b,
那么 b 叫做当自变量的值为 a 时的函数值. 初步应用 巩固知识 练习1 下面的我国人口数统计表中,人口数y 是年
份x 的函数吗?为什么? 练习2 下图是一只蚂蚁在竖直的墙面上的爬行图,
请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗?
为什么? 蚂蚁离起点的水平距离 t 是离地高度 h 的函数吗?
为什么?水平距离 t/cm 离地高度 h/cm 1 2 3 4 5 6 6
5
4
3
2
1初步应用 巩固知识回顾总结 反思提升 谈谈你对函数有什么认识? 问题1 请用含自变量的式子表示下
列问题中的函数关系:
(1)汽车以60 km/h 的速度匀速行驶,行驶的时间
为 t(单位:h),行驶的路程为 s(单位:km);
(2)多边形的边数为 n,内角和的度数为 y. 函数的定义是,某一变化过程中有两个变量x,y,
对于变量x 每取一个确定的值,y 都有唯一确定的值与
之对应. 问题1(1)中,t 取-2 有实际意义吗? 问题1(2)中,n 取2 有意义吗?想一想说一说 根据刚才问题的思考,你认为函数的自变量可以取
任意值吗?
在实际问题中,函数的自变量取值范围往往是有限
制的,在限制的范围内,函数才有实际意义;超出这个
范围,函数没有实际意义,我们把这种自变量可以取的
数值范围叫函数的自变量取值范围. 确定自变量的取值范围时,不仅要考虑使函数关系
式有意义,而且还要注意问题的实际意义.练一练 问题2 你能用含自变量的式子表示下列函数,并
说出自变量的取值范围吗?
(1)等腰三角形的面积为12,底边长为 x,底边上
的高为 y,y 随着 x 的变化而变化;
(2)把边长为10 cm 的正方形纸板的四个角都截去
一个边长为 x 的小正方形,做成一个无盖的长方体,该
长方体的体积 V(单位:cm3)随 x(单位:cm)的变化
而变化. 做一做 例1 一辆汽车油箱中现有汽油50 L,它在高速公
路上匀速行驶时每千米的耗油量固定不变.行驶了100
km 时,油箱中剩下汽油40 L.假设油箱中剩下的油量
为 y(单位:L),已行驶的里程为 x(单位:km) .
(1)在这个变化过程中,y 是x 的函数吗?
(2)能写出表示 y 与 x 的函数关系的式子吗?
(3)这个变化过程中,自变量 x 的取值范围是什么?
(4)汽车行驶了200 km 时,油箱中还剩下多少汽油?
行驶了320 km 呢?做一做 用关于自变量的数学式子表示函数与自变量之间的
关系,是描述函数的常用方法.这种式子叫做函数的解
析式. 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
他测量出把油烧沸腾所需要的时间是160 s,这样就
可以确定该食用油的沸点温度.他是怎样计算的呢?做一做列表法、解析法做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(1)在这个测量过程中,锅中油的温度w 是加热时
间t 的函数吗?做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(2)能写出w 与t 的函数解析式吗? 做一做 例2 小明想用最大刻度为100℃的温度计测量食用
油的沸点温度(远高于100℃),显然不能直接测量,
于是他想到了另一种方法,把常温10℃的食用油放在锅
内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一
次油温,共测量了4次,测得的数据如下:
请你按下面的问题进行思考:
(3)求这种食用油沸点的温度. (1)什么叫函数?
(2)本课学习了哪些表示函数的方法?
(3)在实际问题中,函数的自变量取值往往是有限
制的,怎样确定由实际问题抽象出的函数的自
变量取值范围?课堂小结 作业:讲学稿上的相关练习。课后作业
