19.1.2函数的图象
图片预览





文档简介
课件21张PPT。八年级 下册19.1.2 函数的图象 问题1 函数图象是坐标平面上以自变量的值为横坐
标、以对应的函数值为纵坐标的点组成的曲线,函数图
象直观地反映了变量之间的对应关系和变化规律.那么,
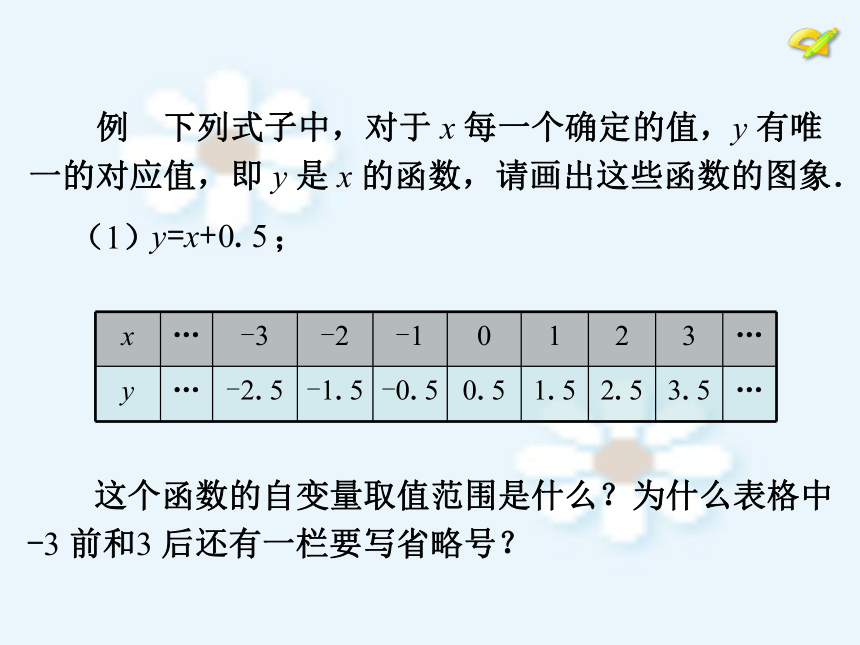
怎样画一个函数的图象呢? 例 下列式子中,对于 x 每一个确定的值,y 有唯
一的对应值,即 y 是 x 的函数,请画出这些函数的图象. 这个函数的自变量取值范围是什么?为什么表格中
-3 前和3 后还有一栏要写省略号? 例 下列式子中,对于 x 每一个确定的值,y 有唯
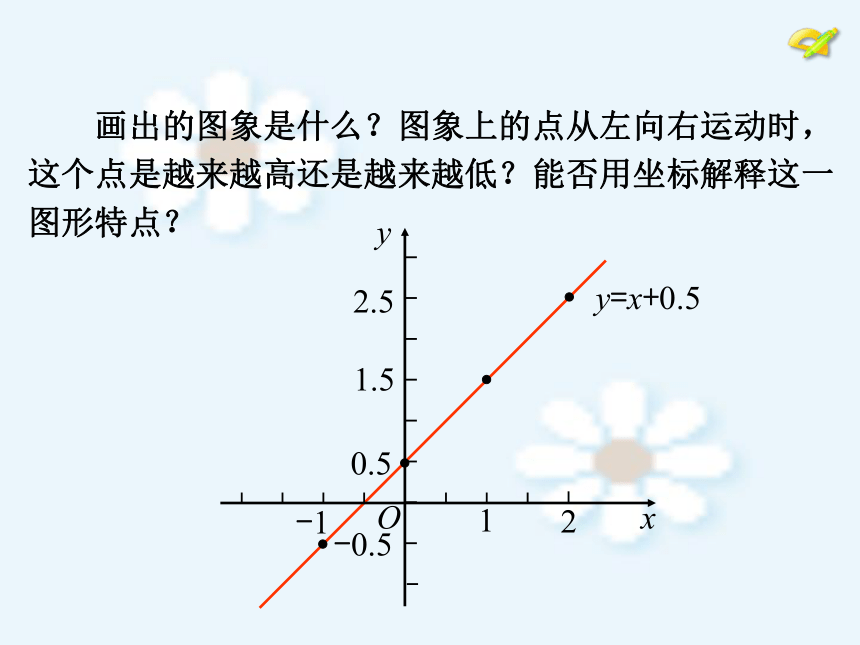
一的对应值,即 y 是 x 的函数,请画出这些函数的图象.(1) ; 画出的图象是什么?图象上的点从左向右运动时,
这个点是越来越高还是越来越低?能否用坐标解释这一
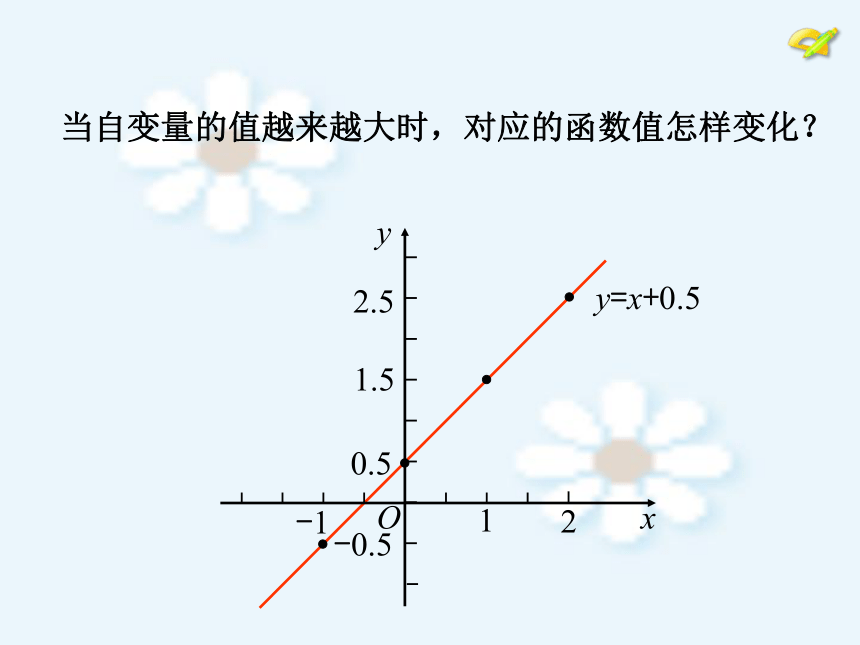
图形特点? 当自变量的值越来越大时,对应的函数值怎样变化? 归纳:
画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.练习练习 我们知道,函数图象是以自变量的值和对应的函数
值分别为横、纵坐标的点组成的图形,这样的点有无数
个,那么怎样判断一个点是否在函数图象上? 图象特征 ——坐标特征 ——变量的变化规律和变化趋势 思考 怎样从图象的特征分析中发现函数变化规律和变化
趋势?(1)函数图象上的点的横纵坐标分别表示什么?
(2)画函数图象时,怎样体现函数的自变量取值范围?
(3)用描点法画函数图象按照哪些步骤进行?
(4)怎样从图象上看出当自变量增大时,对应的函数
值是增大还是减小?课堂小结 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
(4)能画出函数的图象吗?y 是 x 的函数,自变量 x 的取值范围是x>0. 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围; y =2(x + ) 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(2)能求出这个问题的函数解析式吗? 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系; 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(4)能画出函数的图象吗?403530252015105510Oxy 合作探究:
说说函数的三种表示方法各有什么优点和不足,分
小组讨论一下.思考 (1)对于每一个大于0 的自变量的值,想准确确定
对应的函数值,用什么表示法较好?
(2)对于x 的值分别为1,2,3,4,5,6 时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x 的值增大时,函数值y 怎样变化,用
什么表示方法较好? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么
规律? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(3)据估计这种上涨规律还会持续2 h,预测再过2 h
水位高度将达到多少米.(1)函数有哪几种表示方法?这些表示方法分别有
哪些优势和不足?
(2)怎样根据函数分析变量的变化规律和变化趋势?
(3)当我们无法直接得到某一运动变化过程的函数
解析式时,我们可以通过哪些步骤的研究,得
到函数解析式,把握变化规律,预测变化趋势?课堂小结作业:
1、 讲学稿相关练习。
2、画出下列函数的图象,并指出当x 的值增大时,
函数值怎样变化?
(1)y=4-2x ; (2)y=-2x2+1.课后作业
标、以对应的函数值为纵坐标的点组成的曲线,函数图
象直观地反映了变量之间的对应关系和变化规律.那么,
怎样画一个函数的图象呢? 例 下列式子中,对于 x 每一个确定的值,y 有唯
一的对应值,即 y 是 x 的函数,请画出这些函数的图象. 这个函数的自变量取值范围是什么?为什么表格中
-3 前和3 后还有一栏要写省略号? 例 下列式子中,对于 x 每一个确定的值,y 有唯
一的对应值,即 y 是 x 的函数,请画出这些函数的图象.(1) ; 画出的图象是什么?图象上的点从左向右运动时,
这个点是越来越高还是越来越低?能否用坐标解释这一
图形特点? 当自变量的值越来越大时,对应的函数值怎样变化? 归纳:
画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.练习练习 我们知道,函数图象是以自变量的值和对应的函数
值分别为横、纵坐标的点组成的图形,这样的点有无数
个,那么怎样判断一个点是否在函数图象上? 图象特征 ——坐标特征 ——变量的变化规律和变化趋势 思考 怎样从图象的特征分析中发现函数变化规律和变化
趋势?(1)函数图象上的点的横纵坐标分别表示什么?
(2)画函数图象时,怎样体现函数的自变量取值范围?
(3)用描点法画函数图象按照哪些步骤进行?
(4)怎样从图象上看出当自变量增大时,对应的函数
值是增大还是减小?课堂小结 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
(4)能画出函数的图象吗?y 是 x 的函数,自变量 x 的取值范围是x>0. 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围; y =2(x + ) 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(2)能求出这个问题的函数解析式吗? 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系; 问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(4)能画出函数的图象吗?403530252015105510Oxy 合作探究:
说说函数的三种表示方法各有什么优点和不足,分
小组讨论一下.思考 (1)对于每一个大于0 的自变量的值,想准确确定
对应的函数值,用什么表示法较好?
(2)对于x 的值分别为1,2,3,4,5,6 时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x 的值增大时,函数值y 怎样变化,用
什么表示方法较好? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么
规律? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗? 例 一水库的水位在最近5 h 内持续上涨,下表记录
了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表
示水位高度.
(3)据估计这种上涨规律还会持续2 h,预测再过2 h
水位高度将达到多少米.(1)函数有哪几种表示方法?这些表示方法分别有
哪些优势和不足?
(2)怎样根据函数分析变量的变化规律和变化趋势?
(3)当我们无法直接得到某一运动变化过程的函数
解析式时,我们可以通过哪些步骤的研究,得
到函数解析式,把握变化规律,预测变化趋势?课堂小结作业:
1、 讲学稿相关练习。
2、画出下列函数的图象,并指出当x 的值增大时,
函数值怎样变化?
(1)y=4-2x ; (2)y=-2x2+1.课后作业
