分式的加减(二)[下学期]
文档属性
| 名称 | 分式的加减(二)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 34.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-04 00:00:00 | ||
图片预览

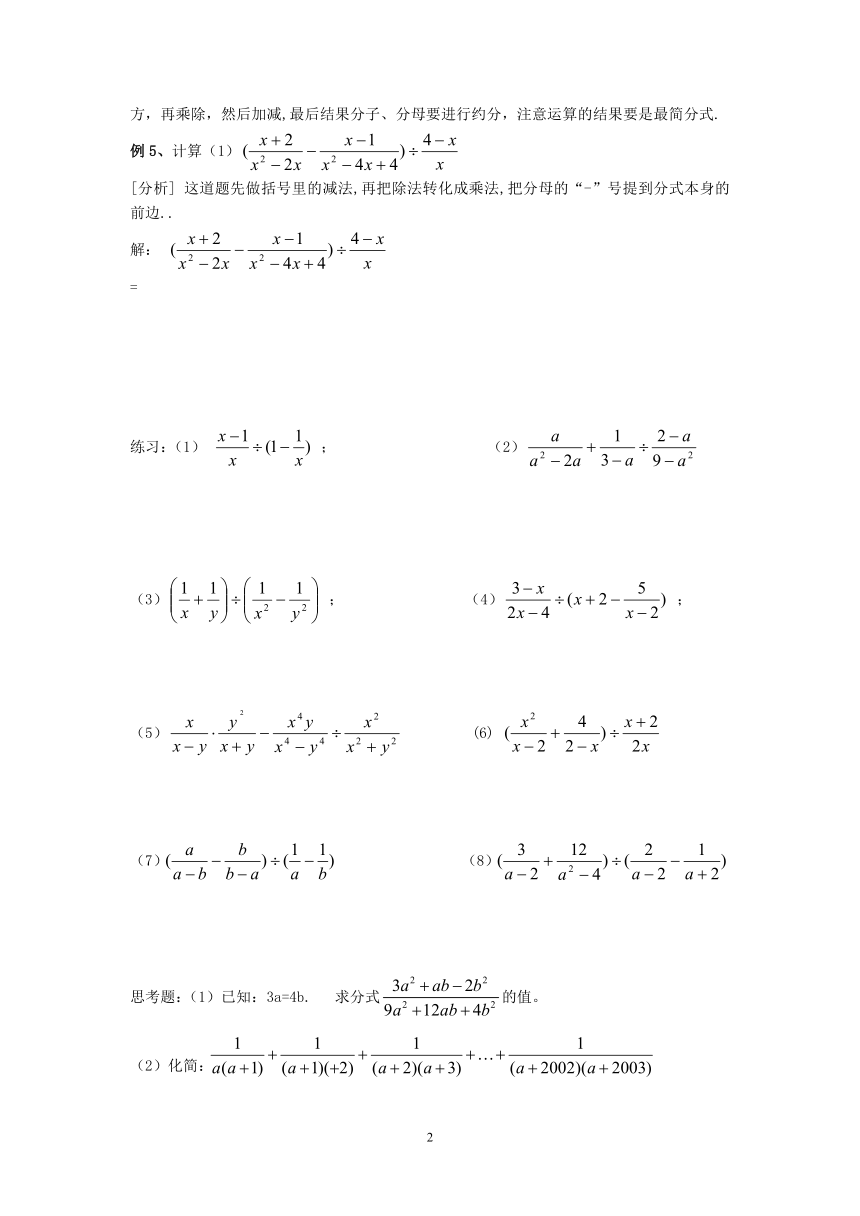
文档简介
分式的加减二及混合运算
1、知道负整数指数幂=(a≠0,n是正整数).
2、掌握整数指数幂的运算性质.
3、会用科学计数法表示小于1的数.
4、明确分式混合运算的顺序,熟练地进行分式的混合运算
一、整数指数幂的运算性质:
(1)同底数的幂的乘法:(m,n是整数,当m或n为负整数时,);
(2)幂的乘方:(m,n是整数,当m或n为负整数时,);
(3)积的乘方:(n是整数,当n为负整数时,,);
(4)同底数的幂的除法:( a≠0,m ,n是整数);
(5)商的乘方:(n是整数,,n为负整数时,);
例1:计算 (1) (2)
(3) (3×10-8)×(4×103) (4) (2×10-3)2÷(10-3)3
1.填空
(1)-22= (2)(-2)2= (3)(-2) 0=
(4)20= ( 5)2 -3= ( 6)(-2) -3=
(7) (8) ()
例2、下列等式是否正确?为什么?
(1) (2)
例3、纳米是非常小的长度单位,1纳米=米,把1纳米的物体放到乒乓球上,就如同把乒乓球放到地球上.1立方毫米的空间可以放多少个1立方纳米的物体?
例4、计算
[分析] 这道题是分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序:先乘方,再乘除,然后加减,最后结果分子、分母要进行约分,注意运算的结果要是最简分式.
例5、计算(1)
[分析] 这道题先做括号里的减法,再把除法转化成乘法,把分母的“-”号提到分式本身的前边..
解:
=
练习:(1) ; (2)
(3) ; (4) ;
(5) (6)
(7) (8)
思考题:(1)已知:3a=4b. 求分式的值。
(2)化简:
作业:1、计算
(1) (2)
(3) (4):÷
2.计算,并求出当-1的值.
中考试题中的分式内容:
1、(2003.南宁)计算:÷
2、(2004.安徽)计算:
3、(2005,河北)已知,求÷的值。
4、化简:
7. 某哨所运来一筐苹果,共有60个,计划每名战士分若干个,还多5个;若每名战士多分1个,则差6个.求共有多少名战士
8. 某商店甲种糖果的单价为每千克20元,乙种糖果的单价为每千克16元.为了促销,现将10千克乙种糖果和一包甲种糖果混合(搅匀)销售,如果将混合后的糖果单价定为每千克17.5元,那么混合销售与分开销售的销售额相同.这包甲种糖果有多少千克
9. 某商厦进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市后果然供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了4元.商厦销售这种衬衫时每件定价都是58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商厦共赢利多少元
10. 某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
(1)你能找出这一情境中的等量关系吗?
(2)根据这一情境你能提出哪些问题 (3)你能利用方程求出这两年每间房屋的租金各是多少吗
11.甲、乙两班学生参加植树劳动,已知甲班学生每天比乙班学生多种5棵树,甲班种80棵树所用的天数与乙班种70棵树所用的天数相等.求甲班学生每天种多少棵树.
12.某市为了缓解市区的交通拥堵,更好地方便市民乘坐公交车,决定在市区主干道修建一条公交车专用车道,为了使工程提前3天完成,需要将原订的工作效率提高12%,求原计划完成这项工程需用多少天?
13.为了方便广西游客到昆明参观游览“世博会”,铁路部门临时增开了一列南宁—昆明的直达快车.已知南宁、昆明两地相距828km,假如一列直达快车和一列普通快车都由南宁开往昆明,普通快车先出发2h,结果比直达快车晚到4h,若直达快车速度是普通快车的1.5倍,求普通快车的速度.
14.某公司招聘打字员,要求每分钟至少打45个字.已知应聘者乙的工作效率比甲高25%,而甲打1800字的时间比乙打2000字的时间多5分钟.问甲、乙两人的打字速度是否能达到公司的要求.
15.比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴出发,到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.
16.联系实际编拟一道关于分式方程-=的应用题,要求表述完整,条件充分并写出解答过程.
PAGE
1
1、知道负整数指数幂=(a≠0,n是正整数).
2、掌握整数指数幂的运算性质.
3、会用科学计数法表示小于1的数.
4、明确分式混合运算的顺序,熟练地进行分式的混合运算
一、整数指数幂的运算性质:
(1)同底数的幂的乘法:(m,n是整数,当m或n为负整数时,);
(2)幂的乘方:(m,n是整数,当m或n为负整数时,);
(3)积的乘方:(n是整数,当n为负整数时,,);
(4)同底数的幂的除法:( a≠0,m ,n是整数);
(5)商的乘方:(n是整数,,n为负整数时,);
例1:计算 (1) (2)
(3) (3×10-8)×(4×103) (4) (2×10-3)2÷(10-3)3
1.填空
(1)-22= (2)(-2)2= (3)(-2) 0=
(4)20= ( 5)2 -3= ( 6)(-2) -3=
(7) (8) ()
例2、下列等式是否正确?为什么?
(1) (2)
例3、纳米是非常小的长度单位,1纳米=米,把1纳米的物体放到乒乓球上,就如同把乒乓球放到地球上.1立方毫米的空间可以放多少个1立方纳米的物体?
例4、计算
[分析] 这道题是分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序:先乘方,再乘除,然后加减,最后结果分子、分母要进行约分,注意运算的结果要是最简分式.
例5、计算(1)
[分析] 这道题先做括号里的减法,再把除法转化成乘法,把分母的“-”号提到分式本身的前边..
解:
=
练习:(1) ; (2)
(3) ; (4) ;
(5) (6)
(7) (8)
思考题:(1)已知:3a=4b. 求分式的值。
(2)化简:
作业:1、计算
(1) (2)
(3) (4):÷
2.计算,并求出当-1的值.
中考试题中的分式内容:
1、(2003.南宁)计算:÷
2、(2004.安徽)计算:
3、(2005,河北)已知,求÷的值。
4、化简:
7. 某哨所运来一筐苹果,共有60个,计划每名战士分若干个,还多5个;若每名战士多分1个,则差6个.求共有多少名战士
8. 某商店甲种糖果的单价为每千克20元,乙种糖果的单价为每千克16元.为了促销,现将10千克乙种糖果和一包甲种糖果混合(搅匀)销售,如果将混合后的糖果单价定为每千克17.5元,那么混合销售与分开销售的销售额相同.这包甲种糖果有多少千克
9. 某商厦进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市后果然供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了4元.商厦销售这种衬衫时每件定价都是58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商厦共赢利多少元
10. 某单位将沿街的一部分房屋出租.每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
(1)你能找出这一情境中的等量关系吗?
(2)根据这一情境你能提出哪些问题 (3)你能利用方程求出这两年每间房屋的租金各是多少吗
11.甲、乙两班学生参加植树劳动,已知甲班学生每天比乙班学生多种5棵树,甲班种80棵树所用的天数与乙班种70棵树所用的天数相等.求甲班学生每天种多少棵树.
12.某市为了缓解市区的交通拥堵,更好地方便市民乘坐公交车,决定在市区主干道修建一条公交车专用车道,为了使工程提前3天完成,需要将原订的工作效率提高12%,求原计划完成这项工程需用多少天?
13.为了方便广西游客到昆明参观游览“世博会”,铁路部门临时增开了一列南宁—昆明的直达快车.已知南宁、昆明两地相距828km,假如一列直达快车和一列普通快车都由南宁开往昆明,普通快车先出发2h,结果比直达快车晚到4h,若直达快车速度是普通快车的1.5倍,求普通快车的速度.
14.某公司招聘打字员,要求每分钟至少打45个字.已知应聘者乙的工作效率比甲高25%,而甲打1800字的时间比乙打2000字的时间多5分钟.问甲、乙两人的打字速度是否能达到公司的要求.
15.比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴出发,到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.
16.联系实际编拟一道关于分式方程-=的应用题,要求表述完整,条件充分并写出解答过程.
PAGE
1
