2022年春安徽省各地沪科版数学七年级下册期末试题选编第10章 相交线、平行线与平移 练习题(含解析)
文档属性
| 名称 | 2022年春安徽省各地沪科版数学七年级下册期末试题选编第10章 相交线、平行线与平移 练习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览


文档简介
第10章 相交线、平行线与平移 练习题
一、单选题
1.(2022秋·安徽合肥·七年级统考期末)如图,在平面内作已知直线的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
2.(2022春·安徽阜阳·七年级统考期末)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短 B.点到直线的距离
C.两点确定一条直线 D.垂线段最短
3.(2022春·安徽池州·七年级统考期末)如图,已知三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D,则表示点A到直线CD距离的是( )
A.线段CD的长度 B.线段AC的长度 C.线段AD的长度 D.线段BC的长度
4.(2022春·安徽六安·七年级统考期末)如图所示,已知AC⊥BC于点C、CD⊥AB于点D,小丽总结出以下结论:
①线段CA、CD、CB,其中最短的线段是CD;②过点B作直线AC的垂线,可作无数条;③能表示点到直线(或线段)距离的不同线段有5条;小丽得出的结论正确的有( )个.
A.0 B.1 C.2 D.3
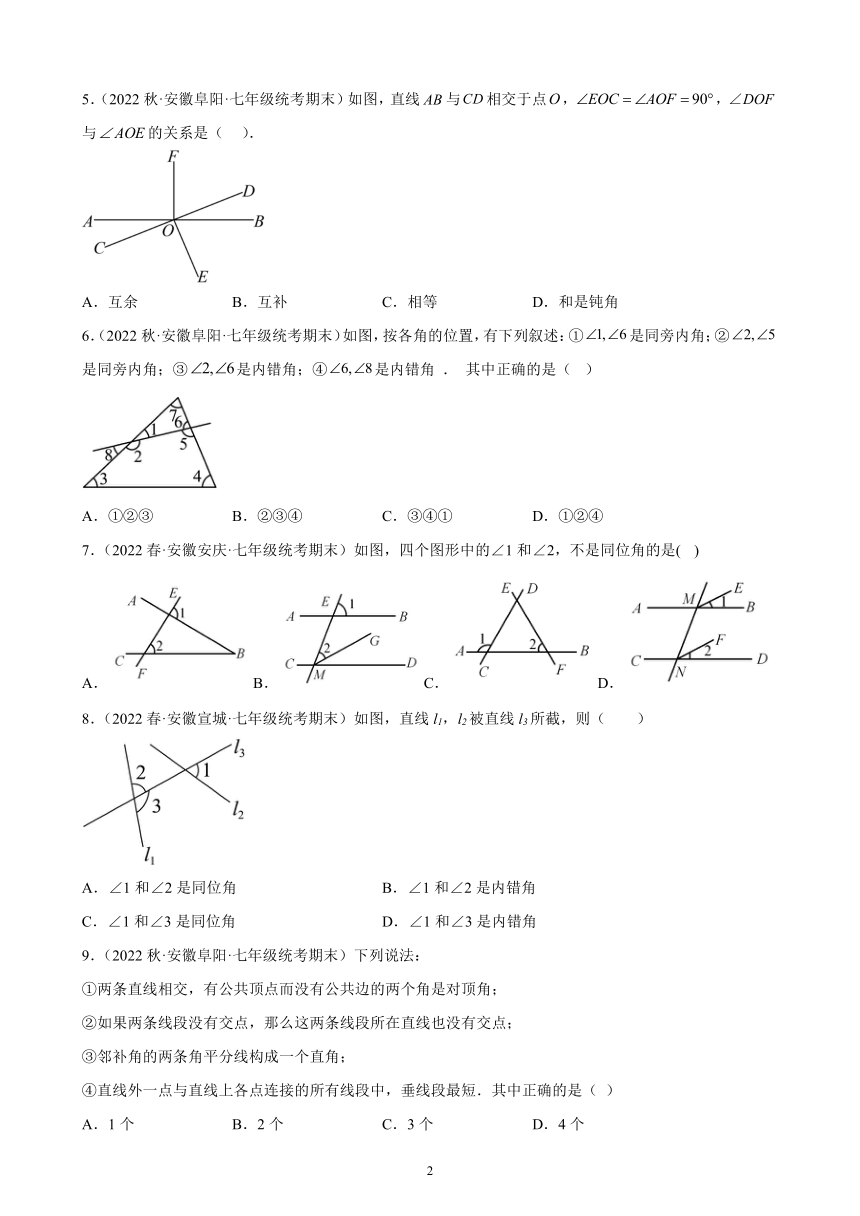
5.(2022秋·安徽阜阳·七年级统考期末)如图,直线与相交于点,,与的关系是( ).
A.互余 B.互补 C.相等 D.和是钝角
6.(2022秋·安徽阜阳·七年级统考期末)如图,按各角的位置,有下列叙述:①是同旁内角;②是同旁内角;③是内错角;④是内错角 . 其中正确的是( )
A.①②③ B.②③④ C.③④① D.①②④
7.(2022春·安徽安庆·七年级统考期末)如图,四个图形中的∠1和∠2,不是同位角的是( )
A.B.C. D.
8.(2022春·安徽宣城·七年级统考期末)如图,直线l1,l2被直线l3所截,则( )
A.∠1和∠2是同位角 B.∠1和∠2是内错角
C.∠1和∠3是同位角 D.∠1和∠3是内错角
9.(2022秋·安徽阜阳·七年级统考期末)下列说法:
①两条直线相交,有公共顶点而没有公共边的两个角是对顶角;
②如果两条线段没有交点,那么这两条线段所在直线也没有交点;
③邻补角的两条角平分线构成一个直角;
④直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
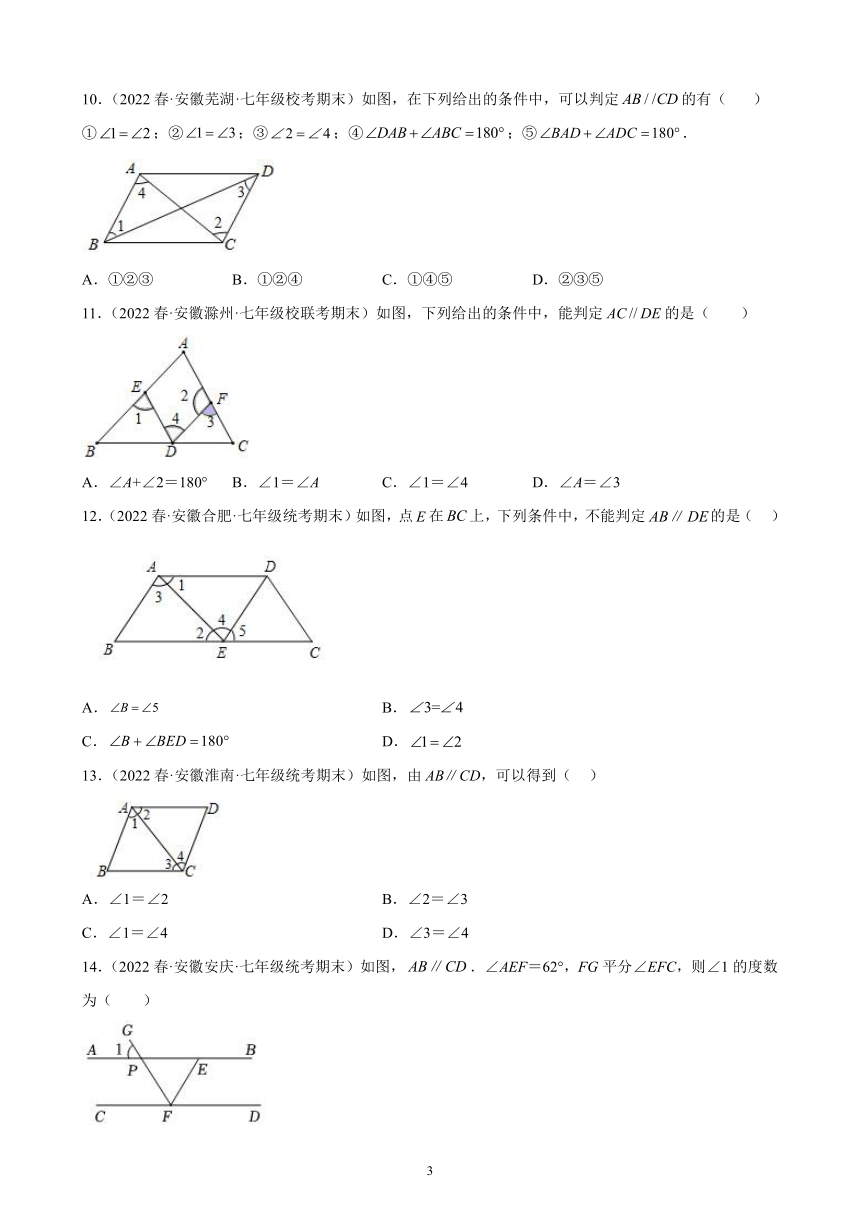
10.(2022春·安徽芜湖·七年级校考期末)如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
11.(2022春·安徽滁州·七年级校联考期末)如图,下列给出的条件中,能判定ACDE的是( )
A.∠A+∠2=180° B.∠1=∠A C.∠1=∠4 D.∠A=∠3
12.(2022春·安徽合肥·七年级统考期末)如图,点在上,下列条件中,不能判定的是( )
A. B.
C. D.
13.(2022春·安徽淮南·七年级统考期末)如图,由AB∥CD,可以得到( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
14.(2022春·安徽安庆·七年级统考期末)如图,.∠AEF=62°,FG平分∠EFC,则∠1的度数为( )
A.62° B.60° C.59° D.50°
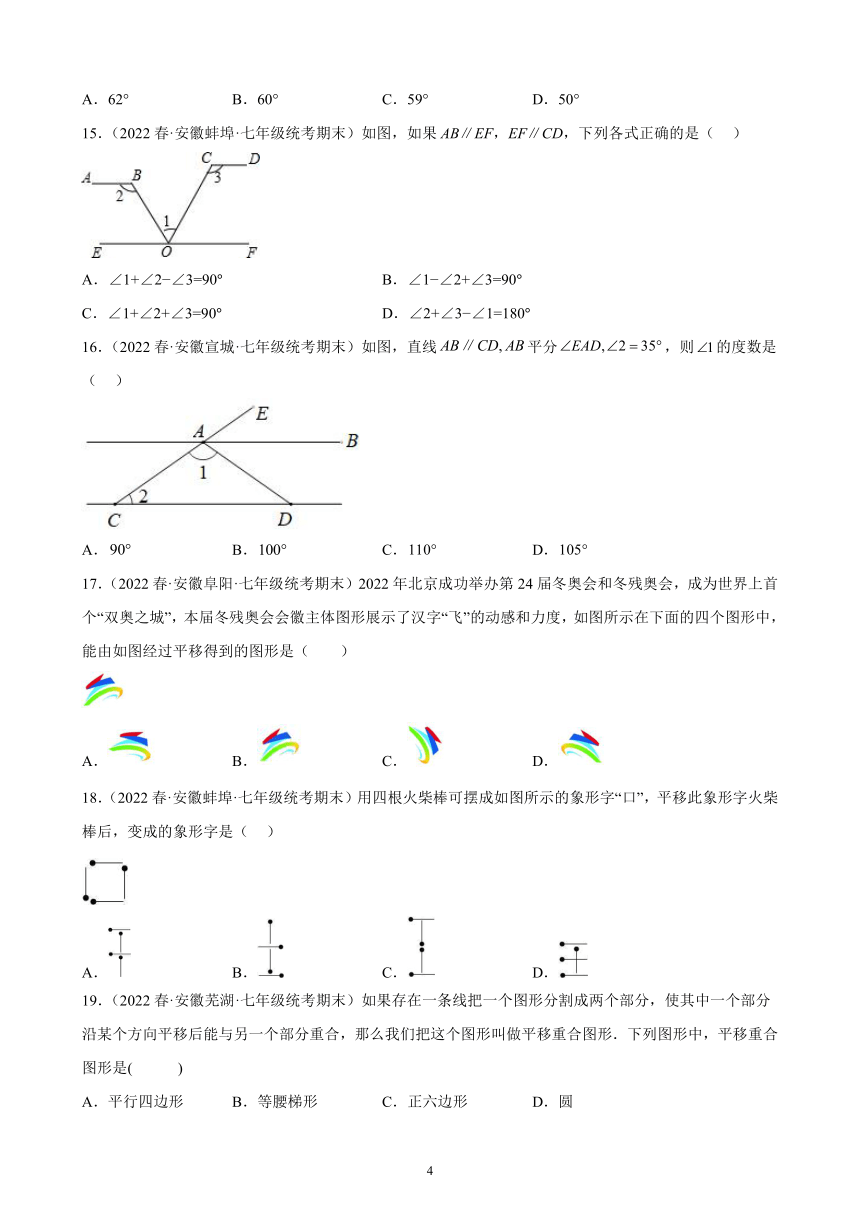
15.(2022春·安徽蚌埠·七年级统考期末)如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2 ∠3=90° B.∠1 ∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3 ∠1=180°
16.(2022春·安徽宣城·七年级统考期末)如图,直线平分,则的度数是( )
A. B. C. D.
17.(2022春·安徽阜阳·七年级统考期末)2022年北京成功举办第24届冬奥会和冬残奥会,成为世界上首个“双奥之城”,本届冬残奥会会徽主体图形展示了汉字“飞”的动感和力度,如图所示在下面的四个图形中,能由如图经过平移得到的图形是( )
A. B. C. D.
18.(2022春·安徽蚌埠·七年级统考期末)用四根火柴棒可摆成如图所示的象形字“口”,平移此象形字火柴棒后,变成的象形字是( )
A. B. C. D.
19.(2022春·安徽芜湖·七年级统考期末)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
二、填空题
20.(2022春·安徽池州·七年级统考期末)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD∶∠COM=1∶2,则∠AOD的大小为________.
21.(2022春·安徽池州·七年级统考期末)三条直线a、b、c中,若a⊥b,b∥c,则a与c的位置关系是___________.
22.(2022春·安徽阜阳·七年级统考期末)如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件:______.(只写一个即可,不添加任何字母或数字)
23.(2022春·安徽阜阳·七年级统考期末)如图,AD∥BC,BD平分∠ABC,∠A=104°,∠C:∠DBC=3:2,则∠C=_________.
24.(2022春·安徽淮南·七年级统考期末)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
三、解答题
25.(2022秋·安徽合肥·七年级统考期末)按要求画图:
(1)如图1,点是平面上的两个定点.
①连按;
②反向延长线段至,使;
(2)如图2,是的边,上的一点.
①过点画的垂线,交于点;
②过点画的垂线,垂足为.
26.(2022秋·安徽铜陵·七年级统考期末)如图,已知点A,点B,点D,点E,点F
(1)作直线BE,连接AF,线段AF与直线BE交于点C,作射线CD.
(2)在(1)所画图中,若,CD平分,求的大小.
27.(2022春·安徽安庆·七年级统考期末)如图,点是直线AB上一点,OD平分∠AOC,∠BOE=3∠COE,∠DOE=81°,求∠BOE,∠AOD的度数.
28.(2022秋·安徽淮南·七年级校联考期末)如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
29.(2022春·安徽芜湖·七年级统考期末)请将下列证明过程补充完整:
已知:如图,点P在CD上,已知,.
求证:
证明:∵(已知)
∴______//______(______)
∴______(______)
又∵(已知)
∴______
即______(等式的性质)
∴//(内错角相等,两直线平行)
∴(______)
30.(2022春·安徽安庆·七年级统考期末)如图,已知AMBN,∠A=60°,点P是射线AM上一动点与点A不重合,BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数是______.
31.(2022春·安徽芜湖·七年级校考期末)已知:如图,.
(1)求证:;
(2)求的度数.
32.(2022春·安徽宿州·七年级校考期末)如图,已知AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2.求证:∠C=∠D.
解:∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=_______( 等量代换 )
∴_______∥_______(同位角相等,两直线平行)
∴∠C=_______(两直线平行,同位角相等)
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
33.(2022春·安徽合肥·七年级统考期末)如图,在边长为1个单位长度的小正方形组成的网格中,的顶点A、B、C在小正方形的顶点上,将向右平移4单位,再向上平移4个单位得到.
(1)在网格中画出.
(2)的面积为__________.
(3)线段与线段的关系为___________.
34.(2022春·安徽滁州·七年级校考期末)已知,AD//BC,∠A=∠C=120°,试回答下列问题:
(1)如图①,求证:AB//DC;
(2)如图②,若点E、F在线段AD上,且满足∠FBD=∠CBD,并且BE平分∠ABF,求∠EBD的度数;
(3)在(2)的条件下,如果平行移动DC的过程中,当∠BEA=∠BDC时,求此时∠BDC的度数.
35.(2022春·安徽宣城·七年级统考期末)如图是由相同边长的小正方形组成的网格图形,每个小正方形的边长为1个单位长度,每个小正方形的顶点都叫做格点,三角形的三个顶点都在格点上,利用网格画图。
(1)画出三角形ABC向右平移8个单位长度后三角形的位置;
(2)过点A画BC的平行线,并标出平行线所过格点Q;
(3)三角形的面积为_______.
参考答案:
1.D
【分析】在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.
【详解】在同一平面内,画已知直线的垂线,可以画无数条;
故选:D.
【点睛】此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.
2.D
【分析】根据垂线段的性质:垂线段最短进行解答.
【详解】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,
故选:D.
【点睛】本题考查垂线段的性质:垂线段最短,熟练掌握垂线段的定义是解题的关键.
3.C
【分析】根据点到直线的距离的概念:直线外一点到这条直线的垂线段的长度即为该点到这条直线的距离作答即可.
【详解】解:点A到CD的距离是线段AD的长度.
故选C.
【点睛】本题主要考查了点到直线的距离的概念,解题的关键是熟练掌握并理解点到直线的距离的概念.
4.C
【分析】根据点到直线的距离垂线段最短即可判断①;根据垂线的定义即可判断②③.
【详解】解:∵点到直线的距离垂线段最短,CD⊥AB,
∴线段CA、CD、CB,其中最短的线段是CD,故①正确;
过点B作直线AC的垂线只能作一条,故②错误;
∵AC表示A到BC的距离,BC表示B到AC的距离,CD表示C到AD、C到BD,C到AB的距离,
∴能表示点到直线(或线段)距离的不同线段有5条,故③正确;
故选C.
【点睛】本题主要考查了点到直线(线段)的距离,垂线段最短,熟知相关知识是解题的关键.
5.B
【分析】由已知条件可得,再根据可得出,,可推出.
【详解】解:∵直线与相交于点,
∴(对顶角相等),
∵,
∴,
∵,
∴.
∴与的关系是互补.
故选:B.
【点睛】本题考查的知识点是对顶角以及邻补角,掌握对顶角以及邻补角的定义是解此题的关键.
6.A
【分析】根据同旁内角,内错角的定义,逐项判断即可求解.
【详解】解:①是同旁内角,正确;
②是同旁内角,正确;
③是内错角,正确;
④不是内错角 ,故原说法错误.
所以正确的是①②③.
故选:A
【点睛】本题主要考查了同位角,内错角,同旁内角的定义,熟练掌握两条直线被第三条直线所截,在截线的同旁、被截两直线的同一方,我们把这种位置关系的角称为同位角;两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;两条直线被第三条直线所截,在两条被截线之间,并在截线同旁的两个角称为同旁内角是解题的关键.
7.D
【分析】要想成为同位角,两个角必须有一对边在同一条直线上,依据这一条件分析判断即可.
【详解】A、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
C、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
D、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
D、∠1、∠2的两条边都不在一条直线上,不是同位角;
故选:D
【点睛】本题考查同位角的定义,解题的关键是熟悉三线八角的位置关系.
8.C
【分析】两条直线a、b被第三条直线c所截,在截线c的同旁,被截两直线a、b的同一侧的角(都在左侧或者都在右侧),把这样的两个角称为同位角;根据定义分别判断即可.
【详解】解:∠1和∠2既不是同位角,也不是内错角,故选项A、B错误;
∠1和∠3是同位角,故选项C正确,选项D错误;
故答案为:C.
【点睛】本题考查了同位角、内错角、同旁内角,掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形是解题的关键.
9.C
【分析】根据相关定义对各选项逐一进行判定,即可得出结论.
【详解】解:①两条直线相交,有公共顶点而没有公共边的两个角是对顶角,对;
②直线延长可能有交点,错;
③邻补角的两条角平分线构成一个直角,对;
④直线外一点与直线上各点连接的所有线段中,垂线段最短,对.
故选C.
【点睛】本题考查了垂线段最短、对顶角以及邻补角,熟练掌握,直线外一点与直线上各点连接的所有线段中,垂线段最短以及对顶角的定义是解题的关键.
10.D
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
【详解】解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
【点睛】本题考查了平行线的判定,正确掌握平行线的判定方法是解题的关键.
11.B
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
【详解】解:A选项:∵∠A+∠2=180°,同旁内角互补,两直线平行,∴ABDF,不符合题意;
B选项:∵∠1=∠A,同位角相等,两直线平行,∴ACDE,符合题意;
C选项:∵∠1=∠4,内错角相等,两直线平行,∴ABDF,不符合题意;
D选项:∵∠A=∠3,同位角相等,两直线平行,∴ABDF,不符合题意,
故选:B.
【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键,①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.
12.D
【分析】根据平行线的判定定理判断求解即可.
【详解】解:∵∠B=∠5,
∴,故A选项不符合题意;
∵∠3=∠4,
∴,故B选项不符合题意;
∵∠B+∠BED=180°,
∴,故C选项不符合题意;
∵∠l=∠2,
∴ADBC,故D选项符合题意;
故选:D.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
13.C
【分析】根据平行线的性质解答即可.
【详解】解:A、与不是两平行线、形成的角,故错误,不符合题意;
B、与不是两平行线、形成的内错角,故错误,不符合题意;
C、与是两平行线、形成的内错角,故正确,符合题意;
D、与不是两平行线、形成的角,无法判断两角的数量关系,故错误,不符合题意;
故选:C.
【点睛】本题考查了平行线的性质,解题的关键是注意和的位置关系.
14.C
【分析】根据“两直线平行,同旁内角互补”,求出,根据“两直线平行,同位角相等”,求出;
【详解】解:∵,
∴,
∵,
∴,
∵FG平分∠EFC,
∴ ,
∵,
∴,
故选:C.
【点睛】本题考查平行线的性质:“两直线平行,同旁内角互补” ,“两直线平行,同位角相等”,熟记相关性质是解题关键.
15.D
【分析】根据平行线的性质,即可得到∠3=∠COE,∠2+∠BOE=180°,进而得出∠2+∠3-∠1=180°.
【详解】∵EFCD,
∴∠3=∠COE,
∴∠3 ∠1=∠COE ∠1=∠BOE,
∵ABEF,
∴∠2+∠BOE=180°,即∠2+∠3 ∠1=180°.
故选:D.
【点睛】本题考查了平行线的性质,两条直线平行,内错角相等;两直线平行,同旁内角互补.
16.C
【分析】根据邻补角的定义、角平分线的定义及平行线的性质求解即可.
【详解】解:∵AB∥CD,∠2=35°,
∴∠EAB=∠2 =35°,
∵AB平分∠EAD,
∴∠EAD=2∠EAB=70°,
∵∠1+∠EAD=180°,
∴∠1 =180°-∠EAD =180°-70°=110°,
故选:C.
【点睛】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
17.B
【分析】根据平移的性质,即可判断.
【详解】解:如图所示在上面的四个图形中,能由如图经过平移得到的图形是:B,
故选:B.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
18.C
【分析】由平移的性质,结合图形,采用排除法判断正确结果.
【详解】解:原图形平移后,水平的火柴头应在左边,竖直的火柴头应是一上一下.只有C符合.
故选:C.
【点睛】本题利用了平移的基本性质:平移不改变图形的形状、大小和方向,只改变图形的位置.
19.A
【分析】证明平行四边形是平移重合图形即可.
【详解】如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
则有:AF=FD,BE=EC,AB=EF=CD,
∴四边形ABEF向右平移可以与四边形EFCD重合,
∴平行四边形ABCD是平移重合图形.
故选:A.
【点睛】本题考查平移的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
20.150°##150度
【分析】先根据OM⊥AB,得∠BOM = 90°,再∠BOD:∠COM = 1: 2,可求出∠DOB再根据平角关系,即可得出∠AOD的度数.
【详解】∵∠BOD:∠COM=1:2,
∴∠COM = 2∠BOD
∵∠BOD=∠AOC
∴∠COM =2∠AOC
又∠AOM=∠COM+∠AOC,
=2∠AOC +∠AOC= 3∠AOC,
∵OM⊥AB,
∴∠AOM = 90°,
∠AOC=∠AOM=90°=30°,
∠AOD= 180°-∠AOC= 180°- 30°= 150°,
故答案为: 150°
【点睛】本题考查了垂线的定义及角的计算,垂线,对顶角、邻补角,解决本题的关键是利用角之间的和与差进行解答.
21.a⊥c(或垂直)
【分析】根据平行公理以及垂直的意义的判断推论即可.
【详解】解:∵三条直线a、b、c中,a⊥b,b∥c,
∴a⊥c,
故答案是:a⊥c(或垂直).
【点睛】本题考查的是平行公理的推论,掌握平行的定义和垂直的意义是解题的关键.
22.或或
【分析】根据平行线的判定定理即可写出.
【详解】解:当或或时,,
故答案为:或或.
【点睛】本题考查了平行线的判定,熟练掌握和运用平行线的判定定理是解决本题的关键.
23.57°##57度
【分析】根据,,得出,根据平分,得出,最后根据得出的度数即可.
【详解】解:,
,
,
,
平分,
,
,
.
故答案为:57°.
【点睛】本题主要考查了平行线的性质,角平分线的定义,熟练掌握两直线平行同旁内角互补是解题的关键.
24.120
【分析】先过点B作BF//CD,由CD//AE,可得CD//BF//AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
【详解】解:如图,过点B作BF//CD,
∵CD//AE,
∴CD//BF//AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=150°,∠BAE=90°,
∴∠1=30°,∠2=90°,
∴∠ABC=∠1+∠2=120°.
故答案为:120.
【点睛】此题考查了平行线的性质,解题的关键是注意掌握辅助线的作法,注意数形结合思想的应用.
25.(1)见解析
(2)见解析
【分析】(1)根据线段的作法连接MN即可,再延长NM,截取MN=DM即可;
(2)根据过直线上一点作垂线的方法,得出即可.
(1)
如图所示:
(2)
如图所示:
【点睛】此题主要考查了复杂作图,熟练掌握基本作图方法是解题关键.
26.(1)答案见解析;(2).
【分析】(1)根据直线是向两方无限延伸的画直线BE,根据线段不能向任何一方延伸,画线段AF,根据射线是向一方无限延伸的画射线CD;
(2)先根据补角的定义可求出,再根据角平分线的性质求出,则答案即可解得.
【详解】解:(1)如图所示:
(2)∵,
∴,
又∵CD平分,
∴,
∴.
【点睛】本题主要考查了邻补角的定义,直线、射线和线段,关键是掌握直线向两方无限延伸,射线向一方无限延伸,线段不能向任何一方延伸.
27.∠BOE=27°,∠AOD=72°.
【分析】设∠COE=x,则∠AOD=81°-x,则∠BOE=3x,∠AOC=2 ∠AOD,由∠AOC+∠BOC=180° ,列方程2+4x=180°,解方程求解即可.
【详解】解:设∠COE=x,
∵∠BOE=3∠COE,OD平分∠AOC,∠DOE
∠BOE=3∠COE,则∠BOE=3x,∠AOC=2,
∵O是直线AB上一点,
∴ ∠AOC+∠BOC=180° ,
∴2+4x=180°,
解得
∠AOD=81°-
∴∠BOE=27°,∠AOD= 72°.
【点睛】本题考查的是角平分线的定义,角的和差运算,邻补角的含义,解本题的关键是运用方程的思想解决几何问题.
28.(1)
(2)
【分析】(1)由角平分线的定义可求出,再根据对顶角相等即可求解;
(2)设,则,根据,可列出关于x的方程,解出x的值,即可求出的大小,再根据(1)同理即可求出的大小.
【详解】(1)平分,
,
;
(2)设,则,
根据题意得,
解得,
,
,
.
【点睛】本题考查角平分线的定义,邻补角的定义.利用数形结合的思想是解题关键.
29.AB;CD;同旁内角互补,两直线平行;∠APC;两直线平行,内错角相等;∠1;∠APC;∠4;内错角相等,两直线平行;两直线平行,内错角相等.
【分析】根据平行线的性质和判定即可解决问题.
【详解】证明:∵(已知)
∴(同旁内角互补,两直线平行)
∴(两直线平行,内错角相等)
又∵(已知)
∴
即(等式的性质)
∴(内错角相等,两直线平行)
∴(两直线平行,内错角相等);
故答案为:AB;CD;同旁内角互补,两直线平行;∠APC;两直线平行,内错角相等;∠1;∠APC;∠4;内错角相等,两直线平行;两直线平行,内错角相等.
【点睛】本题考查平行线的性质和判定,熟练掌握平行线的判定定理和性质定理是解决问题的关键.
30.(1)∠CBD=60°;
(2)不变,∠APB=2∠ADB,理由见解析;
(3)30°.
【分析】(1)根据平行线的性质求出∠ABN=120°,再根据角平分线的定义求解即可;
(2)不变,根据平行线的性质求出∠APB=∠PBN,∠ADB=∠DBN,然后根据角平分线的定义求出∠ADB=∠DBN=∠PBN=∠APB,即可得出结论;
(3)根据平行线的性质求出∠ACB=∠CBN,结合已知可得∠CBN=∠ABD,然后证明∠ABC=∠CBP=∠DBP=∠DBN即可解决问题.
【详解】(1)解:∵AMBN,
∴∠ABN=180° ∠A=120°,
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°;
(2)不变,∠APB=2∠ADB,
理由:∵AMBN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,
∴∠APB=2∠ADB;
(3)∵AMBN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD ∠CBD,∠DBN=∠CBN ∠CBD,
∴∠ABC=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为:30°.
【点睛】本题考查了平行线的性质、角平分线的定义等知识,解题的关键是熟练掌握相关性质定理并能灵活运用.
31.(1)证明见解析
(2)∠C=
【分析】(1)先证明,可得FGB,再证明,从而可得答案;
(2)由,可得,再把 代入进行计算即可.
【详解】(1)证明:,
∴,
FGB,
,
,
∴;
(2)解:由(1)得,,
,
,
∴=
,
.
【点睛】本题考查的是平行线的判定与性质,方程思想的应用,掌握“平行线的判定与性质”是解本题的关键.
32.对顶角相等 ,∠DGH, BD∥CE ,∠ABG, 已知,两直线平行,内错角相等,等量代换,
【详解】证明:∵∠1=∠2(已知)
∠1=∠DGH(对顶角相等),
∴∠2=∠DGH(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABG(两直线平行,同位角相等)
又∵AC∥DF(已知)
∴∠D=∠ABG(两直线平行,内错角相等)
∴∠C=∠D(等量代换).
33.(1)见解析
(2)
(3)
【分析】(1)根据题意进行平移作图即可;
(2)根据三角形的面积公式求解即可;
(3)根据平移的性质即可得出答案.
(1)
如图,即为所求;
(2)
由题意得,,
故答案为:;
(3)
平移,
,
故答案为:.
【点睛】本题考查了平移作图,三角形的面积公式及平移的性质,熟练掌握平移不改变图形的形状和大小是解题的关键.
34.(1)证明见解析
(2)∠EBD=30°
(3)∠BDC=45°
【分析】(1)证明∠C+∠B=180°即可;
(2)证明∠EBF+∠FBD=∠ABC即可得到结论;
(3)证明∠ABE=∠EBF=∠FBD=∠CBD=15°即可得到结论.
(1)
∵AD//BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB//DC.
(2)
∵∠A+∠ABC=180°,∠A=120°,
∴∠ABC=60°,
∵BE平分∠ABF,
∴∠EBF=∠ABF,
∵∠FBD=∠CBD,
∴∠FBD=∠FBC,
∴∠EBF+∠FBD=(∠ABF+∠FBC)
=∠ABC=30°,
∴∠EBD=30°.
(3)
∵AD//BC,
∴∠BEA=∠EBC,
∵AB∥DC,
∴∠BDC=∠ABD,
∵∠BEA=∠BDC,
∴∠EBC=∠ABD,
∴∠CBD+∠EBD=∠ABE+∠EBD,
∴∠CBD=∠ABE,
∵∠ABE=∠EBF,∠FBD=∠CBD,
∴∠ABE=∠EBF=∠FBD=∠CBD,
∵∠ABC=60°,
∴∠ABE=∠EBF=∠FBD=∠CBD=15°,
∴∠ABD=45°,
∴∠BDC=∠ABD=45°.
【点睛】本题考查平移和平行线的性质的有关知识.平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
35.(1)见解析
(2)见解析
(3)
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A′,B′,C′即可;
(2)根据平行线的定义和网格特点画出图形即可;
(3)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(1)
如图,
(2)
如图,
(3)
三角形A′B′C′的面积= .
故答案为:.
【点睛】本题主要考查了平移的性质,网格中平行线的画法,三角形的面积等知识,明确网格中画平行线的方法是解题的关键.
一、单选题
1.(2022秋·安徽合肥·七年级统考期末)如图,在平面内作已知直线的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
2.(2022春·安徽阜阳·七年级统考期末)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短 B.点到直线的距离
C.两点确定一条直线 D.垂线段最短
3.(2022春·安徽池州·七年级统考期末)如图,已知三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D,则表示点A到直线CD距离的是( )
A.线段CD的长度 B.线段AC的长度 C.线段AD的长度 D.线段BC的长度
4.(2022春·安徽六安·七年级统考期末)如图所示,已知AC⊥BC于点C、CD⊥AB于点D,小丽总结出以下结论:
①线段CA、CD、CB,其中最短的线段是CD;②过点B作直线AC的垂线,可作无数条;③能表示点到直线(或线段)距离的不同线段有5条;小丽得出的结论正确的有( )个.
A.0 B.1 C.2 D.3
5.(2022秋·安徽阜阳·七年级统考期末)如图,直线与相交于点,,与的关系是( ).
A.互余 B.互补 C.相等 D.和是钝角
6.(2022秋·安徽阜阳·七年级统考期末)如图,按各角的位置,有下列叙述:①是同旁内角;②是同旁内角;③是内错角;④是内错角 . 其中正确的是( )
A.①②③ B.②③④ C.③④① D.①②④
7.(2022春·安徽安庆·七年级统考期末)如图,四个图形中的∠1和∠2,不是同位角的是( )
A.B.C. D.
8.(2022春·安徽宣城·七年级统考期末)如图,直线l1,l2被直线l3所截,则( )
A.∠1和∠2是同位角 B.∠1和∠2是内错角
C.∠1和∠3是同位角 D.∠1和∠3是内错角
9.(2022秋·安徽阜阳·七年级统考期末)下列说法:
①两条直线相交,有公共顶点而没有公共边的两个角是对顶角;
②如果两条线段没有交点,那么这两条线段所在直线也没有交点;
③邻补角的两条角平分线构成一个直角;
④直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
10.(2022春·安徽芜湖·七年级校考期末)如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
11.(2022春·安徽滁州·七年级校联考期末)如图,下列给出的条件中,能判定ACDE的是( )
A.∠A+∠2=180° B.∠1=∠A C.∠1=∠4 D.∠A=∠3
12.(2022春·安徽合肥·七年级统考期末)如图,点在上,下列条件中,不能判定的是( )
A. B.
C. D.
13.(2022春·安徽淮南·七年级统考期末)如图,由AB∥CD,可以得到( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
14.(2022春·安徽安庆·七年级统考期末)如图,.∠AEF=62°,FG平分∠EFC,则∠1的度数为( )
A.62° B.60° C.59° D.50°
15.(2022春·安徽蚌埠·七年级统考期末)如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2 ∠3=90° B.∠1 ∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3 ∠1=180°
16.(2022春·安徽宣城·七年级统考期末)如图,直线平分,则的度数是( )
A. B. C. D.
17.(2022春·安徽阜阳·七年级统考期末)2022年北京成功举办第24届冬奥会和冬残奥会,成为世界上首个“双奥之城”,本届冬残奥会会徽主体图形展示了汉字“飞”的动感和力度,如图所示在下面的四个图形中,能由如图经过平移得到的图形是( )
A. B. C. D.
18.(2022春·安徽蚌埠·七年级统考期末)用四根火柴棒可摆成如图所示的象形字“口”,平移此象形字火柴棒后,变成的象形字是( )
A. B. C. D.
19.(2022春·安徽芜湖·七年级统考期末)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
二、填空题
20.(2022春·安徽池州·七年级统考期末)如图,直线AB和CD相交于O点,OM⊥AB,∠BOD∶∠COM=1∶2,则∠AOD的大小为________.
21.(2022春·安徽池州·七年级统考期末)三条直线a、b、c中,若a⊥b,b∥c,则a与c的位置关系是___________.
22.(2022春·安徽阜阳·七年级统考期末)如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件:______.(只写一个即可,不添加任何字母或数字)
23.(2022春·安徽阜阳·七年级统考期末)如图,AD∥BC,BD平分∠ABC,∠A=104°,∠C:∠DBC=3:2,则∠C=_________.
24.(2022春·安徽淮南·七年级统考期末)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=_____度.
三、解答题
25.(2022秋·安徽合肥·七年级统考期末)按要求画图:
(1)如图1,点是平面上的两个定点.
①连按;
②反向延长线段至,使;
(2)如图2,是的边,上的一点.
①过点画的垂线,交于点;
②过点画的垂线,垂足为.
26.(2022秋·安徽铜陵·七年级统考期末)如图,已知点A,点B,点D,点E,点F
(1)作直线BE,连接AF,线段AF与直线BE交于点C,作射线CD.
(2)在(1)所画图中,若,CD平分,求的大小.
27.(2022春·安徽安庆·七年级统考期末)如图,点是直线AB上一点,OD平分∠AOC,∠BOE=3∠COE,∠DOE=81°,求∠BOE,∠AOD的度数.
28.(2022秋·安徽淮南·七年级校联考期末)如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
29.(2022春·安徽芜湖·七年级统考期末)请将下列证明过程补充完整:
已知:如图,点P在CD上,已知,.
求证:
证明:∵(已知)
∴______//______(______)
∴______(______)
又∵(已知)
∴______
即______(等式的性质)
∴//(内错角相等,两直线平行)
∴(______)
30.(2022春·安徽安庆·七年级统考期末)如图,已知AMBN,∠A=60°,点P是射线AM上一动点与点A不重合,BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数是______.
31.(2022春·安徽芜湖·七年级校考期末)已知:如图,.
(1)求证:;
(2)求的度数.
32.(2022春·安徽宿州·七年级校考期末)如图,已知AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2.求证:∠C=∠D.
解:∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=_______( 等量代换 )
∴_______∥_______(同位角相等,两直线平行)
∴∠C=_______(两直线平行,同位角相等)
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
33.(2022春·安徽合肥·七年级统考期末)如图,在边长为1个单位长度的小正方形组成的网格中,的顶点A、B、C在小正方形的顶点上,将向右平移4单位,再向上平移4个单位得到.
(1)在网格中画出.
(2)的面积为__________.
(3)线段与线段的关系为___________.
34.(2022春·安徽滁州·七年级校考期末)已知,AD//BC,∠A=∠C=120°,试回答下列问题:
(1)如图①,求证:AB//DC;
(2)如图②,若点E、F在线段AD上,且满足∠FBD=∠CBD,并且BE平分∠ABF,求∠EBD的度数;
(3)在(2)的条件下,如果平行移动DC的过程中,当∠BEA=∠BDC时,求此时∠BDC的度数.
35.(2022春·安徽宣城·七年级统考期末)如图是由相同边长的小正方形组成的网格图形,每个小正方形的边长为1个单位长度,每个小正方形的顶点都叫做格点,三角形的三个顶点都在格点上,利用网格画图。
(1)画出三角形ABC向右平移8个单位长度后三角形的位置;
(2)过点A画BC的平行线,并标出平行线所过格点Q;
(3)三角形的面积为_______.
参考答案:
1.D
【分析】在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.
【详解】在同一平面内,画已知直线的垂线,可以画无数条;
故选:D.
【点睛】此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.
2.D
【分析】根据垂线段的性质:垂线段最短进行解答.
【详解】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,
故选:D.
【点睛】本题考查垂线段的性质:垂线段最短,熟练掌握垂线段的定义是解题的关键.
3.C
【分析】根据点到直线的距离的概念:直线外一点到这条直线的垂线段的长度即为该点到这条直线的距离作答即可.
【详解】解:点A到CD的距离是线段AD的长度.
故选C.
【点睛】本题主要考查了点到直线的距离的概念,解题的关键是熟练掌握并理解点到直线的距离的概念.
4.C
【分析】根据点到直线的距离垂线段最短即可判断①;根据垂线的定义即可判断②③.
【详解】解:∵点到直线的距离垂线段最短,CD⊥AB,
∴线段CA、CD、CB,其中最短的线段是CD,故①正确;
过点B作直线AC的垂线只能作一条,故②错误;
∵AC表示A到BC的距离,BC表示B到AC的距离,CD表示C到AD、C到BD,C到AB的距离,
∴能表示点到直线(或线段)距离的不同线段有5条,故③正确;
故选C.
【点睛】本题主要考查了点到直线(线段)的距离,垂线段最短,熟知相关知识是解题的关键.
5.B
【分析】由已知条件可得,再根据可得出,,可推出.
【详解】解:∵直线与相交于点,
∴(对顶角相等),
∵,
∴,
∵,
∴.
∴与的关系是互补.
故选:B.
【点睛】本题考查的知识点是对顶角以及邻补角,掌握对顶角以及邻补角的定义是解此题的关键.
6.A
【分析】根据同旁内角,内错角的定义,逐项判断即可求解.
【详解】解:①是同旁内角,正确;
②是同旁内角,正确;
③是内错角,正确;
④不是内错角 ,故原说法错误.
所以正确的是①②③.
故选:A
【点睛】本题主要考查了同位角,内错角,同旁内角的定义,熟练掌握两条直线被第三条直线所截,在截线的同旁、被截两直线的同一方,我们把这种位置关系的角称为同位角;两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;两条直线被第三条直线所截,在两条被截线之间,并在截线同旁的两个角称为同旁内角是解题的关键.
7.D
【分析】要想成为同位角,两个角必须有一对边在同一条直线上,依据这一条件分析判断即可.
【详解】A、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
C、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
D、∠1、∠2有一条边在一条直线上,另一条边在被截线的同一方,是同位角;
D、∠1、∠2的两条边都不在一条直线上,不是同位角;
故选:D
【点睛】本题考查同位角的定义,解题的关键是熟悉三线八角的位置关系.
8.C
【分析】两条直线a、b被第三条直线c所截,在截线c的同旁,被截两直线a、b的同一侧的角(都在左侧或者都在右侧),把这样的两个角称为同位角;根据定义分别判断即可.
【详解】解:∠1和∠2既不是同位角,也不是内错角,故选项A、B错误;
∠1和∠3是同位角,故选项C正确,选项D错误;
故答案为:C.
【点睛】本题考查了同位角、内错角、同旁内角,掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形是解题的关键.
9.C
【分析】根据相关定义对各选项逐一进行判定,即可得出结论.
【详解】解:①两条直线相交,有公共顶点而没有公共边的两个角是对顶角,对;
②直线延长可能有交点,错;
③邻补角的两条角平分线构成一个直角,对;
④直线外一点与直线上各点连接的所有线段中,垂线段最短,对.
故选C.
【点睛】本题考查了垂线段最短、对顶角以及邻补角,熟练掌握,直线外一点与直线上各点连接的所有线段中,垂线段最短以及对顶角的定义是解题的关键.
10.D
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
【详解】解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
【点睛】本题考查了平行线的判定,正确掌握平行线的判定方法是解题的关键.
11.B
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
【详解】解:A选项:∵∠A+∠2=180°,同旁内角互补,两直线平行,∴ABDF,不符合题意;
B选项:∵∠1=∠A,同位角相等,两直线平行,∴ACDE,符合题意;
C选项:∵∠1=∠4,内错角相等,两直线平行,∴ABDF,不符合题意;
D选项:∵∠A=∠3,同位角相等,两直线平行,∴ABDF,不符合题意,
故选:B.
【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键,①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.
12.D
【分析】根据平行线的判定定理判断求解即可.
【详解】解:∵∠B=∠5,
∴,故A选项不符合题意;
∵∠3=∠4,
∴,故B选项不符合题意;
∵∠B+∠BED=180°,
∴,故C选项不符合题意;
∵∠l=∠2,
∴ADBC,故D选项符合题意;
故选:D.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
13.C
【分析】根据平行线的性质解答即可.
【详解】解:A、与不是两平行线、形成的角,故错误,不符合题意;
B、与不是两平行线、形成的内错角,故错误,不符合题意;
C、与是两平行线、形成的内错角,故正确,符合题意;
D、与不是两平行线、形成的角,无法判断两角的数量关系,故错误,不符合题意;
故选:C.
【点睛】本题考查了平行线的性质,解题的关键是注意和的位置关系.
14.C
【分析】根据“两直线平行,同旁内角互补”,求出,根据“两直线平行,同位角相等”,求出;
【详解】解:∵,
∴,
∵,
∴,
∵FG平分∠EFC,
∴ ,
∵,
∴,
故选:C.
【点睛】本题考查平行线的性质:“两直线平行,同旁内角互补” ,“两直线平行,同位角相等”,熟记相关性质是解题关键.
15.D
【分析】根据平行线的性质,即可得到∠3=∠COE,∠2+∠BOE=180°,进而得出∠2+∠3-∠1=180°.
【详解】∵EFCD,
∴∠3=∠COE,
∴∠3 ∠1=∠COE ∠1=∠BOE,
∵ABEF,
∴∠2+∠BOE=180°,即∠2+∠3 ∠1=180°.
故选:D.
【点睛】本题考查了平行线的性质,两条直线平行,内错角相等;两直线平行,同旁内角互补.
16.C
【分析】根据邻补角的定义、角平分线的定义及平行线的性质求解即可.
【详解】解:∵AB∥CD,∠2=35°,
∴∠EAB=∠2 =35°,
∵AB平分∠EAD,
∴∠EAD=2∠EAB=70°,
∵∠1+∠EAD=180°,
∴∠1 =180°-∠EAD =180°-70°=110°,
故选:C.
【点睛】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
17.B
【分析】根据平移的性质,即可判断.
【详解】解:如图所示在上面的四个图形中,能由如图经过平移得到的图形是:B,
故选:B.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
18.C
【分析】由平移的性质,结合图形,采用排除法判断正确结果.
【详解】解:原图形平移后,水平的火柴头应在左边,竖直的火柴头应是一上一下.只有C符合.
故选:C.
【点睛】本题利用了平移的基本性质:平移不改变图形的形状、大小和方向,只改变图形的位置.
19.A
【分析】证明平行四边形是平移重合图形即可.
【详解】如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
则有:AF=FD,BE=EC,AB=EF=CD,
∴四边形ABEF向右平移可以与四边形EFCD重合,
∴平行四边形ABCD是平移重合图形.
故选:A.
【点睛】本题考查平移的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
20.150°##150度
【分析】先根据OM⊥AB,得∠BOM = 90°,再∠BOD:∠COM = 1: 2,可求出∠DOB再根据平角关系,即可得出∠AOD的度数.
【详解】∵∠BOD:∠COM=1:2,
∴∠COM = 2∠BOD
∵∠BOD=∠AOC
∴∠COM =2∠AOC
又∠AOM=∠COM+∠AOC,
=2∠AOC +∠AOC= 3∠AOC,
∵OM⊥AB,
∴∠AOM = 90°,
∠AOC=∠AOM=90°=30°,
∠AOD= 180°-∠AOC= 180°- 30°= 150°,
故答案为: 150°
【点睛】本题考查了垂线的定义及角的计算,垂线,对顶角、邻补角,解决本题的关键是利用角之间的和与差进行解答.
21.a⊥c(或垂直)
【分析】根据平行公理以及垂直的意义的判断推论即可.
【详解】解:∵三条直线a、b、c中,a⊥b,b∥c,
∴a⊥c,
故答案是:a⊥c(或垂直).
【点睛】本题考查的是平行公理的推论,掌握平行的定义和垂直的意义是解题的关键.
22.或或
【分析】根据平行线的判定定理即可写出.
【详解】解:当或或时,,
故答案为:或或.
【点睛】本题考查了平行线的判定,熟练掌握和运用平行线的判定定理是解决本题的关键.
23.57°##57度
【分析】根据,,得出,根据平分,得出,最后根据得出的度数即可.
【详解】解:,
,
,
,
平分,
,
,
.
故答案为:57°.
【点睛】本题主要考查了平行线的性质,角平分线的定义,熟练掌握两直线平行同旁内角互补是解题的关键.
24.120
【分析】先过点B作BF//CD,由CD//AE,可得CD//BF//AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
【详解】解:如图,过点B作BF//CD,
∵CD//AE,
∴CD//BF//AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=150°,∠BAE=90°,
∴∠1=30°,∠2=90°,
∴∠ABC=∠1+∠2=120°.
故答案为:120.
【点睛】此题考查了平行线的性质,解题的关键是注意掌握辅助线的作法,注意数形结合思想的应用.
25.(1)见解析
(2)见解析
【分析】(1)根据线段的作法连接MN即可,再延长NM,截取MN=DM即可;
(2)根据过直线上一点作垂线的方法,得出即可.
(1)
如图所示:
(2)
如图所示:
【点睛】此题主要考查了复杂作图,熟练掌握基本作图方法是解题关键.
26.(1)答案见解析;(2).
【分析】(1)根据直线是向两方无限延伸的画直线BE,根据线段不能向任何一方延伸,画线段AF,根据射线是向一方无限延伸的画射线CD;
(2)先根据补角的定义可求出,再根据角平分线的性质求出,则答案即可解得.
【详解】解:(1)如图所示:
(2)∵,
∴,
又∵CD平分,
∴,
∴.
【点睛】本题主要考查了邻补角的定义,直线、射线和线段,关键是掌握直线向两方无限延伸,射线向一方无限延伸,线段不能向任何一方延伸.
27.∠BOE=27°,∠AOD=72°.
【分析】设∠COE=x,则∠AOD=81°-x,则∠BOE=3x,∠AOC=2 ∠AOD,由∠AOC+∠BOC=180° ,列方程2+4x=180°,解方程求解即可.
【详解】解:设∠COE=x,
∵∠BOE=3∠COE,OD平分∠AOC,∠DOE
∠BOE=3∠COE,则∠BOE=3x,∠AOC=2,
∵O是直线AB上一点,
∴ ∠AOC+∠BOC=180° ,
∴2+4x=180°,
解得
∠AOD=81°-
∴∠BOE=27°,∠AOD= 72°.
【点睛】本题考查的是角平分线的定义,角的和差运算,邻补角的含义,解本题的关键是运用方程的思想解决几何问题.
28.(1)
(2)
【分析】(1)由角平分线的定义可求出,再根据对顶角相等即可求解;
(2)设,则,根据,可列出关于x的方程,解出x的值,即可求出的大小,再根据(1)同理即可求出的大小.
【详解】(1)平分,
,
;
(2)设,则,
根据题意得,
解得,
,
,
.
【点睛】本题考查角平分线的定义,邻补角的定义.利用数形结合的思想是解题关键.
29.AB;CD;同旁内角互补,两直线平行;∠APC;两直线平行,内错角相等;∠1;∠APC;∠4;内错角相等,两直线平行;两直线平行,内错角相等.
【分析】根据平行线的性质和判定即可解决问题.
【详解】证明:∵(已知)
∴(同旁内角互补,两直线平行)
∴(两直线平行,内错角相等)
又∵(已知)
∴
即(等式的性质)
∴(内错角相等,两直线平行)
∴(两直线平行,内错角相等);
故答案为:AB;CD;同旁内角互补,两直线平行;∠APC;两直线平行,内错角相等;∠1;∠APC;∠4;内错角相等,两直线平行;两直线平行,内错角相等.
【点睛】本题考查平行线的性质和判定,熟练掌握平行线的判定定理和性质定理是解决问题的关键.
30.(1)∠CBD=60°;
(2)不变,∠APB=2∠ADB,理由见解析;
(3)30°.
【分析】(1)根据平行线的性质求出∠ABN=120°,再根据角平分线的定义求解即可;
(2)不变,根据平行线的性质求出∠APB=∠PBN,∠ADB=∠DBN,然后根据角平分线的定义求出∠ADB=∠DBN=∠PBN=∠APB,即可得出结论;
(3)根据平行线的性质求出∠ACB=∠CBN,结合已知可得∠CBN=∠ABD,然后证明∠ABC=∠CBP=∠DBP=∠DBN即可解决问题.
【详解】(1)解:∵AMBN,
∴∠ABN=180° ∠A=120°,
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°;
(2)不变,∠APB=2∠ADB,
理由:∵AMBN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,
∴∠APB=2∠ADB;
(3)∵AMBN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD ∠CBD,∠DBN=∠CBN ∠CBD,
∴∠ABC=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为:30°.
【点睛】本题考查了平行线的性质、角平分线的定义等知识,解题的关键是熟练掌握相关性质定理并能灵活运用.
31.(1)证明见解析
(2)∠C=
【分析】(1)先证明,可得FGB,再证明,从而可得答案;
(2)由,可得,再把 代入进行计算即可.
【详解】(1)证明:,
∴,
FGB,
,
,
∴;
(2)解:由(1)得,,
,
,
∴=
,
.
【点睛】本题考查的是平行线的判定与性质,方程思想的应用,掌握“平行线的判定与性质”是解本题的关键.
32.对顶角相等 ,∠DGH, BD∥CE ,∠ABG, 已知,两直线平行,内错角相等,等量代换,
【详解】证明:∵∠1=∠2(已知)
∠1=∠DGH(对顶角相等),
∴∠2=∠DGH(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABG(两直线平行,同位角相等)
又∵AC∥DF(已知)
∴∠D=∠ABG(两直线平行,内错角相等)
∴∠C=∠D(等量代换).
33.(1)见解析
(2)
(3)
【分析】(1)根据题意进行平移作图即可;
(2)根据三角形的面积公式求解即可;
(3)根据平移的性质即可得出答案.
(1)
如图,即为所求;
(2)
由题意得,,
故答案为:;
(3)
平移,
,
故答案为:.
【点睛】本题考查了平移作图,三角形的面积公式及平移的性质,熟练掌握平移不改变图形的形状和大小是解题的关键.
34.(1)证明见解析
(2)∠EBD=30°
(3)∠BDC=45°
【分析】(1)证明∠C+∠B=180°即可;
(2)证明∠EBF+∠FBD=∠ABC即可得到结论;
(3)证明∠ABE=∠EBF=∠FBD=∠CBD=15°即可得到结论.
(1)
∵AD//BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB//DC.
(2)
∵∠A+∠ABC=180°,∠A=120°,
∴∠ABC=60°,
∵BE平分∠ABF,
∴∠EBF=∠ABF,
∵∠FBD=∠CBD,
∴∠FBD=∠FBC,
∴∠EBF+∠FBD=(∠ABF+∠FBC)
=∠ABC=30°,
∴∠EBD=30°.
(3)
∵AD//BC,
∴∠BEA=∠EBC,
∵AB∥DC,
∴∠BDC=∠ABD,
∵∠BEA=∠BDC,
∴∠EBC=∠ABD,
∴∠CBD+∠EBD=∠ABE+∠EBD,
∴∠CBD=∠ABE,
∵∠ABE=∠EBF,∠FBD=∠CBD,
∴∠ABE=∠EBF=∠FBD=∠CBD,
∵∠ABC=60°,
∴∠ABE=∠EBF=∠FBD=∠CBD=15°,
∴∠ABD=45°,
∴∠BDC=∠ABD=45°.
【点睛】本题考查平移和平行线的性质的有关知识.平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
35.(1)见解析
(2)见解析
(3)
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A′,B′,C′即可;
(2)根据平行线的定义和网格特点画出图形即可;
(3)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(1)
如图,
(2)
如图,
(3)
三角形A′B′C′的面积= .
故答案为:.
【点睛】本题主要考查了平移的性质,网格中平行线的画法,三角形的面积等知识,明确网格中画平行线的方法是解题的关键.
