2022年春安徽省各地沪科版数学八年级下册期末试题选编第18章 勾股定理 练习题 (含解析)
文档属性
| 名称 | 2022年春安徽省各地沪科版数学八年级下册期末试题选编第18章 勾股定理 练习题 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 970.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 20:35:59 | ||
图片预览



文档简介
第18章 勾股定理 练习题
一、单选题
1.(2022春·安徽蚌埠·八年级统考期末)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
2.(2022春·安徽滁州·八年级统考期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
3.(2022春·安徽铜陵·八年级统考期末)如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,现将Rt△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( )
A.10 B.5 C.4 D.3
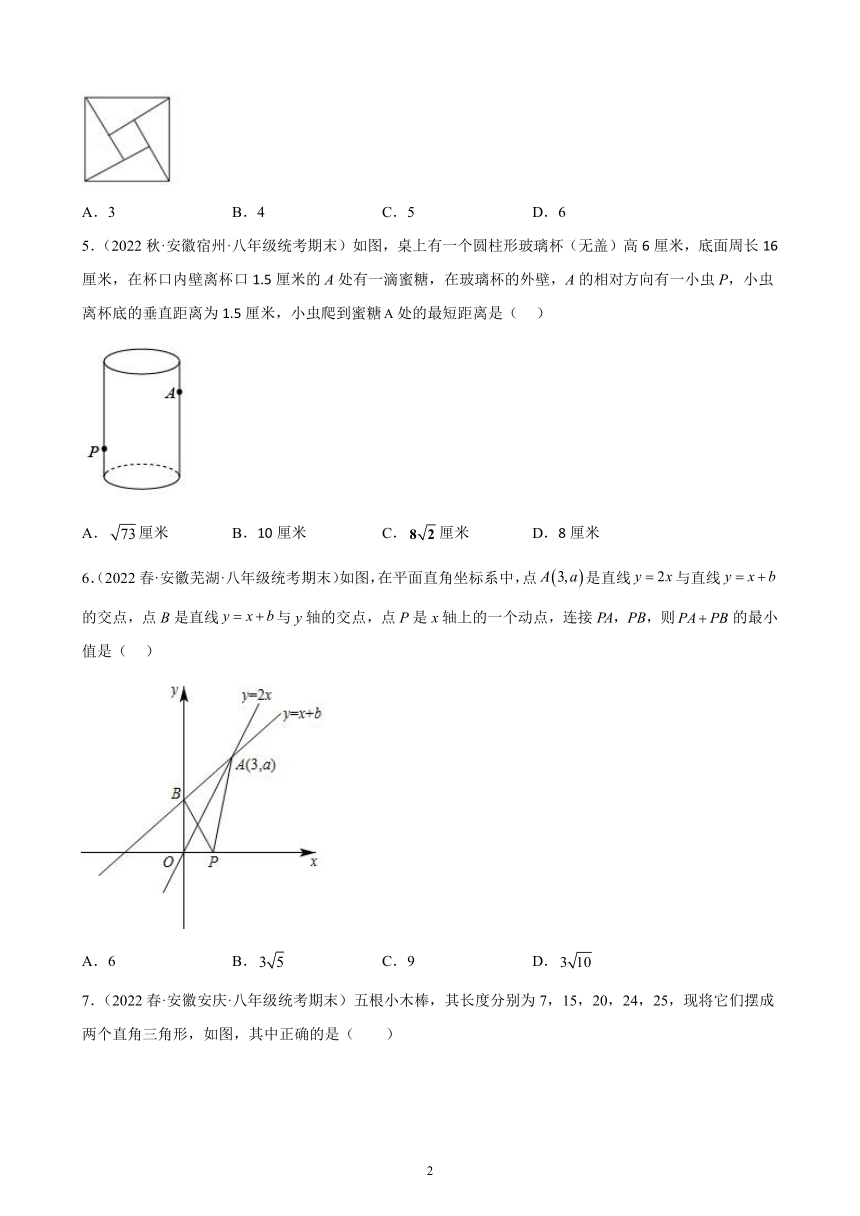
4.(2022春·安徽安庆·八年级统考期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
5.(2022秋·安徽宿州·八年级统考期末)如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
6.(2022春·安徽芜湖·八年级统考期末)如图,在平面直角坐标系中,点是直线与直线的交点,点B是直线与y轴的交点,点P是x轴上的一个动点,连接PA,PB,则的最小值是( )
A.6 B. C.9 D.
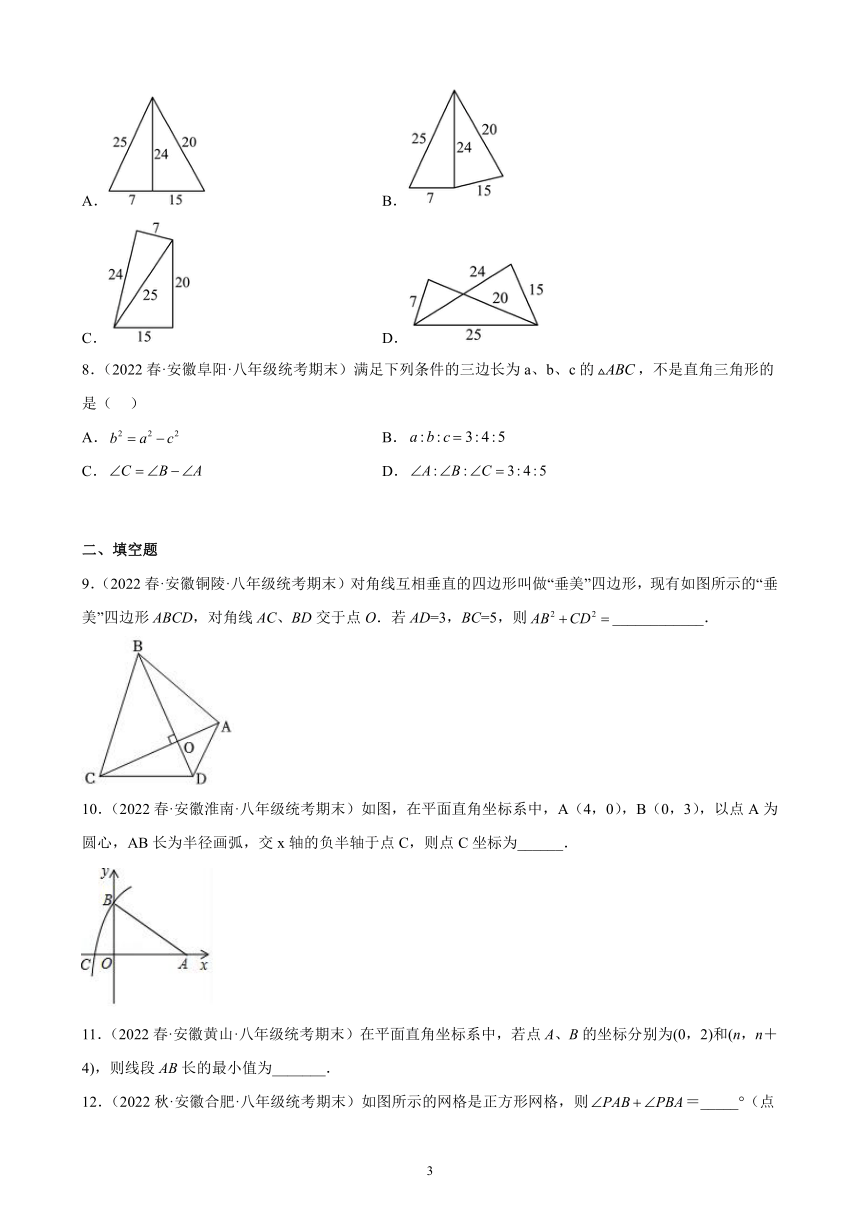
7.(2022春·安徽安庆·八年级统考期末)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
8.(2022春·安徽阜阳·八年级统考期末)满足下列条件的三边长为a、b、c的,不是直角三角形的是( )
A. B.
C. D.
二、填空题
9.(2022春·安徽铜陵·八年级统考期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=3,BC=5,则____________.
10.(2022春·安徽淮南·八年级统考期末)如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为______.
11.(2022春·安徽黄山·八年级统考期末)在平面直角坐标系中,若点A、B的坐标分别为(0,2)和(n,n+4),则线段AB长的最小值为_______.
12.(2022秋·安徽合肥·八年级统考期末)如图所示的网格是正方形网格,则=_____°(点A,B,P是网格线交点).
13.(2022春·安徽合肥·八年级统考期末)如图,在△ABC中,∠ACB=90°,以它的三边为边分别向外作正方形,面积分别为S1,S2,S3,已知S1=5,S2=12,则S3=_____.
14.(2022春·安徽宣城·八年级统考期末)如图,在校园内有两棵树相距12米,一棵树高14米,另一棵树高9米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞______米.
15.(2022春·安徽安庆·八年级统考期末)如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点A和点C嵌有一圈红丝线,则这圈红丝线的周长最小为___________.
16.(2022秋·安徽合肥·八年级统考期末)如图所示的网格是正方形网格,图形的各个顶点均为格点,则_____.
17.(2022春·安徽淮南·八年级统考期末)若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为___________. .
18.(2022春·安徽宣城·八年级统考期末)如图,在四边形ABCD中,,,,.则的度数为________.
三、解答题
19.(2022秋·安徽合肥·八年级统考期末)如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动.
(1)求线段DP的最小值;
(2)当DP最小时,求CDP的面积.
20.(2022春·安徽阜阳·八年级统考期末)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中夹,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其底面是边长是10尺的正方形,一根芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
21.(2022春·安徽合肥·八年级统考期末)某班将本校的办学理念“学会生活,学会学习,学会做人”做成宣传牌AB,放置在教室的黑板上方(如图所示),在一次活动中,小明搬来一架2.5米长的梯子AE,靠在宣传牌AB的顶部A处,底端落在地板E处,然后移动梯子使顶端落在宣传牌AB的底部B处,而底端E向外移了0.5米到C处(即CE=0.5米).已知黑板的上边距地板高度BM=2米.求宣传牌的顶部A距地板的高度AM为多少米(结果保留根号).
22.(2022春·安徽淮南·八年级统考期末)如图,小东将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约4米,请算出旗杆的高度.
23.(2022春·安徽合肥·八年级统考期末)如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB.
24.(2022春·安徽芜湖·八年级统考期末)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)试判断△ABC的形状,并说明理由;
(2)在格点上找一点D,使四边形ABCD是平行四边形,请画出这个四边形ABCD.
25.(2022春·安徽铜陵·八年级统考期末)如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
26.(2022秋·安徽宿州·八年级统考期末)如图,在四边形ABCD中,∠ABC=90°,AB=BC=2,CD=1,DA=3.求∠BCD的度数.
27.(2022春·安徽安庆·八年级统考期末)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A、B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得CA=750米,CD=600米,AD=450米.
(1)问CD是否为从村庄C到河边最近的路?请通过计算加以说明;
(2)求原来的路线BC的长.
28.(2022春·安徽宣城·八年级统考期末)在喜迎第七届军运会中,东西湖区加大绿化力度,在五环体育中心有一块空地,如图所示的四边形ABCD,现计划在空地上种植草皮,经测量AB=3m,BC=4m,CD=12m,DA=13m,,若每平方米草皮需要100元,求这块地种植草皮需要投入多少元?
参考答案:
1.C
【分析】首先过作,当与重合时,最短,首先利用等腰三角形的性质可得,进而可得的长,利用勾股定理计算出长,然后可得的取值范围,进而可得答案.
【详解】解:过作,
,
,
,
是线段上的动点(不含端点、.
,
或4,
线段长为正整数,
的可以有三条,长为4,3,4,
点的个数共有3个,
故选:C.
【点睛】本题主要考查了等腰三角形的性质和勾股定理,解题的关键是正确利用勾股定理计算出的最小值,然后求出的取值范围.
2.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
3.B
【分析】根据“在Rt△ABC中”和“沿BD进行翻折”可知,本题考查勾股定理和翻折问题,根据勾股定理和翻折的性质,运用方程的方法进行求解.
【详解】∵∠A=90°,AB=6,AC=8,
∴BC==10,
根据翻折的性质可得A′B=AB=6,A′D=AD,
∴A′C=10-6=4.
设CD=x,则A′D=8-x,
根据勾股定理可得x2-(8-x)2=42,
解得x=5,
故CD=5.
故答案为:B.
【点睛】本题考查勾股定理和翻折问题,根据勾股定理把求线段的长的问题转化为方程问题是解决本题的关键.
4.C
【详解】解:如图所示,∵(a+b)2=21
∴a2+2ab+b2=21,
∵大正方形的面积为13,即:a2+b2=13,
∴2ab=21﹣13=8,
∴小正方形的面积为13﹣8=5.
故选C.
5.B
【分析】把圆柱沿着点A所在母线展开,把圆柱上最短距离转化为将军饮马河型最短问题求解即可.
【详解】把圆柱沿着点A所在母线展开,如图所示,
作点A的对称点B,
连接PB,
则PB为所求,
根据题意,得PC=8,BC=6,
根据勾股定理,得PB=10,
故选B.
【点睛】本题考查了圆柱上的最短问题,利用圆柱展开,把问题转化为将军饮马河问题,灵活使用勾股定理是解题的关键.
6.D
【分析】作点A关于x轴的对称点A',连接A'B,则PA+PB的最小值即为A'B的长,先求出点A坐标,再待定系数法求出b的值,根据轴对称的性质可得点A'的坐标,进一步求出A'B的长,即可确定PA+PB的最小值.
【详解】解:作点A关于x轴的对称点,连接,如图所示:
则PA+PB的最小值即为的长,
将点A(3,a)代入y=2x,
得a=2×3=6,
∴点A坐标为(3,6),
将点A(3,6)代入y=x+b,
得3+b=6,
解得b=3,
∴点B坐标为(0,3),
根据轴对称的性质,可得点A'坐标为(3,-6)
∴,
∴PA+PB的最小值为.
故选:D.
【点睛】本题考查了一次函数的综合应用,涉及两直线的交点问题,一次函数的性质,利用轴对称解决最短路径问题,熟练掌握轴对称的性质以及一次函数的性质是解题的关键.
7.C
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、,,,故A不正确,不符合题意;
B、,,故B不正确,不符合题意;
C、,,故C正确,符合题意;
D、,,故D不正确,不符合题意.
故选:C.
【点睛】本题考查了勾股定理逆定理,熟练掌握勾股定理是解本题的关键.
8.D
【分析】根据勾股定理的逆定理及三角形内角和定理逐项判断即可.
【详解】解:A.∵ ,∴,是直角三角形,故A选项不符合题意;
B. ∵,,∴,是直角三角形,故B选项不符合题意;
C. ∵,∴,是直角三角形,故C选项不符合题意;
D. ∵,∴,不是直角三角形,故D符合题意.
故选:D.
【点睛】本题考查勾股定理的逆定理及三角形内角和定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
9.34
【分析】在Rt△COB和Rt△AOB中,根据勾股定理得BO2+CO2=CB2,OD2+OA2=AD2,进一步得BO2+CO2+OD2+OA2=9+25,再根据AB2=BO2+AO2,CD2=OC2+OD2,最后求得AB2+CD2=34.
【详解】解:∵BD⊥AC,
∴∠COB=∠AOB=∠AOD=∠COD=90°,
在Rt△COB和Rt△AOB中,根据勾股定理得,
BO2+CO2=CB2,OD2+OA2=AD2,
∴BO2+CO2+OD2+OA2=9+25,
∵AB2=BO2+AO2,CD2=OC2+OD2,
∴AB2+CD2=34;
故答案为:34.
【点睛】本题考查勾股定理的应用,熟练掌握勾股定理在实际问题中的应用,从题中抽象出勾股定理这一数学模型是解题关键.
10.(﹣1,0)
【分析】根据勾股定理求出AB的长,由AB=AC即可求出C点坐标.
【详解】解:∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB==5
∴AC=5,
∴点C的横坐标为:4-5=-1,纵坐标为:0,
∴点C的坐标为(-1,0).
故答案为(-1,0).
【点睛】本题考查了勾股定理和坐标与图形性质的应用, 解此题的关键是求出的长, 注意: 在直角三角形中, 两直角边的平方和等于斜边的平方 .
11.
【分析】根据点A、B的坐标分别为(0,2)和(n,n+4),利用勾股定理可以表示出AB的长,然后化简,即可得到AB的最小值.
【详解】解:∵点A、B的坐标分别为(0,2)和(n,n+4),
∴AB=
,
∵≥0,
∴当n=-1时,AB的最小值为,
故答案为:.
【点睛】本题考查了勾股定理的应用,完全平方公式的应用,掌握勾股定理,两点的距离公式是解题的关键.
12.45
【分析】延长AP交格点于D,连接BD,根据勾股定理得到PD2=BD2=1+22=5,PB2=12+32=10,求得PD2+DB2=PB2,于是得到∠PDB=90°,根据三角形外角的性质即可得到结论.
【详解】解:延长AP交格点于D,连接BD,
则PD2=BD2=1+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
即△PBD为等腰直角三角形,
∴∠DPB=∠PAB+∠PBA=45°,
故答案为:45.
【点睛】本题考查了勾股定理的逆定理,勾股定理,三角形的外角的性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.
13.17
【分析】根据勾股定理即可得到结论.
【详解】解:∵∠ACB=90°,S1=5,S2=12,
∴AC2=5,BC2=12,
∴AB2=AC2+BC2=5+12=17,
∴S3=17,
故答案为:17.
【点睛】本题考查了勾股定理,正方形的面积,正确的识别图形是解题的关键.
14.13
【分析】根据“两点之间线段最短”可知:小鸟沿着两棵树的顶端进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
【详解】如图所示,
AB,CD为树,且AB=14米,CD=9米,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=12,AE=AB CD=5,
在直角三角形AEC中,
AC===13.
答:小鸟至少要飞13米.
故答案为:13.
【点睛】本题考查了勾股定理的应用,关键是从实际问题中构建出数学模型,转化为数学知识,然后利用直角三角形的性质解题.
15.26
【分析】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
【详解】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为24dm,圆柱高为5dm,
∴AB=5dm,BC=BC′=12dm,
∴AC2=52+122=132,
∴AC=5.
∴这圈金属丝的周长最小为2AC=26(dm).
故答案为:26.
【点睛】本题考查了勾股定理求最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题把圆柱的侧面展开成矩形,“化曲面为平面”是解题的关键.
16.##度
【分析】利用勾股定理的逆定理先证明 再证明,进而得出答案.
【详解】解:如图所示: 连接
由勾股定理可得:
∴
∴
∴ 而
∴
∴
故答案为:.
【点睛】本题考查的是勾股定理的应用,勾股定理的逆定理的应用,等腰直角三角形的性质,三角形的内角和定理的应用,证明是解本题的关键.
17.120 cm
【分析】设三边的长是,,,根据周长即可求得x的值,则三角形的三边的长即可求得,然后利用勾股定理的逆定理判断三角形是直角三角形,然后利用面积公式求解.
【详解】设三边的长是,,,
则,
解得:,
则三边长是10 cm,24 cm,26 cm.
∵
∴三角形是直角三角形,
∴三角形的面积是(cm)
故答案为:120 cm
【点睛】考查勾股定理逆定理的理解与运用,熟练掌握勾股定理的逆定理是解题的关键.
18.135°##135度
【分析】如图连接BD,∠ABD=∠ADB=45°,勾股定理知BD的长,BC、BD、CD三边满足勾股定理,知∠DBC=90°,进而求出∠ABC的值即可.
【详解】解:如图连接BD,
∵∠A=90°,AD=AB=2
∴∠ABD=∠ADB=45°,BD2
∵BC,CD
∴BC2+BD2=()2+(2)2=()2=CD2
∴△DBC是直角三角形
∴∠DBC=90°
∴∠ABC=∠ABD+∠DBC=45°+90°=135°
∴∠ABC的度数是135°.
故答案为:135°
【点睛】本题考查了等腰三角形的性质,勾股定理以及勾股定理的逆定理;解题的关键在于用勾股定理的逆定理说明三角形为直角三角形.
19.(1)DP的最小值是3;
(2)当DP最小时,△CDP的面积为12.
【分析】(1)由垂线段最短可知当DP⊥BC时,DP最短,根据角平分线的性质即可得出结论;
(2)由勾股定理得BD=5,当DP最小时,DP⊥BC,再由勾股定理得PB=4,则CP=BC-PB=8,然后由三角形面积公式即可求解.
【详解】(1)解:当DP⊥BC时,线段DP的值最小,
∵BD平分∠ABC,∠A=90°,
当DP⊥BC时,DP=AD,
∵AD=3,
∴DP的最小值是3;
(2)解:∵∠A=90°,
∴BD==5,
当DP最小时,DP=3,DP⊥BC,
则∠DPB=∠DPC=90°,
∴PB==4,
∴CP=BC-PB=12-4=8,
∴△CDP的面积=CP×DP=×8×3=12,
即当DP最小时,△CDP的面积为12.
【点睛】本题考查了勾股定理、角平分线的性质、垂线段最短以及三角形面积等知识,熟练掌握勾股定理和角平分线的在是解题的关键.
20.水深12尺,芦苇长13尺
【分析】依题意画出图形,设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,因为B'E=10尺,所以B'C=5尺,利用勾股定理求出x的值即可得到答案.
【详解】解:依题意画出图形,如下图,
设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,
因为B'E=10尺,所以B'C=5尺,
在Rt△ACB'中,52+(x-1)2=x2,
解得:x=13,
即水深12尺,芦苇长13尺.
【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键.
21.米
【分析】在Rt△MBC中,利用勾股定理得出CM,再在Rt△AEM中,利用勾股定理可求解AM的长.
【详解】解:由题意可得:AE=BC=2.5米,BM=2米,EC=0.5米,
在Rt△MBC中,MC=(米),
则EM=1.5-0.5=1(米),
在Rt△AEM中,AM=(米),
答:宣传牌的顶部A距地板的高度AM为米
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
22.旗杆的高度为16米
【分析】设旗杆的高度为x米,根据勾股定理列出方程,然后解方程即可求解.
【详解】解:设旗杆的高度为x米,则绳长为(x+4)米,
由勾股定理得:x2+122=(x+4)2,
解得:x=16,
答:旗杆的高度为16米.
【点睛】本题考查勾股定理的应用、解一元一次方程,读懂题意,利用勾股定理列出方程是解答的关键.
23.风筝距离地面的高度AB为12米
【分析】设AB=x米,则AC=(x+1)米,依据勾股定理即可得到方程,进而得出风筝距离地面的高度AB.
【详解】解:设AB=x米,则AC=(x+1)米,
由图可得,∠ABC=90°,BC=5米,
在Rt△ABC中,,
即,
解得x=12,
答:风筝距离地面的高度AB为12米.
【点睛】本题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
24.(1)△ABC是直角三角形,理由见解析
(2)见解析
【分析】(1)由勾股定理的逆定理进行证明;
(2)根据由平行四边形的判定画图即可
(1)
由图形知:,,,
∴,
∴,
∴△ABC是直角三角形,
∴;
(2)
如图所示,四边形ABCD就是所求作的平行四边形.
【点睛】此题考查直角三角形的判定和性质、特殊四边形的判定及作图能力,综合性较强.
25.
【分析】连接,根据勾股定理求得的长,根据勾股定理的逆定理可得,根据,即可求解.
【详解】解:连接,
∵
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴.
【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键.
26.∠BCD=135°.
【分析】连接AC,∠ABC=90°和AB=BC求出∠ACB=45°,根据勾股定理的逆定理证明△ACD为直角三角形,求出∠ACD=90°,即可解决.
【详解】连接AC,
∵∠ABC=90°,AB=BC=2,
∴∠ACB=45°,AC2=AB 2+BC2=8,
在△ABC中,
∵AC2+CD2=8+1=9=DA2,
∴△ACD为直角三角形,∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=135°.
【点睛】该题主要考查了勾股定理的逆定理、等腰直角三角形的性质.能作辅助线AC并根据勾股定理逆定理证明△ACD为直角三角形是解决此题的关键.
27.(1)是从村庄到河边最近的路,理由见解析
(2)米
【分析】(1)结合已知条件根据勾股定理的逆定理、垂直的定义、垂线段最短即可得解;
(2)设米,则米、米,根据勾股定理列出关于的方程求解即可.
(1)
解:结论:是从村庄到河边最近的路.
理由: ∵在中,米,米,米,
∴,即,
∴是直角三角形,
∴.
∴.
∴是从村庄到河边最近的路.
(2)
设米,则米,米,
∵在中,由勾股定理得:.
∴.
∴.
答:原来的路线的长为米.
【点睛】本题考查了勾股定理以及其逆定理、垂直的定义、垂线段最短、利用方程求线段长等知识点,熟练掌握相关知识点是解决问题的关键.
28.3600元
【分析】先利用勾股定理得出AC,再利用勾股定理的逆定理得出∠ACD=90°,根据四边形面积等于两直角三角形面积和即可求出面积,由面积可计算投入.
【详解】解:连接AC,
∵,,,
∴,
∵,
∴是直角三角形,,
∴四边形的面积为,
∴学校要投入的资金为(元).
【点睛】本题考查勾股定理及勾股定理的逆定理,正确得出△ACD是直角三角形是解题的关键.
一、单选题
1.(2022春·安徽蚌埠·八年级统考期末)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
2.(2022春·安徽滁州·八年级统考期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
3.(2022春·安徽铜陵·八年级统考期末)如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,现将Rt△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( )
A.10 B.5 C.4 D.3
4.(2022春·安徽安庆·八年级统考期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A.3 B.4 C.5 D.6
5.(2022秋·安徽宿州·八年级统考期末)如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
6.(2022春·安徽芜湖·八年级统考期末)如图,在平面直角坐标系中,点是直线与直线的交点,点B是直线与y轴的交点,点P是x轴上的一个动点,连接PA,PB,则的最小值是( )
A.6 B. C.9 D.
7.(2022春·安徽安庆·八年级统考期末)五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
8.(2022春·安徽阜阳·八年级统考期末)满足下列条件的三边长为a、b、c的,不是直角三角形的是( )
A. B.
C. D.
二、填空题
9.(2022春·安徽铜陵·八年级统考期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=3,BC=5,则____________.
10.(2022春·安徽淮南·八年级统考期末)如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为______.
11.(2022春·安徽黄山·八年级统考期末)在平面直角坐标系中,若点A、B的坐标分别为(0,2)和(n,n+4),则线段AB长的最小值为_______.
12.(2022秋·安徽合肥·八年级统考期末)如图所示的网格是正方形网格,则=_____°(点A,B,P是网格线交点).
13.(2022春·安徽合肥·八年级统考期末)如图,在△ABC中,∠ACB=90°,以它的三边为边分别向外作正方形,面积分别为S1,S2,S3,已知S1=5,S2=12,则S3=_____.
14.(2022春·安徽宣城·八年级统考期末)如图,在校园内有两棵树相距12米,一棵树高14米,另一棵树高9米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞______米.
15.(2022春·安徽安庆·八年级统考期末)如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点A和点C嵌有一圈红丝线,则这圈红丝线的周长最小为___________.
16.(2022秋·安徽合肥·八年级统考期末)如图所示的网格是正方形网格,图形的各个顶点均为格点,则_____.
17.(2022春·安徽淮南·八年级统考期末)若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为___________. .
18.(2022春·安徽宣城·八年级统考期末)如图,在四边形ABCD中,,,,.则的度数为________.
三、解答题
19.(2022秋·安徽合肥·八年级统考期末)如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动.
(1)求线段DP的最小值;
(2)当DP最小时,求CDP的面积.
20.(2022春·安徽阜阳·八年级统考期末)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中夹,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其底面是边长是10尺的正方形,一根芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
21.(2022春·安徽合肥·八年级统考期末)某班将本校的办学理念“学会生活,学会学习,学会做人”做成宣传牌AB,放置在教室的黑板上方(如图所示),在一次活动中,小明搬来一架2.5米长的梯子AE,靠在宣传牌AB的顶部A处,底端落在地板E处,然后移动梯子使顶端落在宣传牌AB的底部B处,而底端E向外移了0.5米到C处(即CE=0.5米).已知黑板的上边距地板高度BM=2米.求宣传牌的顶部A距地板的高度AM为多少米(结果保留根号).
22.(2022春·安徽淮南·八年级统考期末)如图,小东将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约4米,请算出旗杆的高度.
23.(2022春·安徽合肥·八年级统考期末)如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB.
24.(2022春·安徽芜湖·八年级统考期末)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)试判断△ABC的形状,并说明理由;
(2)在格点上找一点D,使四边形ABCD是平行四边形,请画出这个四边形ABCD.
25.(2022春·安徽铜陵·八年级统考期末)如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
26.(2022秋·安徽宿州·八年级统考期末)如图,在四边形ABCD中,∠ABC=90°,AB=BC=2,CD=1,DA=3.求∠BCD的度数.
27.(2022春·安徽安庆·八年级统考期末)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A、B,其中AB=BC,由于某种原因,由C到B的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得CA=750米,CD=600米,AD=450米.
(1)问CD是否为从村庄C到河边最近的路?请通过计算加以说明;
(2)求原来的路线BC的长.
28.(2022春·安徽宣城·八年级统考期末)在喜迎第七届军运会中,东西湖区加大绿化力度,在五环体育中心有一块空地,如图所示的四边形ABCD,现计划在空地上种植草皮,经测量AB=3m,BC=4m,CD=12m,DA=13m,,若每平方米草皮需要100元,求这块地种植草皮需要投入多少元?
参考答案:
1.C
【分析】首先过作,当与重合时,最短,首先利用等腰三角形的性质可得,进而可得的长,利用勾股定理计算出长,然后可得的取值范围,进而可得答案.
【详解】解:过作,
,
,
,
是线段上的动点(不含端点、.
,
或4,
线段长为正整数,
的可以有三条,长为4,3,4,
点的个数共有3个,
故选:C.
【点睛】本题主要考查了等腰三角形的性质和勾股定理,解题的关键是正确利用勾股定理计算出的最小值,然后求出的取值范围.
2.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
3.B
【分析】根据“在Rt△ABC中”和“沿BD进行翻折”可知,本题考查勾股定理和翻折问题,根据勾股定理和翻折的性质,运用方程的方法进行求解.
【详解】∵∠A=90°,AB=6,AC=8,
∴BC==10,
根据翻折的性质可得A′B=AB=6,A′D=AD,
∴A′C=10-6=4.
设CD=x,则A′D=8-x,
根据勾股定理可得x2-(8-x)2=42,
解得x=5,
故CD=5.
故答案为:B.
【点睛】本题考查勾股定理和翻折问题,根据勾股定理把求线段的长的问题转化为方程问题是解决本题的关键.
4.C
【详解】解:如图所示,∵(a+b)2=21
∴a2+2ab+b2=21,
∵大正方形的面积为13,即:a2+b2=13,
∴2ab=21﹣13=8,
∴小正方形的面积为13﹣8=5.
故选C.
5.B
【分析】把圆柱沿着点A所在母线展开,把圆柱上最短距离转化为将军饮马河型最短问题求解即可.
【详解】把圆柱沿着点A所在母线展开,如图所示,
作点A的对称点B,
连接PB,
则PB为所求,
根据题意,得PC=8,BC=6,
根据勾股定理,得PB=10,
故选B.
【点睛】本题考查了圆柱上的最短问题,利用圆柱展开,把问题转化为将军饮马河问题,灵活使用勾股定理是解题的关键.
6.D
【分析】作点A关于x轴的对称点A',连接A'B,则PA+PB的最小值即为A'B的长,先求出点A坐标,再待定系数法求出b的值,根据轴对称的性质可得点A'的坐标,进一步求出A'B的长,即可确定PA+PB的最小值.
【详解】解:作点A关于x轴的对称点,连接,如图所示:
则PA+PB的最小值即为的长,
将点A(3,a)代入y=2x,
得a=2×3=6,
∴点A坐标为(3,6),
将点A(3,6)代入y=x+b,
得3+b=6,
解得b=3,
∴点B坐标为(0,3),
根据轴对称的性质,可得点A'坐标为(3,-6)
∴,
∴PA+PB的最小值为.
故选:D.
【点睛】本题考查了一次函数的综合应用,涉及两直线的交点问题,一次函数的性质,利用轴对称解决最短路径问题,熟练掌握轴对称的性质以及一次函数的性质是解题的关键.
7.C
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、,,,故A不正确,不符合题意;
B、,,故B不正确,不符合题意;
C、,,故C正确,符合题意;
D、,,故D不正确,不符合题意.
故选:C.
【点睛】本题考查了勾股定理逆定理,熟练掌握勾股定理是解本题的关键.
8.D
【分析】根据勾股定理的逆定理及三角形内角和定理逐项判断即可.
【详解】解:A.∵ ,∴,是直角三角形,故A选项不符合题意;
B. ∵,,∴,是直角三角形,故B选项不符合题意;
C. ∵,∴,是直角三角形,故C选项不符合题意;
D. ∵,∴,不是直角三角形,故D符合题意.
故选:D.
【点睛】本题考查勾股定理的逆定理及三角形内角和定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
9.34
【分析】在Rt△COB和Rt△AOB中,根据勾股定理得BO2+CO2=CB2,OD2+OA2=AD2,进一步得BO2+CO2+OD2+OA2=9+25,再根据AB2=BO2+AO2,CD2=OC2+OD2,最后求得AB2+CD2=34.
【详解】解:∵BD⊥AC,
∴∠COB=∠AOB=∠AOD=∠COD=90°,
在Rt△COB和Rt△AOB中,根据勾股定理得,
BO2+CO2=CB2,OD2+OA2=AD2,
∴BO2+CO2+OD2+OA2=9+25,
∵AB2=BO2+AO2,CD2=OC2+OD2,
∴AB2+CD2=34;
故答案为:34.
【点睛】本题考查勾股定理的应用,熟练掌握勾股定理在实际问题中的应用,从题中抽象出勾股定理这一数学模型是解题关键.
10.(﹣1,0)
【分析】根据勾股定理求出AB的长,由AB=AC即可求出C点坐标.
【详解】解:∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB==5
∴AC=5,
∴点C的横坐标为:4-5=-1,纵坐标为:0,
∴点C的坐标为(-1,0).
故答案为(-1,0).
【点睛】本题考查了勾股定理和坐标与图形性质的应用, 解此题的关键是求出的长, 注意: 在直角三角形中, 两直角边的平方和等于斜边的平方 .
11.
【分析】根据点A、B的坐标分别为(0,2)和(n,n+4),利用勾股定理可以表示出AB的长,然后化简,即可得到AB的最小值.
【详解】解:∵点A、B的坐标分别为(0,2)和(n,n+4),
∴AB=
,
∵≥0,
∴当n=-1时,AB的最小值为,
故答案为:.
【点睛】本题考查了勾股定理的应用,完全平方公式的应用,掌握勾股定理,两点的距离公式是解题的关键.
12.45
【分析】延长AP交格点于D,连接BD,根据勾股定理得到PD2=BD2=1+22=5,PB2=12+32=10,求得PD2+DB2=PB2,于是得到∠PDB=90°,根据三角形外角的性质即可得到结论.
【详解】解:延长AP交格点于D,连接BD,
则PD2=BD2=1+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
即△PBD为等腰直角三角形,
∴∠DPB=∠PAB+∠PBA=45°,
故答案为:45.
【点睛】本题考查了勾股定理的逆定理,勾股定理,三角形的外角的性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.
13.17
【分析】根据勾股定理即可得到结论.
【详解】解:∵∠ACB=90°,S1=5,S2=12,
∴AC2=5,BC2=12,
∴AB2=AC2+BC2=5+12=17,
∴S3=17,
故答案为:17.
【点睛】本题考查了勾股定理,正方形的面积,正确的识别图形是解题的关键.
14.13
【分析】根据“两点之间线段最短”可知:小鸟沿着两棵树的顶端进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
【详解】如图所示,
AB,CD为树,且AB=14米,CD=9米,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=12,AE=AB CD=5,
在直角三角形AEC中,
AC===13.
答:小鸟至少要飞13米.
故答案为:13.
【点睛】本题考查了勾股定理的应用,关键是从实际问题中构建出数学模型,转化为数学知识,然后利用直角三角形的性质解题.
15.26
【分析】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
【详解】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为24dm,圆柱高为5dm,
∴AB=5dm,BC=BC′=12dm,
∴AC2=52+122=132,
∴AC=5.
∴这圈金属丝的周长最小为2AC=26(dm).
故答案为:26.
【点睛】本题考查了勾股定理求最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题把圆柱的侧面展开成矩形,“化曲面为平面”是解题的关键.
16.##度
【分析】利用勾股定理的逆定理先证明 再证明,进而得出答案.
【详解】解:如图所示: 连接
由勾股定理可得:
∴
∴
∴ 而
∴
∴
故答案为:.
【点睛】本题考查的是勾股定理的应用,勾股定理的逆定理的应用,等腰直角三角形的性质,三角形的内角和定理的应用,证明是解本题的关键.
17.120 cm
【分析】设三边的长是,,,根据周长即可求得x的值,则三角形的三边的长即可求得,然后利用勾股定理的逆定理判断三角形是直角三角形,然后利用面积公式求解.
【详解】设三边的长是,,,
则,
解得:,
则三边长是10 cm,24 cm,26 cm.
∵
∴三角形是直角三角形,
∴三角形的面积是(cm)
故答案为:120 cm
【点睛】考查勾股定理逆定理的理解与运用,熟练掌握勾股定理的逆定理是解题的关键.
18.135°##135度
【分析】如图连接BD,∠ABD=∠ADB=45°,勾股定理知BD的长,BC、BD、CD三边满足勾股定理,知∠DBC=90°,进而求出∠ABC的值即可.
【详解】解:如图连接BD,
∵∠A=90°,AD=AB=2
∴∠ABD=∠ADB=45°,BD2
∵BC,CD
∴BC2+BD2=()2+(2)2=()2=CD2
∴△DBC是直角三角形
∴∠DBC=90°
∴∠ABC=∠ABD+∠DBC=45°+90°=135°
∴∠ABC的度数是135°.
故答案为:135°
【点睛】本题考查了等腰三角形的性质,勾股定理以及勾股定理的逆定理;解题的关键在于用勾股定理的逆定理说明三角形为直角三角形.
19.(1)DP的最小值是3;
(2)当DP最小时,△CDP的面积为12.
【分析】(1)由垂线段最短可知当DP⊥BC时,DP最短,根据角平分线的性质即可得出结论;
(2)由勾股定理得BD=5,当DP最小时,DP⊥BC,再由勾股定理得PB=4,则CP=BC-PB=8,然后由三角形面积公式即可求解.
【详解】(1)解:当DP⊥BC时,线段DP的值最小,
∵BD平分∠ABC,∠A=90°,
当DP⊥BC时,DP=AD,
∵AD=3,
∴DP的最小值是3;
(2)解:∵∠A=90°,
∴BD==5,
当DP最小时,DP=3,DP⊥BC,
则∠DPB=∠DPC=90°,
∴PB==4,
∴CP=BC-PB=12-4=8,
∴△CDP的面积=CP×DP=×8×3=12,
即当DP最小时,△CDP的面积为12.
【点睛】本题考查了勾股定理、角平分线的性质、垂线段最短以及三角形面积等知识,熟练掌握勾股定理和角平分线的在是解题的关键.
20.水深12尺,芦苇长13尺
【分析】依题意画出图形,设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,因为B'E=10尺,所以B'C=5尺,利用勾股定理求出x的值即可得到答案.
【详解】解:依题意画出图形,如下图,
设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,
因为B'E=10尺,所以B'C=5尺,
在Rt△ACB'中,52+(x-1)2=x2,
解得:x=13,
即水深12尺,芦苇长13尺.
【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键.
21.米
【分析】在Rt△MBC中,利用勾股定理得出CM,再在Rt△AEM中,利用勾股定理可求解AM的长.
【详解】解:由题意可得:AE=BC=2.5米,BM=2米,EC=0.5米,
在Rt△MBC中,MC=(米),
则EM=1.5-0.5=1(米),
在Rt△AEM中,AM=(米),
答:宣传牌的顶部A距地板的高度AM为米
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
22.旗杆的高度为16米
【分析】设旗杆的高度为x米,根据勾股定理列出方程,然后解方程即可求解.
【详解】解:设旗杆的高度为x米,则绳长为(x+4)米,
由勾股定理得:x2+122=(x+4)2,
解得:x=16,
答:旗杆的高度为16米.
【点睛】本题考查勾股定理的应用、解一元一次方程,读懂题意,利用勾股定理列出方程是解答的关键.
23.风筝距离地面的高度AB为12米
【分析】设AB=x米,则AC=(x+1)米,依据勾股定理即可得到方程,进而得出风筝距离地面的高度AB.
【详解】解:设AB=x米,则AC=(x+1)米,
由图可得,∠ABC=90°,BC=5米,
在Rt△ABC中,,
即,
解得x=12,
答:风筝距离地面的高度AB为12米.
【点睛】本题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
24.(1)△ABC是直角三角形,理由见解析
(2)见解析
【分析】(1)由勾股定理的逆定理进行证明;
(2)根据由平行四边形的判定画图即可
(1)
由图形知:,,,
∴,
∴,
∴△ABC是直角三角形,
∴;
(2)
如图所示,四边形ABCD就是所求作的平行四边形.
【点睛】此题考查直角三角形的判定和性质、特殊四边形的判定及作图能力,综合性较强.
25.
【分析】连接,根据勾股定理求得的长,根据勾股定理的逆定理可得,根据,即可求解.
【详解】解:连接,
∵
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴.
【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键.
26.∠BCD=135°.
【分析】连接AC,∠ABC=90°和AB=BC求出∠ACB=45°,根据勾股定理的逆定理证明△ACD为直角三角形,求出∠ACD=90°,即可解决.
【详解】连接AC,
∵∠ABC=90°,AB=BC=2,
∴∠ACB=45°,AC2=AB 2+BC2=8,
在△ABC中,
∵AC2+CD2=8+1=9=DA2,
∴△ACD为直角三角形,∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=135°.
【点睛】该题主要考查了勾股定理的逆定理、等腰直角三角形的性质.能作辅助线AC并根据勾股定理逆定理证明△ACD为直角三角形是解决此题的关键.
27.(1)是从村庄到河边最近的路,理由见解析
(2)米
【分析】(1)结合已知条件根据勾股定理的逆定理、垂直的定义、垂线段最短即可得解;
(2)设米,则米、米,根据勾股定理列出关于的方程求解即可.
(1)
解:结论:是从村庄到河边最近的路.
理由: ∵在中,米,米,米,
∴,即,
∴是直角三角形,
∴.
∴.
∴是从村庄到河边最近的路.
(2)
设米,则米,米,
∵在中,由勾股定理得:.
∴.
∴.
答:原来的路线的长为米.
【点睛】本题考查了勾股定理以及其逆定理、垂直的定义、垂线段最短、利用方程求线段长等知识点,熟练掌握相关知识点是解决问题的关键.
28.3600元
【分析】先利用勾股定理得出AC,再利用勾股定理的逆定理得出∠ACD=90°,根据四边形面积等于两直角三角形面积和即可求出面积,由面积可计算投入.
【详解】解:连接AC,
∵,,,
∴,
∵,
∴是直角三角形,,
∴四边形的面积为,
∴学校要投入的资金为(元).
【点睛】本题考查勾股定理及勾股定理的逆定理,正确得出△ACD是直角三角形是解题的关键.
