全等三角形的判定(2)[上学期]
文档属性
| 名称 | 全等三角形的判定(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 177.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-21 00:00:00 | ||
图片预览





文档简介
课件18张PPT。13.2 三角形全等的条件⑵
芜湖县埭南中学数学组制作2006.10.19知识回顾 上一节我们探究了两个
三角形满足三条边对应相等
时,这两个三角形全等,你
认为还有其他情况吗? 先任意画出一个△ABC,
再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A,A/C/ =AC。把画好
的△A/B/C/剪下,放到△ABC上,
它们全等吗?探究1已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC.画法:1、画∠DA/ E=∠A ;2、在射线A/ D上截取A/B/=AB,在射线
A/ E上截取A/C/=AC;3、连结B/C/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实? 探究反映的规律是:
两边和它们的夹角对应相等的
两个三角形全等
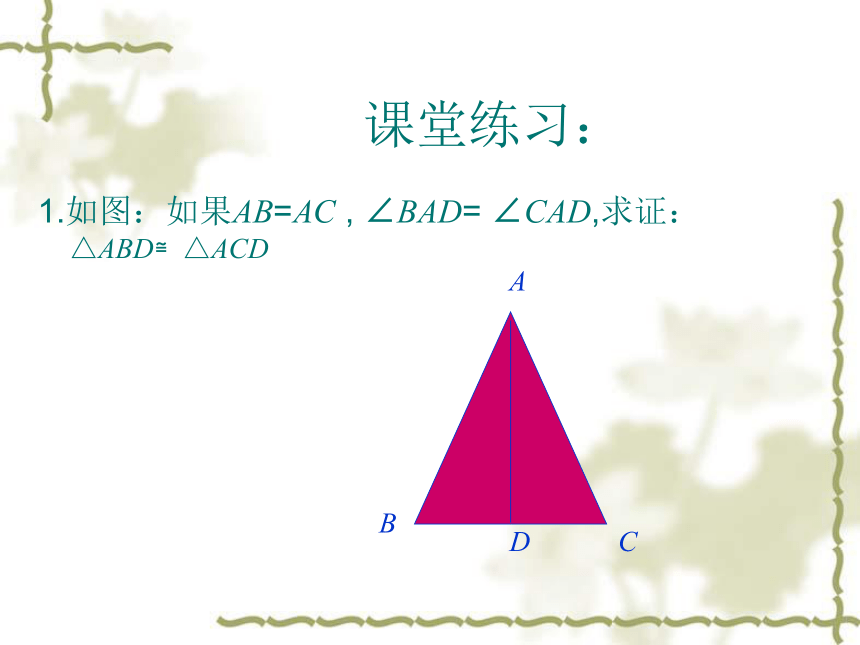
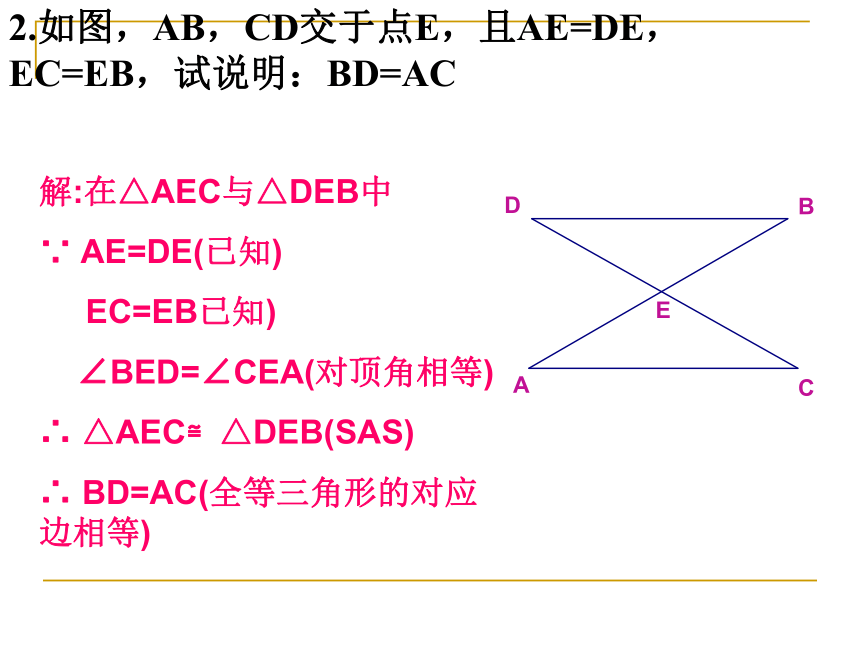
(简写成“边角边”或“SAS”)课堂练习:1.如图:如果AB=AC , ∠BAD= ∠CAD,求证: △ABD≌△ACDABCD2.如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)3.已知: 如图直线AC和直线BD相交于点O,OA=OC,OB=OD,求证:AB=CD OACBD知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?二、例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)ABD CE求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
∟ ADBCE变式1:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE. 求证: ⑴ △DAC≌△EABBE=DC
∠B= ∠ C
∠ D= ∠ E
BE⊥CD FMABCED变式2:已知,如图等边△AEB与等 边△BDC在线段AC的同侧 求证: △ABD≌△EBC变式3:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
证明:∵△ABD和△ACE是等边三角形
∴ AD=AB AC=AE
∠BAD=∠CAE=60°
∴∠BAD+∠BAC= ∠CAE+∠BAC
即∠BAC=∠DAE
在△ABE和△ADC
AD=AB
∠BAC=∠DAE
AC=AE
∴ △ABE≌△ADC (SAS)
∴DC=BE (全等三角形对应边相等)
﹛3.如图,AD⊥AB,AE⊥AC,且AD=AB,
AE=AC.试说明BE与CD的关系. 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究2ABCD要点复习与回顾:㈠1、边角边的内容是什么?
2、边角边的作用:
(证明两个三角形全等,也可间接证明线段,角相等)
3、怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角、平角等)]
总结:已知中找。图形中看 归纳小结:
l.利用全等三角形证明线段或角相等, 是证明 线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.
2.利用全等三角形解决实际问题的步骤:
⑴先确定实际问题应用哪些几何知识解决.
⑵根据实际抽象出几何图形.
⑶结合图形和题意写出已知,求证.
⑷经过分析,找出证明途径.
⑸写出证明过程.
作业:104页3、4、10
三角形满足三条边对应相等
时,这两个三角形全等,你
认为还有其他情况吗? 先任意画出一个△ABC,
再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A,A/C/ =AC。把画好
的△A/B/C/剪下,放到△ABC上,
它们全等吗?探究1已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC.画法:1、画∠DA/ E=∠A ;2、在射线A/ D上截取A/B/=AB,在射线
A/ E上截取A/C/=AC;3、连结B/C/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实? 探究反映的规律是:
两边和它们的夹角对应相等的
两个三角形全等
(简写成“边角边”或“SAS”)课堂练习:1.如图:如果AB=AC , ∠BAD= ∠CAD,求证: △ABD≌△ACDABCD2.如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)3.已知: 如图直线AC和直线BD相交于点O,OA=OC,OB=OD,求证:AB=CD OACBD知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?二、例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)ABD CE求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
∟ ADBCE变式1:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE. 求证: ⑴ △DAC≌△EABBE=DC
∠B= ∠ C
∠ D= ∠ E
BE⊥CD FMABCED变式2:已知,如图等边△AEB与等 边△BDC在线段AC的同侧 求证: △ABD≌△EBC变式3:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
证明:∵△ABD和△ACE是等边三角形
∴ AD=AB AC=AE
∠BAD=∠CAE=60°
∴∠BAD+∠BAC= ∠CAE+∠BAC
即∠BAC=∠DAE
在△ABE和△ADC
AD=AB
∠BAC=∠DAE
AC=AE
∴ △ABE≌△ADC (SAS)
∴DC=BE (全等三角形对应边相等)
﹛3.如图,AD⊥AB,AE⊥AC,且AD=AB,
AE=AC.试说明BE与CD的关系. 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究2ABCD要点复习与回顾:㈠1、边角边的内容是什么?
2、边角边的作用:
(证明两个三角形全等,也可间接证明线段,角相等)
3、怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角、平角等)]
总结:已知中找。图形中看 归纳小结:
l.利用全等三角形证明线段或角相等, 是证明 线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.
2.利用全等三角形解决实际问题的步骤:
⑴先确定实际问题应用哪些几何知识解决.
⑵根据实际抽象出几何图形.
⑶结合图形和题意写出已知,求证.
⑷经过分析,找出证明途径.
⑸写出证明过程.
作业:104页3、4、10
