8.1一元一次不等式的性质

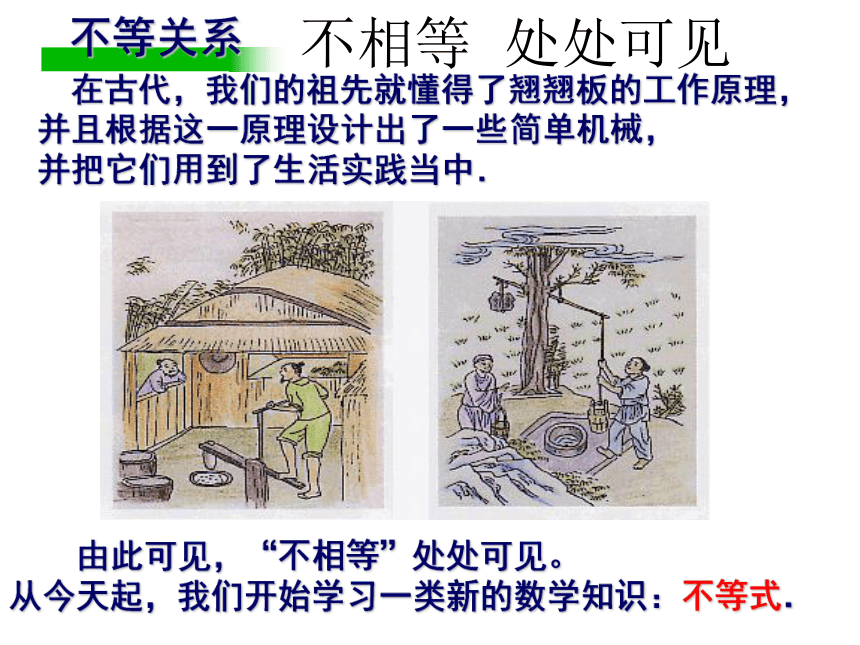
课件31张PPT。§8.1 不等式及其基本性质　在古代，我们的祖先就懂得了翘翘板的工作原理，并且根据这一原理设计出了一些简单机械，
并把它们用到了生活实践当中． 由此可见，“不相等”处处可见。
从今天起，我们开始学习一类新的数学知识：不等式．不相等 处处可见不等关系问题1：用适当的符号表示下列关系：
（1） 与3的和不大于6；
（2） 的5倍与1的差小于 的3倍；
（3）a与b的差是负数。
2x+3≤6a-b<05x-1<3x不等式的定义用不等号（＞、≥、＜、≤或≠）表示不等关系的式子叫做不等式注：不大于，即小于或等于，用“≤”表示；
不小于，即大于或等于，用“≥”表示。如以上的2x+3≤6，a-b<0等都是不等式。
判断下列式子是不是不等式：（1）-3<0; （2）4x+3y>0
（3）x=3;（4） X2+xy+y2
（5）x≠5; （6）X+2>y+5;
不等式的性质思考一下等式具有那些性质？
不等式是否具有这些类似性质？ 等式基本性质1：
等式的两边都加上（或减去）同一个整式，等式仍旧成立等式基本性质2：
等式的两边都乘以（或除以）同一个不为0的数，等式仍旧成立如果a=b,那么a±c=b±c如果a=b,那么ac=bc或 （c≠0），等式基本性质3（对称性）如果a=b，那么b=a。等式基本性质4（传递性）如果a=b,b=c那么a=c不等式是否具有类似的性质呢？如果 7 ＞ 3那么 7+5 ____ 3+ 5 , 7 -5____3-5你能总结一下规律吗？＞＞如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4<<不等式基本性质1：不等式的两边都加上（或减去）同一数或同一个整式，即：如果____,那么_______. 不等号的方向不变。a>ba±c>b±c_______________ 7÷5 ____ 3÷ 5 ,
7 ÷ (-5)____3÷ (-5)不等式还有什么类似的性质呢？已知 7 ＞ 3那么 7×5 ____ 3× 5 ,
7 ×(-5)____3×(-5),你能再总结一下规律吗？＞＞已知-1< 3,
那么-1×2____3×2,
-1×(- 4)____3×( - 4),-1÷2____3÷2,
-1÷ (- 4)____3÷ ( - 4)＞＞<<<<———————————————————————————————————————————————————————————————————————————————- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 不等式基本性质2：不等式的两边都乘以（或除以）同一个____，不等号的方向____。不等式基本性质3：不等式的两边都乘以（或除以）同一个____，不等号的方向____。如果________,那么______________不变正数a>b，c>0ac>bc (或 )负数改变如果________,那么______________a>b，c<0ac5,那么55 ? 5b,那么bb,b>c,那么a>c今天学的是不等式的五个基本性质：不等式的基本性质1：
如果a ＞b，那么a±c＞b±c.就是说，不等式两边都加上 (或减去）同一个数(或同一整式),不等号方向不变。
不等式基本性质2：
如果a ＞b，c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。不等式的对称性：
如果a>b，那么b 如果a>b，b>c,那么a>c不等式基本性质3：
如果a>b，c<0 那么ac （2）a÷3____b÷3
（3） 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6) (m2+1) a ____ (m2+1)b (m为常数)＞＞＞＞＞＜基本性质1基本性质2基本性质2基本性质2、1基本性质3基本性质2例2：判断下列各题的推导是否正确？为什么(学生口答)
(1)因为7.5＞5.7，所以-7.5＜-5.7；
(2)因为a+8＞4，所以a＞-4；
(3)因为4a＞4b，所以a＞b；
(4)因为-1＞-2，所以-a-1＞-a-2；
(5)因为3＞2，所以3a＞2a．
答：(1)正确，根据不等式基本性质3．(2)正确，根据不等式基本性质1．(3)正确，根据不等式基本性质2．(4)正确，根据不等式基本性质1．(5)不对，应分情况逐一讨论．
当a＞0时，3a＞2a．(不等式基本性质2)
当 a=0时，3a=2a．
当a＜0时，3a＜2a．(不等式基本性质3) 1、若m>n，判断下列不等式是否正确：
（1）m-7（2）3m<3n （ ）
（3）-5m>-5n （ ）
（4） ( )
（5） m+5≥n+5 ( )下列是由a"连接.填一填(1)a-1 b-1;
(2)-a -b;
(3)-a+1 -b+1;
(4)2a-1 2b-1. <><>(1)x(2)若-5a<-5b,则a(3)若-a>-b,则2-a>2-b; ( )
(4)若a>b,则ac2>bc2; ( )
(5)若ac2>bc2,则a>b; ( ) (6)若a>0,且(b-1)a<0,则b>1. ( )辩一辩√×√√××例2：将下列不等式化成 X > a或 x < a的形式(1) x-5 -1(2) -2x 3(3) 7x 6x -6＞＞＜不等式的基本性质有什么用呢?(1) x-5 -1＞解：根据不等式的基本性质__，两边都_____，得x＞-1+5即x＞41加上5解：根据不等式的基本性质___，两边都______，得(2) -2x 3＞3除以-2(3) 7x 6x -6＜解：根据不等式的基本性质__，两边都_______，得 7x- 6x < -6即x< -61减去6x知识拓展:(1) ∵ 2a < 3a , ∴a是____数(3) ∵ ax < a 且 x > 1 ,
∴a是____数(2) ∵ , ∴a是____数正正负今天学的是不等式的五个基本性质：不等式的基本性质1：
如果a ＞b，那么a±c＞b±c.就是说，不等式两边都加上 (或减去）同一个数(或式子),不等号方向不变。
不等式基本性质2：
如果a ＞b，c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。本课小结：不等式的对称性：
如果a>b，那么b如果a>b，b>c,那么a>c不等式基本性质3：
如果a>b，c<0 那么ac （1） x – 3 < y – 3 （2）- 5 x < - 5 y
（3） - 3 x +2 < - 3 y + 2 （4）- 3 x + 2 > - 3y + 2 3、已知a>b,若a<0,则a2 ab;若a>0,则a2 ab. 4、下列各式分别在什么条件下成立?
(1) a > - a (2) a2 > a补充作业：下课！