13.2三角形全等的条件(SAS)[上学期]
文档属性
| 名称 | 13.2三角形全等的条件(SAS)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-01 17:39:00 | ||
图片预览






文档简介
课件28张PPT。13.2.2 探索三角形全等的条件 (SAS) 1、探索三角形全等的条件之二:
边边边(SAS)。
2、学会尺规法作图:
已知三角形的两边一角,画出该图。
3、学会用SAS原理证明三角形全等
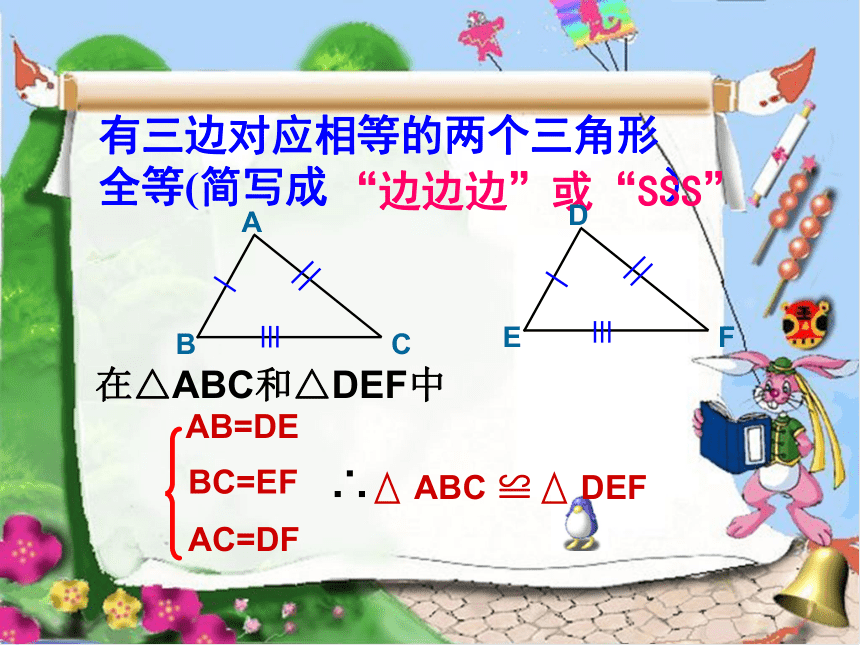
并解决实际问题。本节课学习目标有哪位同学记得我们上节课学习的内容?有三边对应相等的两个三角形全等(简写成 )“边边边”或“SSS”AB=DEBC=EFAC=DF满足三个条件时①三条边对应相等②两边一角对应相等③两角一边对应相等④三个角对应相等思 考探 究 活 动
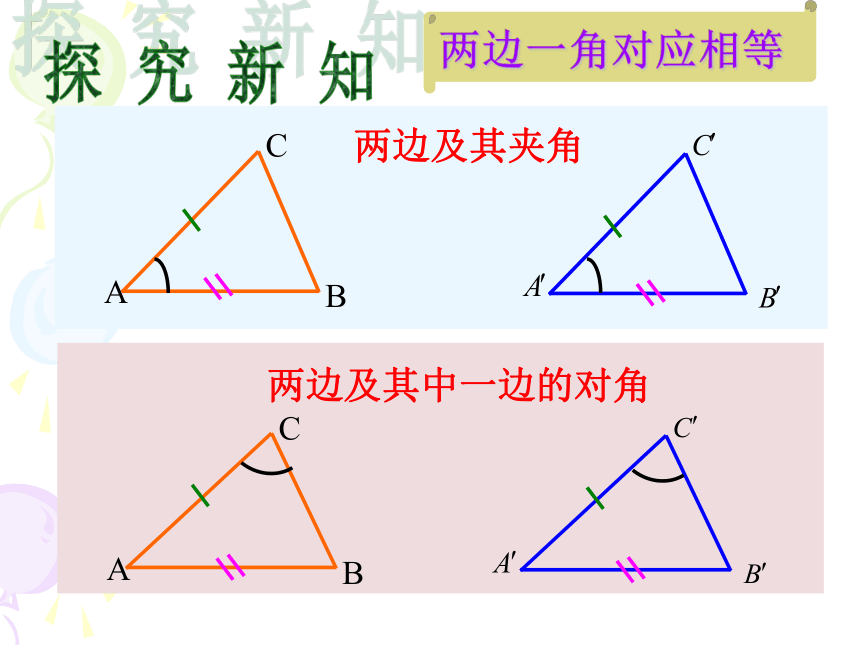
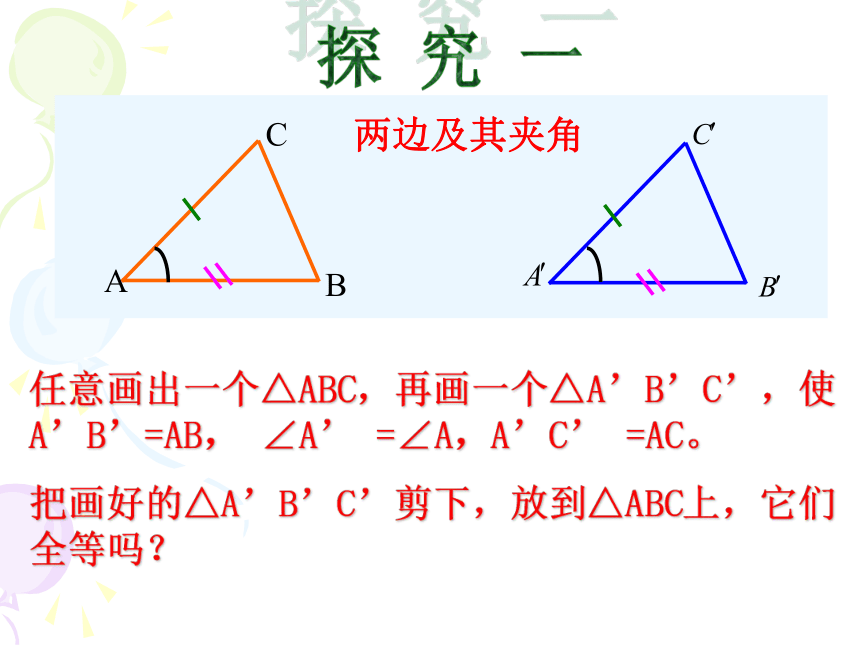
开 始 啦!两边及其夹角两边及其中一边的对角探 究 新 知探 究 一两边及其夹角任意画出一个△ABC,再画一个△A’B’C’,使A’B’=AB, ∠A’ =∠A,A’C’ =AC。
把画好的△A’B’C’剪下,放到△ABC上,它们全等吗?已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC。画法:1、画∠DA’ E=∠A ;2、在射线A’D上截取A’B’=AB,在射线A’ E上截取A’C’=AC;3、连结B’C’。 △A’B’C’就是所要画的三角形。A’画一个三角形,使其两边AC=2.5cm,AB=3.5cm,
它们所夹的角为∠CAB=40° 把你画的三角形剪下来与同伴画的三角形相比,能重合吗?动手画一画!两边和它们的夹角对应相等的两个三角形全等。结 论1 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCD2.5cm3.5cm40°2.5cm结论二:两边及其一边所对的角相等,两个三角形不一定全等探 究 二实 践 得 出两边和它们的夹角对应相等的两个三角形全等。(简写成“边角边”或“SAS”)两边和它们的夹角对应相等的两个三角形全等。(简写成“边角边”或“SAS”)书写格式:在下列图中找出全等三角形。细心找一找例1:如图:如果AB=AC , ∠BAD= ∠CAD。
求证:△ABD≌△ACD。证明:
∵在△ABD与△ACD中,∴ △ABD≌△ACD(SAS)1. 在△ABC和△DEF中AB=DE
_____=______
BC=EF ∴△ABC≌△DEF(SAS)∠B ∠E我 能 行!根据条件,补充下列证明过程。2. 在△ABC和△DEF中 ∴△ABC≌△DEF(SAS)____=____
∠C=∠F
____=____BC EFAC DF我 能 行!3.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSASAD=AD还有其他的补充方案吗?SSSAB=ACBD=CDAD=AD我 能 行!1.在△AOB和△DOC中,已知AO=DO ,BO=CO。
求证: (1)△AOB≌△DOC
(2)AB=DC。你会做吗?∴AB=DC(全等三角形的对应边相等。)2.如图,在△AEC和△ADB中,已知AE=AD,AC=AB。
求证:△AEC ≌ △ADB。例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?ABD CE1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE。在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE ∴△ABD≌△ACE(SAS) ∟ ADBCEFM已知:如图,AB⊥AC,AD⊥AE,
AB=AC,AD=AE. 求证:(1) △DAC≌△EAB
(2) CD=BE
(3) ∠C=∠B
(4)∠D=∠E
(5) ∠ DAC=∠ EAB
课 后 思 考 题说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角、平角等)]
总结:已知中找。图形中看谢谢指导!
边边边(SAS)。
2、学会尺规法作图:
已知三角形的两边一角,画出该图。
3、学会用SAS原理证明三角形全等
并解决实际问题。本节课学习目标有哪位同学记得我们上节课学习的内容?有三边对应相等的两个三角形全等(简写成 )“边边边”或“SSS”AB=DEBC=EFAC=DF满足三个条件时①三条边对应相等②两边一角对应相等③两角一边对应相等④三个角对应相等思 考探 究 活 动
开 始 啦!两边及其夹角两边及其中一边的对角探 究 新 知探 究 一两边及其夹角任意画出一个△ABC,再画一个△A’B’C’,使A’B’=AB, ∠A’ =∠A,A’C’ =AC。
把画好的△A’B’C’剪下,放到△ABC上,它们全等吗?已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, A/C/=AC。画法:1、画∠DA’ E=∠A ;2、在射线A’D上截取A’B’=AB,在射线A’ E上截取A’C’=AC;3、连结B’C’。 △A’B’C’就是所要画的三角形。A’画一个三角形,使其两边AC=2.5cm,AB=3.5cm,
它们所夹的角为∠CAB=40° 把你画的三角形剪下来与同伴画的三角形相比,能重合吗?动手画一画!两边和它们的夹角对应相等的两个三角形全等。结 论1 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCD2.5cm3.5cm40°2.5cm结论二:两边及其一边所对的角相等,两个三角形不一定全等探 究 二实 践 得 出两边和它们的夹角对应相等的两个三角形全等。(简写成“边角边”或“SAS”)两边和它们的夹角对应相等的两个三角形全等。(简写成“边角边”或“SAS”)书写格式:在下列图中找出全等三角形。细心找一找例1:如图:如果AB=AC , ∠BAD= ∠CAD。
求证:△ABD≌△ACD。证明:
∵在△ABD与△ACD中,∴ △ABD≌△ACD(SAS)1. 在△ABC和△DEF中AB=DE
_____=______
BC=EF ∴△ABC≌△DEF(SAS)∠B ∠E我 能 行!根据条件,补充下列证明过程。2. 在△ABC和△DEF中 ∴△ABC≌△DEF(SAS)____=____
∠C=∠F
____=____BC EFAC DF我 能 行!3.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSASAD=AD还有其他的补充方案吗?SSSAB=ACBD=CDAD=AD我 能 行!1.在△AOB和△DOC中,已知AO=DO ,BO=CO。
求证: (1)△AOB≌△DOC
(2)AB=DC。你会做吗?∴AB=DC(全等三角形的对应边相等。)2.如图,在△AEC和△ADB中,已知AE=AD,AC=AB。
求证:△AEC ≌ △ADB。例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?ABD CE1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE。在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE ∴△ABD≌△ACE(SAS) ∟ ADBCEFM已知:如图,AB⊥AC,AD⊥AE,
AB=AC,AD=AE. 求证:(1) △DAC≌△EAB
(2) CD=BE
(3) ∠C=∠B
(4)∠D=∠E
(5) ∠ DAC=∠ EAB
课 后 思 考 题说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等怎样找已知条件:
[一是已知中给出的,二是图形中隐含的(如:公共边 、公共角、对顶角、邻补角,外角、平角等)]
总结:已知中找。图形中看谢谢指导!
