18.2.1 矩形的性质 课件(共36张PPT)
文档属性
| 名称 | 18.2.1 矩形的性质 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 10:00:11 | ||
图片预览








文档简介
(共36张PPT)
18.2.1 矩形的性质
人教版八年级下册
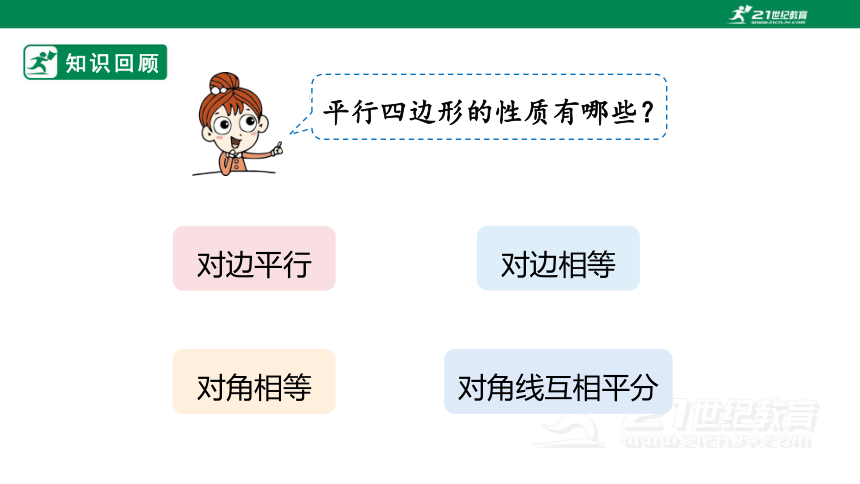
知识回顾
对边平行
对边相等
对角相等
对角线互相平分
平行四边形的性质有哪些?
教学目标
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
新知导入
矩形是生活中常见的图形,你平时有注意到吗?
新知探究
你还注意到生活中有哪些矩形?
新知导入
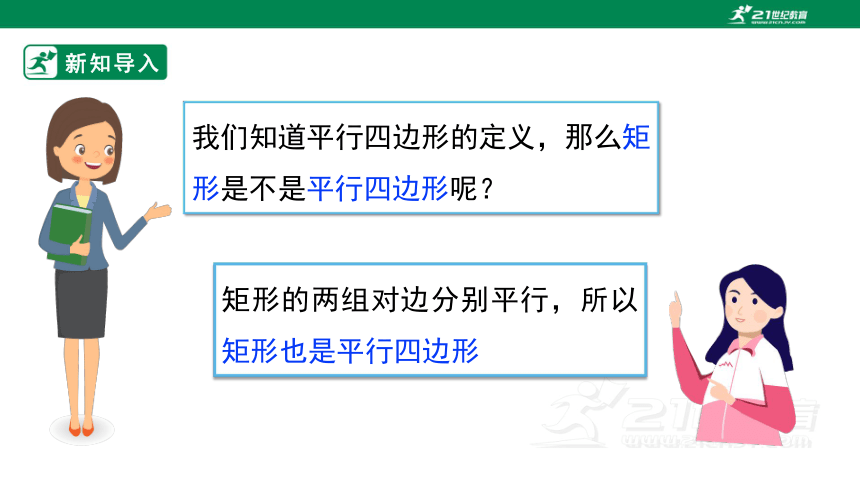
我们知道平行四边形的定义,那么矩形是不是平行四边形呢?
矩形的两组对边分别平行,所以矩形也是平行四边形
新知导入
矩形
由上图的变换,大家想一想矩形的定义?
猜想:有 个角为直角的平行四边形为矩形
四
新知探究
根据平行四边形的性质,只要有一个角为直角,就可以得到其他3个角也是直角了。
A
B
C
D
已知: ABCD中,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
证明:∵平行四边形ABCD中,∠A=90°
∴∠C=∠A=90°,∠B=∠D
AD BC
∴∠A+∠B=180°
∴∠B=90°
∴∠A=∠B=∠C=∠D=90°
新知探究
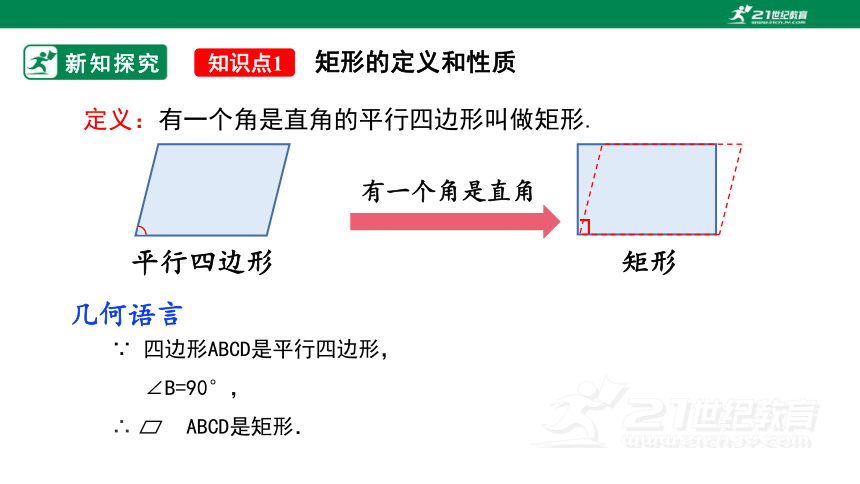
定义:有一个角是直角的平行四边形叫做矩形.
┐
平行四边形
矩形
有一个角是直角
知识点1
矩形的定义和性质
∵ 四边形ABCD是平行四边形,
∠B=90°,
∴ ABCD是矩形.
几何语言
新知探究
矩形是特殊的平行四边形,但平行四边形不一定是矩形.
1. 矩形必须具备两个条件:
①是平行四边形;
②有一个角是直角.两个条件缺一不可.
2. 矩形的定义可以作为判定一个四边形是矩形的方法.
新知探究
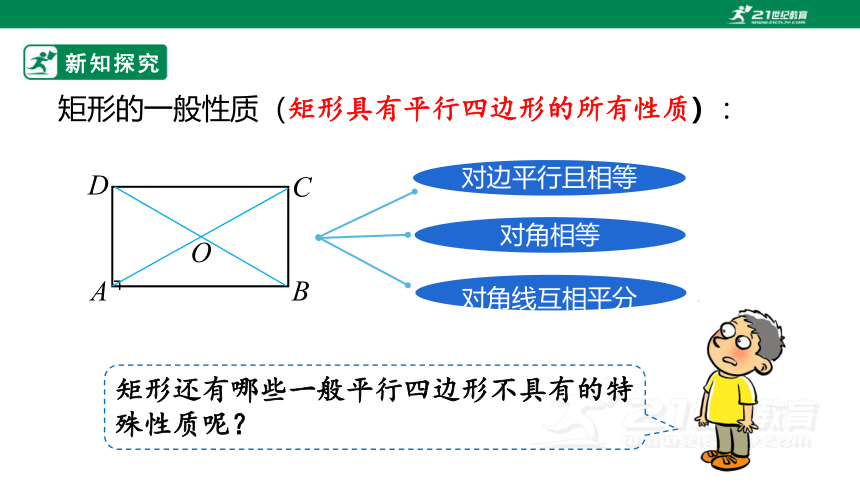
矩形的一般性质(矩形具有平行四边形的所有性质):
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
┐
O
矩形还有哪些一般平行四边形不具有的特殊性质呢?
新知探究
思考1 有一个角是直角的平行四边形是矩形,那么矩形其他的内角都是多少呢?
A
B
D
C
┐
矩形ABCD中, ∠A = 90 .
经过全面的证明,可知∠A =∠B =∠C =∠D = 90 .
矩形的四个角都是直角
新知探究
思考2 平行四边形对角线互相平分,那么矩形的对角线有特殊的性质吗?
矩形ABCD中,∠A=∠B=∠C
=∠D = 90 .
猜想:AC=BD.
A
B
D
C
┐
新知探究
如图,矩形ABCD中,求证: AC=BD.
证明:∵四边形ABCD是矩形
∴∠DAB=∠ABC=∠BCD=∠CDA=90 ,AD=BC
∵ AB是△DAB和△CBA的公共边
∴ △DAB≌△CBA(SAS)
∴ AC=BD.
A
B
D
C
┐
矩形的对角线相等
新知小结
矩形 性质
边
角
对角线
矩形是特殊的平行四边形
对边平行且相等
四个角都是直角
对角线相等且互相平分
新知小结
边
角
对角线
对边平行且相等
四个角都是直角
对角线相等且互相平分
性质
矩形
角特殊化
一般
特殊
A
B
D
C
平行四边形
新知探究
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
对角线相等且互相平分
分析:
(等边三角形)
等腰三角形
矩形的性质
新知探究
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
OA=AB=4
OA=OB=OC=OD
△AOB是等边三角形
四边形ABCD是矩形
AC=8
分析:
新知探究
四个角都是直角
分析:
直角三角形
矩形的性质
勾股定理
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
新知探究
BC
∠ABC=∠DCB=∠CDA=∠DAB=90°
分析:
△ABC是直角三角形
四边形ABCD是矩形
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
新知探究
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD =BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
∵ ∠ABC=90°,
∴ △ABC是直角三角形.
在Rt△ABC中,,
∴ .
新知小结
等腰三角形
直角三角形
等边三角形
含30°角的直角三角形
A
B
C
D
O
60°
例题小结
30°
新知练习
如图,在矩形ABCD中, E是BC上一点, AE=AD, DF⊥
AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连结DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,∴△DFE≌△DCE(AAS),
∴DF=DC.
1.
新知探究
A
B
D
C
┐
矩形是轴对称图形吗?如果是,它有几条对称轴呢?
是.它有两条对称轴,分别是对边中点连线所在的直线.
新知探究
知识点2
直角三角形斜边上中线的性质
思考 如图,矩形ABCD的对角线AC、BD相交于点O. 我们观察Rt△ABC, 在Rt△ABC中, BO是斜边AC上的中线,BO 与AC 有什么关系?
A
B
D
C
┐
O
新知探究
如图,矩形ABCD的对角线AC、BD相交于点O. 试判断,在Rt△ABC中,BO与AC的关系.
解:∵四边形ABCD是矩形
∴
∴
A
B
D
C
┐
O
新知探究
性质 直角三角形斜边上的中线等于斜边的一半.
该性质的逆命题“如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形”仍然成立,它可以用来判断一个三角形是否为直角三角形.
拓展
新知练习
如图,在Rt△ABC中, ∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线, AD=2, CE=5,则CD=( ).
A.2 B.3 C.4 D.
解析: ∵在Rt△ABC中, ∠ACB=90 ,
CE为AB边上的中线, CE=5
∴AE=CE=5
∵AD=2
∴DE=3
∵CD为AB边上的高
∴在Rt△CDE中,
C
课堂总结
矩形
概念
特殊性质
有一个角是直角的平行四边形是矩形.
①四个角都是直角
②对角线相等
③轴对称图形
直角三角形斜边上的中线等于斜边的一半.
课堂练习
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ADB=34°,则∠BAO的度数是( )
A.46° B.54°
C.56° D.60°
C
B
C
A
D
O
34°
34°
56°
课堂练习
2. 矩形 ABCD 中,对角线 AC、BD 相交于点 O,请填写下列空格.
(1)若OA=4,则BD= .
8
(2)若∠DAO=60 , AD=3,则
AC= .
6
A
B
D
C
O
课堂练习
3.如图,在△ABC中,AD是高,E、F分别是边AB、AC的中点.
若AB=10,AC=8,求四边形AEDF的周长;
解:∵AD是△ABC的高,E、F分别是
边AB、AC的中点,
∴DE=AE= AB= ×10=5,
DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18.
课堂练习
4.如图,矩形 ABCD 中,E 为 AD 上一点, EF⊥CE 交AB 于点 F,若 DE=2,矩形 ABCD 的周长为 16,且CE=EF,求 AE 的长.
解:∵四边形 ABCD 为矩形
B
C
A
D
┐
E
F
∴ ∠A=∠D=90
∵EF⊥CE
∴ ∠AEF+∠DEC=90
∵ ∠A=90
∴ ∠AEF+∠AFE=90
∴ ∠DEC=∠AFE
课堂练习
∵ 在△AEF 和△DCE 中,∠A=∠D=90 ,∠AFE=∠DEC,EF=CE
∴△AEF≌△DCE(AAS),AE=DC
∵ 矩形 ABCD 的周长为16
∴ AD+CD=8
∵ DE=2,AE=DC ∴ 2+AE+AE=8
∴ AE=3
B
C
A
D
┐
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.2.1 矩形的性质
人教版八年级下册
知识回顾
对边平行
对边相等
对角相等
对角线互相平分
平行四边形的性质有哪些?
教学目标
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
新知导入
矩形是生活中常见的图形,你平时有注意到吗?
新知探究
你还注意到生活中有哪些矩形?
新知导入
我们知道平行四边形的定义,那么矩形是不是平行四边形呢?
矩形的两组对边分别平行,所以矩形也是平行四边形
新知导入
矩形
由上图的变换,大家想一想矩形的定义?
猜想:有 个角为直角的平行四边形为矩形
四
新知探究
根据平行四边形的性质,只要有一个角为直角,就可以得到其他3个角也是直角了。
A
B
C
D
已知: ABCD中,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
证明:∵平行四边形ABCD中,∠A=90°
∴∠C=∠A=90°,∠B=∠D
AD BC
∴∠A+∠B=180°
∴∠B=90°
∴∠A=∠B=∠C=∠D=90°
新知探究
定义:有一个角是直角的平行四边形叫做矩形.
┐
平行四边形
矩形
有一个角是直角
知识点1
矩形的定义和性质
∵ 四边形ABCD是平行四边形,
∠B=90°,
∴ ABCD是矩形.
几何语言
新知探究
矩形是特殊的平行四边形,但平行四边形不一定是矩形.
1. 矩形必须具备两个条件:
①是平行四边形;
②有一个角是直角.两个条件缺一不可.
2. 矩形的定义可以作为判定一个四边形是矩形的方法.
新知探究
矩形的一般性质(矩形具有平行四边形的所有性质):
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
┐
O
矩形还有哪些一般平行四边形不具有的特殊性质呢?
新知探究
思考1 有一个角是直角的平行四边形是矩形,那么矩形其他的内角都是多少呢?
A
B
D
C
┐
矩形ABCD中, ∠A = 90 .
经过全面的证明,可知∠A =∠B =∠C =∠D = 90 .
矩形的四个角都是直角
新知探究
思考2 平行四边形对角线互相平分,那么矩形的对角线有特殊的性质吗?
矩形ABCD中,∠A=∠B=∠C
=∠D = 90 .
猜想:AC=BD.
A
B
D
C
┐
新知探究
如图,矩形ABCD中,求证: AC=BD.
证明:∵四边形ABCD是矩形
∴∠DAB=∠ABC=∠BCD=∠CDA=90 ,AD=BC
∵ AB是△DAB和△CBA的公共边
∴ △DAB≌△CBA(SAS)
∴ AC=BD.
A
B
D
C
┐
矩形的对角线相等
新知小结
矩形 性质
边
角
对角线
矩形是特殊的平行四边形
对边平行且相等
四个角都是直角
对角线相等且互相平分
新知小结
边
角
对角线
对边平行且相等
四个角都是直角
对角线相等且互相平分
性质
矩形
角特殊化
一般
特殊
A
B
D
C
平行四边形
新知探究
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
对角线相等且互相平分
分析:
(等边三角形)
等腰三角形
矩形的性质
新知探究
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
OA=AB=4
OA=OB=OC=OD
△AOB是等边三角形
四边形ABCD是矩形
AC=8
分析:
新知探究
四个角都是直角
分析:
直角三角形
矩形的性质
勾股定理
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
新知探究
BC
∠ABC=∠DCB=∠CDA=∠DAB=90°
分析:
△ABC是直角三角形
四边形ABCD是矩形
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
新知探究
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD =BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
A
B
C
D
O
∵ ∠ABC=90°,
∴ △ABC是直角三角形.
在Rt△ABC中,,
∴ .
新知小结
等腰三角形
直角三角形
等边三角形
含30°角的直角三角形
A
B
C
D
O
60°
例题小结
30°
新知练习
如图,在矩形ABCD中, E是BC上一点, AE=AD, DF⊥
AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连结DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,∴△DFE≌△DCE(AAS),
∴DF=DC.
1.
新知探究
A
B
D
C
┐
矩形是轴对称图形吗?如果是,它有几条对称轴呢?
是.它有两条对称轴,分别是对边中点连线所在的直线.
新知探究
知识点2
直角三角形斜边上中线的性质
思考 如图,矩形ABCD的对角线AC、BD相交于点O. 我们观察Rt△ABC, 在Rt△ABC中, BO是斜边AC上的中线,BO 与AC 有什么关系?
A
B
D
C
┐
O
新知探究
如图,矩形ABCD的对角线AC、BD相交于点O. 试判断,在Rt△ABC中,BO与AC的关系.
解:∵四边形ABCD是矩形
∴
∴
A
B
D
C
┐
O
新知探究
性质 直角三角形斜边上的中线等于斜边的一半.
该性质的逆命题“如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形”仍然成立,它可以用来判断一个三角形是否为直角三角形.
拓展
新知练习
如图,在Rt△ABC中, ∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线, AD=2, CE=5,则CD=( ).
A.2 B.3 C.4 D.
解析: ∵在Rt△ABC中, ∠ACB=90 ,
CE为AB边上的中线, CE=5
∴AE=CE=5
∵AD=2
∴DE=3
∵CD为AB边上的高
∴在Rt△CDE中,
C
课堂总结
矩形
概念
特殊性质
有一个角是直角的平行四边形是矩形.
①四个角都是直角
②对角线相等
③轴对称图形
直角三角形斜边上的中线等于斜边的一半.
课堂练习
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ADB=34°,则∠BAO的度数是( )
A.46° B.54°
C.56° D.60°
C
B
C
A
D
O
34°
34°
56°
课堂练习
2. 矩形 ABCD 中,对角线 AC、BD 相交于点 O,请填写下列空格.
(1)若OA=4,则BD= .
8
(2)若∠DAO=60 , AD=3,则
AC= .
6
A
B
D
C
O
课堂练习
3.如图,在△ABC中,AD是高,E、F分别是边AB、AC的中点.
若AB=10,AC=8,求四边形AEDF的周长;
解:∵AD是△ABC的高,E、F分别是
边AB、AC的中点,
∴DE=AE= AB= ×10=5,
DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18.
课堂练习
4.如图,矩形 ABCD 中,E 为 AD 上一点, EF⊥CE 交AB 于点 F,若 DE=2,矩形 ABCD 的周长为 16,且CE=EF,求 AE 的长.
解:∵四边形 ABCD 为矩形
B
C
A
D
┐
E
F
∴ ∠A=∠D=90
∵EF⊥CE
∴ ∠AEF+∠DEC=90
∵ ∠A=90
∴ ∠AEF+∠AFE=90
∴ ∠DEC=∠AFE
课堂练习
∵ 在△AEF 和△DCE 中,∠A=∠D=90 ,∠AFE=∠DEC,EF=CE
∴△AEF≌△DCE(AAS),AE=DC
∵ 矩形 ABCD 的周长为16
∴ AD+CD=8
∵ DE=2,AE=DC ∴ 2+AE+AE=8
∴ AE=3
B
C
A
D
┐
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
