《同步测控全优设计》2013-2014学年沪科版八年级数学下册单元检测:第18章 勾股定理(含答案解析)
文档属性
| 名称 | 《同步测控全优设计》2013-2014学年沪科版八年级数学下册单元检测:第18章 勾股定理(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-10 00:00:00 | ||
图片预览


文档简介
数学沪科八年级下第18章 勾股定理单元检测
(时间:60分钟 分值:100分)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项正确)
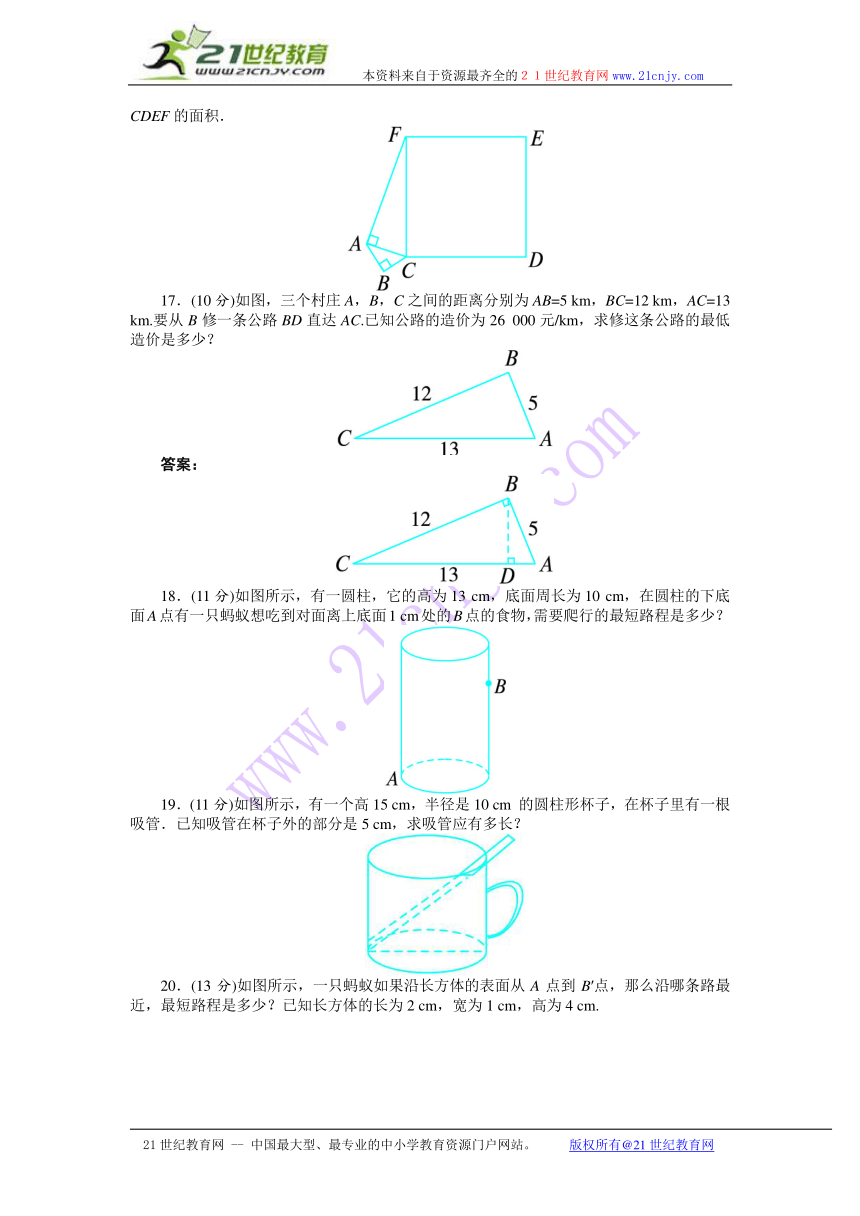
1.图中,每个小正方形的边长为1,△ABC的三边a,b,c的大小关系是( ).
A.a<c<b B.a<b<c21世纪教育网
C.c<a<b D.c<b<a
2.如果等腰三角形的底角为30°,腰长为6 cm,那么这个三角形的面积为( ).
A.4.5 cm2 B.
C. D.36 cm2
3.如图,正方形网格中,每个小正方形的边长都为1,则在网格上的△ABC中,边长为无理数的边数有( ).21教育网
A.0条 B.1条 C.2条 D.3条
4.已知如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕A逆时针旋转后,能够与△ACP′重合,如果AP=3,那么PP′2的长等于( ).www.21-cn-jy.com
A.9 B.12 C.15 D.18
5.已知,如图,AB⊥CD,△ABD,△ BCE都是等腰三角形,如果CD=7,BE=3,那么AC的长为( ).21·世纪*教育网
A.8 B.5 C.3 D.4
6.若三角形三个内角度数之比为1∶2∶3,则此三角形三个内角的对边之比为( ).
A.1∶2∶3 B.3∶2∶1
C. D.无法确定
7.直角三角形中,以直角边为边长的两个正方形的面积分别为36和64,那么以斜边为边长的正方形的面积是( ).www-2-1-cnjy-com
A.54 B.100 C.72 D.120
8.下列命题中是假命题的是( ).[来源:21世纪教育网]
A.△ ABC中,若∠A=∠C-∠B,则△ABC是直角三角形
B.△ABC中,若a2=b2-c2,则△ABC是直角三角形
C.△ABC中,若∠A,∠B,∠C的度数比是5∶2∶3,则△ABC是直角三角形
D.△ABC中,若a∶b∶c=2∶2∶3,则△ABC是直角三角形
9.直角三角形的一直角边长为12,另外两边长为自然数,则满足条件的直角三角形共有( ).
A.4个 B.5个 C.6个 D.8个21世纪教育网
10.一正方形的面积为,则其对角线AC的长度为( ).
A. B. C. D.
二、填空题(本题共5小题,每小题3分,共15分)
11.在△ABC中,∠C=90°,若b=15,c=20,则a=__________.
12.木工做一个长方形桌面,量得桌面的长为60 cm,宽为32 cm,对角线长为68 cm,则这个桌面__________(填“合格”或“不合格”).21世纪教育网版权所有
13.如图,某人在点B处,通过平面镜看见在B处正上方3 m处的A物体,已知物体A到平面镜的距离为2 m,则B点到物体A的像A′的距离为__________.
14.把命题 “如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2”的逆命题写成“如果……,那么……”的形式:______________.
15.如图,在等腰△ABC中,∠C=90°,BC=2 cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B若在B′处,那么点B′与点B的距离为__________.
三、计算题(共55分,要求写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不能给分)
16.(10分)如图所示,BC长为3厘米,AB长为4厘米,AF长为12厘米,求正方形CDEF的面积.21cnjy.com
17.(10分)如图,三个村庄A,B,C之间的距离分别为AB=5 km,BC=12 km,AC=13 km.要从B修一条公路BD直达AC.已知公路的造价为26 000元/km,求修这条公路的最低造价是多少?2-1-c-n-j-y
答案:
18.(11分)如图所示,有一圆柱,它的高为13 cm,底面周长为10 cm,在圆柱的下底面A点有一只蚂蚁想吃到对面离上底面1 cm处的B点的食物,需要爬行的最短路程是多少?
19.(11分)如图所示,有一个高15 cm,半径是10 cm 的圆柱形杯子,在杯子里有一根吸管.已知吸管在杯子外的部分是5 cm,求吸管应有多长? 21*cnjy*com
20.(13分)如图所示,一只蚂蚁如果沿长方体的表面从A点到B′点,那么沿哪条路最近,最短路程是多少?已知长方体的长为2 cm,宽为1 cm,高为4 cm.
参考答案
1. 答案:C 点拨:根据勾股定理可以求出AC=5,,AB=4,所以.即c<a<b.故选C.
2. 答案:B
3. 答案:C
4. 答案:D 点拨:△ABP≌△ACP′,AP=AP′,
在Rt△APP′中,PP′2=AP2+AP′2=32+32=18.
5. 答案:B 点拨:已知条件,知BC=BE=3,BD=AB=4,由勾股定理可求出AC=5.
6. 答案:C
7. 答案:B
8. 答案:D
9. 答案:A
10. 答案:A 点拨:正方形的面积为,所以其边长的平方是,对角线AC的长的平方等于,所以,故选A.2·1·c·n·j·y
11. 答案:
12. 答案:合格
13. 答案:5 m 点拨:在Rt△AA′B中,AA′=2+2=4(m),AB=3 m,
∴.
14. 答案:如果三角形的三边长分别为a,b,c,且满足a2+b2=c2,那么这个三角形是直角三角形.【来源:21·世纪·教育·网】
15. 答案:
16. 解:在Rt△ABC中,
AC2=AB2+BC2=42+32=25,
在Rt△ACF中,
FC2=AF2+AC2=122+25=169,[21世纪教育网
所以S正方形CDEF=FC2=169(厘米2).
17. 解:∵52+122=132,∴AB2+BC2=AC2.
∴△ABC是直角三角形,过点B作BD⊥AC,垂足为D.
∴BD·CA=BC·BA.
∴.
∴最低造价为.21世纪教育网
18. 解:如图,需爬行的最短路程是线段AB的长.
∵AC=5 cm,BC=13-1=12(cm),
∴AB2=AC2+BC2=52+122=132.
∴AB=13 cm.
故需要爬行的最短路程为13 cm.
19. 解:设吸管在杯子里面的部分长为x cm,
则有x2=152+(10×2)2=252,∴x=25.
25+5=30(cm).
答:吸管总长为30 cm.
20. 解:根据题意,如图所示,路径有下列三种情况:
(1)沿AC,BC,AA′,A′C′,C′B′,BB′剪开,得图(1).AB′2=AB2+B′B2=(2+1)2+42=32+42=25.21·cn·jy·com
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2).
AB′2=AC2+CB′2=22+(4+1)2=22+52=29.
(3)沿AD,DD′,B′D′,C′B′,C′A′,A′A剪开,得图(3).
AB′2=AD2+B′D2=12+(2+4)2=12+62=37.
综上所述,最短路径应为图(1)所示.
∴AB′2=25,即AB′=5 cm.
答:最短路径为5 cm,如图(1)所示.
(时间:60分钟 分值:100分)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项正确)
1.图中,每个小正方形的边长为1,△ABC的三边a,b,c的大小关系是( ).
A.a<c<b B.a<b<c21世纪教育网
C.c<a<b D.c<b<a
2.如果等腰三角形的底角为30°,腰长为6 cm,那么这个三角形的面积为( ).
A.4.5 cm2 B.
C. D.36 cm2
3.如图,正方形网格中,每个小正方形的边长都为1,则在网格上的△ABC中,边长为无理数的边数有( ).21教育网
A.0条 B.1条 C.2条 D.3条
4.已知如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕A逆时针旋转后,能够与△ACP′重合,如果AP=3,那么PP′2的长等于( ).www.21-cn-jy.com
A.9 B.12 C.15 D.18
5.已知,如图,AB⊥CD,△ABD,△ BCE都是等腰三角形,如果CD=7,BE=3,那么AC的长为( ).21·世纪*教育网
A.8 B.5 C.3 D.4
6.若三角形三个内角度数之比为1∶2∶3,则此三角形三个内角的对边之比为( ).
A.1∶2∶3 B.3∶2∶1
C. D.无法确定
7.直角三角形中,以直角边为边长的两个正方形的面积分别为36和64,那么以斜边为边长的正方形的面积是( ).www-2-1-cnjy-com
A.54 B.100 C.72 D.120
8.下列命题中是假命题的是( ).[来源:21世纪教育网]
A.△ ABC中,若∠A=∠C-∠B,则△ABC是直角三角形
B.△ABC中,若a2=b2-c2,则△ABC是直角三角形
C.△ABC中,若∠A,∠B,∠C的度数比是5∶2∶3,则△ABC是直角三角形
D.△ABC中,若a∶b∶c=2∶2∶3,则△ABC是直角三角形
9.直角三角形的一直角边长为12,另外两边长为自然数,则满足条件的直角三角形共有( ).
A.4个 B.5个 C.6个 D.8个21世纪教育网
10.一正方形的面积为,则其对角线AC的长度为( ).
A. B. C. D.
二、填空题(本题共5小题,每小题3分,共15分)
11.在△ABC中,∠C=90°,若b=15,c=20,则a=__________.
12.木工做一个长方形桌面,量得桌面的长为60 cm,宽为32 cm,对角线长为68 cm,则这个桌面__________(填“合格”或“不合格”).21世纪教育网版权所有
13.如图,某人在点B处,通过平面镜看见在B处正上方3 m处的A物体,已知物体A到平面镜的距离为2 m,则B点到物体A的像A′的距离为__________.
14.把命题 “如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2”的逆命题写成“如果……,那么……”的形式:______________.
15.如图,在等腰△ABC中,∠C=90°,BC=2 cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B若在B′处,那么点B′与点B的距离为__________.
三、计算题(共55分,要求写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不能给分)
16.(10分)如图所示,BC长为3厘米,AB长为4厘米,AF长为12厘米,求正方形CDEF的面积.21cnjy.com
17.(10分)如图,三个村庄A,B,C之间的距离分别为AB=5 km,BC=12 km,AC=13 km.要从B修一条公路BD直达AC.已知公路的造价为26 000元/km,求修这条公路的最低造价是多少?2-1-c-n-j-y
答案:
18.(11分)如图所示,有一圆柱,它的高为13 cm,底面周长为10 cm,在圆柱的下底面A点有一只蚂蚁想吃到对面离上底面1 cm处的B点的食物,需要爬行的最短路程是多少?
19.(11分)如图所示,有一个高15 cm,半径是10 cm 的圆柱形杯子,在杯子里有一根吸管.已知吸管在杯子外的部分是5 cm,求吸管应有多长? 21*cnjy*com
20.(13分)如图所示,一只蚂蚁如果沿长方体的表面从A点到B′点,那么沿哪条路最近,最短路程是多少?已知长方体的长为2 cm,宽为1 cm,高为4 cm.
参考答案
1. 答案:C 点拨:根据勾股定理可以求出AC=5,,AB=4,所以.即c<a<b.故选C.
2. 答案:B
3. 答案:C
4. 答案:D 点拨:△ABP≌△ACP′,AP=AP′,
在Rt△APP′中,PP′2=AP2+AP′2=32+32=18.
5. 答案:B 点拨:已知条件,知BC=BE=3,BD=AB=4,由勾股定理可求出AC=5.
6. 答案:C
7. 答案:B
8. 答案:D
9. 答案:A
10. 答案:A 点拨:正方形的面积为,所以其边长的平方是,对角线AC的长的平方等于,所以,故选A.2·1·c·n·j·y
11. 答案:
12. 答案:合格
13. 答案:5 m 点拨:在Rt△AA′B中,AA′=2+2=4(m),AB=3 m,
∴.
14. 答案:如果三角形的三边长分别为a,b,c,且满足a2+b2=c2,那么这个三角形是直角三角形.【来源:21·世纪·教育·网】
15. 答案:
16. 解:在Rt△ABC中,
AC2=AB2+BC2=42+32=25,
在Rt△ACF中,
FC2=AF2+AC2=122+25=169,[21世纪教育网
所以S正方形CDEF=FC2=169(厘米2).
17. 解:∵52+122=132,∴AB2+BC2=AC2.
∴△ABC是直角三角形,过点B作BD⊥AC,垂足为D.
∴BD·CA=BC·BA.
∴.
∴最低造价为.21世纪教育网
18. 解:如图,需爬行的最短路程是线段AB的长.
∵AC=5 cm,BC=13-1=12(cm),
∴AB2=AC2+BC2=52+122=132.
∴AB=13 cm.
故需要爬行的最短路程为13 cm.
19. 解:设吸管在杯子里面的部分长为x cm,
则有x2=152+(10×2)2=252,∴x=25.
25+5=30(cm).
答:吸管总长为30 cm.
20. 解:根据题意,如图所示,路径有下列三种情况:
(1)沿AC,BC,AA′,A′C′,C′B′,BB′剪开,得图(1).AB′2=AB2+B′B2=(2+1)2+42=32+42=25.21·cn·jy·com
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2).
AB′2=AC2+CB′2=22+(4+1)2=22+52=29.
(3)沿AD,DD′,B′D′,C′B′,C′A′,A′A剪开,得图(3).
AB′2=AD2+B′D2=12+(2+4)2=12+62=37.
综上所述,最短路径应为图(1)所示.
∴AB′2=25,即AB′=5 cm.
答:最短路径为5 cm,如图(1)所示.
