等腰三角形[上学期]
图片预览

文档简介
课件14张PPT。等腰三角形ABC等腰三角形的定义:
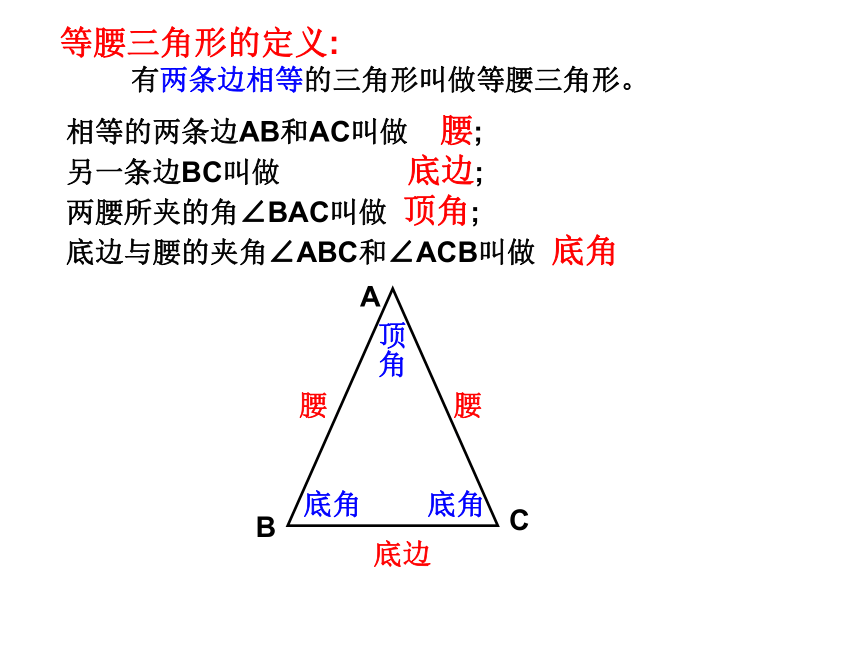
有两条边相等的三角形叫做等腰三角形。相等的两条边AB和AC叫做 腰;
另一条边BC叫做 底边;
两腰所夹的角∠BAC叫做 顶角;
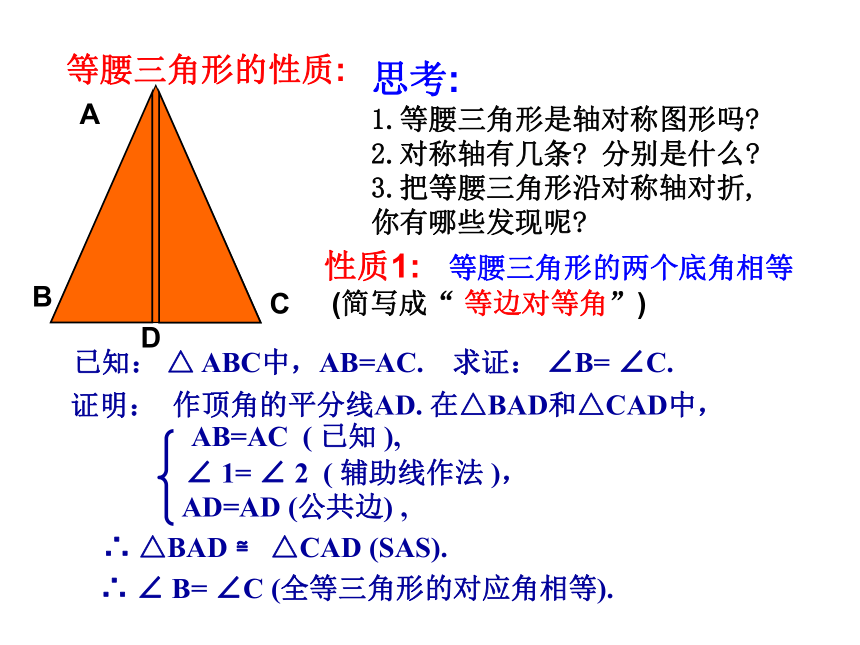
底边与腰的夹角∠ABC和∠ACB叫做 底角底角底角腰腰底边顶角ABCD等腰三角形的性质: 性质1: 等腰三角形的两个底角相等
(简写成“ 等边对等角”)思考:
1.等腰三角形是轴对称图形吗?
2.对称轴有几条? 分别是什么?
3.把等腰三角形沿对称轴对折,你有哪些发现呢?已知: △ ABC中,AB=AC. 求证: ∠B= ∠C.证明:作顶角的平分线AD. 在△BAD和△CAD中,AB=AC ( 已知 ),∠ 1= ∠ 2 ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).1.已知AB=AC,则两底角∠B与∠C关系怎么样?
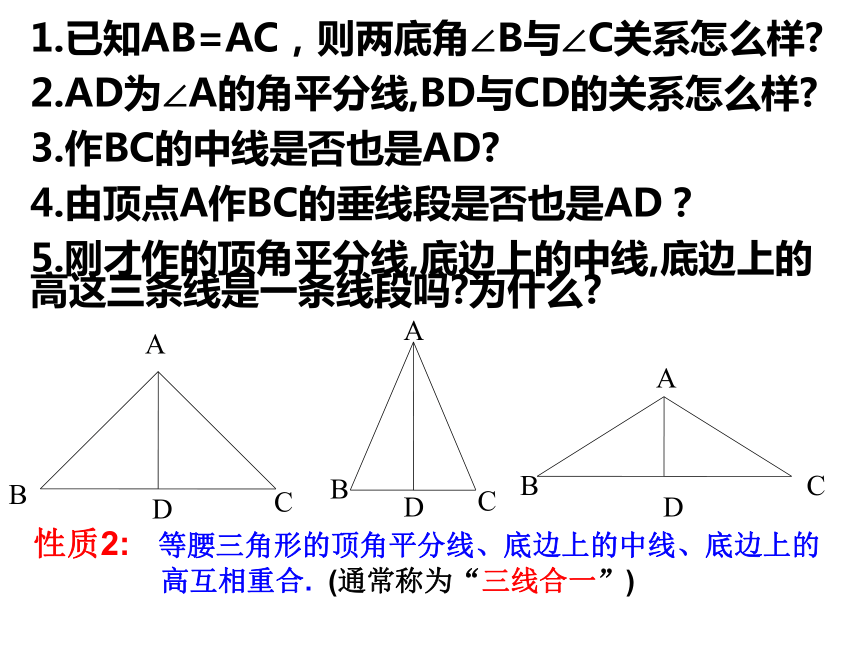
2.AD为∠A的角平分线,BD与CD的关系怎么样?
3.作BC的中线是否也是AD?
4.由顶点A作BC的垂线段是否也是AD?
5.刚才作的顶角平分线,底边上的中线,底边上的高这三条线是一条线段吗?为什么? 性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的
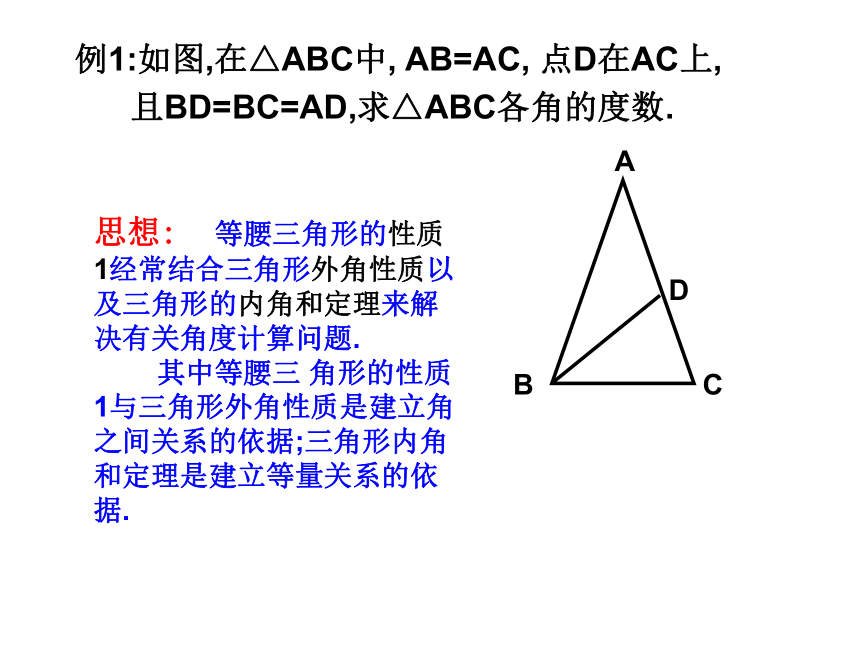
高互相重合. (通常称为“三线合一”)B例1:如图,在△ABC中, AB=AC, 点D在AC上,
且BD=BC=AD,求△ABC各角的度数.思想: 等腰三角形的性质1经常结合三角形外角性质以及三角形的内角和定理来解决有关角度计算问题.
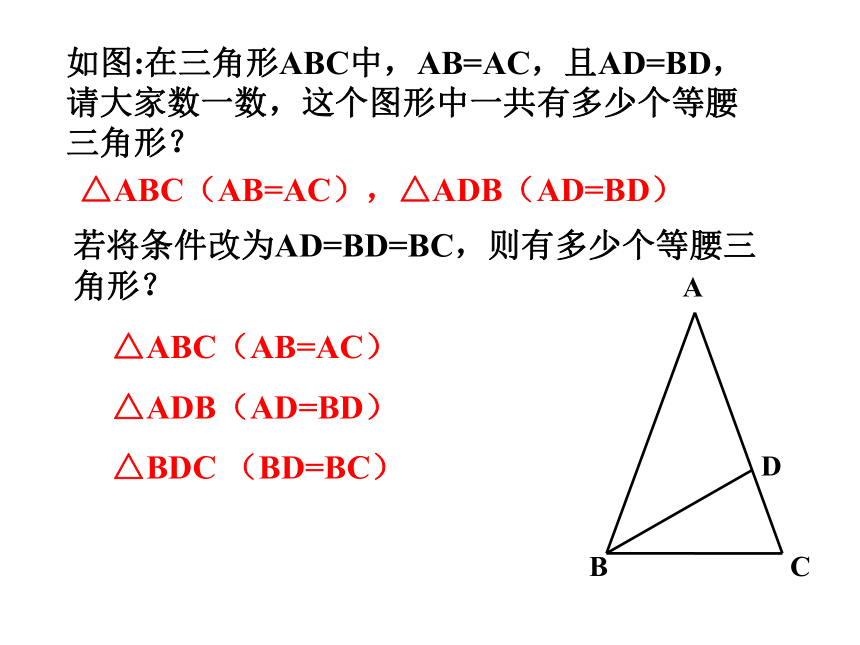
其中等腰三 角形的性质1与三角形外角性质是建立角之间关系的依据;三角形内角和定理是建立等量关系的依据. 如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
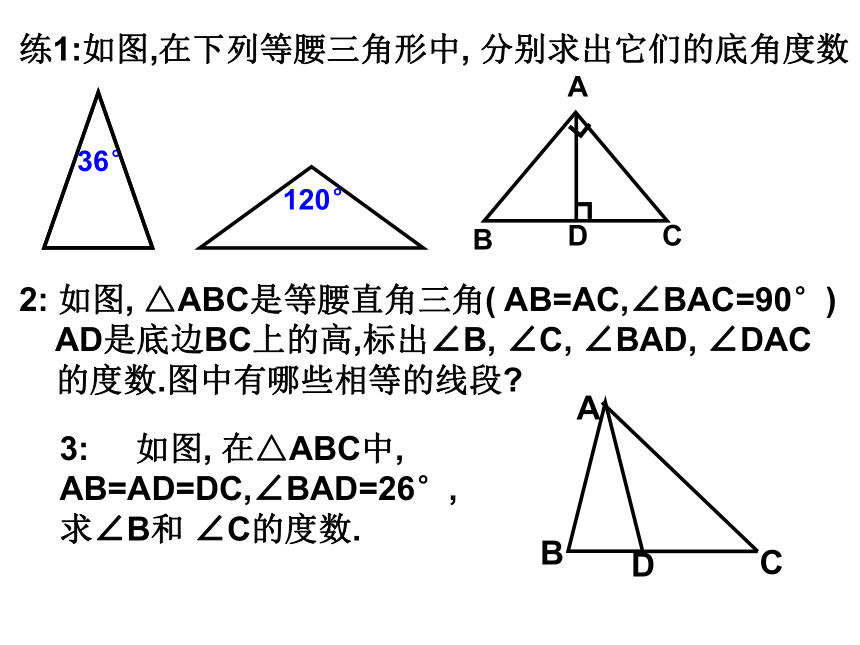
△BDC (BD=BC)36°练1:如图,在下列等腰三角形中, 分别求出它们的底角度数2: 如图, △ABC是等腰直角三角( AB=AC,∠BAC=90°)
AD是底边BC上的高,标出∠B, ∠C, ∠BAD, ∠DAC
的度数.图中有哪些相等的线段?120°3: 如图, 在△ABC中, AB=AD=DC,∠BAD=26°,
求∠B和 ∠C的度数.4. 已知等腰三角形的一个角等于36°,那么它的另外两个
角的度数分别是 ;36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9, 那么
它的周长等于 ;19 或 237. 已知等腰三角形的一个外角等于100°, 那么它的顶角
的度数是 ;80°或20°5. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;30°, 30°8. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 ;45°, 45°, 90°,或72°, 72°, 36°9. 如图,已知点D,E在BC上, AB=AC,AD=AE.
求证:BD=CE交换结论与部分已知条件,命题还成立吗?10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!ABCD(1)等腰三角形底边中点到两腰的距离相等吗?GH(2)DG,DH分别是AB、AC上的中线呢?讨论:练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。 ( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。经过本节课的学习,你有哪些收获?共同回顾
有两条边相等的三角形叫做等腰三角形。相等的两条边AB和AC叫做 腰;
另一条边BC叫做 底边;
两腰所夹的角∠BAC叫做 顶角;
底边与腰的夹角∠ABC和∠ACB叫做 底角底角底角腰腰底边顶角ABCD等腰三角形的性质: 性质1: 等腰三角形的两个底角相等
(简写成“ 等边对等角”)思考:
1.等腰三角形是轴对称图形吗?
2.对称轴有几条? 分别是什么?
3.把等腰三角形沿对称轴对折,你有哪些发现呢?已知: △ ABC中,AB=AC. 求证: ∠B= ∠C.证明:作顶角的平分线AD. 在△BAD和△CAD中,AB=AC ( 已知 ),∠ 1= ∠ 2 ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).1.已知AB=AC,则两底角∠B与∠C关系怎么样?
2.AD为∠A的角平分线,BD与CD的关系怎么样?
3.作BC的中线是否也是AD?
4.由顶点A作BC的垂线段是否也是AD?
5.刚才作的顶角平分线,底边上的中线,底边上的高这三条线是一条线段吗?为什么? 性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的
高互相重合. (通常称为“三线合一”)B例1:如图,在△ABC中, AB=AC, 点D在AC上,
且BD=BC=AD,求△ABC各角的度数.思想: 等腰三角形的性质1经常结合三角形外角性质以及三角形的内角和定理来解决有关角度计算问题.
其中等腰三 角形的性质1与三角形外角性质是建立角之间关系的依据;三角形内角和定理是建立等量关系的依据. 如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)36°练1:如图,在下列等腰三角形中, 分别求出它们的底角度数2: 如图, △ABC是等腰直角三角( AB=AC,∠BAC=90°)
AD是底边BC上的高,标出∠B, ∠C, ∠BAD, ∠DAC
的度数.图中有哪些相等的线段?120°3: 如图, 在△ABC中, AB=AD=DC,∠BAD=26°,
求∠B和 ∠C的度数.4. 已知等腰三角形的一个角等于36°,那么它的另外两个
角的度数分别是 ;36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9, 那么
它的周长等于 ;19 或 237. 已知等腰三角形的一个外角等于100°, 那么它的顶角
的度数是 ;80°或20°5. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;30°, 30°8. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 ;45°, 45°, 90°,或72°, 72°, 36°9. 如图,已知点D,E在BC上, AB=AC,AD=AE.
求证:BD=CE交换结论与部分已知条件,命题还成立吗?10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!ABCD(1)等腰三角形底边中点到两腰的距离相等吗?GH(2)DG,DH分别是AB、AC上的中线呢?讨论:练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。 ( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。经过本节课的学习,你有哪些收获?共同回顾
