乌鲁木齐 八年级 第13讲 等腰三角形的判定[上学期]
文档属性
| 名称 | 乌鲁木齐 八年级 第13讲 等腰三角形的判定[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 163.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-21 00:00:00 | ||
图片预览


文档简介
等腰三角形的判定
有信心不一定能赢,但没有信心是一定要输的,要记住,每一天都是一个阶梯,是新的一步———向着既定的目标。
知识纵横
由于等腰三角形有丰富的性质,这些性质为我们解几何题提供了新的理论依据,所以寻找发现等腰三角形是解一些几何题的关键,判定一个三角形为等腰三角形的基本方法是:从定义人手,证明一个三角形的两条边相等;从角入手,证明一个三角形的两个角相等.
实际解题中的一个常用技巧是,构造等腰三角形,进而利用等腰三角形的性质为解题服务,常用的构造方法有:
1.“角平分线+平行线”构造等腰三角形;
2.“角平分线+垂线”构造等腰三角形;
3.用“垂直平分线”构造等腰三角形;
4.用“三角形中角的2倍关系”构造等腰三角形.
【例1】如图,一个六边形的6个内角都是1200,其连续四边的长依次是1、9、
9、5(cm),那么这个六边形的周长是_______cm.
(“祖冲之杯”邀请赛试题)
思路点拨 设法将六边形的问题转化为三角形或四边形的问题加以解决,六边形的外角都为600,利用600构造等边三角形是解本例的关键.
【例21】如图,已知Rt△ABc中,∠C=900,∠A=300,在直线BC或Ac上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( ).
A.2个 B.4个 C.6个 D.8个
(第17届江苏省竞赛题)
思路点拨 AB既可作等腰△PAB的腰,也可作为等腰△PAB的底,故要思考全面,才能正确地得出符合条件的P点的个数.
【例3】 如图,△ABC中,AD⊥BC于D,∠B=2∠C,求证:AB十BD=CD.
(天津市竞赛题)
思路点拨 如何利用条件∠B=2∠C 又怎样得到AB+BD 不同的思考方向,会找到解题的不同方法.
【例4】如图甲,点C为线段AB上一点,△ACM、△CBN是等边三角形,直线AN、MC交于点E,直线BM、CN交于点F
(1)求证:AN=BM;
(2)求证:△CEF是等边三角形;
(3)将△ACM绕点C按逆时针方向旋转900,其他条件不变,在图乙中补出符合要求的图形,并判断第(1)、(2)两小题结论是否仍然成立(不要求证明).
(荆门市中考题)
… n一一
思路点拨 图甲中有多对全等三角形,这是解(1)、(2)问的基础.
【例5】 如图,在△ABC中,∠C=900,∠CAD=300,AC=BC=AD.求证:CD=BD.
(2004年重庆市竞赛题)
思路点拨 图中有300、600等特殊角,联想到相应的知识方法,就打开了解决本例的不同思路.
基础夯实
1.如图,△ABC中,BC=8cm,AB的垂直平分线交AB于D点,交AC于E点,△BCE的周长为18cm,则AC的长为_____________。
(2004年南通市中考题)
2.如图,△ABC中,AB=AC,∠B=360,D、E是BC上两点,使∠ADE=∠AED=2∠BAD,则图中等腰三角形共有_____个.
3.如图,△ABC中,AD 平分∠BAC,AB+BD=AC,则∠B:∠C的值_______。
(“五羊杯”竞赛题)
4.如图,四边形ABCD中,对角线AC与BD相交于E点,若AC平分∠DAB,且AB=AE,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③.∠DBC=∠DAB;④△ABE是等边三角形.请写出正确结论的序号_______(把你认为正确结论的序号都填上).
(天津市中考题)
5.如图,在△ABC中,∠BAC=1060,EF、MN分别是AB、AC的中垂线,E、M在BC上,则么EAM等于( ).
A .580 B.320 C.360 D.340
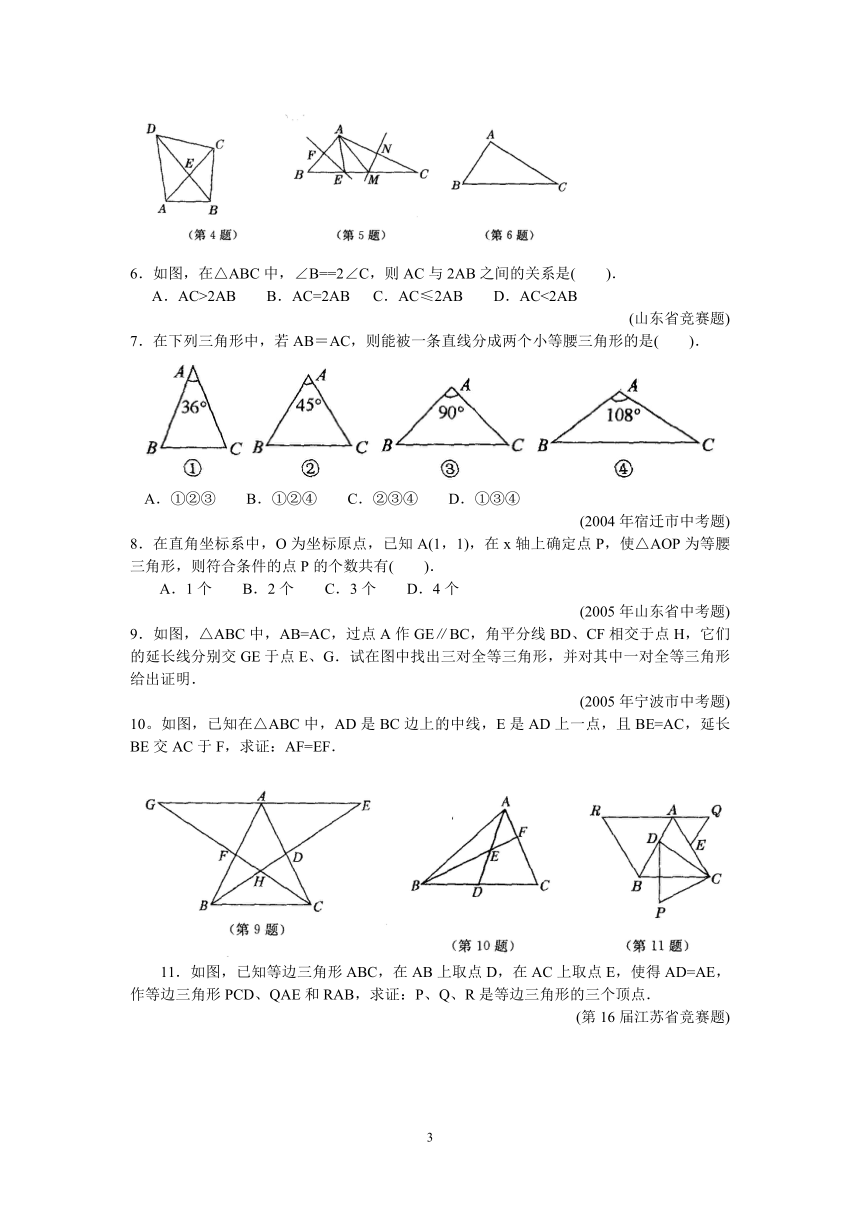
6.如图,在△ABC中,∠B==2∠C,则AC与2AB之间的关系是( ).
A.AC>2AB B.AC=2AB C.AC≤2AB D.AC<2AB
(山东省竞赛题)
7.在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( ).
A.①②③ B.①②④ C.②③④ D.①③④
(2004年宿迁市中考题)
8.在直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( ).
A.1个 B.2个 C.3个 D.4个
(2005年山东省中考题)
9.如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出三对全等三角形,并对其中一对全等三角形给出证明.
(2005年宁波市中考题)
10。如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.
11.如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD、QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
(第16届江苏省竞赛题)
能力拓展:
12.在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为am,此时梯子的倾斜角为750,如果梯子底端不动,顶端靠在对面墙上,此时梯子顶端距地面的垂直距离NB为bm,梯子的倾斜角为450,则这问房子的宽AB是_______m·
(2004年河南省中考题)
13.如图,△ABC中,AB=AC,BC=BD=ED=EA,则∠A=_____ 。
14.已知正△ABC的面积是1,P是平面上一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有_____个,△PAB的面积是_______
(第16届“希望杯”邀请赛试题)
15.有一个等腰三角形纸片,若能从一个底角的顶点出发,将其剪成两个等腰三角形纸片,则原等腰三角形纸片的顶角为_____度.
(第15届江苏省竞赛题)
16.在等边△ABC所在的平面内求一点P,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P有( ).
A.1个 B.4个 C.7个D.10个
17.如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD’的位置,则∠ADD’的度数是( ).
A.250 B.300 C.350 D.450
(2004年聊城市中考题)
18.如图,已知边长为5的等边△ABC的纸片,点E在边AC上,点F在边AB上,沿着EF折叠,使点A落在边BC上的点D位置,且ED⊥BC,则CE的长是( ).
A. B. C. D.
(2004牟镇江市中考题)
19.如图,在△ABC内,∠BAC=600,∠ACB=400,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线.求证:BQ十AQ=AB+BP.
(全国初中数学竞赛题)
20.如图,已知O是等边△ABC内的一点,∠AOB、∠BOC、∠AOC的角度之比为6:5:4,求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.
(2005年太原市竞赛题)
(第19题) (第20题)
21.如图,在△ABC中,∠BAC=900,AB=AC,D是△ABC内一点,且∠DAC=
∠DCA=150,求证:BD=BA.
22.在平面内确定四点,连接每两点,使任意三点构成等腰三角形(包括等边三角形),且每两点之问的线段长只有两个数值,则这四点的取法有多少种 画图说明. .
(潍坊市中考题)
综合创新
23.如图,在五边形ABCDE中,∠B=E,∠C=∠D,BC=DE,M为CD的中点,求证:AM⊥CD.
(武汉市选拔赛试题)
24.已知△ABC中,∠B为锐角,从顶点A向边BC或它的延长线引垂线交BC于H点,又从项点C向边AB或它的延长线引垂线交AB于K.试问:当、是整数时,△ABC是怎样的三角形 并证明你的结论.
(“智能杯”通讯赛试题)
PAGE
6
有信心不一定能赢,但没有信心是一定要输的,要记住,每一天都是一个阶梯,是新的一步———向着既定的目标。
知识纵横
由于等腰三角形有丰富的性质,这些性质为我们解几何题提供了新的理论依据,所以寻找发现等腰三角形是解一些几何题的关键,判定一个三角形为等腰三角形的基本方法是:从定义人手,证明一个三角形的两条边相等;从角入手,证明一个三角形的两个角相等.
实际解题中的一个常用技巧是,构造等腰三角形,进而利用等腰三角形的性质为解题服务,常用的构造方法有:
1.“角平分线+平行线”构造等腰三角形;
2.“角平分线+垂线”构造等腰三角形;
3.用“垂直平分线”构造等腰三角形;
4.用“三角形中角的2倍关系”构造等腰三角形.
【例1】如图,一个六边形的6个内角都是1200,其连续四边的长依次是1、9、
9、5(cm),那么这个六边形的周长是_______cm.
(“祖冲之杯”邀请赛试题)
思路点拨 设法将六边形的问题转化为三角形或四边形的问题加以解决,六边形的外角都为600,利用600构造等边三角形是解本例的关键.
【例21】如图,已知Rt△ABc中,∠C=900,∠A=300,在直线BC或Ac上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( ).
A.2个 B.4个 C.6个 D.8个
(第17届江苏省竞赛题)
思路点拨 AB既可作等腰△PAB的腰,也可作为等腰△PAB的底,故要思考全面,才能正确地得出符合条件的P点的个数.
【例3】 如图,△ABC中,AD⊥BC于D,∠B=2∠C,求证:AB十BD=CD.
(天津市竞赛题)
思路点拨 如何利用条件∠B=2∠C 又怎样得到AB+BD 不同的思考方向,会找到解题的不同方法.
【例4】如图甲,点C为线段AB上一点,△ACM、△CBN是等边三角形,直线AN、MC交于点E,直线BM、CN交于点F
(1)求证:AN=BM;
(2)求证:△CEF是等边三角形;
(3)将△ACM绕点C按逆时针方向旋转900,其他条件不变,在图乙中补出符合要求的图形,并判断第(1)、(2)两小题结论是否仍然成立(不要求证明).
(荆门市中考题)
… n一一
思路点拨 图甲中有多对全等三角形,这是解(1)、(2)问的基础.
【例5】 如图,在△ABC中,∠C=900,∠CAD=300,AC=BC=AD.求证:CD=BD.
(2004年重庆市竞赛题)
思路点拨 图中有300、600等特殊角,联想到相应的知识方法,就打开了解决本例的不同思路.
基础夯实
1.如图,△ABC中,BC=8cm,AB的垂直平分线交AB于D点,交AC于E点,△BCE的周长为18cm,则AC的长为_____________。
(2004年南通市中考题)
2.如图,△ABC中,AB=AC,∠B=360,D、E是BC上两点,使∠ADE=∠AED=2∠BAD,则图中等腰三角形共有_____个.
3.如图,△ABC中,AD 平分∠BAC,AB+BD=AC,则∠B:∠C的值_______。
(“五羊杯”竞赛题)
4.如图,四边形ABCD中,对角线AC与BD相交于E点,若AC平分∠DAB,且AB=AE,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③.∠DBC=∠DAB;④△ABE是等边三角形.请写出正确结论的序号_______(把你认为正确结论的序号都填上).
(天津市中考题)
5.如图,在△ABC中,∠BAC=1060,EF、MN分别是AB、AC的中垂线,E、M在BC上,则么EAM等于( ).
A .580 B.320 C.360 D.340
6.如图,在△ABC中,∠B==2∠C,则AC与2AB之间的关系是( ).
A.AC>2AB B.AC=2AB C.AC≤2AB D.AC<2AB
(山东省竞赛题)
7.在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( ).
A.①②③ B.①②④ C.②③④ D.①③④
(2004年宿迁市中考题)
8.在直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( ).
A.1个 B.2个 C.3个 D.4个
(2005年山东省中考题)
9.如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出三对全等三角形,并对其中一对全等三角形给出证明.
(2005年宁波市中考题)
10。如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.
11.如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD、QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
(第16届江苏省竞赛题)
能力拓展:
12.在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为am,此时梯子的倾斜角为750,如果梯子底端不动,顶端靠在对面墙上,此时梯子顶端距地面的垂直距离NB为bm,梯子的倾斜角为450,则这问房子的宽AB是_______m·
(2004年河南省中考题)
13.如图,△ABC中,AB=AC,BC=BD=ED=EA,则∠A=_____ 。
14.已知正△ABC的面积是1,P是平面上一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有_____个,△PAB的面积是_______
(第16届“希望杯”邀请赛试题)
15.有一个等腰三角形纸片,若能从一个底角的顶点出发,将其剪成两个等腰三角形纸片,则原等腰三角形纸片的顶角为_____度.
(第15届江苏省竞赛题)
16.在等边△ABC所在的平面内求一点P,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P有( ).
A.1个 B.4个 C.7个D.10个
17.如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD’的位置,则∠ADD’的度数是( ).
A.250 B.300 C.350 D.450
(2004年聊城市中考题)
18.如图,已知边长为5的等边△ABC的纸片,点E在边AC上,点F在边AB上,沿着EF折叠,使点A落在边BC上的点D位置,且ED⊥BC,则CE的长是( ).
A. B. C. D.
(2004牟镇江市中考题)
19.如图,在△ABC内,∠BAC=600,∠ACB=400,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线.求证:BQ十AQ=AB+BP.
(全国初中数学竞赛题)
20.如图,已知O是等边△ABC内的一点,∠AOB、∠BOC、∠AOC的角度之比为6:5:4,求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.
(2005年太原市竞赛题)
(第19题) (第20题)
21.如图,在△ABC中,∠BAC=900,AB=AC,D是△ABC内一点,且∠DAC=
∠DCA=150,求证:BD=BA.
22.在平面内确定四点,连接每两点,使任意三点构成等腰三角形(包括等边三角形),且每两点之问的线段长只有两个数值,则这四点的取法有多少种 画图说明. .
(潍坊市中考题)
综合创新
23.如图,在五边形ABCDE中,∠B=E,∠C=∠D,BC=DE,M为CD的中点,求证:AM⊥CD.
(武汉市选拔赛试题)
24.已知△ABC中,∠B为锐角,从顶点A向边BC或它的延长线引垂线交BC于H点,又从项点C向边AB或它的延长线引垂线交AB于K.试问:当、是整数时,△ABC是怎样的三角形 并证明你的结论.
(“智能杯”通讯赛试题)
PAGE
6
