人教版数学八年级下册17.1勾股定理 课时练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册17.1勾股定理 课时练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 617.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 08:48:50 | ||
图片预览



文档简介
17.1 勾股定理 课时练习
一、单选题
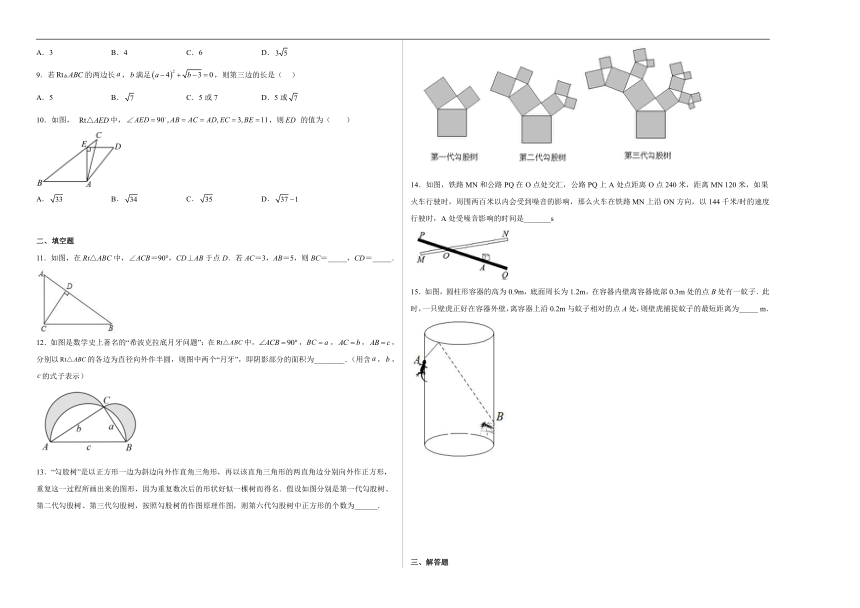
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,小正方形的面积为5,则大正方形的面积为( )
A.13 B.14 C.15 D.16
2.如图,数轴上点A对应的数是0,点B对应的数是1,,垂足为B,且,以A为圆心,为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
3.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
4.如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“勾股方圆图”(又称赵爽弦图),它是由四个全等的直角三角形(直角边分别为a,b,斜边为c)与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积为11,小正方形的面积为3,则的值为( )
A.68 B.89 C.119 D.130
5.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
6.如图,中,,将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ).
A. B. C.3 D.
7.如图,在矩形中,,点M在边上,若平分,则的长是( )
A. B. C. D.
8.在中,,,.现将按如图那样折叠,使点落在上的点处,折痕为,则的长为( )
A.3 B.4 C.6 D.
9.若的两边长,满足,则第三边的长是( )
A.5 B. C.5或7 D.5或
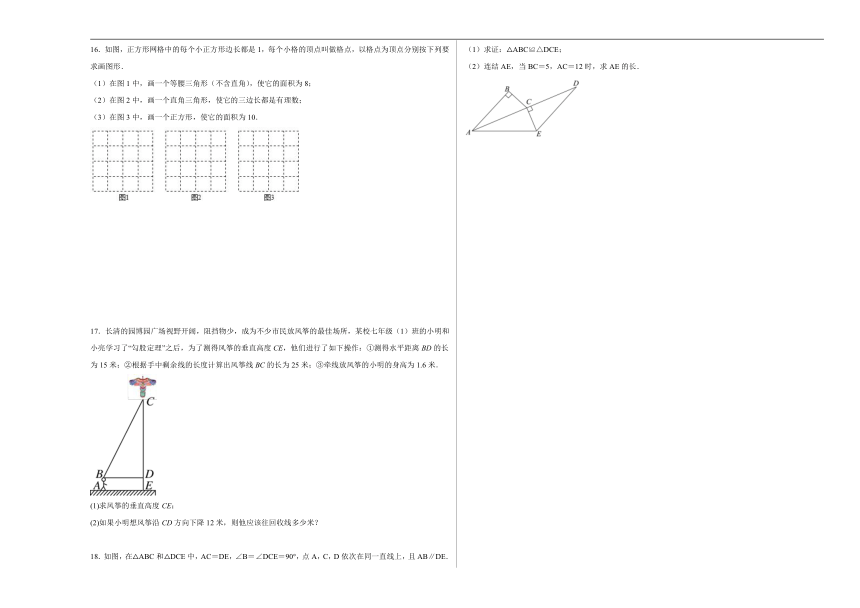
10.如图, 中,,则 的值为( )
A. B. C. D.
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC=_____,CD=_____.
12.如图是数学史上著名的“希波克拉底月牙问题”:在中,,,,,分别以的各边为直径向外作半圆,则图中两个“月牙”,即阴影部分的面积为________.(用含,,的式子表示)
13.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为______.
14.如图,铁路MN和公路PQ在O点处交汇,公路PQ上A处点距离O点240米,距离MN 120米,如果火车行驶时,周围两百米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向,以144千米/时的速度行驶时,A处受噪音影响的时间是_______s
15.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_____ m.
三、解答题
16.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
17.长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
18.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
参考答案
1.A
【详解】解:如图所示:
∵(a+b)2=21,
∴a2+2ab+b2=21①,
∵小正方形的面积为5,
∴(a-b)2= a2-2ab+b2=5②,
①+②得:2a2+2b2=26,
∴大正方形的面积为a2+b2=13,
故选:A.
.
2.D
【详解】解:∵,
∴=,
∴,
∵以为圆心,为半径画弧,交数轴于点,
∴,
∴点表示的数是:.
故选D.
3.A
【详解】解:如图:
由题意可知:,米,
设米,则米,
由勾股定理可得:,即,
解得:米,米(舍去).
故选:A
4.B
【详解】解:大正方形的面积为:,
小正方形的面积为:,
由得,
,即,
,
故选B.
5.B
【详解】图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
6.D
【详解】解:∵D是AB中点,AB=4,
∴AD=BD=2,
∵将△ABC折叠,使点C与AB的中点D重合,
∴DN=CN,
∴BN=BC-CN=6-DN,
在Rt△DBN中,DN2=BN2+DB2,
∴DN2=(6-DN)2+4,
∴DN=,
∴CN=DN=,
故选:D.
7.D
【详解】解:过点A作AE⊥DM于E,如图,
∵矩形,
∴∠B=∠C=90°,CD=AB=1,BC=AD=2,
∵AE⊥DM于E,
∠AEM=∠AED=90°,
∴∠B=∠AEM,
∵平分,
∴∠AMB=∠AME,
∵AM=AM,
∴△ABM≌△AEM(AAS),
∴AE=AB=1,BM=ME,
在Rt△AED中,由勾股定理,得DE=,
设BM=ME=x,则CM=2-x,DE=+x,
在Rt△CDM中,由勾股定理,得
(+x)2=(2-x)2+12,
解得:x=2-,
∴CM=2-(2-)=,
故选:D.
8.A
【详解】解:在中,由勾股定理得,,
∵将沿折叠,点与点重合,
∴,,
∴
设,
则,,
在中,由勾股定理得,,即
解得,
∴,
故选:A.
9.D
【详解】解:∵
又∵,
∴
∴
设第三边长为x,由则共有以下两种情况:
①当时,
②当时,由所以,
∴第三边长是5或;
故选:D.
10.A
【详解】解:如图:过A作垂足为F
∵
∴
∵,
∴
∴
在中,由勾股定理得,,
在中,由勾股定理得,
又∵,
∴
在中,由勾股定理得:
∴
∴ .
故选:A.
11. 4
【详解】解:∵∠ACB=90°,AC=3,AB=5,
∴BC=,
∵CD⊥AB,
∴S△ABC=AB×CD=AC×BC,
∴CD= ,
故答案为:4,.
12.
【详解】解:根据题意得:阴影部分的面积等于两个小半圆的面积之和加上直角三角形ABC的面积减去大半圆的面积,
∵在中,,,,,
∴,
∴阴影部分的面积等于
.
故答案为:
13.127
【详解】解:∵第一代勾股树中正方形有1+2=3(个),
第二代勾股树中正方形有1+2+22=7(个),
第三代勾股树中正方形有1+2+22+23=15(个),
......
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),
故答案为:127.
14.8
【详解】解:如图:过点A作AC⊥ON,AB=AD=200米,
∵公路PQ上A处点距离O点240米,距离MN 120米,
∴AC=120米,
当火车到B点时对A处产生噪音影响,此时AB=200米,
∵AB=200米,AC=120米,
∴由勾股定理得:BC=160米,CD=160米,即BD=320米,
∵144千米/小时=40米/秒,
∴影响时间应是:320÷40=8秒.
故答案为:8.
15.1
【详解】解:如图,将容器侧面展开,作点A关于EF的对称点A′,连接A′B,
则A′B为最短距离.
由题意知,A′D=0.6m,A′E=AE=0.2m,
∴BD=0.9-0.3+0.2=0.8m,
∴A′B=
=
=1(m).
故答案为:1.
16.(1)作图见详解;(2)作图见详解;(3)作图见详解.
【详解】(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
17.(1)风筝的高度CE为21.6米;
(2)他应该往回收线8米.
【详解】(1)解:在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=252-152=400,
所以,CD=20(负值舍去),
所以,CE=CD+DE=20+1.6=21.6(米),
答:风筝的高度CE为21.6米;
(2)解:由题意得,CM=12米,
∴DM=8米,
∴BM= (米),
∴BC-BM=25-17=8(米),
∴他应该往回收线8米.
18.(1)见解析;(2)13
【详解】解:(1)∵
∴
在△ABC和△DCE中
∴△ABC≌△DCE
(2)由(1)可得BC=CE=5
在直角三角形ACE中
一、单选题
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,小正方形的面积为5,则大正方形的面积为( )
A.13 B.14 C.15 D.16
2.如图,数轴上点A对应的数是0,点B对应的数是1,,垂足为B,且,以A为圆心,为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
3.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
4.如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“勾股方圆图”(又称赵爽弦图),它是由四个全等的直角三角形(直角边分别为a,b,斜边为c)与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积为11,小正方形的面积为3,则的值为( )
A.68 B.89 C.119 D.130
5.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
6.如图,中,,将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ).
A. B. C.3 D.
7.如图,在矩形中,,点M在边上,若平分,则的长是( )
A. B. C. D.
8.在中,,,.现将按如图那样折叠,使点落在上的点处,折痕为,则的长为( )
A.3 B.4 C.6 D.
9.若的两边长,满足,则第三边的长是( )
A.5 B. C.5或7 D.5或
10.如图, 中,,则 的值为( )
A. B. C. D.
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC=_____,CD=_____.
12.如图是数学史上著名的“希波克拉底月牙问题”:在中,,,,,分别以的各边为直径向外作半圆,则图中两个“月牙”,即阴影部分的面积为________.(用含,,的式子表示)
13.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为______.
14.如图,铁路MN和公路PQ在O点处交汇,公路PQ上A处点距离O点240米,距离MN 120米,如果火车行驶时,周围两百米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向,以144千米/时的速度行驶时,A处受噪音影响的时间是_______s
15.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_____ m.
三、解答题
16.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
17.长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
18.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
参考答案
1.A
【详解】解:如图所示:
∵(a+b)2=21,
∴a2+2ab+b2=21①,
∵小正方形的面积为5,
∴(a-b)2= a2-2ab+b2=5②,
①+②得:2a2+2b2=26,
∴大正方形的面积为a2+b2=13,
故选:A.
.
2.D
【详解】解:∵,
∴=,
∴,
∵以为圆心,为半径画弧,交数轴于点,
∴,
∴点表示的数是:.
故选D.
3.A
【详解】解:如图:
由题意可知:,米,
设米,则米,
由勾股定理可得:,即,
解得:米,米(舍去).
故选:A
4.B
【详解】解:大正方形的面积为:,
小正方形的面积为:,
由得,
,即,
,
故选B.
5.B
【详解】图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
6.D
【详解】解:∵D是AB中点,AB=4,
∴AD=BD=2,
∵将△ABC折叠,使点C与AB的中点D重合,
∴DN=CN,
∴BN=BC-CN=6-DN,
在Rt△DBN中,DN2=BN2+DB2,
∴DN2=(6-DN)2+4,
∴DN=,
∴CN=DN=,
故选:D.
7.D
【详解】解:过点A作AE⊥DM于E,如图,
∵矩形,
∴∠B=∠C=90°,CD=AB=1,BC=AD=2,
∵AE⊥DM于E,
∠AEM=∠AED=90°,
∴∠B=∠AEM,
∵平分,
∴∠AMB=∠AME,
∵AM=AM,
∴△ABM≌△AEM(AAS),
∴AE=AB=1,BM=ME,
在Rt△AED中,由勾股定理,得DE=,
设BM=ME=x,则CM=2-x,DE=+x,
在Rt△CDM中,由勾股定理,得
(+x)2=(2-x)2+12,
解得:x=2-,
∴CM=2-(2-)=,
故选:D.
8.A
【详解】解:在中,由勾股定理得,,
∵将沿折叠,点与点重合,
∴,,
∴
设,
则,,
在中,由勾股定理得,,即
解得,
∴,
故选:A.
9.D
【详解】解:∵
又∵,
∴
∴
设第三边长为x,由则共有以下两种情况:
①当时,
②当时,由所以,
∴第三边长是5或;
故选:D.
10.A
【详解】解:如图:过A作垂足为F
∵
∴
∵,
∴
∴
在中,由勾股定理得,,
在中,由勾股定理得,
又∵,
∴
在中,由勾股定理得:
∴
∴ .
故选:A.
11. 4
【详解】解:∵∠ACB=90°,AC=3,AB=5,
∴BC=,
∵CD⊥AB,
∴S△ABC=AB×CD=AC×BC,
∴CD= ,
故答案为:4,.
12.
【详解】解:根据题意得:阴影部分的面积等于两个小半圆的面积之和加上直角三角形ABC的面积减去大半圆的面积,
∵在中,,,,,
∴,
∴阴影部分的面积等于
.
故答案为:
13.127
【详解】解:∵第一代勾股树中正方形有1+2=3(个),
第二代勾股树中正方形有1+2+22=7(个),
第三代勾股树中正方形有1+2+22+23=15(个),
......
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),
故答案为:127.
14.8
【详解】解:如图:过点A作AC⊥ON,AB=AD=200米,
∵公路PQ上A处点距离O点240米,距离MN 120米,
∴AC=120米,
当火车到B点时对A处产生噪音影响,此时AB=200米,
∵AB=200米,AC=120米,
∴由勾股定理得:BC=160米,CD=160米,即BD=320米,
∵144千米/小时=40米/秒,
∴影响时间应是:320÷40=8秒.
故答案为:8.
15.1
【详解】解:如图,将容器侧面展开,作点A关于EF的对称点A′,连接A′B,
则A′B为最短距离.
由题意知,A′D=0.6m,A′E=AE=0.2m,
∴BD=0.9-0.3+0.2=0.8m,
∴A′B=
=
=1(m).
故答案为:1.
16.(1)作图见详解;(2)作图见详解;(3)作图见详解.
【详解】(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
17.(1)风筝的高度CE为21.6米;
(2)他应该往回收线8米.
【详解】(1)解:在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=252-152=400,
所以,CD=20(负值舍去),
所以,CE=CD+DE=20+1.6=21.6(米),
答:风筝的高度CE为21.6米;
(2)解:由题意得,CM=12米,
∴DM=8米,
∴BM= (米),
∴BC-BM=25-17=8(米),
∴他应该往回收线8米.
18.(1)见解析;(2)13
【详解】解:(1)∵
∴
在△ABC和△DCE中
∴△ABC≌△DCE
(2)由(1)可得BC=CE=5
在直角三角形ACE中
