18.2.2平行四边形的判定(2) 课件(共24张PPT)
文档属性
| 名称 | 18.2.2平行四边形的判定(2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
18.2.2平行四边形的判定(2)
华师大版 八年级 下册
教学目标
教学目标:1.掌握用“对角线互相平分的四边形是平行四边形”这一判
定定理.
2.利用平行四边形的判定进行简单的推理和证明.
教学重点:理解并掌握平行四边形的判定定理3.
教学难点:平行四边形的判定定理与性质的综合运用.
新知导入
情境引入
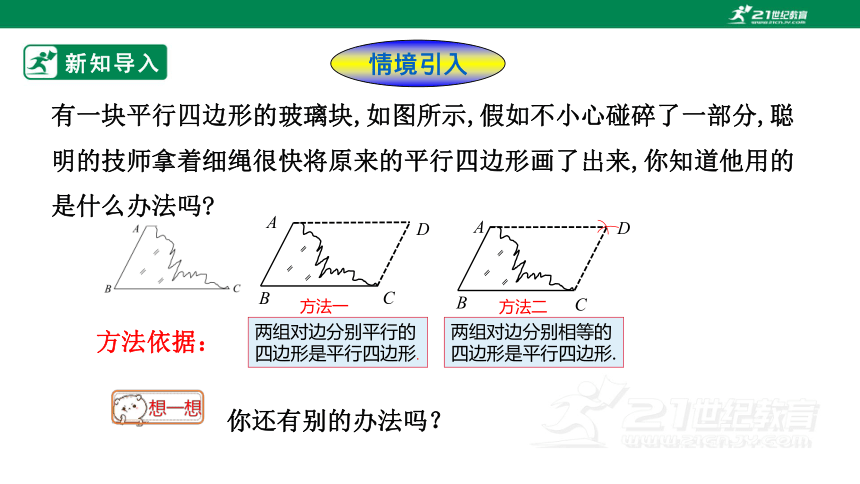
有一块平行四边形的玻璃块,如图所示,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么办法吗
D
A
B
C
两组对边分别平行的四边形是平行四边形.
D
A
B
C
两组对边分别相等的四边形是平行四边形.
方法依据:
你还有别的办法吗?
方法一
方法二
新知讲解
合作学习
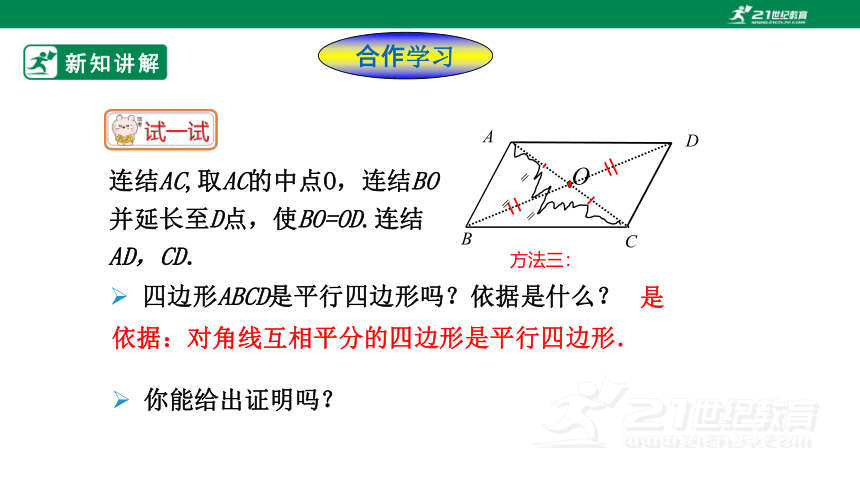
连结AC,取AC的中点O,连结BO并延长至D点,使BO=OD.连结AD,CD.
你能给出证明吗?
D
O
A
B
C
依据:对角线互相平分的四边形是平行四边形.
方法三:
四边形ABCD是平行四边形吗?依据是什么?
是
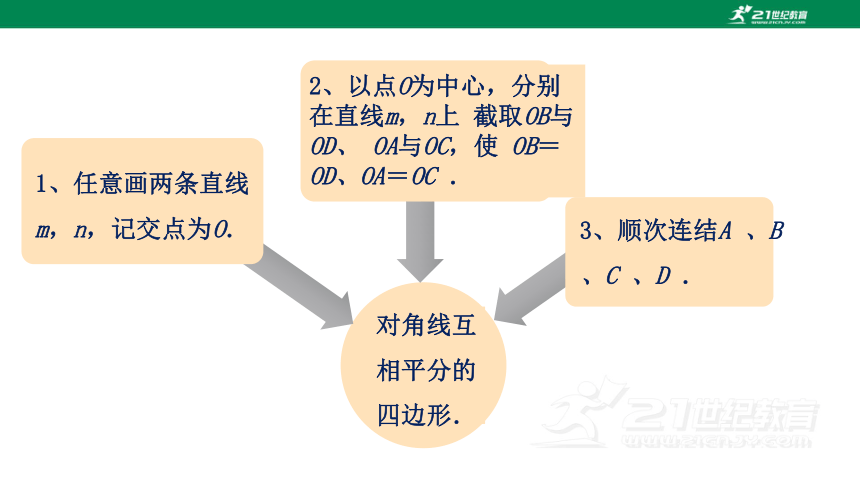
对角线互相平分的四边形.
1、任意画两条直线m,n,记交点为O.
2、以点O为中心,分别在直线m,n上 截取OB与OD、 OA与OC,使 OB=OD、OA=OC .
3、顺次连结A 、B、C 、D .
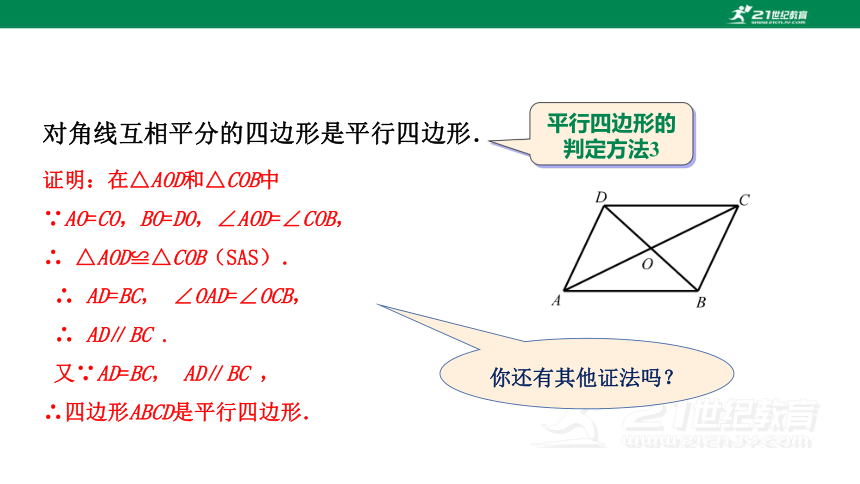
对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
证明:在△AOD和△COB中
∵AO=CO,BO=DO,∠AOD=∠COB,
∴ △AOD≌△COB(SAS).
∴ AD=BC, ∠OAD=∠OCB,
∴ AD∥BC .
又∵AD=BC, AD∥BC ,
∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法3
你还有其他证法吗?
提炼概念
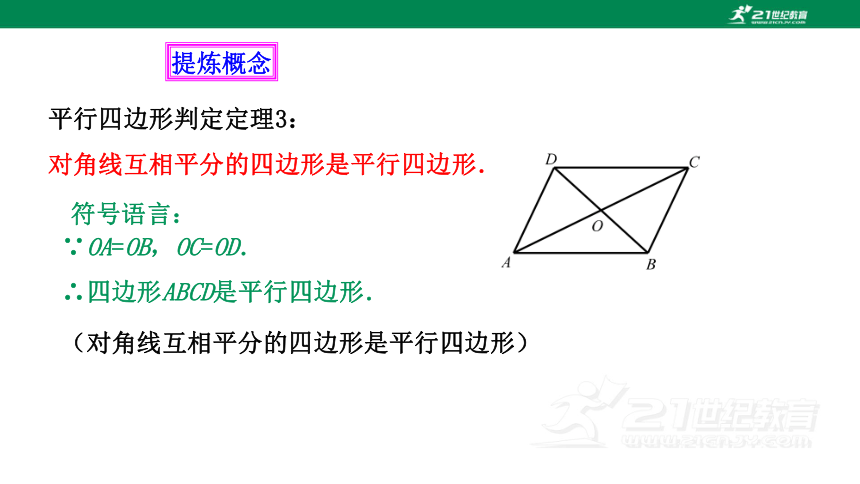
平行四边形判定定理3:
对角线互相平分的四边形是平行四边形.
符号语言:
∵OA=OB,OC=OD.
∴四边形ABCD是平行四边形.
(对角线互相平分的四边形是平行四边形)
典例精讲
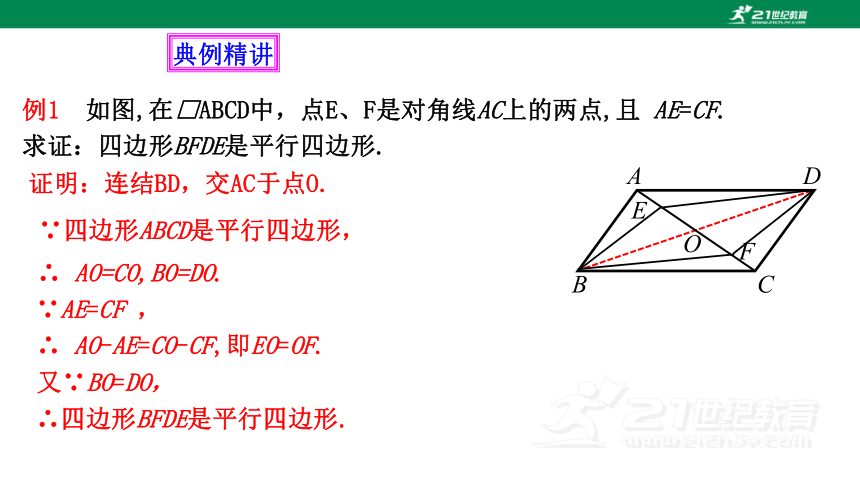
例1 如图,在□ABCD中,点E、F是对角线AC上的两点,且 AE=CF.
求证:四边形BFDE是平行四边形.
证明:连结BD,交AC于点O.
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
B
O
D
A
C
E
F
∵四边形ABCD是平行四边形,
例2 已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
证明:∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
例3:如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
证明:∵四边形AEFD是平行四边形,
∴AD=EF,且AD∥EF,
同理可得BC=EF,且BC∥EF,
∴AD=BC,且AD∥BC,
∴四边形ABCD为平行四边形.
例4 如图,G、H是□ABCD对角线AC上的两点,且AC=CH,E、F分别是AB和CD的中点.
求证:四边形EHFG是平行四边形.
证明:连接EF交AC于点O .
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD .
又∵E,F是AB,CD的中点,
∴AE=CF,
又∵ AB∥CD,∠EAO=∠FCO,
在△EAO与△COF中,
∵∠EAO=∠FCO,∠AOE=∠COF,AE=CF.
∴ △AOE≌△COF.
∴OE=OF,OA=OC.
又∵AG=CH,
∴OG=OH,
∴四边形EFHG是平行四边形.
归纳概念
平行四边形的判定方法
边
对角线
1.两组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
(判定定理1)
3.一组对边平行且相等相等的四边形是平行四边形
(判定定理2)
4.对角线互相平分的四边形是平行四边形
(判定定理3)
课堂练习
1.根据下列条件,不能判定四边形为平行四边形的是( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行
C
2.判断对错:
(1)对角线互相平分的四边形是平行四边形. ( )
(2)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(3)有一组对角相等且一组对边平行的四边形是平行
四边形. ( )
√
×
√
3.如图,线段AB,CD相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成______个平行四边形.
4
4.如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线.证明:四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线,
∴∠B=∠D,AB=CD,∠BAE= ∠DAB , ∠DCF= ∠BCD),
∴ ∠BAE= ∠DCF, △ABE≌ △CDF(ASA) .
∴BE=DF,∴AF=CE.
∵AF∥CE,
∴四边形AFCE是平行四边形.
5. 如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.
O
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂总结
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形. ∵AB∥CD,AD∥BC,
∴是平行四边形.
定理1 两组对边分别相等的四边形是平等四边形. ∵AB=CD,AD= BC,
∴是平行四边形.
定理2 一组对边平行且相等的四边形是平等四边形. ∵AB∥CD,AB=CD,
∴是平行四边形.
定理3 对角线互相平分的四边形是平行四边形. ∵OA=OC,OB=OD,
∴是平行四边形.
推论 两组对角分别相等的四边形是平行四边形. ∵∠A=∠C,∠B=∠D,
∴是平行四边形.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.2.2平行四边形的判定(2)
华师大版 八年级 下册
教学目标
教学目标:1.掌握用“对角线互相平分的四边形是平行四边形”这一判
定定理.
2.利用平行四边形的判定进行简单的推理和证明.
教学重点:理解并掌握平行四边形的判定定理3.
教学难点:平行四边形的判定定理与性质的综合运用.
新知导入
情境引入
有一块平行四边形的玻璃块,如图所示,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么办法吗
D
A
B
C
两组对边分别平行的四边形是平行四边形.
D
A
B
C
两组对边分别相等的四边形是平行四边形.
方法依据:
你还有别的办法吗?
方法一
方法二
新知讲解
合作学习
连结AC,取AC的中点O,连结BO并延长至D点,使BO=OD.连结AD,CD.
你能给出证明吗?
D
O
A
B
C
依据:对角线互相平分的四边形是平行四边形.
方法三:
四边形ABCD是平行四边形吗?依据是什么?
是
对角线互相平分的四边形.
1、任意画两条直线m,n,记交点为O.
2、以点O为中心,分别在直线m,n上 截取OB与OD、 OA与OC,使 OB=OD、OA=OC .
3、顺次连结A 、B、C 、D .
对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
证明:在△AOD和△COB中
∵AO=CO,BO=DO,∠AOD=∠COB,
∴ △AOD≌△COB(SAS).
∴ AD=BC, ∠OAD=∠OCB,
∴ AD∥BC .
又∵AD=BC, AD∥BC ,
∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法3
你还有其他证法吗?
提炼概念
平行四边形判定定理3:
对角线互相平分的四边形是平行四边形.
符号语言:
∵OA=OB,OC=OD.
∴四边形ABCD是平行四边形.
(对角线互相平分的四边形是平行四边形)
典例精讲
例1 如图,在□ABCD中,点E、F是对角线AC上的两点,且 AE=CF.
求证:四边形BFDE是平行四边形.
证明:连结BD,交AC于点O.
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
B
O
D
A
C
E
F
∵四边形ABCD是平行四边形,
例2 已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
证明:∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
例3:如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
证明:∵四边形AEFD是平行四边形,
∴AD=EF,且AD∥EF,
同理可得BC=EF,且BC∥EF,
∴AD=BC,且AD∥BC,
∴四边形ABCD为平行四边形.
例4 如图,G、H是□ABCD对角线AC上的两点,且AC=CH,E、F分别是AB和CD的中点.
求证:四边形EHFG是平行四边形.
证明:连接EF交AC于点O .
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD .
又∵E,F是AB,CD的中点,
∴AE=CF,
又∵ AB∥CD,∠EAO=∠FCO,
在△EAO与△COF中,
∵∠EAO=∠FCO,∠AOE=∠COF,AE=CF.
∴ △AOE≌△COF.
∴OE=OF,OA=OC.
又∵AG=CH,
∴OG=OH,
∴四边形EFHG是平行四边形.
归纳概念
平行四边形的判定方法
边
对角线
1.两组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
(判定定理1)
3.一组对边平行且相等相等的四边形是平行四边形
(判定定理2)
4.对角线互相平分的四边形是平行四边形
(判定定理3)
课堂练习
1.根据下列条件,不能判定四边形为平行四边形的是( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行
C
2.判断对错:
(1)对角线互相平分的四边形是平行四边形. ( )
(2)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(3)有一组对角相等且一组对边平行的四边形是平行
四边形. ( )
√
×
√
3.如图,线段AB,CD相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成______个平行四边形.
4
4.如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线.证明:四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线,
∴∠B=∠D,AB=CD,∠BAE= ∠DAB , ∠DCF= ∠BCD),
∴ ∠BAE= ∠DCF, △ABE≌ △CDF(ASA) .
∴BE=DF,∴AF=CE.
∵AF∥CE,
∴四边形AFCE是平行四边形.
5. 如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.
O
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂总结
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形. ∵AB∥CD,AD∥BC,
∴是平行四边形.
定理1 两组对边分别相等的四边形是平等四边形. ∵AB=CD,AD= BC,
∴是平行四边形.
定理2 一组对边平行且相等的四边形是平等四边形. ∵AB∥CD,AB=CD,
∴是平行四边形.
定理3 对角线互相平分的四边形是平行四边形. ∵OA=OC,OB=OD,
∴是平行四边形.
推论 两组对角分别相等的四边形是平行四边形. ∵∠A=∠C,∠B=∠D,
∴是平行四边形.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
