18.1勾股定理1
图片预览




文档简介
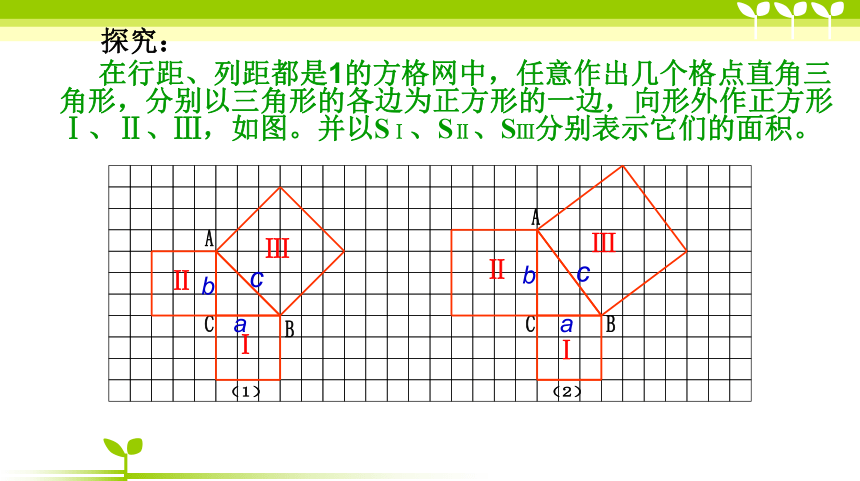
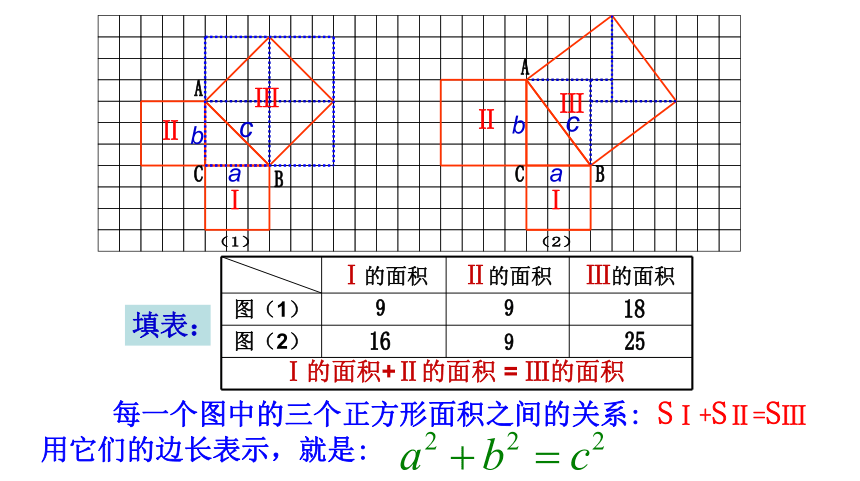
课件15张PPT。18.1 勾股定理(1)ABCABC(1)(2)bacabc 在行距、列距都是1的方格网中,任意作出几个格点直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形Ⅰ、Ⅱ、Ⅲ,如图。并以SⅠ、SⅡ、SⅢ分别表示它们的面积。探究:ⅡⅠⅢⅡⅠⅢ(1)(2)填表:Ⅰ的面积+Ⅱ的面积 = Ⅲ的面积 每一个图中的三个正方形面积之间的关系: SⅠ+SⅡ=SⅢ用它们的边长表示,就是:bacabc直角三角形两直角边长的平方和等于斜边的平方。如果直角三角形两直角边分别为a、b,斜边为c,那么(2)使用前提是直角三角形(3)分清直角边、斜边勾股定理 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三国时期我国数学家赵爽就用弦图证明了勾股定理。2002年,世界数学家大会在北京召开,大会会徽上的图形就是我国古代数学家赵爽为证明勾股定理所做的“弦图”。用它作为会徽是国际数学界对我国古代数学伟大成就的肯定。
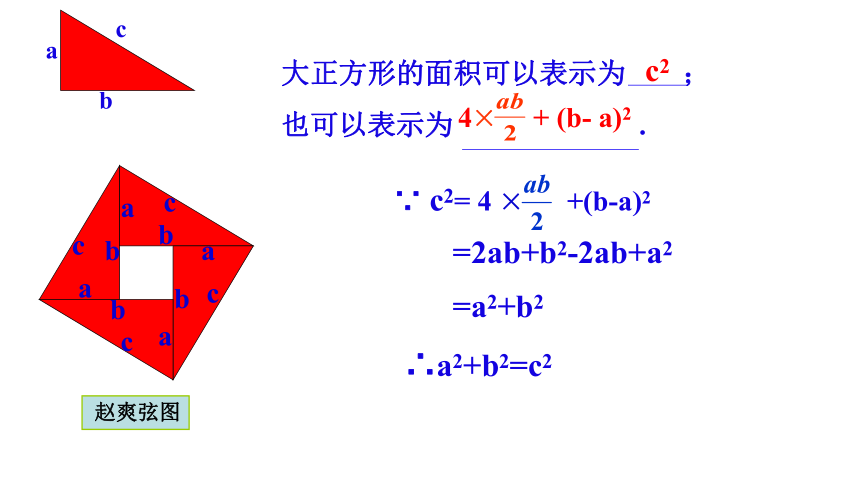
赵爽弦图2002年世界数学家大会会徽利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设直角三角形的两 条直角 边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看。3、你拼的正方形中是否含有以斜边c为边的正方形?4、你能否就你拼出的图说明a2+b2=c2?=2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为 .c2 赵爽弦图a2+2ab+b2 = c2 +2ab∴ a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为 .(a+b)2美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 ,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 1.下列说法正确的是( ) B.若a,b,c是直角三角形的三边长,则C.若a,b,c是直角三角形的三边长,且∠C=90°,则D.以上都不对CA.若a,b,c是三角形的三边长,则2.在Rt△ABC中,∠C =90°,AB =c,BC =a,AC =b.
(1)A = 6,b = 8,求c; (2)a = 8,c =17,求b.3.在Rt△ABC中,∠B=90°,a =3,b =4,求c.4.在直角三角形中,已知两边的长为3和4,则第三边长
为 . 5.长方形ABCD如图折叠,使点D落在BC边上的点F处,
已知AB=8,BC=10,(1)求DE的长,(2)求折痕AE的长。ABCDFE810810106xx8-x4?谢谢同学们的合作
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三国时期我国数学家赵爽就用弦图证明了勾股定理。2002年,世界数学家大会在北京召开,大会会徽上的图形就是我国古代数学家赵爽为证明勾股定理所做的“弦图”。用它作为会徽是国际数学界对我国古代数学伟大成就的肯定。
赵爽弦图2002年世界数学家大会会徽利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设直角三角形的两 条直角 边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看。3、你拼的正方形中是否含有以斜边c为边的正方形?4、你能否就你拼出的图说明a2+b2=c2?=2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为 .c2 赵爽弦图a2+2ab+b2 = c2 +2ab∴ a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为 .(a+b)2美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 ,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 1.下列说法正确的是( ) B.若a,b,c是直角三角形的三边长,则C.若a,b,c是直角三角形的三边长,且∠C=90°,则D.以上都不对CA.若a,b,c是三角形的三边长,则2.在Rt△ABC中,∠C =90°,AB =c,BC =a,AC =b.
(1)A = 6,b = 8,求c; (2)a = 8,c =17,求b.3.在Rt△ABC中,∠B=90°,a =3,b =4,求c.4.在直角三角形中,已知两边的长为3和4,则第三边长
为 . 5.长方形ABCD如图折叠,使点D落在BC边上的点F处,
已知AB=8,BC=10,(1)求DE的长,(2)求折痕AE的长。ABCDFE810810106xx8-x4?谢谢同学们的合作
