六年级下册数学课件-第4讲《圆柱的认识与计算》 人教版(共35张PPT)
文档属性
| 名称 | 六年级下册数学课件-第4讲《圆柱的认识与计算》 人教版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
圆柱的认识
与计算
情境导入
嗨,我今天买了张海报,东77的~哈哈哈,打开给你瞧瞧
谁啊,不认识,没听过,又不是C罗,不看不看~
新知探究
我知道,就像我的保温杯一样~可以泡枸杞
超市旋转门貌似是这样子的,旋转门,当然是旋转啦~
同学们,今天我们认识下圆柱,大家说说它有什么特点
都说面动成体,怎么可以得到圆柱呢?
Good
新知探究
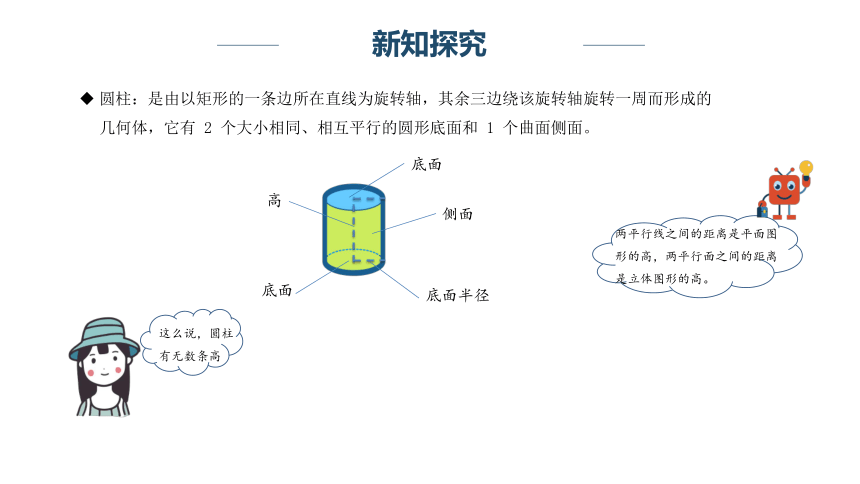
圆柱:是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体,它有 2 个大小相同、相互平行的圆形底面和 1 个曲面侧面。
两平行线之间的距离是平面图形的高,两平行面之间的距离是立体图形的高。
底面
底面
侧面
高
底面半径
这么说,圆柱有无数条高
数学例题
例题1:请在下图中标出相应位置的名称。
答案:
( )
( )
( )
( )
巩固练习
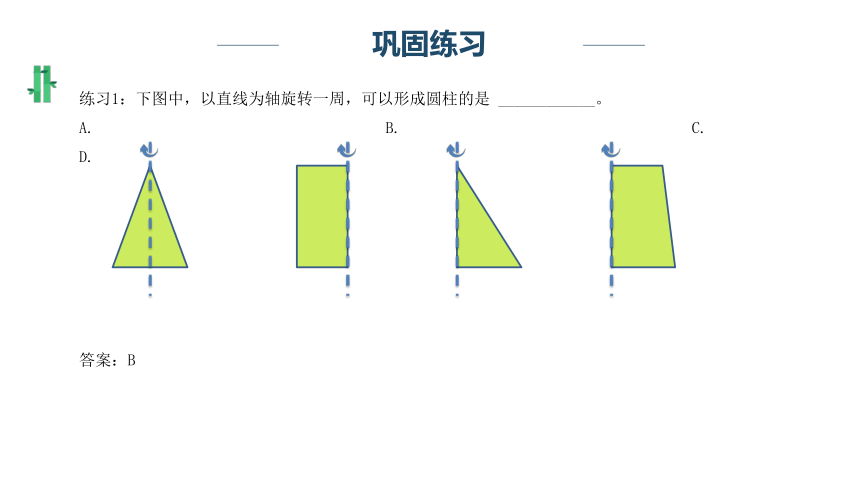
练习1:下图中,以直线为轴旋转一周,可以形成圆柱的是 ____________。
A. B. C. D.
答案:B
新知探究
我知道,两个圆,再加上侧面,可侧面咋算啊!
表面积,就是把圆柱的三个面的面积加起来
同学们,下面我们来研究下圆柱的表面积
有思路了吧?
新知探究
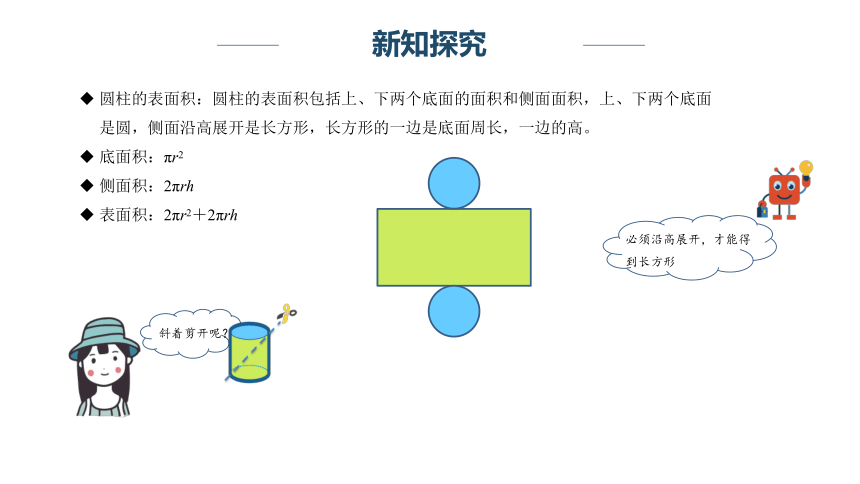
圆柱的表面积:圆柱的表面积包括上、下两个底面的面积和侧面面积,上、下两个底面是圆,侧面沿高展开是长方形,长方形的一边是底面周长,一边的高。
底面积:πr2
侧面积:2πrh
表面积:2πr2+2πrh
必须沿高展开,才能得到长方形
斜着剪开呢?
数学例题
例题2:
(1)一个圆柱的侧面展开后得到一个长方形,长是 12.56cm,宽是 3cm,这个圆柱的侧面积是 ____________cm2。
(2)一个圆柱的侧面展开后得到一个正方形,边长是 9.42cm,这个圆柱的底面周长是 ____________cm,高是 ____________cm。
答案:
(1)37.68
(2)9.42;9.42
巩固练习
练习2:一张长方形纸,长为 25cm,宽为 14cm.把这张长方形纸卷成一个圆柱体,这个圆柱体的底面周长是多少厘米?圆柱体的高是多少厘米?(接头处长度忽略不计)
答案:底面周长是25厘米,高14厘米或底面周长是14厘米,高25厘米
数学例题
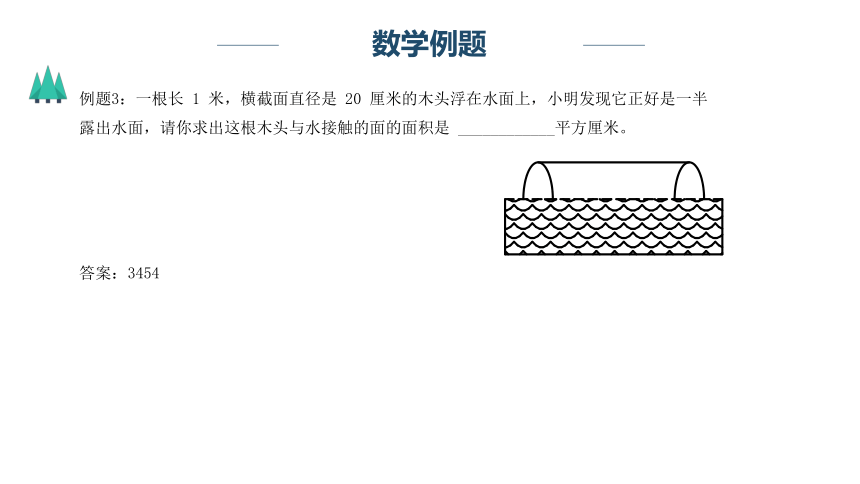
例题3:一根长 1 米,横截面直径是 20 厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 ____________平方厘米。
答案:3454
巩固练习
练习3:一个圆柱分成相等的四个圆柱,表面积增加 18.84 平方分米,则圆柱的一个底面的面积是多少平方分米?
答案:6.28平方分米
数学例题
例题4:妙妙过生日的时候,妈妈给她买了一个豪华大蛋糕,总共有3层,每层都是圆柱形,每层高1分米,从上往下的半径分别是10厘米,20厘米,30厘米,求这个蛋糕的表面积是多少平方厘米?(包括最下层底面的面积)
答案:9420平方厘米
巩固练习
练习4:有一个圆柱体的零件,高 10 厘米,底面直径是 6 厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是 4 厘米,孔深 5 厘米(如图), 如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米 (π 取 3.14)
答案:307.72平方厘米
新知探究
我知道,圆柱的体积就是圆柱所占空间的大小!
体积都这样,问题是怎么算呢?
同学们,学习了表面积,下面该学习圆柱体积了
是不是很熟悉!
新知探究
圆柱的体积:类似于圆面积公式的推导方法,把圆柱分割成若干小份,拼成一个近似的长方体,圆柱的体积等于近似的长方体的体积。
长方体长→圆柱底面周长的一半(πr)
长方体宽→圆柱底面半径(r)
长方体高→圆柱高(h)
圆柱体积:πr×r×h=πr2h
πr2是圆柱底面积,那么圆柱体积也可以用“底面积×高”表示!
三棱柱、四棱柱、五棱柱、六棱柱、圆柱……体积都是这样算的!
数学例题
例题5:求下面圆柱的表面积和体积。(π 取 3.14)
答案:
图1:150.72平方厘米,141.3立方厘米
图2:113.04平方分米,87.92立方分米
3厘米
5厘米
7分米
2分米
巩固练习
练习5:一个圆柱形无盖的水桶,底面的直径是 6dm,高是 4dm,做这样一个水桶,需要多少平方分米的铁皮?它的容积是多少?(π 取 3.14)
答案:103.62平方厘米;113.04升
数学例题
例题6:一张长方形纸片,长 10 厘米,宽 4 厘米,以这个长方形的长或宽为轴,将这个长方形旋转 360度,可以得到两个不同的圆柱体,求这两个圆柱的表面积之比、体积之比的侧面积之比分别是多少?
答案:
表面积之比,5:2
体积之比,5:2
侧面积之比,1:1
巩固练习
练习6:现有长是 5 厘米,宽是 3 厘米的长方形,以下面的四种方式进行旋转,可以得到四个不同的圆柱,试判断哪种方式得到的圆柱体积最大。
答案:图3得到的体积最大
数学例题
例题7:一个圆柱的高增加 3 分米 , 表面积就增加 56.52 平方分米 , 它的体积增加多少立方分米
答案:84.78立方分米
巩固练习
练习7:一个圆柱被截去 5cm 后,圆柱的表面积减少了 62.8cm2,原来圆柱的表面积是多少平方厘米?
答案:276.32平方厘米
数学例题
例题8:一个圆柱体形状的木棒 , 沿着底面直径竖直切成两部分 ,已知这两部分的表面积之和比圆柱体的表面积大 2008cm2,则这个圆柱体木棒的侧面积是 ____________cm2 。(π 取 3.14)
答案:3152.56
巩固练习
练习8:如图,由底面半径是3分米的圆柱切割而成的不规则几何体,求这个几何体的体积?(π 取 3.14)
答案:197.82立方分米
8分米
6分米
数学例题
例题9:如图,一个瓶子的瓶身呈圆柱形(不计瓶颈),已知瓶内装有 1.6 升的水,当瓶子正放时瓶内水面高 12 厘米,当瓶子倒放时瓶内空余部分高 3 厘米,问瓶子的容积是多少升?
答案:2升
巩固练习
练习9:一个酒瓶里面深 30 厘米,底面内直径是 10 厘米,瓶里酒深 15 厘米,把酒瓶塞紧后使其瓶口向下倒立,这时酒深 25 厘米,酒瓶的容积是多少立方厘米?
答案:1570立方厘米
数学例题
例题10:如图,底面积为 50 平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为 5 厘米的正方体木块,木块浮出水面的高度是 3 厘米,若将木块从容器中取出,水面将下降多少厘米?
答案:1厘米
巩固练习
练习10:如图,一个直圆柱形状的玻璃杯,将一个长为 12 厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内,当吸管端点接触圆柱下底面时,吸管最少可露出上底面边缘 2 厘米,最多能露出 4 厘米,则这个玻璃的容积为多少立方厘米?
答案:226.08立方厘米
圆柱的特征
可有长方形旋转得到;
两个底面,一个侧面,无数条高;
圆柱体积
剪拼法推导体积公式;
底面积×高=体积
圆柱表面积
侧面沿高展开是长方形;
两底面积加上侧面积得到表面积
课堂小结
课后作业
作业1:求下图的表面积和体积。(单位:厘米)
答案:
表面积:735.5平方厘米
体积:1392.5立方厘米
10
10
10
课后作业
作业2:一个圆柱形水杯,底面半径 5 厘米、高 8 厘米,在里面倒入 500 毫升水,再把一个棱长 6 厘米的正方体铁块放入水中,水会溢出多少毫升?
答案:88毫升
课后作业
作业3:底面直径是 4 厘米,高是 10 厘米的圆柱,分成两部分,求这两部分的体积比是多少?
答案:
7:3
课后作业
作业4:有一个圆柱体,高是底面半径的 3 倍,将它如图分成大、小两个圆柱体,大圆柱体的表面积是小圆柱体的 3 倍,求大小两个圆柱的体积比。
答案:
11:1
课后作业
作业5:如图,一个瓶子的瓶身呈圆柱形(不计瓶颈),瓶子高30厘米,瓶身的底面直径是 12 厘米,正放时,水面高度是 20 厘米,现将瓶子倒放,水面高度是25厘米,问瓶子里一共有多少升水?
答案:2.826升
心有花种,静候花开
下节课再见!
圆柱的认识
与计算
情境导入
嗨,我今天买了张海报,东77的~哈哈哈,打开给你瞧瞧
谁啊,不认识,没听过,又不是C罗,不看不看~
新知探究
我知道,就像我的保温杯一样~可以泡枸杞
超市旋转门貌似是这样子的,旋转门,当然是旋转啦~
同学们,今天我们认识下圆柱,大家说说它有什么特点
都说面动成体,怎么可以得到圆柱呢?
Good
新知探究
圆柱:是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体,它有 2 个大小相同、相互平行的圆形底面和 1 个曲面侧面。
两平行线之间的距离是平面图形的高,两平行面之间的距离是立体图形的高。
底面
底面
侧面
高
底面半径
这么说,圆柱有无数条高
数学例题
例题1:请在下图中标出相应位置的名称。
答案:
( )
( )
( )
( )
巩固练习
练习1:下图中,以直线为轴旋转一周,可以形成圆柱的是 ____________。
A. B. C. D.
答案:B
新知探究
我知道,两个圆,再加上侧面,可侧面咋算啊!
表面积,就是把圆柱的三个面的面积加起来
同学们,下面我们来研究下圆柱的表面积
有思路了吧?
新知探究
圆柱的表面积:圆柱的表面积包括上、下两个底面的面积和侧面面积,上、下两个底面是圆,侧面沿高展开是长方形,长方形的一边是底面周长,一边的高。
底面积:πr2
侧面积:2πrh
表面积:2πr2+2πrh
必须沿高展开,才能得到长方形
斜着剪开呢?
数学例题
例题2:
(1)一个圆柱的侧面展开后得到一个长方形,长是 12.56cm,宽是 3cm,这个圆柱的侧面积是 ____________cm2。
(2)一个圆柱的侧面展开后得到一个正方形,边长是 9.42cm,这个圆柱的底面周长是 ____________cm,高是 ____________cm。
答案:
(1)37.68
(2)9.42;9.42
巩固练习
练习2:一张长方形纸,长为 25cm,宽为 14cm.把这张长方形纸卷成一个圆柱体,这个圆柱体的底面周长是多少厘米?圆柱体的高是多少厘米?(接头处长度忽略不计)
答案:底面周长是25厘米,高14厘米或底面周长是14厘米,高25厘米
数学例题
例题3:一根长 1 米,横截面直径是 20 厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 ____________平方厘米。
答案:3454
巩固练习
练习3:一个圆柱分成相等的四个圆柱,表面积增加 18.84 平方分米,则圆柱的一个底面的面积是多少平方分米?
答案:6.28平方分米
数学例题
例题4:妙妙过生日的时候,妈妈给她买了一个豪华大蛋糕,总共有3层,每层都是圆柱形,每层高1分米,从上往下的半径分别是10厘米,20厘米,30厘米,求这个蛋糕的表面积是多少平方厘米?(包括最下层底面的面积)
答案:9420平方厘米
巩固练习
练习4:有一个圆柱体的零件,高 10 厘米,底面直径是 6 厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是 4 厘米,孔深 5 厘米(如图), 如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米 (π 取 3.14)
答案:307.72平方厘米
新知探究
我知道,圆柱的体积就是圆柱所占空间的大小!
体积都这样,问题是怎么算呢?
同学们,学习了表面积,下面该学习圆柱体积了
是不是很熟悉!
新知探究
圆柱的体积:类似于圆面积公式的推导方法,把圆柱分割成若干小份,拼成一个近似的长方体,圆柱的体积等于近似的长方体的体积。
长方体长→圆柱底面周长的一半(πr)
长方体宽→圆柱底面半径(r)
长方体高→圆柱高(h)
圆柱体积:πr×r×h=πr2h
πr2是圆柱底面积,那么圆柱体积也可以用“底面积×高”表示!
三棱柱、四棱柱、五棱柱、六棱柱、圆柱……体积都是这样算的!
数学例题
例题5:求下面圆柱的表面积和体积。(π 取 3.14)
答案:
图1:150.72平方厘米,141.3立方厘米
图2:113.04平方分米,87.92立方分米
3厘米
5厘米
7分米
2分米
巩固练习
练习5:一个圆柱形无盖的水桶,底面的直径是 6dm,高是 4dm,做这样一个水桶,需要多少平方分米的铁皮?它的容积是多少?(π 取 3.14)
答案:103.62平方厘米;113.04升
数学例题
例题6:一张长方形纸片,长 10 厘米,宽 4 厘米,以这个长方形的长或宽为轴,将这个长方形旋转 360度,可以得到两个不同的圆柱体,求这两个圆柱的表面积之比、体积之比的侧面积之比分别是多少?
答案:
表面积之比,5:2
体积之比,5:2
侧面积之比,1:1
巩固练习
练习6:现有长是 5 厘米,宽是 3 厘米的长方形,以下面的四种方式进行旋转,可以得到四个不同的圆柱,试判断哪种方式得到的圆柱体积最大。
答案:图3得到的体积最大
数学例题
例题7:一个圆柱的高增加 3 分米 , 表面积就增加 56.52 平方分米 , 它的体积增加多少立方分米
答案:84.78立方分米
巩固练习
练习7:一个圆柱被截去 5cm 后,圆柱的表面积减少了 62.8cm2,原来圆柱的表面积是多少平方厘米?
答案:276.32平方厘米
数学例题
例题8:一个圆柱体形状的木棒 , 沿着底面直径竖直切成两部分 ,已知这两部分的表面积之和比圆柱体的表面积大 2008cm2,则这个圆柱体木棒的侧面积是 ____________cm2 。(π 取 3.14)
答案:3152.56
巩固练习
练习8:如图,由底面半径是3分米的圆柱切割而成的不规则几何体,求这个几何体的体积?(π 取 3.14)
答案:197.82立方分米
8分米
6分米
数学例题
例题9:如图,一个瓶子的瓶身呈圆柱形(不计瓶颈),已知瓶内装有 1.6 升的水,当瓶子正放时瓶内水面高 12 厘米,当瓶子倒放时瓶内空余部分高 3 厘米,问瓶子的容积是多少升?
答案:2升
巩固练习
练习9:一个酒瓶里面深 30 厘米,底面内直径是 10 厘米,瓶里酒深 15 厘米,把酒瓶塞紧后使其瓶口向下倒立,这时酒深 25 厘米,酒瓶的容积是多少立方厘米?
答案:1570立方厘米
数学例题
例题10:如图,底面积为 50 平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为 5 厘米的正方体木块,木块浮出水面的高度是 3 厘米,若将木块从容器中取出,水面将下降多少厘米?
答案:1厘米
巩固练习
练习10:如图,一个直圆柱形状的玻璃杯,将一个长为 12 厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内,当吸管端点接触圆柱下底面时,吸管最少可露出上底面边缘 2 厘米,最多能露出 4 厘米,则这个玻璃的容积为多少立方厘米?
答案:226.08立方厘米
圆柱的特征
可有长方形旋转得到;
两个底面,一个侧面,无数条高;
圆柱体积
剪拼法推导体积公式;
底面积×高=体积
圆柱表面积
侧面沿高展开是长方形;
两底面积加上侧面积得到表面积
课堂小结
课后作业
作业1:求下图的表面积和体积。(单位:厘米)
答案:
表面积:735.5平方厘米
体积:1392.5立方厘米
10
10
10
课后作业
作业2:一个圆柱形水杯,底面半径 5 厘米、高 8 厘米,在里面倒入 500 毫升水,再把一个棱长 6 厘米的正方体铁块放入水中,水会溢出多少毫升?
答案:88毫升
课后作业
作业3:底面直径是 4 厘米,高是 10 厘米的圆柱,分成两部分,求这两部分的体积比是多少?
答案:
7:3
课后作业
作业4:有一个圆柱体,高是底面半径的 3 倍,将它如图分成大、小两个圆柱体,大圆柱体的表面积是小圆柱体的 3 倍,求大小两个圆柱的体积比。
答案:
11:1
课后作业
作业5:如图,一个瓶子的瓶身呈圆柱形(不计瓶颈),瓶子高30厘米,瓶身的底面直径是 12 厘米,正放时,水面高度是 20 厘米,现将瓶子倒放,水面高度是25厘米,问瓶子里一共有多少升水?
答案:2.826升
心有花种,静候花开
下节课再见!
