六年级下册数学课件-第5讲《圆锥的认识与计算》 人教版(共35张PPT)
文档属性
| 名称 | 六年级下册数学课件-第5讲《圆锥的认识与计算》 人教版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
圆锥的认识与计算
情境导入
我的甜筒好像跟大家的不一样!
新知探究
我知道,就像甜筒一样,我最喜欢了~
真是个吃货,蒙古包的屋顶,粮仓的上半部分~
同学们,前面我们认识了圆柱,今天我们认识下圆锥
没错,生活中有很多例子?
新知探究
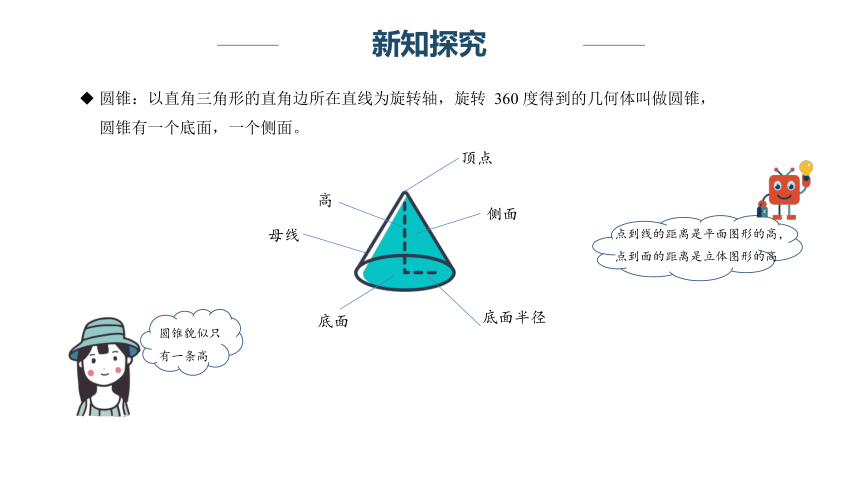
圆锥:以直角三角形的直角边所在直线为旋转轴,旋转 360 度得到的几何体叫做圆锥,圆锥有一个底面,一个侧面。
点到线的距离是平面图形的高,点到面的距离是立体图形的高
底面
顶点
侧面
高
底面半径
圆锥貌似只有一条高
母线
数学例题
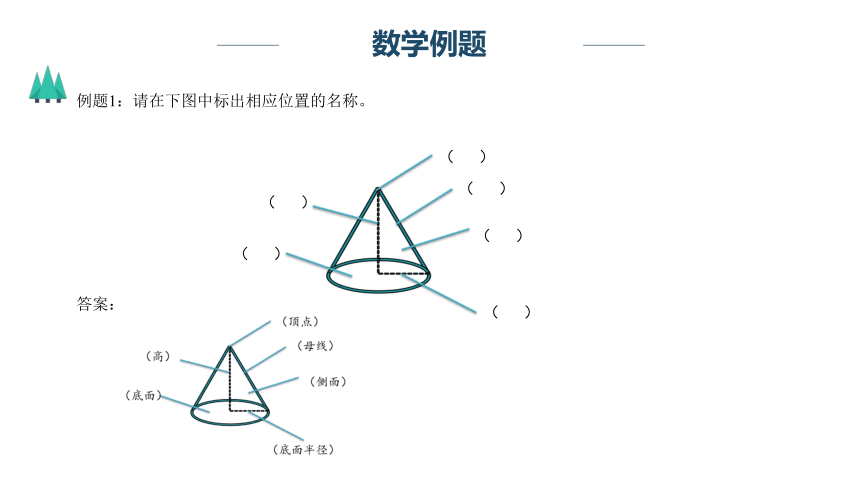
例题1:请在下图中标出相应位置的名称。
答案:
( )
( )
( )
( )
( )
( )
巩固练习
练习1:下面有关圆锥的说法正确的是 ____________。(填序号)
①圆锥和圆柱一样,都有无数条高
②从正面观察圆锥,可以得到一个等腰三角形
③圆锥沿高竖直切开,得到的截面是扇形
④圆锥沿高竖直切开,有可能得到一个等边三角形
⑤圆锥有无数条母线,但只有一条高
⑥从上面看,圆锥和圆柱得到的图形是一样的
⑦把圆锥水平切开,可以得到一个小圆锥和一个圆柱
⑧圆锥的高指的是顶点到底面的垂线段的长度
答案:②⑤⑧
新知探究
我也知道,问题是侧面咋算啊!
表面积,底面积加上侧面积就可以了~
同学们,你们知道圆锥的表面积怎么求吗?
其实也是展开
新知探究
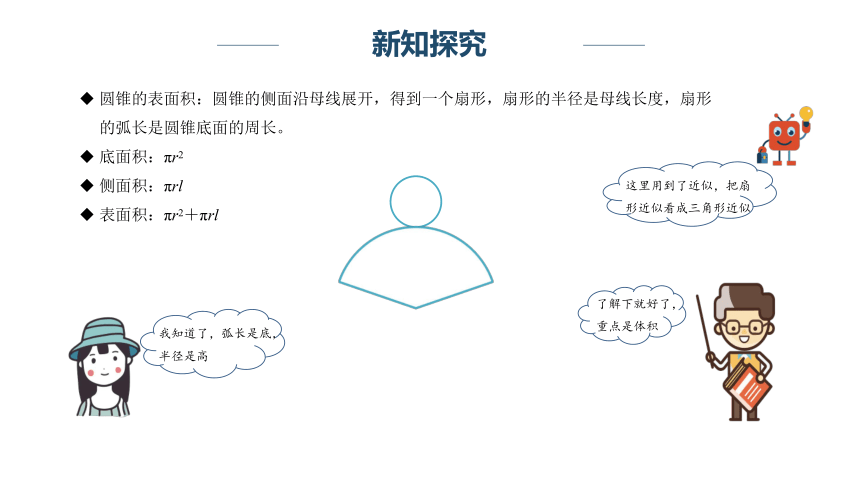
圆锥的表面积:圆锥的侧面沿母线展开,得到一个扇形,扇形的半径是母线长度,扇形的弧长是圆锥底面的周长。
底面积:πr2
侧面积:πrl
表面积:πr2+πrl
这里用到了近似,把扇形近似看成三角形近似
我知道了,弧长是底,半径是高
了解下就好了,重点是体积
数学例题
例题2:一个圆锥侧面沿母线展开后,得到一个半径是 5 厘米,弧长是 18.84 厘米的扇形,那么圆锥的底面积是多少平方厘米?表面积是多少平方厘米?
答案:28.26平方厘米;125.6平方厘米
巩固练习
练习2:底面半径是6厘米,高是8厘米的圆锥,侧面沿母线展开得到一个扇形,问这个扇形的半径是多少厘米?圆锥的侧面积是多少平方厘米?
答案:10厘米;188.4平方厘米
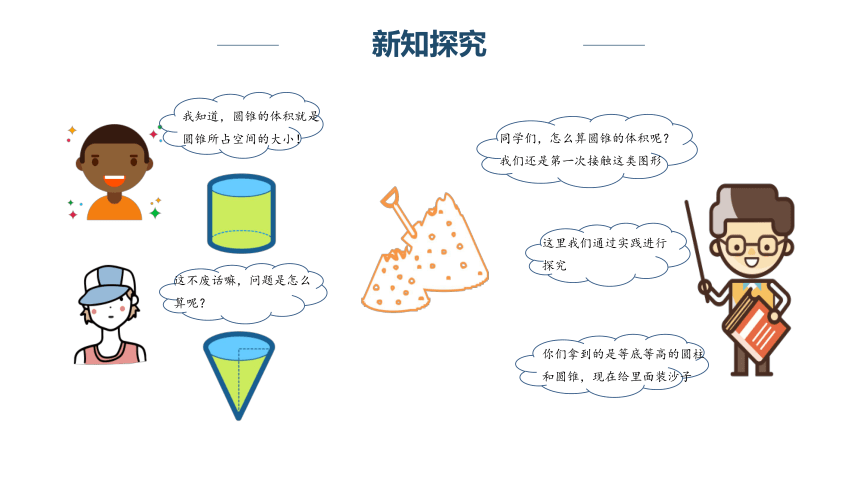
新知探究
我知道,圆锥的体积就是圆锥所占空间的大小!
这不废话嘛,问题是怎么算呢?
同学们,怎么算圆锥的体积呢?我们还是第一次接触这类图形
这里我们通过实践进行探究
你们拿到的是等底等高的圆柱和圆锥,现在给里面装沙子
新知探究
圆锥的体积:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的 3 倍;
圆柱体积:πr2h
圆锥体积:πr2h÷3
注意:必须是等底等高的圆柱和圆锥。
其它的椎体体积的计算方法是否跟圆锥一样,用“底面积×高÷3”表示呢!
三棱锥、四棱锥、五棱锥、六棱锥、圆锥……体积都是这样算的!
数学例题
例题3:计算下面图形的体积。(单位:分米)
答案:47.1立方分米;65.94立方分米
3
5
3
7
巩固练习
练习3:现有一个长、宽、高分别是20 厘米、15 厘米、15 厘米的长方体,现要把长方体削成一个体积最大的圆锥,问削去的部分是多少立方厘米?
答案:3322.5立方厘米
数学例题
例题4:等底等高的圆柱和圆锥,已知它们的体积之和是 144 立方分米,那么它们的体积之差是 ____________ 立方分米,圆锥的体积是 ____________ 立方分米,圆柱的体积是 ____________ 立方分米。
答案:72;36;108
巩固练习
练习4:体积相等的圆柱和圆锥,已知它们的底面半径之比是 2:3,那么圆柱与圆锥的高之比是多少?
数学例题
例题5:直角边长是 3 厘米和 4 厘米的直角三角形,以直角边为轴进行旋转,得到两个不同的圆锥,问这两个圆锥的体积比是多少?
答案:
4:3
巩固练习
练习5:直角边长是 6 厘米和 8 厘米的直角三角形,斜边是10厘米,以三条边为轴进行旋转,得到三个不同的几何体,问这三个几何体的体积比是多少?
答案:
20:15:12
数学例题
例题6:如图,直角三角形如果以BC边为轴旋转一周,那么所形成的圆锥的体积为 16π,以
AC边为轴旋转一周,那么所形成的圆锥的体积为 12π,那么如果以AB为轴旋转一周,那么所形成的几何体的体积是多少?(结果保留π)
答案:9.6π
A
C B
巩固练习
练习6:长方形ABCD中,长是 8 厘米,宽是 6 厘米,AC、BD为长方形的对角线,现以直线l为轴,旋转一周,问图中空白部分扫过的区域的体积是多少立方厘米?
答案:150.72立方厘米
A B
D C
l
数学例题
例题7:妙妙把一个高为 36 厘米圆锥形的木块模具截成完全一样的两部分,这样它的表面积增加 720 平方厘米,原来这块圆锥形模具的体积是多少?
答案:942立方厘米
巩固练习
练习7:有一个圆柱体木块,如果将这个圆柱体木块沿上下底面圆心切成同样的四块,表面积增加 120 平方厘米;若将这个圆柱体切成三个同样的小圆柱体,表面积增加 113.04 平方厘米,现在把这个圆柱体木块削成一个最大的圆锥体,要削去多少立方厘米的木料?
答案:94.2立方厘米
数学例题
例题8:如图,一个圆柱体容器中完全浸没甲、乙两个圆锥,已知甲、乙两个圆锥的底面积之比是 3:2,如果把甲、乙两个圆锥都拿出来,水面下降 3 厘米;如果只拿出甲圆锥,水面下降 2 厘米,若乙圆锥高为 2.4 厘米,则甲圆锥高是多少厘米?
答案:3.2厘米
巩固练习
练习8:如图,在长为 10 厘米,宽为 8 厘米的长方体容器内注入一些水,将等底等高的圆柱和圆锥浸没在水中,发水现面上升了 1 厘米(水未溢出),求圆柱和圆锥的体积分别为多少?
答案:60立方厘米,20立方厘米
数学例题
例题9:如图,甲、乙两容器相同,水面高度相同,问甲容器中水的体积是乙容器中水的体积的多少倍?
答案:19倍
巩固练习
练习9:如图,圆锥形容器中装有水 50 升,水面高度是圆锥高度的一半,这个容器最多能装水多少升?
答案:400升
圆锥的特点
可通过直角三角形旋转得到;
一个底面,一个侧面,一条高,无数条母线
圆锥的体积
圆锥体积是等底等高圆柱体积的三分之一;
等底等高是基本条件
圆锥的表面积
侧面沿母线展开是扇形,扇形弧长是底面周长;
底面积加上侧面积得到表面积
课堂小结
课后作业
作业1:如图,有一根长为 20 厘米,直径为 6 厘米的圆钢,在它的两端各钻一个 4厘米深,底面直径也为6厘米的圆锥形的孔,做成一个零件,这个零件的体积为多少立方厘米?(π 取 3.14)
答案:489.84立方厘米
课后作业
作业2:某商店用大号圆锥形纸筒盛装爆米花来卖,纸筒的高度为 15cm,底面半径 4cm,那么纸筒的体积是多少?如果一粒爆米花的平均体积是 0.4cm3,那么这个纸筒从体积看理论上可以装多少粒爆米花?实际上装得了吗,为什么?( π取 3.14)
答案:600粒,装不了
课后作业
作业3:等底等高的圆柱和圆锥,已知二者的体积之差是 72 立方分米,那么圆锥的体积是____________ 立方分米,圆柱的体积是____________ 立方分米,二者的体积之和是____________ 立方分米。
答案:36;108;144
课后作业
作业4:现有一个直角边长是 6 厘米和 8 厘米的直角三角形,以不同的边为轴进行旋转,可以得到不同的几何体,问怎样旋转,得到的几何体体积最大,最大的体积是多少?
答案:
以6厘米为轴,以8厘米为半径,得到的体积最大,最大体积是401.92立方厘米
6
8
10
课后作业
作业5:如图,一个圆锥的底面周长是 18.84 厘米,高是 6 厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来圆锥的表面积增加了多少平方厘米?
答案:72平方厘米
课后作业
作业6:李大爷将一些玉米堆放在室内的一个墙角(如图,墙面与墙面,墙面与地面之间的夹角均为直角),测得地面上A到B间的弧长为 3.14 米,A点和B点到墙角的距离相等,且这堆玉米的高为 1.5米,已知每立方米玉米约重 770千克,试估算这堆玉米的质量。
答案:1208.9千克
A
B
科普天地
圆锥曲线
圆锥曲线,是由一平面截二次锥面得到的曲线。圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线。
圆锥曲线又叫做二次曲线,圆锥曲线一直是几何学研究的重要课题之一,无论在数学以及其他科学技术领域,还是在我们的实际生活中都占有重要的地位,人们对它的研究也不断深化,其研究成果又广泛地得到应用,这正好反映了人们认识事物的目的和规律。
双曲线
抛物线
椭圆
圆
我决定找根萝卜实践一下
心有花种,静候花开
下节课再见!
圆锥的认识与计算
情境导入
我的甜筒好像跟大家的不一样!
新知探究
我知道,就像甜筒一样,我最喜欢了~
真是个吃货,蒙古包的屋顶,粮仓的上半部分~
同学们,前面我们认识了圆柱,今天我们认识下圆锥
没错,生活中有很多例子?
新知探究
圆锥:以直角三角形的直角边所在直线为旋转轴,旋转 360 度得到的几何体叫做圆锥,圆锥有一个底面,一个侧面。
点到线的距离是平面图形的高,点到面的距离是立体图形的高
底面
顶点
侧面
高
底面半径
圆锥貌似只有一条高
母线
数学例题
例题1:请在下图中标出相应位置的名称。
答案:
( )
( )
( )
( )
( )
( )
巩固练习
练习1:下面有关圆锥的说法正确的是 ____________。(填序号)
①圆锥和圆柱一样,都有无数条高
②从正面观察圆锥,可以得到一个等腰三角形
③圆锥沿高竖直切开,得到的截面是扇形
④圆锥沿高竖直切开,有可能得到一个等边三角形
⑤圆锥有无数条母线,但只有一条高
⑥从上面看,圆锥和圆柱得到的图形是一样的
⑦把圆锥水平切开,可以得到一个小圆锥和一个圆柱
⑧圆锥的高指的是顶点到底面的垂线段的长度
答案:②⑤⑧
新知探究
我也知道,问题是侧面咋算啊!
表面积,底面积加上侧面积就可以了~
同学们,你们知道圆锥的表面积怎么求吗?
其实也是展开
新知探究
圆锥的表面积:圆锥的侧面沿母线展开,得到一个扇形,扇形的半径是母线长度,扇形的弧长是圆锥底面的周长。
底面积:πr2
侧面积:πrl
表面积:πr2+πrl
这里用到了近似,把扇形近似看成三角形近似
我知道了,弧长是底,半径是高
了解下就好了,重点是体积
数学例题
例题2:一个圆锥侧面沿母线展开后,得到一个半径是 5 厘米,弧长是 18.84 厘米的扇形,那么圆锥的底面积是多少平方厘米?表面积是多少平方厘米?
答案:28.26平方厘米;125.6平方厘米
巩固练习
练习2:底面半径是6厘米,高是8厘米的圆锥,侧面沿母线展开得到一个扇形,问这个扇形的半径是多少厘米?圆锥的侧面积是多少平方厘米?
答案:10厘米;188.4平方厘米
新知探究
我知道,圆锥的体积就是圆锥所占空间的大小!
这不废话嘛,问题是怎么算呢?
同学们,怎么算圆锥的体积呢?我们还是第一次接触这类图形
这里我们通过实践进行探究
你们拿到的是等底等高的圆柱和圆锥,现在给里面装沙子
新知探究
圆锥的体积:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的 3 倍;
圆柱体积:πr2h
圆锥体积:πr2h÷3
注意:必须是等底等高的圆柱和圆锥。
其它的椎体体积的计算方法是否跟圆锥一样,用“底面积×高÷3”表示呢!
三棱锥、四棱锥、五棱锥、六棱锥、圆锥……体积都是这样算的!
数学例题
例题3:计算下面图形的体积。(单位:分米)
答案:47.1立方分米;65.94立方分米
3
5
3
7
巩固练习
练习3:现有一个长、宽、高分别是20 厘米、15 厘米、15 厘米的长方体,现要把长方体削成一个体积最大的圆锥,问削去的部分是多少立方厘米?
答案:3322.5立方厘米
数学例题
例题4:等底等高的圆柱和圆锥,已知它们的体积之和是 144 立方分米,那么它们的体积之差是 ____________ 立方分米,圆锥的体积是 ____________ 立方分米,圆柱的体积是 ____________ 立方分米。
答案:72;36;108
巩固练习
练习4:体积相等的圆柱和圆锥,已知它们的底面半径之比是 2:3,那么圆柱与圆锥的高之比是多少?
数学例题
例题5:直角边长是 3 厘米和 4 厘米的直角三角形,以直角边为轴进行旋转,得到两个不同的圆锥,问这两个圆锥的体积比是多少?
答案:
4:3
巩固练习
练习5:直角边长是 6 厘米和 8 厘米的直角三角形,斜边是10厘米,以三条边为轴进行旋转,得到三个不同的几何体,问这三个几何体的体积比是多少?
答案:
20:15:12
数学例题
例题6:如图,直角三角形如果以BC边为轴旋转一周,那么所形成的圆锥的体积为 16π,以
AC边为轴旋转一周,那么所形成的圆锥的体积为 12π,那么如果以AB为轴旋转一周,那么所形成的几何体的体积是多少?(结果保留π)
答案:9.6π
A
C B
巩固练习
练习6:长方形ABCD中,长是 8 厘米,宽是 6 厘米,AC、BD为长方形的对角线,现以直线l为轴,旋转一周,问图中空白部分扫过的区域的体积是多少立方厘米?
答案:150.72立方厘米
A B
D C
l
数学例题
例题7:妙妙把一个高为 36 厘米圆锥形的木块模具截成完全一样的两部分,这样它的表面积增加 720 平方厘米,原来这块圆锥形模具的体积是多少?
答案:942立方厘米
巩固练习
练习7:有一个圆柱体木块,如果将这个圆柱体木块沿上下底面圆心切成同样的四块,表面积增加 120 平方厘米;若将这个圆柱体切成三个同样的小圆柱体,表面积增加 113.04 平方厘米,现在把这个圆柱体木块削成一个最大的圆锥体,要削去多少立方厘米的木料?
答案:94.2立方厘米
数学例题
例题8:如图,一个圆柱体容器中完全浸没甲、乙两个圆锥,已知甲、乙两个圆锥的底面积之比是 3:2,如果把甲、乙两个圆锥都拿出来,水面下降 3 厘米;如果只拿出甲圆锥,水面下降 2 厘米,若乙圆锥高为 2.4 厘米,则甲圆锥高是多少厘米?
答案:3.2厘米
巩固练习
练习8:如图,在长为 10 厘米,宽为 8 厘米的长方体容器内注入一些水,将等底等高的圆柱和圆锥浸没在水中,发水现面上升了 1 厘米(水未溢出),求圆柱和圆锥的体积分别为多少?
答案:60立方厘米,20立方厘米
数学例题
例题9:如图,甲、乙两容器相同,水面高度相同,问甲容器中水的体积是乙容器中水的体积的多少倍?
答案:19倍
巩固练习
练习9:如图,圆锥形容器中装有水 50 升,水面高度是圆锥高度的一半,这个容器最多能装水多少升?
答案:400升
圆锥的特点
可通过直角三角形旋转得到;
一个底面,一个侧面,一条高,无数条母线
圆锥的体积
圆锥体积是等底等高圆柱体积的三分之一;
等底等高是基本条件
圆锥的表面积
侧面沿母线展开是扇形,扇形弧长是底面周长;
底面积加上侧面积得到表面积
课堂小结
课后作业
作业1:如图,有一根长为 20 厘米,直径为 6 厘米的圆钢,在它的两端各钻一个 4厘米深,底面直径也为6厘米的圆锥形的孔,做成一个零件,这个零件的体积为多少立方厘米?(π 取 3.14)
答案:489.84立方厘米
课后作业
作业2:某商店用大号圆锥形纸筒盛装爆米花来卖,纸筒的高度为 15cm,底面半径 4cm,那么纸筒的体积是多少?如果一粒爆米花的平均体积是 0.4cm3,那么这个纸筒从体积看理论上可以装多少粒爆米花?实际上装得了吗,为什么?( π取 3.14)
答案:600粒,装不了
课后作业
作业3:等底等高的圆柱和圆锥,已知二者的体积之差是 72 立方分米,那么圆锥的体积是____________ 立方分米,圆柱的体积是____________ 立方分米,二者的体积之和是____________ 立方分米。
答案:36;108;144
课后作业
作业4:现有一个直角边长是 6 厘米和 8 厘米的直角三角形,以不同的边为轴进行旋转,可以得到不同的几何体,问怎样旋转,得到的几何体体积最大,最大的体积是多少?
答案:
以6厘米为轴,以8厘米为半径,得到的体积最大,最大体积是401.92立方厘米
6
8
10
课后作业
作业5:如图,一个圆锥的底面周长是 18.84 厘米,高是 6 厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来圆锥的表面积增加了多少平方厘米?
答案:72平方厘米
课后作业
作业6:李大爷将一些玉米堆放在室内的一个墙角(如图,墙面与墙面,墙面与地面之间的夹角均为直角),测得地面上A到B间的弧长为 3.14 米,A点和B点到墙角的距离相等,且这堆玉米的高为 1.5米,已知每立方米玉米约重 770千克,试估算这堆玉米的质量。
答案:1208.9千克
A
B
科普天地
圆锥曲线
圆锥曲线,是由一平面截二次锥面得到的曲线。圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线。
圆锥曲线又叫做二次曲线,圆锥曲线一直是几何学研究的重要课题之一,无论在数学以及其他科学技术领域,还是在我们的实际生活中都占有重要的地位,人们对它的研究也不断深化,其研究成果又广泛地得到应用,这正好反映了人们认识事物的目的和规律。
双曲线
抛物线
椭圆
圆
我决定找根萝卜实践一下
心有花种,静候花开
下节课再见!
