人教版数学八年级下册18.1.2平行四边形的判定课后练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.1.2平行四边形的判定课后练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 637.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览




文档简介
18.1.2 平行四边形的判定 课后练习
一、单选题
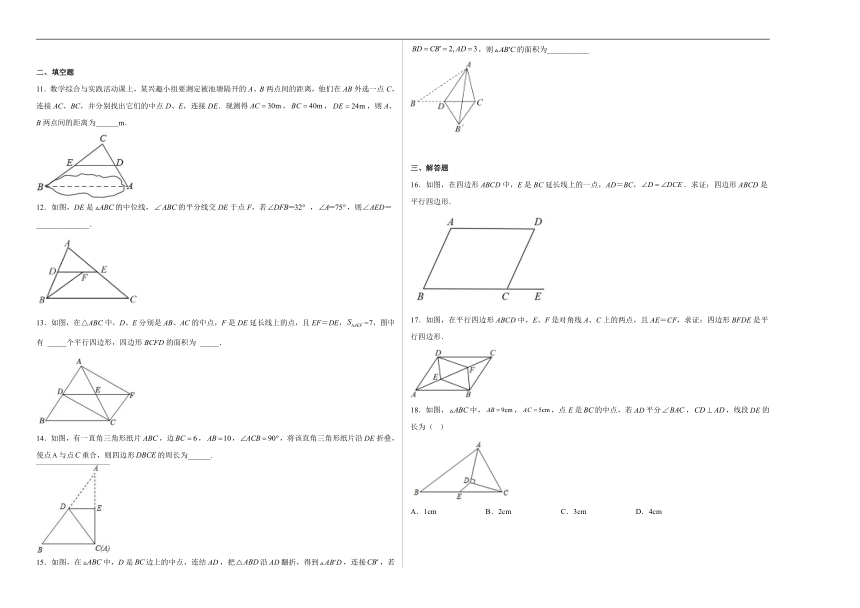
1.如图,点、分别是边、的中点,,则的长为( )
A. B. C. D.
2.在四边形中,对角线和交于点,下列条件不能判断四边形是平行四边形的是( )
A., B.,
C., D.,
3.如图,四边形中,点、、、分别是线段、、、的中点,则四边形的周长( )
A.只与、的长有关 B.只与、的长有关
C.只与、的长有关 D.与四边形各边的长都有关.
4.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B.10 C.12 D.14
5.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
6. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
7.如图,在 ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结若,,则的度数为
A. B. C. D.
8.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF
9.如图,在平行四边形中,过对角线上一点,作EFBC,HGAB,若四边形和四边形的面积分别为和,则与的大小关系为( )
A. B. C. D.不能确定
10.如图,分别以直角的斜边,直角边为边向外作等边和等边,为的中点,与交于点,与交于点,,.给出如下结论:①;②四边形为平行四边形;③;④;其中正确结论的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
11.数学综合与实践活动课上,某兴趣小组要测定被池塘隔开的A、B两点间的距离,他们在AB外选一点C,连接AC、BC,并分别找出它们的中点D、E,连接DE.现测得,,,则A、B两点间的距离为______m.
12.如图,DE是的中位线,的平分线交DE于点F,若 ,,则∠AED=______________.
13.如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,=7,图中有 _____个平行四边形,四边形BCFD的面积为 _____.
14.如图,有一直角三角形纸片,边,,,将该直角三角形纸片沿折叠,使点与点重合,则四边形的周长为______.
15.如图,在中,D是边上的中点,连结,把沿翻折,得到,连接,若,则的面积为___________
三、解答题
16.如图,在四边形ABCD中,E是BC延长线上的一点,AD=BC,.求证:四边形ABCD是平行四边形.
17.如图,在平行四边形ABCD中,E、F是对角线A、C上的两点,且AE=CF,求证:四边形BFDE是平行四边形.
18.如图,中,,,点E是的中点,若平分,,线段的长为( )
A.1cm B.2cm C.3cm D.4cm
参考答案
1.D
【详解】根据三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半,可求得 ,故选D.
2.D
【详解】A、根据对角线互相平分的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
B、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
C、根据一组对边相等且平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,故此选项不符合题意;
D、根据一组对边平行,另一组对边相等的四边形不能判定四边形ABCD是平行四边形,故此选项符合题意;
故选:D.
3.B
【详解】解:点、、、分别是线段、、、的中点,
则线段分别为、、、的中位线,
∴,
四边形的周长,只与、的长有关
故选:B
4.C
【详解】解:∵点D、E分别是边AB,BC的中点,
∴DE是三角形BC的中位线,AB=2BD,BC=2BE,
∴DE∥BC且
又∵AB=2BD,BC=2BE,
∴AB+BC+AC=2(BD+BE+DE),
即△ABC的周长是△DBE的周长的2倍,
∵△DBE的周长是6,
∴△ABC的周长是:6×2=12.
故选C.
5.C
【详解】解:选项A:三角形的两边之差小于第三边,故选项A正确,不符合题意;
选项B:三角形的中位线平行且等于第三边的一半,故选项B正确,不符合题意;
选项C:一个角的两边分别平行另一个角的两边,则这两个角相等或互补,故选项C不正确,是假命题,符合题意;
选项D:一组对边平行且相等的四边形是平行四边形,故选项D正确,不符合题意;
故选:C.
6.C
【详解】如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而可得△DAF≌△BCE,然后得出∠DFA=∠BEC,
∴∠AFE=∠CEF,
∴AF∥CE,
结合选项B可证明四边形AECF是平行四边形,故本选项不符合题意;
故选:C.
7.B .
【详解】,,
,
ABCD的对角线AC与BD相交于点O,E是边CD的中点,
是的中位线,
,
,
故选B.
8.B
【详解】A、如图,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,故不符合题意;
B、如图所示,AE=CF,不能得到四边形AECF是平行四边形,故符合题意;
C、如图,∵四边形ABCD是平行四边形,
∴OA=OC,
∵AF//CE,
∴∠FAO=∠ECO,
又∵∠AOF=∠COE,
∴△AOF≌△COE,
∴AF=CE,
∴四边形AECF是平行四边形,故不符合题意;
D、如图,∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,
∴△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴∠AEO=∠CFO,
∴AE//CF,
∴四边形AECF是平行四边形,故不符合题意,
故选B.
.
9.A
【详解】解:∵四边形ABCD是平行四边形,EFBC,HGAB,
∴AD=BC,AB=CD,ABGHCD,ADEFBC,
∴四边形GBEP、HPFD是平行四边形,
∵在△ABD和△CDB中,AB=CD,BD=BD,AD=BC,
∴△ABD≌△CDB,
∴;
同理可得:,,,
∴
即,也即.
故选A.
10.D
【详解】解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴∠AHE =90°,
∴EF⊥AC,故①正确,
∵EF⊥AC,
∴AH=CH,
∵F是AB的中点,
∴FH是△ABC的中位线,
∴HF=BC,
∵BC=AB,AB=BD,
∴FH=BD,
即BD =4FH,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴EF=AD,
∴四边形ADFE为平行四边形,故②说法正确;
∴AG=AF,
∴AG=AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故选:D.
11.48
【详解】、分别是、的中点,
是的中位线,
故答案为:48.
12.##41度
【详解】解:∵DE是的中位线,
∴,
∴,.
∵,
∴.
∵的平分线交DE于点F,
∴,
∴.
∵,
∴.
故答案为:.
13. 2 28
【详解】解:∵点E为AC中点,
∴AE=CE,
∵EF=DE,
∴四边形ADCF为平行四边形,
∴,则,CF=AD,
∵点D为AB中点,
∴AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形;
∵AD=BD,
∴和等底同高,
∴,
故答案为:2,28.
14.18.
【详解】∵沿DE折叠,使点A与点C重合,
∴AE=CE,AD=CD,∠DCE=∠A,
∴∠BCD=90°-∠DCE,
又∵∠B=90°-∠A,
∴∠B=∠BCD,
∴BD=CD=AD=AB=5,
∴DE为△ABC的中位线,
∴DE=BC=3,
∵BC=6,AB=10,∠ACB=90°,
∴AC=,
∴四边形DBCE的周长为:BD+DE+CE+BC=5+3+4+6=18.
故答案为18.
15.
【详解】解:如图,过点A作,交延长线于点H,过D作于点G,则,
∵D是边上的中点,
∴,
∵把沿翻折,得到,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴四边形是平行四边形,
∴,
∵,
∴,
∵是等边三角形,,
∴,
∴,
∴.
故答案为:
16.
【详解】∵
∴AD∥BC
∵AD=BC
∴四边形ABCD是平行四边形
17. .
【详解】证明:连接DB,交AC于点O,
∵四边形ABCD是平行四边形,
∴AO=CO,DO=BO,
又∵AE=CF,
∴EO=FO,
∴四边形BFDE是平行四边形.
18.B
【详解】解:如图,延长交于F,
平分,
,
,
,
在和中,
,
(ASA),
, ,
,
又点E为的中点,
是的中位线,
.
故选:B.
一、单选题
1.如图,点、分别是边、的中点,,则的长为( )
A. B. C. D.
2.在四边形中,对角线和交于点,下列条件不能判断四边形是平行四边形的是( )
A., B.,
C., D.,
3.如图,四边形中,点、、、分别是线段、、、的中点,则四边形的周长( )
A.只与、的长有关 B.只与、的长有关
C.只与、的长有关 D.与四边形各边的长都有关.
4.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B.10 C.12 D.14
5.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
6. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
7.如图,在 ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结若,,则的度数为
A. B. C. D.
8.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF
9.如图,在平行四边形中,过对角线上一点,作EFBC,HGAB,若四边形和四边形的面积分别为和,则与的大小关系为( )
A. B. C. D.不能确定
10.如图,分别以直角的斜边,直角边为边向外作等边和等边,为的中点,与交于点,与交于点,,.给出如下结论:①;②四边形为平行四边形;③;④;其中正确结论的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
11.数学综合与实践活动课上,某兴趣小组要测定被池塘隔开的A、B两点间的距离,他们在AB外选一点C,连接AC、BC,并分别找出它们的中点D、E,连接DE.现测得,,,则A、B两点间的距离为______m.
12.如图,DE是的中位线,的平分线交DE于点F,若 ,,则∠AED=______________.
13.如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,=7,图中有 _____个平行四边形,四边形BCFD的面积为 _____.
14.如图,有一直角三角形纸片,边,,,将该直角三角形纸片沿折叠,使点与点重合,则四边形的周长为______.
15.如图,在中,D是边上的中点,连结,把沿翻折,得到,连接,若,则的面积为___________
三、解答题
16.如图,在四边形ABCD中,E是BC延长线上的一点,AD=BC,.求证:四边形ABCD是平行四边形.
17.如图,在平行四边形ABCD中,E、F是对角线A、C上的两点,且AE=CF,求证:四边形BFDE是平行四边形.
18.如图,中,,,点E是的中点,若平分,,线段的长为( )
A.1cm B.2cm C.3cm D.4cm
参考答案
1.D
【详解】根据三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半,可求得 ,故选D.
2.D
【详解】A、根据对角线互相平分的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
B、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
C、根据一组对边相等且平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,故此选项不符合题意;
D、根据一组对边平行,另一组对边相等的四边形不能判定四边形ABCD是平行四边形,故此选项符合题意;
故选:D.
3.B
【详解】解:点、、、分别是线段、、、的中点,
则线段分别为、、、的中位线,
∴,
四边形的周长,只与、的长有关
故选:B
4.C
【详解】解:∵点D、E分别是边AB,BC的中点,
∴DE是三角形BC的中位线,AB=2BD,BC=2BE,
∴DE∥BC且
又∵AB=2BD,BC=2BE,
∴AB+BC+AC=2(BD+BE+DE),
即△ABC的周长是△DBE的周长的2倍,
∵△DBE的周长是6,
∴△ABC的周长是:6×2=12.
故选C.
5.C
【详解】解:选项A:三角形的两边之差小于第三边,故选项A正确,不符合题意;
选项B:三角形的中位线平行且等于第三边的一半,故选项B正确,不符合题意;
选项C:一个角的两边分别平行另一个角的两边,则这两个角相等或互补,故选项C不正确,是假命题,符合题意;
选项D:一组对边平行且相等的四边形是平行四边形,故选项D正确,不符合题意;
故选:C.
6.C
【详解】如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而可得△DAF≌△BCE,然后得出∠DFA=∠BEC,
∴∠AFE=∠CEF,
∴AF∥CE,
结合选项B可证明四边形AECF是平行四边形,故本选项不符合题意;
故选:C.
7.B .
【详解】,,
,
ABCD的对角线AC与BD相交于点O,E是边CD的中点,
是的中位线,
,
,
故选B.
8.B
【详解】A、如图,∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,故不符合题意;
B、如图所示,AE=CF,不能得到四边形AECF是平行四边形,故符合题意;
C、如图,∵四边形ABCD是平行四边形,
∴OA=OC,
∵AF//CE,
∴∠FAO=∠ECO,
又∵∠AOF=∠COE,
∴△AOF≌△COE,
∴AF=CE,
∴四边形AECF是平行四边形,故不符合题意;
D、如图,∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,
∴△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴∠AEO=∠CFO,
∴AE//CF,
∴四边形AECF是平行四边形,故不符合题意,
故选B.
.
9.A
【详解】解:∵四边形ABCD是平行四边形,EFBC,HGAB,
∴AD=BC,AB=CD,ABGHCD,ADEFBC,
∴四边形GBEP、HPFD是平行四边形,
∵在△ABD和△CDB中,AB=CD,BD=BD,AD=BC,
∴△ABD≌△CDB,
∴;
同理可得:,,,
∴
即,也即.
故选A.
10.D
【详解】解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴∠AHE =90°,
∴EF⊥AC,故①正确,
∵EF⊥AC,
∴AH=CH,
∵F是AB的中点,
∴FH是△ABC的中位线,
∴HF=BC,
∵BC=AB,AB=BD,
∴FH=BD,
即BD =4FH,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴EF=AD,
∴四边形ADFE为平行四边形,故②说法正确;
∴AG=AF,
∴AG=AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故选:D.
11.48
【详解】、分别是、的中点,
是的中位线,
故答案为:48.
12.##41度
【详解】解:∵DE是的中位线,
∴,
∴,.
∵,
∴.
∵的平分线交DE于点F,
∴,
∴.
∵,
∴.
故答案为:.
13. 2 28
【详解】解:∵点E为AC中点,
∴AE=CE,
∵EF=DE,
∴四边形ADCF为平行四边形,
∴,则,CF=AD,
∵点D为AB中点,
∴AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形;
∵AD=BD,
∴和等底同高,
∴,
故答案为:2,28.
14.18.
【详解】∵沿DE折叠,使点A与点C重合,
∴AE=CE,AD=CD,∠DCE=∠A,
∴∠BCD=90°-∠DCE,
又∵∠B=90°-∠A,
∴∠B=∠BCD,
∴BD=CD=AD=AB=5,
∴DE为△ABC的中位线,
∴DE=BC=3,
∵BC=6,AB=10,∠ACB=90°,
∴AC=,
∴四边形DBCE的周长为:BD+DE+CE+BC=5+3+4+6=18.
故答案为18.
15.
【详解】解:如图,过点A作,交延长线于点H,过D作于点G,则,
∵D是边上的中点,
∴,
∵把沿翻折,得到,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴四边形是平行四边形,
∴,
∵,
∴,
∵是等边三角形,,
∴,
∴,
∴.
故答案为:
16.
【详解】∵
∴AD∥BC
∵AD=BC
∴四边形ABCD是平行四边形
17. .
【详解】证明:连接DB,交AC于点O,
∵四边形ABCD是平行四边形,
∴AO=CO,DO=BO,
又∵AE=CF,
∴EO=FO,
∴四边形BFDE是平行四边形.
18.B
【详解】解:如图,延长交于F,
平分,
,
,
,
在和中,
,
(ASA),
, ,
,
又点E为的中点,
是的中位线,
.
故选:B.
