人教版数学八年级下册18.2.1矩形 课后练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.2.1矩形 课后练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 813.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 09:10:59 | ||
图片预览



文档简介
18.2.1 矩形 课后练习
一、单选题
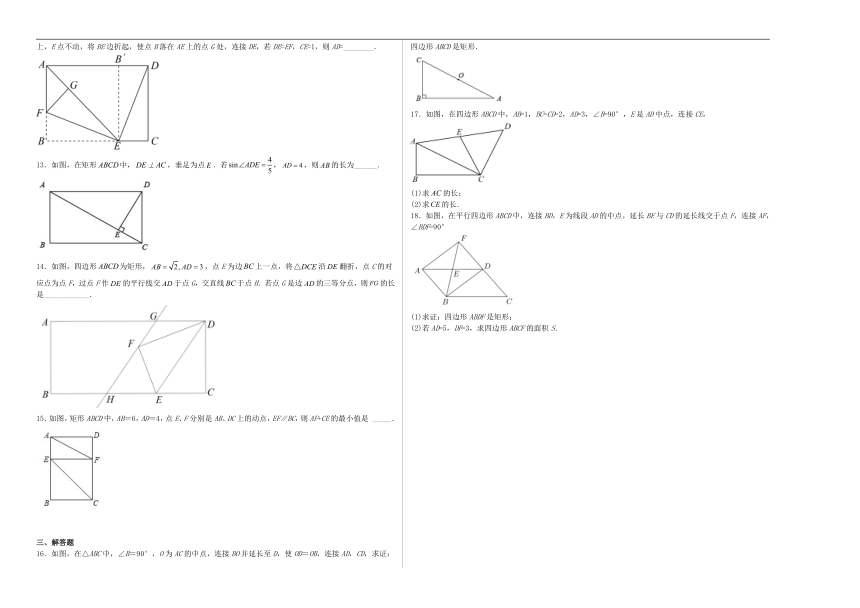
1.如图,O是矩形的对角线的中点,E是边的中点.若,则线段的长为( )
A.3 B.4 C.5 D.6
2.在直角三角形中,若斜边上的中线长为6,则斜边长为( )
A.12 B.6 C.3 D.4
3.如图,把矩形OABC放入平面直角坐标系中,点B的坐标为(10,8),点D是OC上一点,将△BCD沿BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
A.(0,4) B.(0,5)
C.(0,3) D.(0,2)
4.如图,在中,,点D,E分别为边BC,AC的中点,延长DE至点F,且,则四边形ADCF一定是( )
A.对角线互相垂直的四边形 B.菱形
C.正方形 D.矩形
5.将直角三角形纸片和矩形纸片按如图方式折叠放在一起,若∠1=51°,则∠2的度数为( )
A.51° B.39° C.49° D.32°
6.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
7.如图,在等边的,边上各取一点,,使,,相交于,若,则点到的距离等于( )
A.1 B.2 C. D.
8.在中,对角线,相交于点,只需添加一个条件,即可证明是矩形,这个条件可以是( )
A. B. C. D.
9.如图,在矩形ABCD中,AB=4cm,对角线AC与BD相交于点O,DE⊥AC,垂足为E,AE=3CE,则DE的长为( )
A. B.2cm C. D.
10.如图,在中,,平分交与点G,平分交于点D,、相交于点F,交的延长线于点E,连接,下列结论中正确的是( )
①若,则;②;③;④.
A.4个 B.3个 C.2个 D.1个
二、填空题
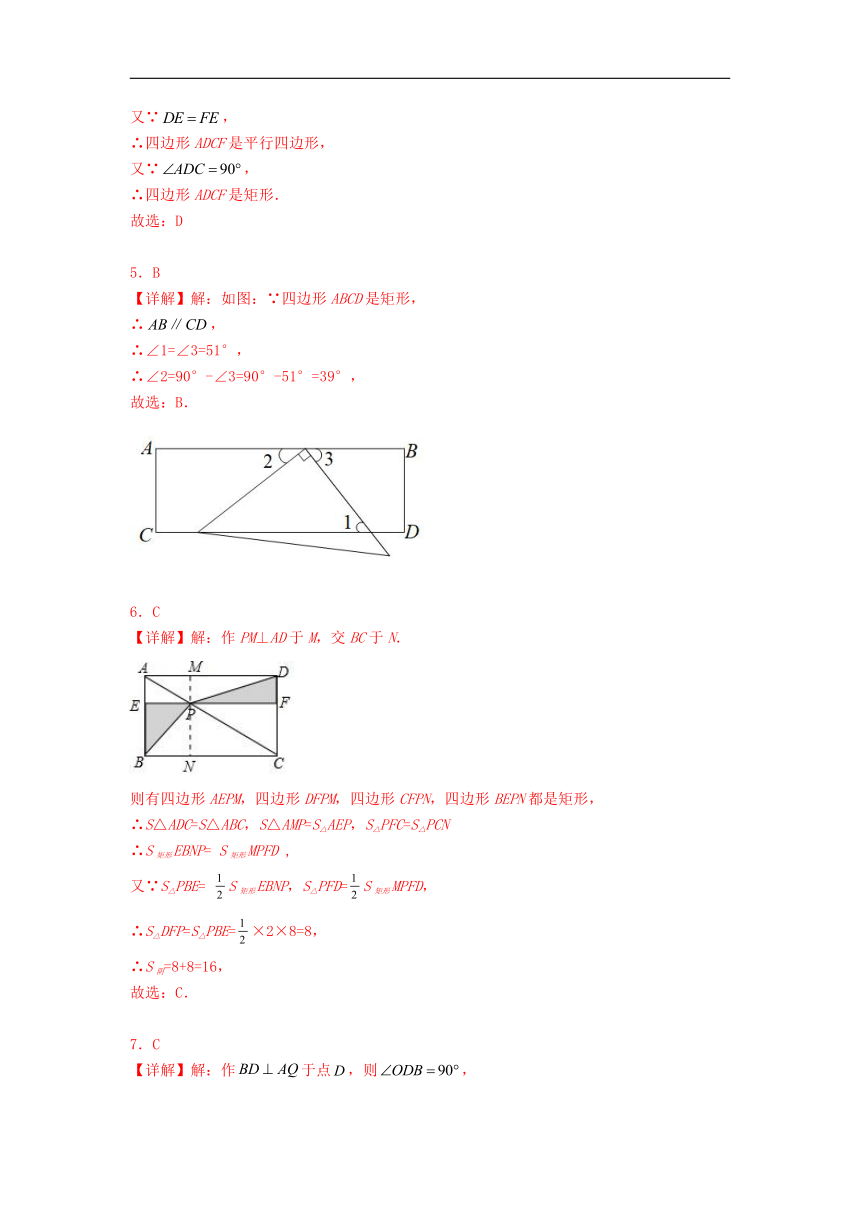
11.在中,是斜边上的中线,如果,那么______.
12.如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD=________.
13.如图,在矩形中,,垂足为点.若,,则的长为______.
14.如图,四边形为矩形,,点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是____________.
15.如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 _____.
三、解答题
16.如图,在△ABC中,∠B=90°,O为AC的中点,连接BO并延长至D,使OD=OB,连接AD,CD,求证:四边形ABCD是矩形.
17.如图,在四边形ABCD中,AB=1,BC=CD=2,AD=3,∠B=90°,E是AD中点,连接CE,
(1)求的长;
(2)求的长.
18.如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
参考答案
1.C
【详解】解:∵在矩形ABCD中,,,O是矩形ABCD的对角线BD的中点,E是AB边的中点,
∴OE为的中位线,
∴,,
∴,
∵点O为BD的中点,,
∴,
故选:C.
2.A
【详解】解:在直角三角形中,若斜边上的中线长为6,
该直角三角形斜边长为12,
故选:A.
3.C
【详解】解:∵点B的坐标为(10,8),
∴AO=BC=10,AB=OC=8,
由折叠的性质,可得:DE=CD,BE=BC=10,
在中,由勾股定理得:,
∴OE=AO-AE=10-6=4,
设OD=x,则DE=CD=8-x,
在中,由勾股定理得:,
即:,
解得:,
∴OD=3,
∴点D的坐标是(0,3).
故选:C.
4.D
【详解】解:∵,点D为BC的中点,
∴,即,
∵E为AC的中点,
∴,
又∵,
∴四边形ADCF是平行四边形,
又∵,
∴四边形ADCF是矩形.
故选:D
5.B
【详解】解:如图:∵四边形ABCD是矩形,
∴,
∴∠1=∠3=51°,
∴∠2=90°-∠3=90°-51°=39°,
故选:B.
6.C
【详解】解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PFC=S△PCN
∴S矩形EBNP= S矩形MPFD ,
又∵S△PBE= S矩形EBNP,S△PFD=S矩形MPFD,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故选:C.
7.C
【详解】解:作于点,则,
是等边三角形,
,,
在和中,
,
,
,
,
,
,
,
,
点到的距离等于,
故选:C.
8.B
【详解】∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是菱形,故A不符合题意;
∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是矩形,故B符合题意;
∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是菱形,故C不符合题意;
∵四边形ABCD是平行四边形,,
∴不能判定平行四边形ABCD是矩形,故D不符合题意;
故选B.
9.D
【详解】∵四边形ABCD是矩形,
∴OA=AC,OD=BD,AC=BD,CD=AB=4cm,
∴OA=OD=OC,
∵DE⊥AC,AE=3CE,
∴OE=CE,∠DEA=90°,
∴OD=CD=4cm,
∴OC=OD=CD=4cm,
∴OE=CE=2cm
∴
故选:D.
10.B
【详解】解:①∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
故①正确;
②∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
故②正确;
③如图,延长,交于点H,
∵,
∴,
∴,
∴点E为线段中点,
∴只有当时,
,
由题意得,
∴,
故③错误;
④如图,在上截取,连接,
∵,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
故④正确.
故选:B
11.
【详解】解:∵在中,是斜边上的中线,
∴,
∴,
故答案为:.
12.##
【详解】解:由翻折的性质可知,EB=EB′,∠B=∠AB′E=∠EB′D=90°,
在Rt△EBF和Rt△EB′D中,,
∴Rt△EBF≌Rt△EB′D(HL),
∴BF=DB′,
∵四边形ABCD是矩形,
∴∠C=∠CDB′=∠EB′D=90°,
∴四边形ECDB′是矩形,
∴DB′=EC=1,
∴BF=EC=1,
由翻折的性质可知,BF=FG=1,∠FAG=45°,∠EGF=∠B=∠AGF=90°,
∴AG=FG=1,
∴AF=.
∴AB=AB′=1+,
∴AD=AB′+DB′=2+,
故答案为:2+.
13.3
【详解】解:在中,
在矩形中,
故答案为:3.
14.或
【详解】①如图,过点作于点,
,
四边形是平行四边形
折叠
即
,
四边形是矩形
中,
,
中,
②如图,当时,
同理可得,
,
,
中,
故答案为:或
15.10
【详解】解:延长BC到G,使CG=EF,连接FG,
∵,EF=CG,
∴四边形EFGC是平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,
∴当点A、F、G三点共线时,AF+CE的值最小为AG,
由勾股定理得,AG===10,
∴AF+CE的最小值为10,
故答案为:10.
16.
【详解】证明:如图,
∵O为AC的中点,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
17.(1)AC=;
(2)CE=
【详解】(1)解:∵∠B=90°,AB=2,BC=1,
∴,
∴AC=(负值已舍);
(2)解:∵△ACD中,AC=,CD=2,AD=3,
∴=5+4=9,=9,
∴,
∴△ACD是直角三角形,且∠ACD=90°,
∵E是AD中点,
∴CE=AD=.
18.(1)见解析;
(2)18.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CF,
∴∠BAE=∠FDE,
∵E为线段AD的中点,
∴AE=DE,
又∵∠AEB=∠DEF,
∴≌(ASA),
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF是平行四边形,
∵∠BDF=90°,
∴四边形ABDF是矩形;
(2)解:由(1)知,四边形ABDF是矩形,
∴AB=DF=3,∠AFD=90°,
∴在中,,
∵四边形ABCD是平行四边形,
∴AB=CD=3,
∴CF=CD+DF=3+3=6,
∴.
一、单选题
1.如图,O是矩形的对角线的中点,E是边的中点.若,则线段的长为( )
A.3 B.4 C.5 D.6
2.在直角三角形中,若斜边上的中线长为6,则斜边长为( )
A.12 B.6 C.3 D.4
3.如图,把矩形OABC放入平面直角坐标系中,点B的坐标为(10,8),点D是OC上一点,将△BCD沿BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
A.(0,4) B.(0,5)
C.(0,3) D.(0,2)
4.如图,在中,,点D,E分别为边BC,AC的中点,延长DE至点F,且,则四边形ADCF一定是( )
A.对角线互相垂直的四边形 B.菱形
C.正方形 D.矩形
5.将直角三角形纸片和矩形纸片按如图方式折叠放在一起,若∠1=51°,则∠2的度数为( )
A.51° B.39° C.49° D.32°
6.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
7.如图,在等边的,边上各取一点,,使,,相交于,若,则点到的距离等于( )
A.1 B.2 C. D.
8.在中,对角线,相交于点,只需添加一个条件,即可证明是矩形,这个条件可以是( )
A. B. C. D.
9.如图,在矩形ABCD中,AB=4cm,对角线AC与BD相交于点O,DE⊥AC,垂足为E,AE=3CE,则DE的长为( )
A. B.2cm C. D.
10.如图,在中,,平分交与点G,平分交于点D,、相交于点F,交的延长线于点E,连接,下列结论中正确的是( )
①若,则;②;③;④.
A.4个 B.3个 C.2个 D.1个
二、填空题
11.在中,是斜边上的中线,如果,那么______.
12.如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD=________.
13.如图,在矩形中,,垂足为点.若,,则的长为______.
14.如图,四边形为矩形,,点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是____________.
15.如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是 _____.
三、解答题
16.如图,在△ABC中,∠B=90°,O为AC的中点,连接BO并延长至D,使OD=OB,连接AD,CD,求证:四边形ABCD是矩形.
17.如图,在四边形ABCD中,AB=1,BC=CD=2,AD=3,∠B=90°,E是AD中点,连接CE,
(1)求的长;
(2)求的长.
18.如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
参考答案
1.C
【详解】解:∵在矩形ABCD中,,,O是矩形ABCD的对角线BD的中点,E是AB边的中点,
∴OE为的中位线,
∴,,
∴,
∵点O为BD的中点,,
∴,
故选:C.
2.A
【详解】解:在直角三角形中,若斜边上的中线长为6,
该直角三角形斜边长为12,
故选:A.
3.C
【详解】解:∵点B的坐标为(10,8),
∴AO=BC=10,AB=OC=8,
由折叠的性质,可得:DE=CD,BE=BC=10,
在中,由勾股定理得:,
∴OE=AO-AE=10-6=4,
设OD=x,则DE=CD=8-x,
在中,由勾股定理得:,
即:,
解得:,
∴OD=3,
∴点D的坐标是(0,3).
故选:C.
4.D
【详解】解:∵,点D为BC的中点,
∴,即,
∵E为AC的中点,
∴,
又∵,
∴四边形ADCF是平行四边形,
又∵,
∴四边形ADCF是矩形.
故选:D
5.B
【详解】解:如图:∵四边形ABCD是矩形,
∴,
∴∠1=∠3=51°,
∴∠2=90°-∠3=90°-51°=39°,
故选:B.
6.C
【详解】解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PFC=S△PCN
∴S矩形EBNP= S矩形MPFD ,
又∵S△PBE= S矩形EBNP,S△PFD=S矩形MPFD,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故选:C.
7.C
【详解】解:作于点,则,
是等边三角形,
,,
在和中,
,
,
,
,
,
,
,
,
点到的距离等于,
故选:C.
8.B
【详解】∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是菱形,故A不符合题意;
∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是矩形,故B符合题意;
∵四边形ABCD是平行四边形,,
∴平行四边形ABCD是菱形,故C不符合题意;
∵四边形ABCD是平行四边形,,
∴不能判定平行四边形ABCD是矩形,故D不符合题意;
故选B.
9.D
【详解】∵四边形ABCD是矩形,
∴OA=AC,OD=BD,AC=BD,CD=AB=4cm,
∴OA=OD=OC,
∵DE⊥AC,AE=3CE,
∴OE=CE,∠DEA=90°,
∴OD=CD=4cm,
∴OC=OD=CD=4cm,
∴OE=CE=2cm
∴
故选:D.
10.B
【详解】解:①∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
故①正确;
②∵,
∴,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
故②正确;
③如图,延长,交于点H,
∵,
∴,
∴,
∴点E为线段中点,
∴只有当时,
,
由题意得,
∴,
故③错误;
④如图,在上截取,连接,
∵,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
故④正确.
故选:B
11.
【详解】解:∵在中,是斜边上的中线,
∴,
∴,
故答案为:.
12.##
【详解】解:由翻折的性质可知,EB=EB′,∠B=∠AB′E=∠EB′D=90°,
在Rt△EBF和Rt△EB′D中,,
∴Rt△EBF≌Rt△EB′D(HL),
∴BF=DB′,
∵四边形ABCD是矩形,
∴∠C=∠CDB′=∠EB′D=90°,
∴四边形ECDB′是矩形,
∴DB′=EC=1,
∴BF=EC=1,
由翻折的性质可知,BF=FG=1,∠FAG=45°,∠EGF=∠B=∠AGF=90°,
∴AG=FG=1,
∴AF=.
∴AB=AB′=1+,
∴AD=AB′+DB′=2+,
故答案为:2+.
13.3
【详解】解:在中,
在矩形中,
故答案为:3.
14.或
【详解】①如图,过点作于点,
,
四边形是平行四边形
折叠
即
,
四边形是矩形
中,
,
中,
②如图,当时,
同理可得,
,
,
中,
故答案为:或
15.10
【详解】解:延长BC到G,使CG=EF,连接FG,
∵,EF=CG,
∴四边形EFGC是平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,
∴当点A、F、G三点共线时,AF+CE的值最小为AG,
由勾股定理得,AG===10,
∴AF+CE的最小值为10,
故答案为:10.
16.
【详解】证明:如图,
∵O为AC的中点,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
17.(1)AC=;
(2)CE=
【详解】(1)解:∵∠B=90°,AB=2,BC=1,
∴,
∴AC=(负值已舍);
(2)解:∵△ACD中,AC=,CD=2,AD=3,
∴=5+4=9,=9,
∴,
∴△ACD是直角三角形,且∠ACD=90°,
∵E是AD中点,
∴CE=AD=.
18.(1)见解析;
(2)18.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CF,
∴∠BAE=∠FDE,
∵E为线段AD的中点,
∴AE=DE,
又∵∠AEB=∠DEF,
∴≌(ASA),
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF是平行四边形,
∵∠BDF=90°,
∴四边形ABDF是矩形;
(2)解:由(1)知,四边形ABDF是矩形,
∴AB=DF=3,∠AFD=90°,
∴在中,,
∵四边形ABCD是平行四边形,
∴AB=CD=3,
∴CF=CD+DF=3+3=6,
∴.
