2022-2023学年苏科版数学七年级下册第7章 平面图形的认识(二)(练习题)(无答案)
文档属性
| 名称 | 2022-2023学年苏科版数学七年级下册第7章 平面图形的认识(二)(练习题)(无答案) | 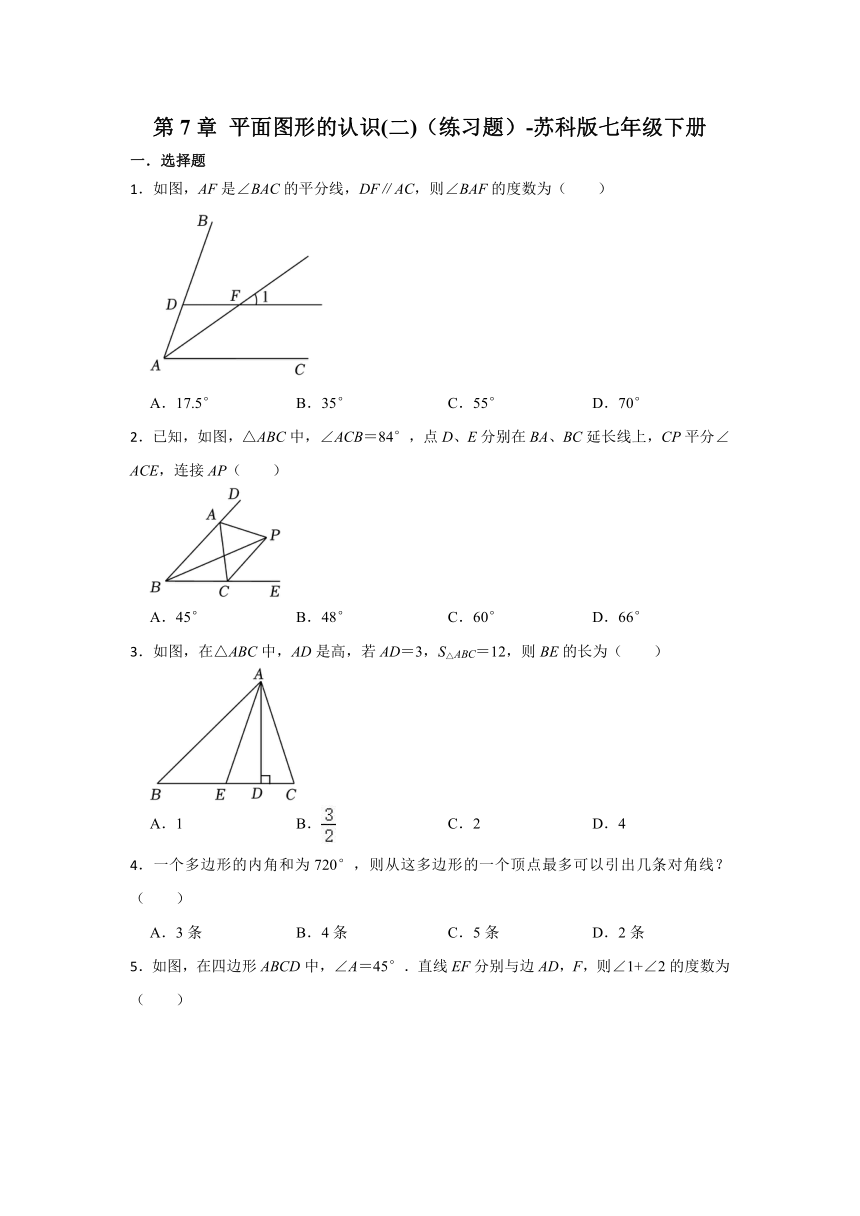 | |
| 格式 | docx | ||
| 文件大小 | 313.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 19:36:21 | ||
图片预览


文档简介
第7章 平面图形的认识(二)(练习题)-苏科版七年级下册
一.选择题
.如图,AF是∠BAC的平分线,DF∥AC,则∠BAF的度数为( )
A.17.5° B.35° C.55° D.70°
.已知,如图,△ABC中,∠ACB=84°,点D、E分别在BA、BC延长线上,CP平分∠ACE,连接AP( )
A.45° B.48° C.60° D.66°
.如图,在△ABC中,AD是高,若AD=3,S△ABC=12,则BE的长为( )
A.1 B. C.2 D.4
.一个多边形的内角和为720°,则从这多边形的一个顶点最多可以引出几条对角线?( )
A.3条 B.4条 C.5条 D.2条
.如图,在四边形ABCD中,∠A=45°.直线EF分别与边AD,F,则∠1+∠2的度数为( )
A.245° B.225° C.145° D.135°
.下列说法正确的是( )
A.若AC=BC,则点C是线段AB的中点
B.30.15°=30°15′
C.若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多形是九边形
D.钟表上的时间是11点10分,此时时针与分针所成的夹角是85°
.王师傅想做一个三角形的框架,他有两根长度分别为8cm和10cm的细木条,需要将其中一根木条分为两段,那么他可以把细木条分为两截的是( )
A.8cm的木条 B.10cm的木条 C.两根都可以 D.两根都不行
.如图,在六边形ABCDEF中,若∠1+∠2=85°( )
A.180° B.245° C.275° D.300°
.已知三角形的三边长分别是4,8,a+1,则a的取值可能是( )
A.10 B.11 C.12 D.13
.如图所示,∠ACB=∠DCE=90°.则下列结论:
①∠1=∠3;
②∠2+∠BCE=180°;
③若AB∥CE,则∠2=∠E;
④若∠2=∠B,则∠4=∠E.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
.如图,在三角形ABE中,点D为BE上一点,连接CD,若∠A=70°,则∠BDC= °.
.如果从多边形的一个顶点出发作它的对角线,能将多边形分成10个三角形,那么这个多边形是 边形.
.正六边形的一个内角是正n边形一个外角的5倍,则n等于 .
.如图,三角形ABC的周长为8cm,D为边AC上一点,则五边形ABCGE的周长为 .
.如图所示的是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=10cm,BE=6cm,则图中阴影部分面积为 .
三.解答题
.如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,你是如何思考的?
.如图,已知∠1+∠2=180°,∠DEF=∠A,
求证:
(1)EF∥AB.
(2)∠ACB=∠DEB.
.(1)问题发现:如图①,直线AB∥CD,连结BE,可以发现∠BEC=∠B+∠C.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∴∠B=∠BEF( ).
∵AB∥DC(已知),EF∥AB,
∴EF∥DC( ).
∴∠C=∠CEF.
∵( )=∠BEF+∠CEF,
∴∠BEC=∠B+∠C.(等量代换).
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C=360°﹣∠BEC.
(3)解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,∠2,∠3,∠5之间的数量关系.
.同学们以“一块直角三角板和一把直尺”开展数学活动,提出了很多数学问题,请你解答:
(1)如图1,∠α和∠β具有怎样的数量关系?请说明理由;
(2)如图2,∠DFC的平分线与∠EGC的平分线相交于点Q,求∠FQG的大小.
.探究题
(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,当∠A+∠B=70°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=∠BCD∠ADE,当∠A+∠B=n°时 .
一.选择题
.如图,AF是∠BAC的平分线,DF∥AC,则∠BAF的度数为( )
A.17.5° B.35° C.55° D.70°
.已知,如图,△ABC中,∠ACB=84°,点D、E分别在BA、BC延长线上,CP平分∠ACE,连接AP( )
A.45° B.48° C.60° D.66°
.如图,在△ABC中,AD是高,若AD=3,S△ABC=12,则BE的长为( )
A.1 B. C.2 D.4
.一个多边形的内角和为720°,则从这多边形的一个顶点最多可以引出几条对角线?( )
A.3条 B.4条 C.5条 D.2条
.如图,在四边形ABCD中,∠A=45°.直线EF分别与边AD,F,则∠1+∠2的度数为( )
A.245° B.225° C.145° D.135°
.下列说法正确的是( )
A.若AC=BC,则点C是线段AB的中点
B.30.15°=30°15′
C.若经过某个多边形一个顶点的所有对角线,将这个多边形分成八个三角形,则这个多形是九边形
D.钟表上的时间是11点10分,此时时针与分针所成的夹角是85°
.王师傅想做一个三角形的框架,他有两根长度分别为8cm和10cm的细木条,需要将其中一根木条分为两段,那么他可以把细木条分为两截的是( )
A.8cm的木条 B.10cm的木条 C.两根都可以 D.两根都不行
.如图,在六边形ABCDEF中,若∠1+∠2=85°( )
A.180° B.245° C.275° D.300°
.已知三角形的三边长分别是4,8,a+1,则a的取值可能是( )
A.10 B.11 C.12 D.13
.如图所示,∠ACB=∠DCE=90°.则下列结论:
①∠1=∠3;
②∠2+∠BCE=180°;
③若AB∥CE,则∠2=∠E;
④若∠2=∠B,则∠4=∠E.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
.如图,在三角形ABE中,点D为BE上一点,连接CD,若∠A=70°,则∠BDC= °.
.如果从多边形的一个顶点出发作它的对角线,能将多边形分成10个三角形,那么这个多边形是 边形.
.正六边形的一个内角是正n边形一个外角的5倍,则n等于 .
.如图,三角形ABC的周长为8cm,D为边AC上一点,则五边形ABCGE的周长为 .
.如图所示的是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=10cm,BE=6cm,则图中阴影部分面积为 .
三.解答题
.如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,你是如何思考的?
.如图,已知∠1+∠2=180°,∠DEF=∠A,
求证:
(1)EF∥AB.
(2)∠ACB=∠DEB.
.(1)问题发现:如图①,直线AB∥CD,连结BE,可以发现∠BEC=∠B+∠C.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∴∠B=∠BEF( ).
∵AB∥DC(已知),EF∥AB,
∴EF∥DC( ).
∴∠C=∠CEF.
∵( )=∠BEF+∠CEF,
∴∠BEC=∠B+∠C.(等量代换).
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C=360°﹣∠BEC.
(3)解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,∠2,∠3,∠5之间的数量关系.
.同学们以“一块直角三角板和一把直尺”开展数学活动,提出了很多数学问题,请你解答:
(1)如图1,∠α和∠β具有怎样的数量关系?请说明理由;
(2)如图2,∠DFC的平分线与∠EGC的平分线相交于点Q,求∠FQG的大小.
.探究题
(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,当∠A+∠B=70°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=∠BCD∠ADE,当∠A+∠B=n°时 .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
