6.1 分类加法计数原理与分步乘法计数原理 课件(共35张PPT)
文档属性
| 名称 | 6.1 分类加法计数原理与分步乘法计数原理 课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
6.1分类加法计数原理与分步乘法计数原理
(第1课时)
人教A版2019必修第三册
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法.但当问题中的数量很大时,列举的方法效率不高.能否设计巧妙的“数法”,以提高效率呢?下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
问题1.
春节放假,小兰计划回家过年和家人团聚,从北京回长沙当天有7趟航班和9列火车。
问题1:小兰从北京回长沙的方案有几类?
问题2:这几类方案中各有几种方法?
问题3:小兰从北京到长沙共有多少种不同的方法
两类,即飞机和火车
第1类乘飞机方案:7种方法,第2类坐火车方案:9种方法
共有7+9=16(种)不同方法
问题2. 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36种不同的号码.
问题3.你能说说这个问题的特征吗?
上述计数过程的基本环节是:
(1)确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2)分别计算各类号码的个数;
(3)各类号码的个数相加,得出所有号码的个数.
一般地,有如下分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n 种不同的方法,那么完成这件事共有 种不同的方法
N=m+n
分类加法计数流程
注意:两类不同方案中的方案不相同。
问题4.从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有 4 班, 汽车有2班,轮船有3班.那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以从甲地到乙地共有4 + 2 + 3 = 9种方法。
如果完成一件事有n类不同方案, 在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,那么完成这件事的方法总数为:
N=m1+m2+…+mn
分类加法计数原理推广
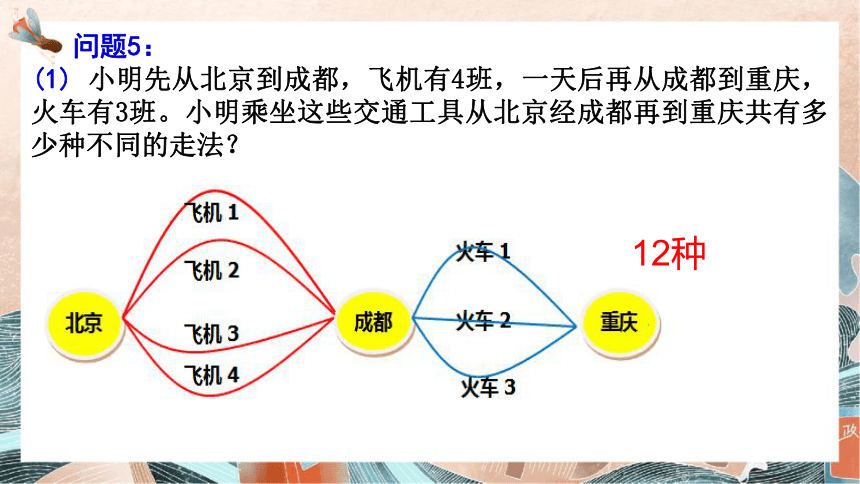
问题5:
(1) 小明先从北京到成都,飞机有4班,一天后再从成都到重庆,火车有3班。小明乘坐这些交通工具从北京经成都再到重庆共有多少种不同的走法?
12种
(2)用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的一个座位编号,总共能够编出多少种不同的号码?
解:解决计数问题可以用“树状图”列举出来
6×9=54种
问题6.你能说说这个问题的特征吗?
上述计数过程的基本环节是:
(1)由问题条件中的“和”,可确定完成编号要分两步;
(2)分别计算各步号码的个数;
(3)将各步号码的个数相乘,得出所有号码的个数.
一般地,有如下分步乘法计数原理:
完成一件事需要分成两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有 种不同的方法
分步乘法计数流程
N= m×n
例2.设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
分析:选出一组参赛代表,可分两步:第一步, 选男生;第二步,选女生
根据分步计数原理,共有 30×24=720种不同方法.
解:第一步,从30名男生中选出1人,有30种不同选择;
第二步,从24名女生中选出1人,有24种不同选择;
如果完成一件事有n步不同方案, 在第1步方案中有m1种不同的方法,在第2步方案中有m2种不同的方法,…,在第n步方案中有mn种不同的方法,那么完成这件事的方法总数为:
N=m1×m2×…×mn
分步乘法计数原理推广
例2.设某班有男生30名,女生24名。现要从中选出男、女生各一名代表
班级参加比赛,共有多少种不同的选法?
解:第一步,从30名男生中选出1人,有30种不同选择;
第二步,从24名女生中选出1人,有24种不同选择;
由分步计数原理:
共有 30×24=720种不同方法.
例3.书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育杂志.
(1)从书架上任取1本书,有多少种不同的取法
(2)从书架的第1、 2、 3层各取1本书,有多少种不同取法
(3)从书架上取2本不同学科的书,有多少种不同的取法
解(1)根据分类加法计数原理可得:N=4+3+2=9;
(2)根据分步乘法计数原理可得:N=4 ×3×2=24;
(3)需先分类再分步.
第一类:从一、二层各取一本,有4×3=12种方法;
第二类:从一、三层各取一本,有4×2=8种方法;
第三类:从二、三层各取一本,有3×2=6种方法;
根据两个基本原理,不同的取法总数是
N=4×3+4×2+3×2=26
答: 从书架上取2本不同种的书,有26种不同的取法.
分类加法计数原理 分步乘法计数原理
相同点
不同点
注意点
用来计算完成一件事的方法种数
每类方案中的每一种方法都能独立完成这件事
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
相加
相乘
类类独立
步步相依
不重不漏
缺一不可
分类、
分步、
问题:分类加法计数原理与分步乘法计数原理的相同点和不同点是什么
课堂小结
一般地,有如下分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n 种不同的方法,那么完成这件事共有 种不同的方法
N=m+n
一般地,有如下分步乘法计数原理:
完成一件事需要分成两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有 种不同的方法
N= m×n
加法计数原理:针对的是“分类”问题.各类方法相互独立.
乘法计数原理:针对的是“分步”问题。 每步相互依存。
课堂练习(课本P5)
1. 填空题
(1) 一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________;
(2) 从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是_________.
9
6
2. 在例1中,如果数学也是A大学的强项专业,那么A大学共有6个专业可以选择,B大学共有4个专业可以选择,应用分类加法计数原理,得到这名同学可能的专业选择种数为6+4=10. 这种算法有什么问题?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
数学
解:这种算法有问题,因为问题强调的是这名同学的专业选择,故并不需要考虑学校的差异,所以这名同学可能的专业选择种数应当为
3. 书架上层放有6本不同的数学书,下层放有5本不同的语文书.
(1) 从书架上任取1本书,有多少种不同的取法
(2) 从书架上任取数学书和语文书各1本,有多少种不同的取法
4. 现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名.
(1) 从三个年级的学生中任选1人参加接待外宾的活动,有多少种不同的选法
(2) 从三个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法
解:(1) 11种;(2) 30种.
解:(1) 12种;(2) 60种.
THANKS
“
”
创新设计习题讲解
训练1 (1)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( )
B
A.14 B.13 C.12 D.10
解析 由于a,b∈{-1,0,1,2},
②当a≠0时,Δ=4-4ab≥0,得ab≤1.
若a=-1时,则b=-1,0,1,2,有序数对(-1,b)有4个;
若a=1时,则b=-1,0,1,有序数对(1,b)有3个;
若a=2时,则b=0,-1,有序数对(2,b)有2个,
故由分类加法计数原理知共有(a,b)的个数为4+4+3+2=13.
训练3 某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人到边远地区支教,有多少种不同的选法?
解 由题意,知有1人既会英语又会日语,6人只会英语,2人只会日语.
法一 分两类.
第一类:从只会英语的6人中选1人教英语,有6种选法,则教日语的有2+1=3(种)选法,此时共有6×3=18(种)选法.
第二类:从不只会英语的1人中选1人教英语,有1种选法,则选教日语的有2种选法,此时有1×2=2(种)选法.
所以由分类加法计算原理知,共有18+2=20(种)选法.
法二 设既会英语又会日语的人为甲,则甲有入选、不入选两类情形,入选后又要分两种:(1)教英语;(2)教日语.
第一类:甲入选.
(1)甲教英语,再从只会日语的2人中选1人,由分步乘法计数原理,有1×2=2(种)选法;
(2)甲教日语,再从只会英语的6人中选1人,由分步乘法计数原理,有1×6=6(种)选法.
故甲入选的不同选法共有2+6=8(种).
第二类:甲不入选.可分两步:
第一步,从只会英语的6人中选1人有6种选法;
第二步,从只会日语的2人中选1人有2种选法.
由分步乘法计数原理知,有6×2=12(种)不同的选法.
综上,共有8+12=20(种)不同选法.
创新设计习题讲解
——分层精练
6.1分类加法计数原理与分步乘法计数原理
(第1课时)
人教A版2019必修第三册
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法.但当问题中的数量很大时,列举的方法效率不高.能否设计巧妙的“数法”,以提高效率呢?下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
问题1.
春节放假,小兰计划回家过年和家人团聚,从北京回长沙当天有7趟航班和9列火车。
问题1:小兰从北京回长沙的方案有几类?
问题2:这几类方案中各有几种方法?
问题3:小兰从北京到长沙共有多少种不同的方法
两类,即飞机和火车
第1类乘飞机方案:7种方法,第2类坐火车方案:9种方法
共有7+9=16(种)不同方法
问题2. 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36种不同的号码.
问题3.你能说说这个问题的特征吗?
上述计数过程的基本环节是:
(1)确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2)分别计算各类号码的个数;
(3)各类号码的个数相加,得出所有号码的个数.
一般地,有如下分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n 种不同的方法,那么完成这件事共有 种不同的方法
N=m+n
分类加法计数流程
注意:两类不同方案中的方案不相同。
问题4.从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有 4 班, 汽车有2班,轮船有3班.那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以从甲地到乙地共有4 + 2 + 3 = 9种方法。
如果完成一件事有n类不同方案, 在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,那么完成这件事的方法总数为:
N=m1+m2+…+mn
分类加法计数原理推广
问题5:
(1) 小明先从北京到成都,飞机有4班,一天后再从成都到重庆,火车有3班。小明乘坐这些交通工具从北京经成都再到重庆共有多少种不同的走法?
12种
(2)用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的一个座位编号,总共能够编出多少种不同的号码?
解:解决计数问题可以用“树状图”列举出来
6×9=54种
问题6.你能说说这个问题的特征吗?
上述计数过程的基本环节是:
(1)由问题条件中的“和”,可确定完成编号要分两步;
(2)分别计算各步号码的个数;
(3)将各步号码的个数相乘,得出所有号码的个数.
一般地,有如下分步乘法计数原理:
完成一件事需要分成两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有 种不同的方法
分步乘法计数流程
N= m×n
例2.设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
分析:选出一组参赛代表,可分两步:第一步, 选男生;第二步,选女生
根据分步计数原理,共有 30×24=720种不同方法.
解:第一步,从30名男生中选出1人,有30种不同选择;
第二步,从24名女生中选出1人,有24种不同选择;
如果完成一件事有n步不同方案, 在第1步方案中有m1种不同的方法,在第2步方案中有m2种不同的方法,…,在第n步方案中有mn种不同的方法,那么完成这件事的方法总数为:
N=m1×m2×…×mn
分步乘法计数原理推广
例2.设某班有男生30名,女生24名。现要从中选出男、女生各一名代表
班级参加比赛,共有多少种不同的选法?
解:第一步,从30名男生中选出1人,有30种不同选择;
第二步,从24名女生中选出1人,有24种不同选择;
由分步计数原理:
共有 30×24=720种不同方法.
例3.书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育杂志.
(1)从书架上任取1本书,有多少种不同的取法
(2)从书架的第1、 2、 3层各取1本书,有多少种不同取法
(3)从书架上取2本不同学科的书,有多少种不同的取法
解(1)根据分类加法计数原理可得:N=4+3+2=9;
(2)根据分步乘法计数原理可得:N=4 ×3×2=24;
(3)需先分类再分步.
第一类:从一、二层各取一本,有4×3=12种方法;
第二类:从一、三层各取一本,有4×2=8种方法;
第三类:从二、三层各取一本,有3×2=6种方法;
根据两个基本原理,不同的取法总数是
N=4×3+4×2+3×2=26
答: 从书架上取2本不同种的书,有26种不同的取法.
分类加法计数原理 分步乘法计数原理
相同点
不同点
注意点
用来计算完成一件事的方法种数
每类方案中的每一种方法都能独立完成这件事
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
相加
相乘
类类独立
步步相依
不重不漏
缺一不可
分类、
分步、
问题:分类加法计数原理与分步乘法计数原理的相同点和不同点是什么
课堂小结
一般地,有如下分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n 种不同的方法,那么完成这件事共有 种不同的方法
N=m+n
一般地,有如下分步乘法计数原理:
完成一件事需要分成两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,则完成这件事共有 种不同的方法
N= m×n
加法计数原理:针对的是“分类”问题.各类方法相互独立.
乘法计数原理:针对的是“分步”问题。 每步相互依存。
课堂练习(课本P5)
1. 填空题
(1) 一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________;
(2) 从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是_________.
9
6
2. 在例1中,如果数学也是A大学的强项专业,那么A大学共有6个专业可以选择,B大学共有4个专业可以选择,应用分类加法计数原理,得到这名同学可能的专业选择种数为6+4=10. 这种算法有什么问题?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
数学
解:这种算法有问题,因为问题强调的是这名同学的专业选择,故并不需要考虑学校的差异,所以这名同学可能的专业选择种数应当为
3. 书架上层放有6本不同的数学书,下层放有5本不同的语文书.
(1) 从书架上任取1本书,有多少种不同的取法
(2) 从书架上任取数学书和语文书各1本,有多少种不同的取法
4. 现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名.
(1) 从三个年级的学生中任选1人参加接待外宾的活动,有多少种不同的选法
(2) 从三个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法
解:(1) 11种;(2) 30种.
解:(1) 12种;(2) 60种.
THANKS
“
”
创新设计习题讲解
训练1 (1)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( )
B
A.14 B.13 C.12 D.10
解析 由于a,b∈{-1,0,1,2},
②当a≠0时,Δ=4-4ab≥0,得ab≤1.
若a=-1时,则b=-1,0,1,2,有序数对(-1,b)有4个;
若a=1时,则b=-1,0,1,有序数对(1,b)有3个;
若a=2时,则b=0,-1,有序数对(2,b)有2个,
故由分类加法计数原理知共有(a,b)的个数为4+4+3+2=13.
训练3 某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人到边远地区支教,有多少种不同的选法?
解 由题意,知有1人既会英语又会日语,6人只会英语,2人只会日语.
法一 分两类.
第一类:从只会英语的6人中选1人教英语,有6种选法,则教日语的有2+1=3(种)选法,此时共有6×3=18(种)选法.
第二类:从不只会英语的1人中选1人教英语,有1种选法,则选教日语的有2种选法,此时有1×2=2(种)选法.
所以由分类加法计算原理知,共有18+2=20(种)选法.
法二 设既会英语又会日语的人为甲,则甲有入选、不入选两类情形,入选后又要分两种:(1)教英语;(2)教日语.
第一类:甲入选.
(1)甲教英语,再从只会日语的2人中选1人,由分步乘法计数原理,有1×2=2(种)选法;
(2)甲教日语,再从只会英语的6人中选1人,由分步乘法计数原理,有1×6=6(种)选法.
故甲入选的不同选法共有2+6=8(种).
第二类:甲不入选.可分两步:
第一步,从只会英语的6人中选1人有6种选法;
第二步,从只会日语的2人中选1人有2种选法.
由分步乘法计数原理知,有6×2=12(种)不同的选法.
综上,共有8+12=20(种)不同选法.
创新设计习题讲解
——分层精练
