沪科版数学九年级上册第22章 相似性 学情评估(含答案)
文档属性
| 名称 | 沪科版数学九年级上册第22章 相似性 学情评估(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 09:16:27 | ||
图片预览




文档简介
第22章学情评估
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
2.下列四组线段中,成比例的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,d=18
C.a=1,b=3,c=2,d=8 D.a=1,b=2,c=4,d=6
3.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
INCLUDEPICTURE"卷+21.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+21.tif" \* MERGEFORMATINET (第3题) INCLUDEPICTURE"J13.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J13.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"卷+23.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+23.tif" \* MERGEFORMATINET (第6题)
4.已知线段AB=2,点P是线段AB的黄金分割点(AP>BP),则线段AP的长为( )
A.+1 B.-1 C. D.
5.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B.=
C.∠ACD=∠B D.AC2=AD·AB
6.如图,在△ABC中,AB∥DE,若=,则△ECD与△ACB的面积之比为( )
A. B. C. D.
7.如图,小明在A时测得某树的影长为3 m,B时又测得该树的影长为2 m,若两次日照的光线互相垂直,则树的高度为( )
A.±m B.m C.6 m D. m
INCLUDEPICTURE"J14.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J14.tif" \* MERGEFORMATINET (第7题) INCLUDEPICTURE"J16.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J16.tif" \* MERGEFORMATINET (第9题) INCLUDEPICTURE"卷+27.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+27.tif" \* MERGEFORMATINET (第10题)
8.若一个三角形能够分成两个与原三角形都相似的三角形,就把这样的三角形称为和谐三角形,则下列选项中属于和谐三角形的是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰三角形或直角三角形
9.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC, E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交对角线AC于点H,连接BH.下列结论错误的是( )
A.HE=2BE B.AC⊥DE
C.∠CED=60° D.S△ADE= 2S△BCE
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是________.
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA′B′C′与矩形OABC位似,位似中心是原点O,且矩形OA′B′C′的面积等于矩形OABC面积的,则点B′的坐标是________________.
INCLUDEPICTURE"卷+28.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+28.tif" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"J17.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J17.tif" \* MERGEFORMATINET (第13题)
13.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为______.
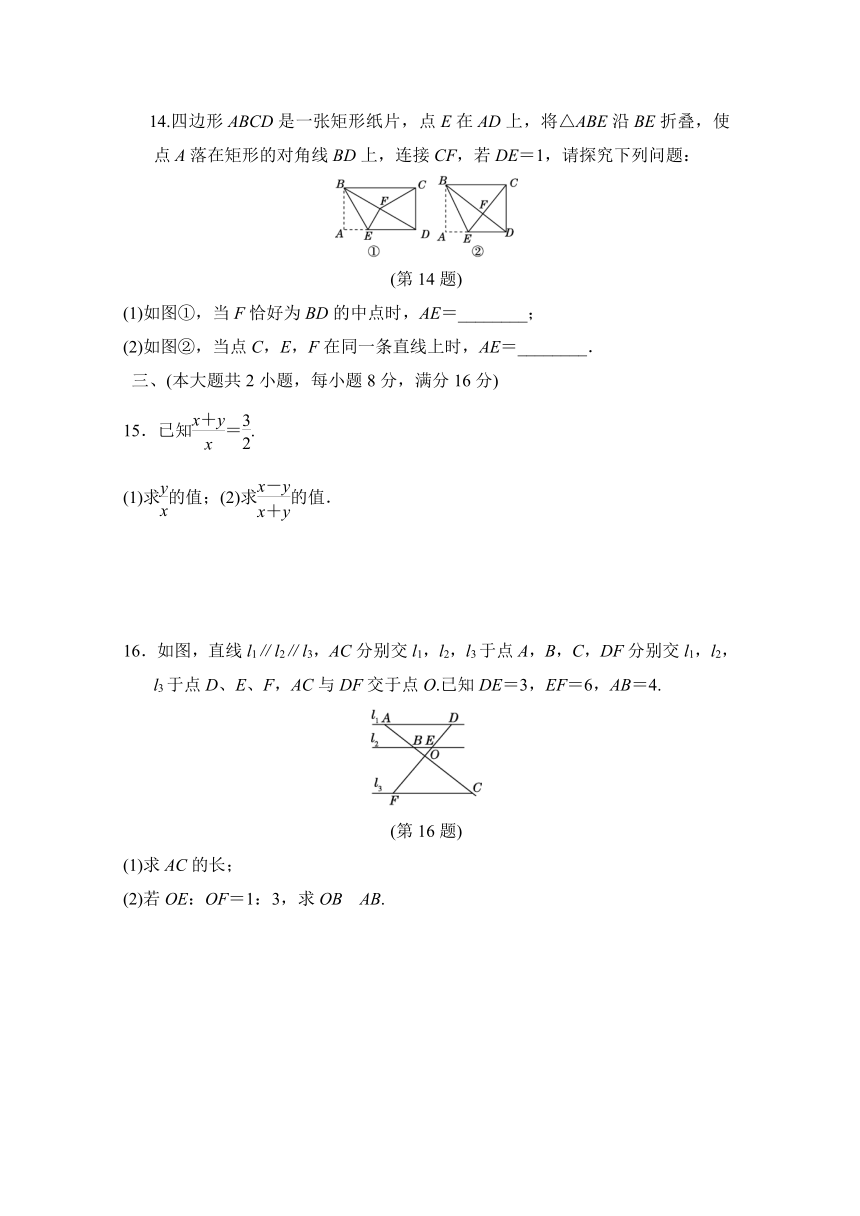
14.四边形ABCD是一张矩形纸片,点E在AD上,将△ABE沿BE折叠,使点A落在矩形的对角线BD上,连接CF,若DE=1,请探究下列问题:
INCLUDEPICTURE"J18.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J18.tif" \* MERGEFORMATINET
(第14题)
(1)如图①,当F恰好为BD的中点时,AE=________;
(2)如图②,当点C,E,F在同一条直线上时,AE=________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知=.
(1)求的值;(2)求的值.
16.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C,DF分别交l1,l2,l3于点D、E、F,AC与DF交于点O.已知DE=3,EF=6,AB=4.
INCLUDEPICTURE"J19.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J19.tif" \* MERGEFORMATINET
(第16题)
(1)求AC的长;
(2)若OE:OF=1:3,求OB?AB.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,每个小正方形的边长都是1个单位,△ABC的顶点都在格点上.
INCLUDEPICTURE"卷+32.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+32.tif" \* MERGEFORMATINET
(第17题)
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)已知△ABC的面积为,则△A1B1C1的面积为______.
18.如图,在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线.求证:AD2=AC·DC.
INCLUDEPICTURE"J20.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J20.tif" \* MERGEFORMATINET (第18题)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求CE的长.
INCLUDEPICTURE"卷+35.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+35.tif" \* MERGEFORMATINET
(第19题)
20.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6 ,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
INCLUDEPICTURE"卷+34.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+34.tif" \* MERGEFORMATINET
(第20题)
六、(本题满分12分)
21.如图,在△ABC中,点D,E分别在边BC,AC上,连接AD,DE,且∠B=∠ADE=∠C.
(1)求证:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动(点D不与B,C重合),且当△ADE是等腰三角形时,求BD的长.
INCLUDEPICTURE"卷+36.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+36.tif" \* MERGEFORMATINET
(第21题)
七、(本题满分12分)
22.如图为幸福小区入口处安装的汽车出入道闸示意图,如图①,道闸关闭时,四边形ABCD是矩形,如图②,在道闸打开的过程中,边AD固定,AD⊥直线l,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行,P为CD上的一点(不与点C,D重台),过点P作PE⊥直线l,PF⊥MN,垂足分别为E,F,即四边形PENF是矩形,过点D作DQ⊥PE,垂足为Q,延长BC与PF相交于点R.
(1)△PDQ与△CPR相似吗?请判断并说明理由;
(2)如图②,若道闸长AB=4米,宽AD=1米,点D距地面0.2米,PE=1.16米,RF=0.8米,CR=1.44米.
①求点B到地面l的距离;
②直接写出PF的长.
INCLUDEPICTURE"J21.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J21.tif" \* MERGEFORMATINET
(第22题)
八、(本题满分14分)
23.在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,F,E是AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
(1)求证:∠FDC=∠AEB;
(2)如图①,若AE=3CE=6,求BG的长;
(3)如图②,若F为AC上任意一点,连接AG,求证:∠EAG=∠ABE.
INCLUDEPICTURE"J22.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J22.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.B 3.B 4.B 5.B 6.B 7.B 8.C 9.A
10.A 【点拨】∵△DAB∽△DCA,
∴=,∴=.
解得BD=4(负值舍去).
∴===,∴AC=AB.
∵AC2=AB(AB+BC),
∴=AB(AB+BC),
解得AB=4,AB=0(舍去),
∴AB=BD=4.
过点B作BH⊥AD于点H.∴AH=AD=3,
∴BH==.
∵AD=3AP,AD=6,∴AP=2.
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,∴=,∴PQ=.
二、11.4?3
12.(3,2)或(-3,-2)
13.或 【点拨】∵将△BDE沿DE翻折得到△FDE,
∴BE=FE.∵BC=8,∴CE=8-BE.
当△CEF与△ABC相似时,=或=,
即=或=,解得BE=或.
14.(1) (2) 【点拨】(1)当F恰好为BD的中点时,由折叠的性质得EF⊥BD,∴EB=ED=1,∴∠EBD=∠EDB.
由折叠的性质得∠ABE=∠EBD.
∴∠ABE=∠EBD=∠ADB.
又∵∠ABE+∠DBE+∠ADB=90°,
∴∠ABE=∠DBE=∠ADB=30°,
∴AE=BE=×1=.
(2)当点C,E,F在同一直线上时,根据折叠的性质可知
BF=BA=CD,∠A=∠BFC=∠CDE=90°.
∵BC∥AD,∴∠BCF=∠CED,
∴△BFC≌△CDE,∴FC=DE=1.
设AE=x,可得EF=x.
∵∠DEF=∠CED,∠EFD=∠EDC,
∴△DEF∽△CED,
∴=,
∴DE2=EF·EC,∴12=x(x+1),
解得x1=,x2=(舍去负值),∴AE=.
三、15.解:∵=,∴x=2y.
(1)==.
(2)==.
16.解:(1)∵l1∥l2∥l3,
∴DE:DF=AB:AC,即3:(3+6)=4:AC,
解得AC=12.
(2)∵l2∥l3,∴△OBE∽△OCF,
∴BE:CF=OB:OC=OE:OF=1:3,∴OC=3OB.
∵AB=4,AC=12,∴BC=8,即OC+OB=8,
∴4OB=8,∴OB=2,∴OB:AB=2:4=1:2.
四、17.解:(1)略 (2)14
18.证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°.
∵BD为∠ABC的平分线,∴∠ABD=∠DBC=36°,
∴∠ABD=∠A,∠BDC=∠A+∠ABD=72°,
∴BD=AD,∠C=∠BDC,
∴∠ABC=∠BDC,BC=BD=AD,
∴△BCD∽△ACB.
∴=,∴=,
∴AD2=AC·DC.
五、19.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,∴∠BAF+∠AFB=90°.
由折叠易得∠AFE=90°,∴∠EFC+∠AFB=90°,
∴∠BAF=∠CFE,∴△ABF∽△FCE.
(2)解:在矩形ABCD中,易得BC=AD=AF=4.
在Rt△ABF中,BF==2,
∴CF=BC-BF=2.
∵△ABF∽△FCE,∴=,即=.
解得CE=.
20.(1)解:∵∠ACB=90°,AB=6 ,BC=6,
∴AC==12.∴AE=AC-CE=9.
∵AB∥CD,∴△CDE∽△ABE.∴=,
∴CD===2 .
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3 .∵△CDE∽△ABE,
∴==,∴DE=,∴BD=4 .
∵==,∠D=∠D,∴△CDE∽△BDC.
六、21.(1)证明:∵∠B=∠ADE=∠C,
∴∠BAD=180°-∠ADB-∠B=180°-∠ADB-∠ADE.
∵∠CDE=180°-∠ADB-∠ADE,
∴∠BAD=∠CDE,∴△BDA∽△CED.
(2)解:由题易知∠BAC=90°.
当AD=AE时,∠ADE=∠AED.
∵∠ADE=∠B=45°,∴∠AED=45°.∴∠DAE=90°.
∴点D与点B重合,不合题意,舍去.
当EA=ED时,∠EAD=∠EDA=∠B=45°.
∵∠BAC=90°,∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,∴AD垂直平分BC,∴BD=3.
当DA=DE时,∵∠EDA=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:CA=DE:CD,∴AC=DC.
∵∠BAC=90°,∠B=45°,BC=6,
∴AC=3 .∴DC=3 .∴BD=BC-DC=6-3 .
综上所述,当△ADE是等腰三角形时,BD的长为3或 6-3 .
七、22.解:(1)相似.
理由:∵四边形PENF是矩形,∴PF∥l,PE∥MN.
∵DQ⊥PQ,∴DQ∥PF,∴∠CPR=∠PDQ.
∵AD⊥l,AD∥BC,PF∥l,∴BR⊥PF,
∴∠CRP=∠PQD=90°,∴△PDQ∽△CPR.
(2)①延长CR交直线l于点G,则点B到地面l的距离即为线段BC+CR+RG的长,如图.
∵四边形PENF是矩形,∴PE⊥l,PF∥l,PE⊥PF.
∵AD∥BC,AD⊥l,∴BC⊥l,∴BG⊥l,
∴四边形PEGR是矩形,∴RG=PE.∵PE=1.16米,
CR=1.44米,BC=AD=1米,
∴BG=BC+CR+RG=BC+CR+PE=1+1.44+1.16=3.6(米).
故点B到地面l的距离为3.6米.
②PF的长为2.72米. 【点拨】∵道闸长AB=4米,设PC=x米,则DP=(4-x)米,由(1)知△PDQ∽△CPR,∴=.
∵点D距地面0.2米,PE=1.16米,CR=1.44米,
∴PQ=PE-QE=1.16-0.2=0.96(米),
∴=,解得x=2.4,
在Rt△CPR中,CR=1.44米,PC=2.4米,
∴PR===1.92(米).
PF=1.92+0.8=2.72(米).故PF的长为2.72米.
INCLUDEPICTURE"D-49.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET (第22题)
八、23.(1)证明:∵∠BAC=90°,AB=AC,
∴∠C=45°.
∵∠BGD=∠EGF=45°,∴∠C=∠BGD.
∵∠FDC=∠EBC+∠BGD,∠AEB=∠EBC+∠C,
∴∠FDC=∠AEB.
(2)解:∵AE=3CE=6,
∴CE=2,∴AB=AC=8.
∵∠A=90°,
∴BE==10,BC==8 .
∵D是BC的中点,∴BD=4 .
∵∠C=∠EGF=∠BGD=45°,∠DBG=∠EBC,
∴△BGD∽△BCE,
∴=,即=,∴BG=.
(3)证明:连接AD.
∵AB=AC,D为BC的中点,∴AD⊥BC,
∴∠ADB=∠BAC=90°.
∵∠ABD=∠ABC,∴△ABD∽△CBA,
∴=,∴AB2=BD·BC.
由(2)知△BGD∽△BCE,∴=.
∴BD·BC=BG·BE,∴AB2=BG·BE,∴=.
∵∠ABG=∠EBA,∴△ABG∽△EBA,
∴∠AGB=∠BAE=90°,
∴∠EAG+∠BAG=∠BAG+∠ABE=90°,
∴∠EAG=∠ABE.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
2.下列四组线段中,成比例的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,d=18
C.a=1,b=3,c=2,d=8 D.a=1,b=2,c=4,d=6
3.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
INCLUDEPICTURE"卷+21.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+21.tif" \* MERGEFORMATINET (第3题) INCLUDEPICTURE"J13.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J13.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"卷+23.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+23.tif" \* MERGEFORMATINET (第6题)
4.已知线段AB=2,点P是线段AB的黄金分割点(AP>BP),则线段AP的长为( )
A.+1 B.-1 C. D.
5.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B.=
C.∠ACD=∠B D.AC2=AD·AB
6.如图,在△ABC中,AB∥DE,若=,则△ECD与△ACB的面积之比为( )
A. B. C. D.
7.如图,小明在A时测得某树的影长为3 m,B时又测得该树的影长为2 m,若两次日照的光线互相垂直,则树的高度为( )
A.±m B.m C.6 m D. m
INCLUDEPICTURE"J14.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J14.tif" \* MERGEFORMATINET (第7题) INCLUDEPICTURE"J16.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J16.tif" \* MERGEFORMATINET (第9题) INCLUDEPICTURE"卷+27.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+27.tif" \* MERGEFORMATINET (第10题)
8.若一个三角形能够分成两个与原三角形都相似的三角形,就把这样的三角形称为和谐三角形,则下列选项中属于和谐三角形的是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰三角形或直角三角形
9.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC, E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交对角线AC于点H,连接BH.下列结论错误的是( )
A.HE=2BE B.AC⊥DE
C.∠CED=60° D.S△ADE= 2S△BCE
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是________.
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA′B′C′与矩形OABC位似,位似中心是原点O,且矩形OA′B′C′的面积等于矩形OABC面积的,则点B′的坐标是________________.
INCLUDEPICTURE"卷+28.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+28.tif" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"J17.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J17.tif" \* MERGEFORMATINET (第13题)
13.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为______.
14.四边形ABCD是一张矩形纸片,点E在AD上,将△ABE沿BE折叠,使点A落在矩形的对角线BD上,连接CF,若DE=1,请探究下列问题:
INCLUDEPICTURE"J18.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J18.tif" \* MERGEFORMATINET
(第14题)
(1)如图①,当F恰好为BD的中点时,AE=________;
(2)如图②,当点C,E,F在同一条直线上时,AE=________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知=.
(1)求的值;(2)求的值.
16.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C,DF分别交l1,l2,l3于点D、E、F,AC与DF交于点O.已知DE=3,EF=6,AB=4.
INCLUDEPICTURE"J19.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J19.tif" \* MERGEFORMATINET
(第16题)
(1)求AC的长;
(2)若OE:OF=1:3,求OB?AB.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,每个小正方形的边长都是1个单位,△ABC的顶点都在格点上.
INCLUDEPICTURE"卷+32.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+32.tif" \* MERGEFORMATINET
(第17题)
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)已知△ABC的面积为,则△A1B1C1的面积为______.
18.如图,在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线.求证:AD2=AC·DC.
INCLUDEPICTURE"J20.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J20.tif" \* MERGEFORMATINET (第18题)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求CE的长.
INCLUDEPICTURE"卷+35.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+35.tif" \* MERGEFORMATINET
(第19题)
20.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6 ,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
INCLUDEPICTURE"卷+34.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+34.tif" \* MERGEFORMATINET
(第20题)
六、(本题满分12分)
21.如图,在△ABC中,点D,E分别在边BC,AC上,连接AD,DE,且∠B=∠ADE=∠C.
(1)求证:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动(点D不与B,C重合),且当△ADE是等腰三角形时,求BD的长.
INCLUDEPICTURE"卷+36.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\卷+36.tif" \* MERGEFORMATINET
(第21题)
七、(本题满分12分)
22.如图为幸福小区入口处安装的汽车出入道闸示意图,如图①,道闸关闭时,四边形ABCD是矩形,如图②,在道闸打开的过程中,边AD固定,AD⊥直线l,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行,P为CD上的一点(不与点C,D重台),过点P作PE⊥直线l,PF⊥MN,垂足分别为E,F,即四边形PENF是矩形,过点D作DQ⊥PE,垂足为Q,延长BC与PF相交于点R.
(1)△PDQ与△CPR相似吗?请判断并说明理由;
(2)如图②,若道闸长AB=4米,宽AD=1米,点D距地面0.2米,PE=1.16米,RF=0.8米,CR=1.44米.
①求点B到地面l的距离;
②直接写出PF的长.
INCLUDEPICTURE"J21.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J21.tif" \* MERGEFORMATINET
(第22题)
八、(本题满分14分)
23.在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,F,E是AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
(1)求证:∠FDC=∠AEB;
(2)如图①,若AE=3CE=6,求BG的长;
(3)如图②,若F为AC上任意一点,连接AG,求证:∠EAG=∠ABE.
INCLUDEPICTURE"J22.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\J22.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.B 3.B 4.B 5.B 6.B 7.B 8.C 9.A
10.A 【点拨】∵△DAB∽△DCA,
∴=,∴=.
解得BD=4(负值舍去).
∴===,∴AC=AB.
∵AC2=AB(AB+BC),
∴=AB(AB+BC),
解得AB=4,AB=0(舍去),
∴AB=BD=4.
过点B作BH⊥AD于点H.∴AH=AD=3,
∴BH==.
∵AD=3AP,AD=6,∴AP=2.
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,∴=,∴PQ=.
二、11.4?3
12.(3,2)或(-3,-2)
13.或 【点拨】∵将△BDE沿DE翻折得到△FDE,
∴BE=FE.∵BC=8,∴CE=8-BE.
当△CEF与△ABC相似时,=或=,
即=或=,解得BE=或.
14.(1) (2) 【点拨】(1)当F恰好为BD的中点时,由折叠的性质得EF⊥BD,∴EB=ED=1,∴∠EBD=∠EDB.
由折叠的性质得∠ABE=∠EBD.
∴∠ABE=∠EBD=∠ADB.
又∵∠ABE+∠DBE+∠ADB=90°,
∴∠ABE=∠DBE=∠ADB=30°,
∴AE=BE=×1=.
(2)当点C,E,F在同一直线上时,根据折叠的性质可知
BF=BA=CD,∠A=∠BFC=∠CDE=90°.
∵BC∥AD,∴∠BCF=∠CED,
∴△BFC≌△CDE,∴FC=DE=1.
设AE=x,可得EF=x.
∵∠DEF=∠CED,∠EFD=∠EDC,
∴△DEF∽△CED,
∴=,
∴DE2=EF·EC,∴12=x(x+1),
解得x1=,x2=(舍去负值),∴AE=.
三、15.解:∵=,∴x=2y.
(1)==.
(2)==.
16.解:(1)∵l1∥l2∥l3,
∴DE:DF=AB:AC,即3:(3+6)=4:AC,
解得AC=12.
(2)∵l2∥l3,∴△OBE∽△OCF,
∴BE:CF=OB:OC=OE:OF=1:3,∴OC=3OB.
∵AB=4,AC=12,∴BC=8,即OC+OB=8,
∴4OB=8,∴OB=2,∴OB:AB=2:4=1:2.
四、17.解:(1)略 (2)14
18.证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°.
∵BD为∠ABC的平分线,∴∠ABD=∠DBC=36°,
∴∠ABD=∠A,∠BDC=∠A+∠ABD=72°,
∴BD=AD,∠C=∠BDC,
∴∠ABC=∠BDC,BC=BD=AD,
∴△BCD∽△ACB.
∴=,∴=,
∴AD2=AC·DC.
五、19.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,∴∠BAF+∠AFB=90°.
由折叠易得∠AFE=90°,∴∠EFC+∠AFB=90°,
∴∠BAF=∠CFE,∴△ABF∽△FCE.
(2)解:在矩形ABCD中,易得BC=AD=AF=4.
在Rt△ABF中,BF==2,
∴CF=BC-BF=2.
∵△ABF∽△FCE,∴=,即=.
解得CE=.
20.(1)解:∵∠ACB=90°,AB=6 ,BC=6,
∴AC==12.∴AE=AC-CE=9.
∵AB∥CD,∴△CDE∽△ABE.∴=,
∴CD===2 .
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3 .∵△CDE∽△ABE,
∴==,∴DE=,∴BD=4 .
∵==,∠D=∠D,∴△CDE∽△BDC.
六、21.(1)证明:∵∠B=∠ADE=∠C,
∴∠BAD=180°-∠ADB-∠B=180°-∠ADB-∠ADE.
∵∠CDE=180°-∠ADB-∠ADE,
∴∠BAD=∠CDE,∴△BDA∽△CED.
(2)解:由题易知∠BAC=90°.
当AD=AE时,∠ADE=∠AED.
∵∠ADE=∠B=45°,∴∠AED=45°.∴∠DAE=90°.
∴点D与点B重合,不合题意,舍去.
当EA=ED时,∠EAD=∠EDA=∠B=45°.
∵∠BAC=90°,∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,∴AD垂直平分BC,∴BD=3.
当DA=DE时,∵∠EDA=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:CA=DE:CD,∴AC=DC.
∵∠BAC=90°,∠B=45°,BC=6,
∴AC=3 .∴DC=3 .∴BD=BC-DC=6-3 .
综上所述,当△ADE是等腰三角形时,BD的长为3或 6-3 .
七、22.解:(1)相似.
理由:∵四边形PENF是矩形,∴PF∥l,PE∥MN.
∵DQ⊥PQ,∴DQ∥PF,∴∠CPR=∠PDQ.
∵AD⊥l,AD∥BC,PF∥l,∴BR⊥PF,
∴∠CRP=∠PQD=90°,∴△PDQ∽△CPR.
(2)①延长CR交直线l于点G,则点B到地面l的距离即为线段BC+CR+RG的长,如图.
∵四边形PENF是矩形,∴PE⊥l,PF∥l,PE⊥PF.
∵AD∥BC,AD⊥l,∴BC⊥l,∴BG⊥l,
∴四边形PEGR是矩形,∴RG=PE.∵PE=1.16米,
CR=1.44米,BC=AD=1米,
∴BG=BC+CR+RG=BC+CR+PE=1+1.44+1.16=3.6(米).
故点B到地面l的距离为3.6米.
②PF的长为2.72米. 【点拨】∵道闸长AB=4米,设PC=x米,则DP=(4-x)米,由(1)知△PDQ∽△CPR,∴=.
∵点D距地面0.2米,PE=1.16米,CR=1.44米,
∴PQ=PE-QE=1.16-0.2=0.96(米),
∴=,解得x=2.4,
在Rt△CPR中,CR=1.44米,PC=2.4米,
∴PR===1.92(米).
PF=1.92+0.8=2.72(米).故PF的长为2.72米.
INCLUDEPICTURE"D-49.tif" INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HK安徽\\D-49.tif" \* MERGEFORMATINET (第22题)
八、23.(1)证明:∵∠BAC=90°,AB=AC,
∴∠C=45°.
∵∠BGD=∠EGF=45°,∴∠C=∠BGD.
∵∠FDC=∠EBC+∠BGD,∠AEB=∠EBC+∠C,
∴∠FDC=∠AEB.
(2)解:∵AE=3CE=6,
∴CE=2,∴AB=AC=8.
∵∠A=90°,
∴BE==10,BC==8 .
∵D是BC的中点,∴BD=4 .
∵∠C=∠EGF=∠BGD=45°,∠DBG=∠EBC,
∴△BGD∽△BCE,
∴=,即=,∴BG=.
(3)证明:连接AD.
∵AB=AC,D为BC的中点,∴AD⊥BC,
∴∠ADB=∠BAC=90°.
∵∠ABD=∠ABC,∴△ABD∽△CBA,
∴=,∴AB2=BD·BC.
由(2)知△BGD∽△BCE,∴=.
∴BD·BC=BG·BE,∴AB2=BG·BE,∴=.
∵∠ABG=∠EBA,∴△ABG∽△EBA,
∴∠AGB=∠BAE=90°,
∴∠EAG+∠BAG=∠BAG+∠ABE=90°,
∴∠EAG=∠ABE.
