华师大版数学九年级上册第24章 解直角三角形 学情评估试题(含答案)
文档属性
| 名称 | 华师大版数学九年级上册第24章 解直角三角形 学情评估试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 09:20:47 | ||
图片预览



文档简介
第24章 解直角三角形 学情评估
一、选择题(每题3分,共24分)
1.Rt△ABC中,∠C=90°,若∠A=30°,AC=2 ,则BC=( )
A.2 B.2 C.4 D.6
2.如图是某博物馆大厅电梯的截面图,AB的长为12 m,AB与AC的夹角为α,则高BC是( )
A.12sin α m B.12cos α m C. m D. m
INCLUDEPICTURE"J24-1.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-1.tif" \* MERGEFORMATINET (第2题) INCLUDEPICTURE"XD48.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\XD48.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\XD48.tif" \* MERGEFORMATINET (第3题)
INCLUDEPICTURE"M20.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M20.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"M21.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M21.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M21.tif" \* MERGEFORMATINET (第7题)
3.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,D为AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
4.在△ABC中,已知∠C=90°,BC=4,sin A=,那么边AC的长是( )
A.6 B.2 C.3 D.2
5. 如图是我们经常看到的一种折叠桌子的示意图,它是由下面的支架AD,BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
6.关于三角函数有如下的公式:sin(α-β)=sin αcos β-cos αsin β,由该公式可求得sin 15°的值是( )
A. B. C. D.
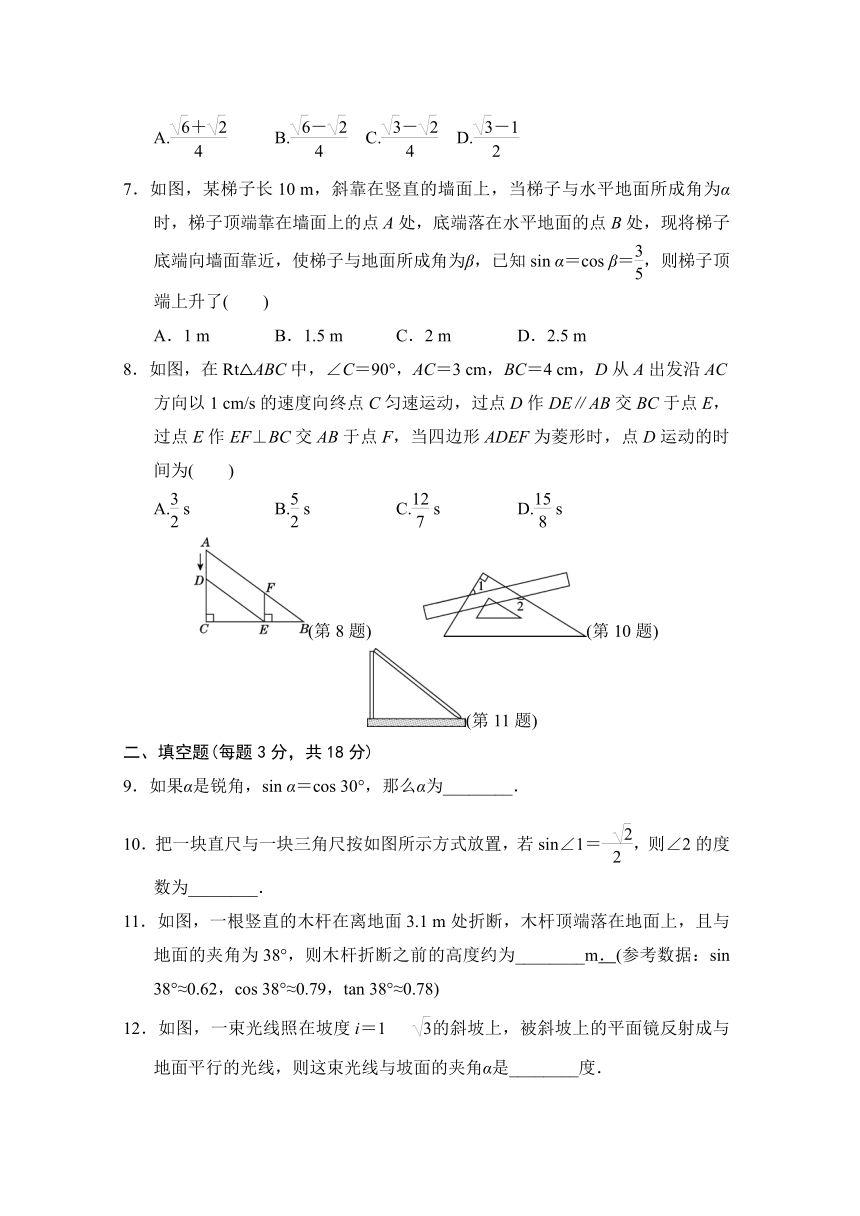
7.如图,某梯子长10 m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sin α=cos β=,则梯子顶端上升了( )
A.1 m B.1.5 m C.2 m D.2.5 m
8.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,D从A出发沿AC方向以1 cm/s的速度向终点C匀速运动,过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
INCLUDEPICTURE"M22.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M22.tif" \* MERGEFORMATINET (第8题) INCLUDEPICTURE"M23.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M23.tif" \* MERGEFORMATINET (第10题)
INCLUDEPICTURE"M24.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M24.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M24.tif" \* MERGEFORMATINET (第11题)
二、填空题(每题3分,共18分)
9.如果α是锐角,sin α=cos 30°,那么α为________.
10.把一块直尺与一块三角尺按如图所示方式放置,若sin∠1=,则∠2的度数为________.
11.如图,一根竖直的木杆在离地面3.1 m处折断,木杆顶端落在地面上,且与地面的夹角为38°,则木杆折断之前的高度约为________m.(参考数据:sin 38°≈0.62,cos 38°≈0.79,tan 38°≈0.78)
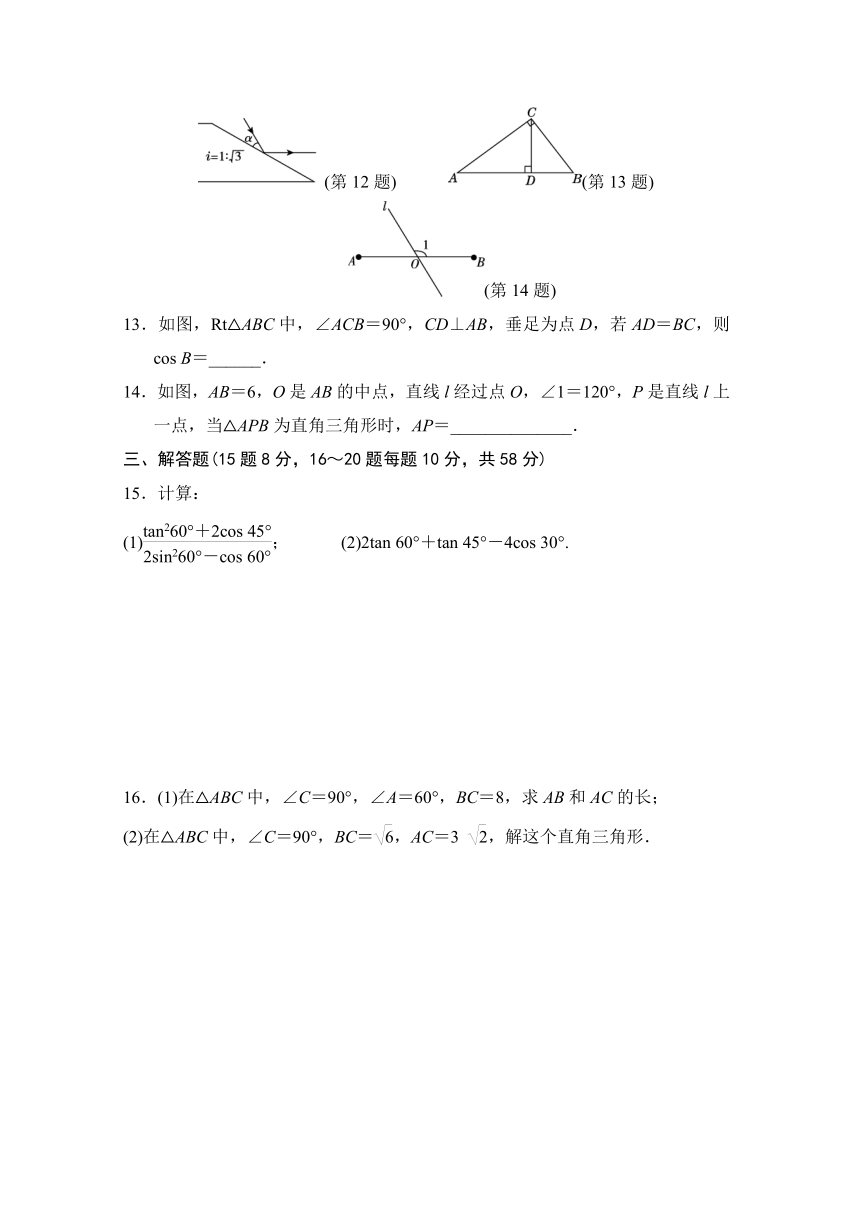
12.如图,一束光线照在坡度i=1? 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
INCLUDEPICTURE"HS30.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\HS30.tif" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"M25.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M25.tif" \* MERGEFORMATINET (第13题)
INCLUDEPICTURE"J30.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J30.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J30.tif" \* MERGEFORMATINET (第14题)
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,若AD=BC,则cos B=______.
14.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=______________.
三、解答题(15题8分,16~20题每题10分,共58分)
15.计算:
(1); (2)2tan 60°+tan 45°-4cos 30°.
16.(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,BC=,AC=3 ,解这个直角三角形.
17.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200 m直道竞速赛.如图所示,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200 m,求点P到赛道AB的距离.(结果保留整数,参考数据:≈1.732)
INCLUDEPICTURE"J24-3.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-3.tif" \* MERGEFORMATINET
(第17题)
18.开封清明上河园是依照北宋画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15 m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5 m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度.(结果精确到1 m,参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
INCLUDEPICTURE"J24-4.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-4.tif" \* MERGEFORMATINET
(第18题)
19. 定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
20.学习了三角函数之后,我们知道,在直角三角形中,知道了一个直角三角形的两条边的长或知道直角三角形的一条边的长及其一个锐角的度数,我们可以求出这个直角三角形其他边的长度和其他角的度数;由“边角边”可知,如果一个三角形的两条边的长度及其这两条边的夹角的度数知道了,那么这个三角形的第三条边一定可以求出来.
应用以上材料,完成下列问题:
(1)如图,在△ABC中,AC=4,BC=6,∠C=60°,求AB的长;
(2)在(1)题图中,如果AC=b,BC=a,∠C=α,你能用a,b和cos α表示AB的长度吗?如果能,写出推导过程;如果不能,说明理由.
INCLUDEPICTURE"J24-5.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-5.tif" \* MERGEFORMATINET
(第20题)
答案
一、1.B 2.A 3.C 4.B 5.D 6.B 7.C 8.D
二、9.60° 10.135° 11.8.1 12.30
13. 点拨:设AD=BC=x,∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,∴∠A=∠BCD.又∵∠B=∠B,∴△ABC ∽△CBD,∴=,即=,∴BD=x(负根舍去),∴cos B==.
14.3或3 或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵O是AB的中点,∠APB=90°,
∴PO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵O是AB的中点,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin 60°=6×=3 .当∠BAP=90°时,如图③,∵O是AB的中点,∴OA=AB=3.∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3 .当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°.∵O是AB的中点,∴OB=AB=3,∴PB=OB·tan∠BOP=3×=3 ,
∴PA==3 .故AP为3或3 或3 .
INCLUDEPICTURE"DA24-2.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-2.tif" \* MERGEFORMATINET (第14题)
三、15.解:(1)原式===3+.
(2)原式=2×+1-4×=2 +1-2 =1.
16.解:(1)在△ABC中,∠C=90°,∠A=60°,BC=8,
∴AB===,
∴AC=AB·cos 60°=×=.
(2)在△ABC中,∠C=90°,BC=,AC=3 ,
∴tan A===,∴∠A=30°,
∴AB=2BC=2 ,∠B=90°-∠A=60°.
17.解:过点P作PC⊥AB,垂足为C.
设PC=x m,在Rt△APC中,∠APC=30°,
∴AC=PC·tan 30°=x(m).在Rt△CBP中,
∠CPB=60°,∴BC=CP·tan 60°=x(m).
∵AB=200 m,∴AC+BC=200 m,∴x+x=200,
∴x=50 ,∴PC=50 m≈87 m,
∴点P到赛道AB的距离约为87 m.
18.解:延长EF交DC于点H.由题意得,∠DHF=90°,
EF=AB=15 m,CH=BF=AE=1.5 m,设FH=x m,
∴EH=EF+FH=(15+x) m.
在Rt△DFH中,∠DFH=45°,
∴DH=FH·tan 45°=x(m).
在Rt△DHE中,∠DEH=34°,
∴tan 34°==≈0.67,∴x≈30.45,
∴DC=DH+CH≈30.45+1.5≈32(m),
∴拂云阁DC的高度约为32 m.
19.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.
作BH⊥AC,垂足为H.在Rt△BHC中,sin C==,
即BC=2BH.
在Rt△BHA中,sin A==,即AB=BH.
∴thi A==.
(2)60°或120°
INCLUDEPICTURE"DA24-6.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-6.tif" \* MERGEFORMATINET
(第19题)
(3)如图,在△ABC中,
∠C=30°,thi A=.
在Rt△BHA中,sin A=.
在Rt△BHC中,sin C==,即BC=2BH.
∴thi A=,即thi A=2sin A.
20.解:(1)过点A作AD⊥BC于点D.
在Rt△ACD中,∵∠ADC=90°,AC=4,∠C=60°,
∴CD=AC·cos C=4×=2,
∴AD2=AC2-CD2=42-22=12.
∵BC=6,CD=2,∴BD=BC-CD=4.
在Rt△ABD中,∵∠ADB=90°,
∴AB===2 .
(2)能.推导过程如下:
过点A作AD⊥BC于点D.在Rt△ACD中,∵∠ADC=90°,AC=b,∠C=α,∴CD=AC·cos C=bcos α,
∴AD2=AC2-CD2=b2-b2cos2α.
∵BC=a,CD=bcos α,∴BD=BC-CD=a-bcos α,
∴在Rt△ABD中,∵∠ADB=90°,
∴AB==
=.
一、选择题(每题3分,共24分)
1.Rt△ABC中,∠C=90°,若∠A=30°,AC=2 ,则BC=( )
A.2 B.2 C.4 D.6
2.如图是某博物馆大厅电梯的截面图,AB的长为12 m,AB与AC的夹角为α,则高BC是( )
A.12sin α m B.12cos α m C. m D. m
INCLUDEPICTURE"J24-1.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-1.tif" \* MERGEFORMATINET (第2题) INCLUDEPICTURE"XD48.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\XD48.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\XD48.tif" \* MERGEFORMATINET (第3题)
INCLUDEPICTURE"M20.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M20.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"M21.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M21.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M21.tif" \* MERGEFORMATINET (第7题)
3.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,D为AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
4.在△ABC中,已知∠C=90°,BC=4,sin A=,那么边AC的长是( )
A.6 B.2 C.3 D.2
5. 如图是我们经常看到的一种折叠桌子的示意图,它是由下面的支架AD,BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
6.关于三角函数有如下的公式:sin(α-β)=sin αcos β-cos αsin β,由该公式可求得sin 15°的值是( )
A. B. C. D.
7.如图,某梯子长10 m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sin α=cos β=,则梯子顶端上升了( )
A.1 m B.1.5 m C.2 m D.2.5 m
8.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,D从A出发沿AC方向以1 cm/s的速度向终点C匀速运动,过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
INCLUDEPICTURE"M22.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M22.tif" \* MERGEFORMATINET (第8题) INCLUDEPICTURE"M23.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M23.tif" \* MERGEFORMATINET (第10题)
INCLUDEPICTURE"M24.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M24.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M24.tif" \* MERGEFORMATINET (第11题)
二、填空题(每题3分,共18分)
9.如果α是锐角,sin α=cos 30°,那么α为________.
10.把一块直尺与一块三角尺按如图所示方式放置,若sin∠1=,则∠2的度数为________.
11.如图,一根竖直的木杆在离地面3.1 m处折断,木杆顶端落在地面上,且与地面的夹角为38°,则木杆折断之前的高度约为________m.(参考数据:sin 38°≈0.62,cos 38°≈0.79,tan 38°≈0.78)
12.如图,一束光线照在坡度i=1? 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
INCLUDEPICTURE"HS30.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\HS30.tif" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"M25.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\M25.tif" \* MERGEFORMATINET (第13题)
INCLUDEPICTURE"J30.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J30.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J30.tif" \* MERGEFORMATINET (第14题)
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,若AD=BC,则cos B=______.
14.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=______________.
三、解答题(15题8分,16~20题每题10分,共58分)
15.计算:
(1); (2)2tan 60°+tan 45°-4cos 30°.
16.(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,BC=,AC=3 ,解这个直角三角形.
17.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200 m直道竞速赛.如图所示,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200 m,求点P到赛道AB的距离.(结果保留整数,参考数据:≈1.732)
INCLUDEPICTURE"J24-3.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-3.tif" \* MERGEFORMATINET
(第17题)
18.开封清明上河园是依照北宋画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15 m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5 m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度.(结果精确到1 m,参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
INCLUDEPICTURE"J24-4.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-4.tif" \* MERGEFORMATINET
(第18题)
19. 定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
20.学习了三角函数之后,我们知道,在直角三角形中,知道了一个直角三角形的两条边的长或知道直角三角形的一条边的长及其一个锐角的度数,我们可以求出这个直角三角形其他边的长度和其他角的度数;由“边角边”可知,如果一个三角形的两条边的长度及其这两条边的夹角的度数知道了,那么这个三角形的第三条边一定可以求出来.
应用以上材料,完成下列问题:
(1)如图,在△ABC中,AC=4,BC=6,∠C=60°,求AB的长;
(2)在(1)题图中,如果AC=b,BC=a,∠C=α,你能用a,b和cos α表示AB的长度吗?如果能,写出推导过程;如果不能,说明理由.
INCLUDEPICTURE"J24-5.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\J24-5.tif" \* MERGEFORMATINET
(第20题)
答案
一、1.B 2.A 3.C 4.B 5.D 6.B 7.C 8.D
二、9.60° 10.135° 11.8.1 12.30
13. 点拨:设AD=BC=x,∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,∴∠A=∠BCD.又∵∠B=∠B,∴△ABC ∽△CBD,∴=,即=,∴BD=x(负根舍去),∴cos B==.
14.3或3 或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵O是AB的中点,∠APB=90°,
∴PO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵O是AB的中点,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin 60°=6×=3 .当∠BAP=90°时,如图③,∵O是AB的中点,∴OA=AB=3.∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3 .当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°.∵O是AB的中点,∴OB=AB=3,∴PB=OB·tan∠BOP=3×=3 ,
∴PA==3 .故AP为3或3 或3 .
INCLUDEPICTURE"DA24-2.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-2.tif" \* MERGEFORMATINET (第14题)
三、15.解:(1)原式===3+.
(2)原式=2×+1-4×=2 +1-2 =1.
16.解:(1)在△ABC中,∠C=90°,∠A=60°,BC=8,
∴AB===,
∴AC=AB·cos 60°=×=.
(2)在△ABC中,∠C=90°,BC=,AC=3 ,
∴tan A===,∴∠A=30°,
∴AB=2BC=2 ,∠B=90°-∠A=60°.
17.解:过点P作PC⊥AB,垂足为C.
设PC=x m,在Rt△APC中,∠APC=30°,
∴AC=PC·tan 30°=x(m).在Rt△CBP中,
∠CPB=60°,∴BC=CP·tan 60°=x(m).
∵AB=200 m,∴AC+BC=200 m,∴x+x=200,
∴x=50 ,∴PC=50 m≈87 m,
∴点P到赛道AB的距离约为87 m.
18.解:延长EF交DC于点H.由题意得,∠DHF=90°,
EF=AB=15 m,CH=BF=AE=1.5 m,设FH=x m,
∴EH=EF+FH=(15+x) m.
在Rt△DFH中,∠DFH=45°,
∴DH=FH·tan 45°=x(m).
在Rt△DHE中,∠DEH=34°,
∴tan 34°==≈0.67,∴x≈30.45,
∴DC=DH+CH≈30.45+1.5≈32(m),
∴拂云阁DC的高度约为32 m.
19.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.
作BH⊥AC,垂足为H.在Rt△BHC中,sin C==,
即BC=2BH.
在Rt△BHA中,sin A==,即AB=BH.
∴thi A==.
(2)60°或120°
INCLUDEPICTURE"DA24-6.tif" INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\九数HS全国\\DA24-6.tif" \* MERGEFORMATINET
(第19题)
(3)如图,在△ABC中,
∠C=30°,thi A=.
在Rt△BHA中,sin A=.
在Rt△BHC中,sin C==,即BC=2BH.
∴thi A=,即thi A=2sin A.
20.解:(1)过点A作AD⊥BC于点D.
在Rt△ACD中,∵∠ADC=90°,AC=4,∠C=60°,
∴CD=AC·cos C=4×=2,
∴AD2=AC2-CD2=42-22=12.
∵BC=6,CD=2,∴BD=BC-CD=4.
在Rt△ABD中,∵∠ADB=90°,
∴AB===2 .
(2)能.推导过程如下:
过点A作AD⊥BC于点D.在Rt△ACD中,∵∠ADC=90°,AC=b,∠C=α,∴CD=AC·cos C=bcos α,
∴AD2=AC2-CD2=b2-b2cos2α.
∵BC=a,CD=bcos α,∴BD=BC-CD=a-bcos α,
∴在Rt△ABD中,∵∠ADB=90°,
∴AB==
=.
