【解析版】甘肃省天水一中2014届高三下学期第一次诊断考试数学(理)试题
文档属性
| 名称 | 【解析版】甘肃省天水一中2014届高三下学期第一次诊断考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 327.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-12 07:59:42 | ||
图片预览




文档简介
甘肃省天水市一中2014届高三年级诊断考试
数学(理)试题
命题人:黄国林 审题人: 蔡恒录
第Ⅰ卷(选择题 共60分)
一、选择题:每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若(a、b都是实数,i为虚数单位),则a+b=
A.1 B.-1 C.7 D.-7
【答案】B
【解析】因为,所以,所以。
2.已知命题p:,且a>0,有,命题q:,,则下列判断正确的是
A.p是假命题 B.q是真命题
C.是真命题 D.是真命题
【答案】C
【解析】命题p:,且a>0,有,是真命题;命题q:,,是假命题,所以是真命题。
3. 如图,设D是边长为l的正方形区域,E是D内函数
与所构成(阴影部分)的区域,在D中任取一点,则该
点在E中的概率是
A. B. C. D.
【答案】D
【解析】图中阴影部分的面积为,
所以所投的点落在叶形图内部的概率。
4.设M是边BC上任意一点,N为AM的中点,若,则λ+μ的值为
A. B. C. D.1
【答案】C
【解析】因为M是边BC上任意一点,设,又,所以。
5. 执行如图所示的程序框图,输出的的值为
A. B. C. D.
【答案】A
【解析】第一次循环:,此时满足条件,继续循环;
第二次循环:,此时满足条件,继续循环;
第三次循环:,此时满足条件,继续循环;
第四次循环:,此时不满足条件,结束循环,所以输出的的值为4.
6. 八个一样的小球排成一排,涂上红、白两种颜色,5个涂红色,
3个涂白色.若涂红色的小球恰好有三个连续,则不同涂法共有
A.36种 B.30种 C.24种 D.20种
【答案】C
【解析】先把3个涂红色的小球捆绑,作为一体,再把3个涂白色的小球排起来,
第一步:把捆绑的小球插入3个涂白色的小球中有4种选择;
第二步:把剩下的2个红色小球插入:2个红色小球分开有3种插法,在一起也有3种插法;即:涂法有4(3+3)=24种。
7.已知函数,则使函数有零点的实数的取值范围是
A. B.
C. D.
【答案】B
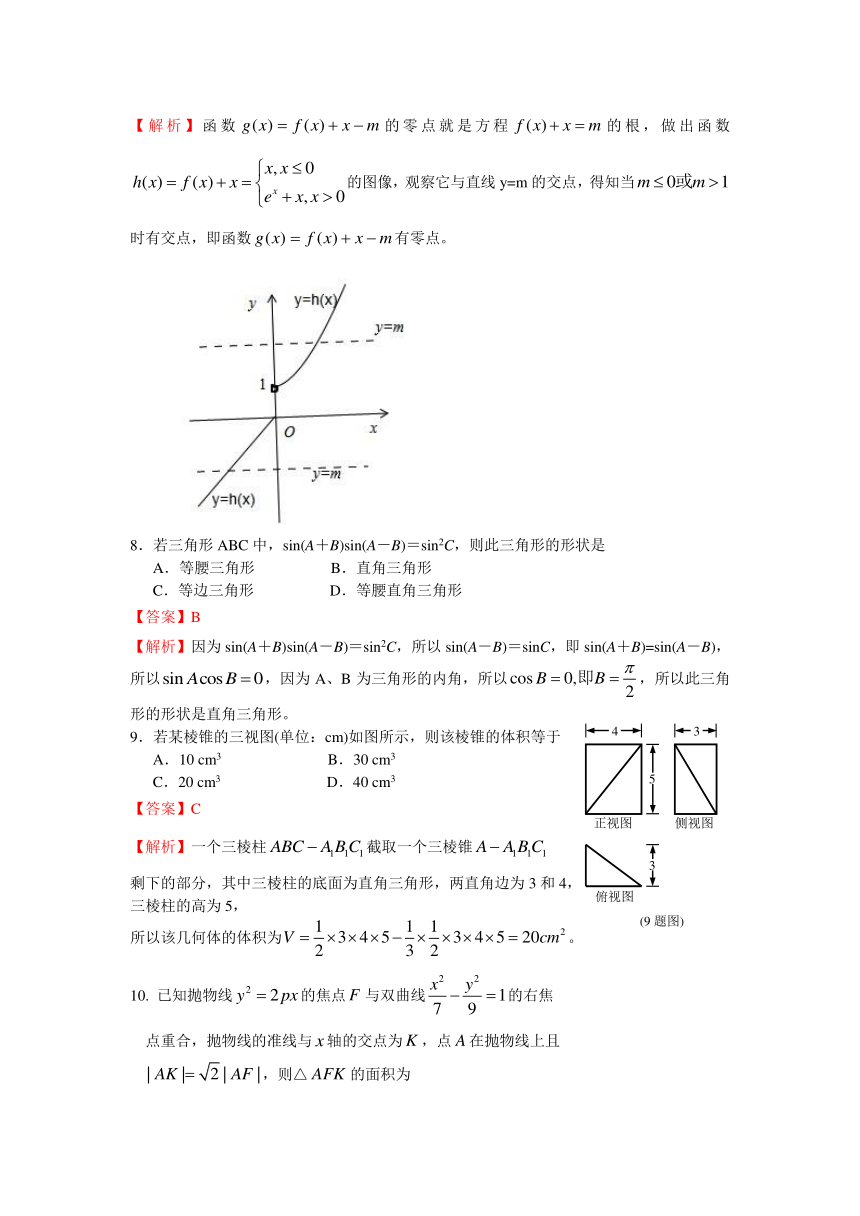
【解析】函数的零点就是方程的根,做出函数的图像,观察它与直线y=m的交点,得知当时有交点,即函数有零点。
8.若三角形ABC中,sin(A+B)sin(A-B)=sin2C,则此三角形的形状是
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
【答案】B
【解析】因为sin(A+B)sin(A-B)=sin2C,所以sin(A-B)=sinC,即sin(A+B)=sin(A-B),所以,因为A、B为三角形的内角,所以,所以此三角形的形状是直角三角形。
9.若某棱锥的三视图(单位:cm)如图所示,则该棱锥的体积等于
A.10 cm3 B.30 cm3
C.20 cm3 D.40 cm3
【答案】C
【解析】一个三棱柱截取一个三棱锥
剩下的部分,其中三棱柱的底面为直角三角形,两直角边为3和4,
三棱柱的高为5,
所以该几何体的体积为。
10. 已知抛物线的焦点与双曲线的右焦
点重合,抛物线的准线与轴的交点为,点在抛物线上且
,则△的面积为
A.4 B.8 C.16 D.32
【答案】D
【解析】因为抛物线的焦点与双曲线的右焦点重合,所以,设A,又,所以,又,解得,所以△的面积为。
11. ,数列的前项和为,数列的通项公式为,则的最小值为
A. B. C. D.
【答案】A
【解析】,所以,所以,所以,当且仅当时等号成立。
12.设函数在(0,+)内有定义,对于给定的正数K,定义函数,取函数,恒有,则
A.K的最大值为 B.K的最小值为
C.K的最大值为2 D.K的最小值为2
【答案】B
【解析】因为,所以,又在(0,+)内单调递减,,所以当时,;当时,。所以在内单调递增,在(1,+)内单调递减,所以函数的最大值的,所以要恒有,则K的最小值为。
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
13. 二项式的展开式中,仅有第5项的二项式系数最大,则其常数项是 ;
【答案】70
【解析】因为仅有第5项的二项式系数最大,所以n=8,所以由得:,由8-2r=0得r=4,所以其常数项是。
14.设x,y满足约束条件,向量,
且a∥b,则m的最小值为 ;
【答案】-6
【解析】因为a∥b,所以,画出约束条件的可行域,由可行域知,目标函数过点(1,8)时取最小值-6.
15.如图,已知球是棱长为的正方体
的内切球,则平面截球的截面面积为 ;
【答案】
【解析】易知球O的圆心为的交点,球的半径为,且球O到面的距离为,所以平面截球的截面圆的半径为,平面截球的截面面积为。
16. 已知f(n)=1+(n∈N*),经计算得
f(4)>2,f(8)>,f(16)>3, f(32)>,……,观察上
述结果,则可归纳出一般结论为 。
【答案】
【解析】观察式子的规律:f(22)>,f()>,f()>, f()>,……,可归纳出一般结论为。
三、解答题:本大题共6道题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分12分)
在△ABC中,分别为内角A, B, C的对边,且
(1)求角A的大小; (2)求的最大值.
18.(本小题满分12分)
某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次,在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知某参赛选手在A区和B区每次投篮进球的概率分别是和.
(Ⅰ)如果以投篮得分的期望值高作为选择的标准,问该选手应该选择哪个区投篮?
请说明理由;
(Ⅱ)求该选手在A区投篮得分高于在B区投篮得分的概率.
19.(本题满分12分)
如图,正方形ADEF与梯形ABCD所在平面互相垂直,
AD⊥CD,AB//CD,AB=AD=,点M在线段
EC上且不与E、C重合。
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值
为时,求三棱锥M—BDE的体积.
20.(本小题满分12分)
已知椭圆经过点,离心率为.
(1)求椭圆C的方程:
(2)过点Q(1,0)的直线l与椭圆C相交于A、B两点,点P(4,3),记直线PA,PB的
斜率分别为k1,k2,当 k1·k2 最大时,求直线l的方程.
21.(本题满分12分)
已知函数
(Ⅰ)求的单调区间;
(Ⅱ)如果当且时,恒成立,求实数的范围.
请考生在题(22)(23)(24)中任选一题作答,如果多做,则按所做的的第一题计分.做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
22.(本题满分10分)选修4—1几何证明选讲:
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,
AC∥DE,AC与BD相交于H点
(Ⅰ)求证:BD平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长
23.(本题满分10分)选修4—4:坐标系与参数方程
在直角坐标系中,以原点为极点,轴的正半轴为极轴建坐标系,已知曲线,已知过点的直线的参数方程为: , 直线与曲线分别交于两点.
(Ⅰ)写出曲线和直线的普通方程;
(Ⅱ)若成等比数列,求的值.
24.(本题满分10分)选修4—5:不等式选讲
(1)解不等式
(2)设 ,试求的最小值及相应的值 。
数学(理)答案
一、选择题:BCDCA CBBCD AB
二、填空题:13. 70 14. -6 15. 16.
三、解答题:本大题共6道题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分12分)
【答案】解:(1)由已知,根据正弦定理得
即, ……………… 3分
由余弦定理得
……………… 6分
(2)由(1)得:
…………9 分
故当时,取得最大值1 . ……………… 12分
18.(本题满分12分)
【答案】解:(Ⅰ)设该选手在A区投篮的进球数为X,则,
则该选手在A区投篮得分的期望为.………………………………………(3分)
设该选手在B区投篮的进球数为Y,则,
则该选手在B区投篮得分的期望为.
所以该选手应该选择A区投篮.………………………………………………………(6分)
(Ⅱ)设“该选手在A区投篮得分高于在B区投篮得分”为事件C,“该选手在A区投篮得4分且在B区投篮得3分或0分”为事件D,“该选手在A区投篮得2分且在B区投篮得0分”为事件E,则事件,且事件D与事件E互斥. …………(7分)
, ………………………………………………………(9分)
, ……………………………………………………………(11分)
,
故该选手在A区投篮得分高于在B区投篮得分的概率为. ……………………(12分)
19.(本小题满分12分)
解:(1)以分别为轴建立空间直角坐标系
则
的一个法向量
,。即 ………………………..4分
(2)依题意设,
设面的法向量
则,
令,则,面的法向量
,解得………………10分
为EC的中点,,到面的距离
…………………………………………………………12分
另解:用传统方法证明相应给分。
20.(本小题满分12分)
试题解析:(1) 由已知可得,所以 ① 1分
又点在椭圆上,所以 ② 2分
由①②解之,得.
故椭圆的方程为. 4分
(2)解法一:①当直线的斜率为0时,则; 5分
②当直线的斜率不为0时,设,,直线的方程为,
将代入,整理得.
则,
又,,
所以,
9分
令,则
当时即时,;
当时,
或
当且仅当,即时, 取得最大值. 11分
由①②得,直线的方程为. 12分
解法二:①当直线垂直于x轴时,则;
②当直线与x轴不垂直时,设,,直线的方程为,
将代入,整理得.
则
又,,
所以,
令由得或
所以当且仅当时最大,所以直线的方程为.
考点:椭圆的几何性质,直线与椭圆的位置关系,直线方程,基本不等式,应用导数研究函数的最值.
21.(本题满分12分)
【答案】(1)定义域为
设
① 当时,对称轴,,所以在上是增函数 -----------------------------2分
② 当时,,所以在上是增函数 ----------------------------------------4分
③ 当时,令得
令解得;令解得
所以的单调递增区间和;的单调递减区间
------------------------------------6分
(2)可化为(※)
设,由(1)知:
① 当时,在上是增函数
若时,;所以
若时,。所以
所以,当时,※式成立--------------------------------------10分
② 当时,在是减函数,所以※式不成立
综上,实数的取值范围是.----------------------------12分
解法二 :可化为
设
令
,
所以
在
由洛必达法则
所以
22.(本题满分10分)选修4—1几何证明选讲:
【答案】(1)
又切圆于点,
而(同弧)
所以,BD平分∠ABC——————————5分
(2)由(1)知,又,
又为公共角,所以与相似。
,因为AB=4,AD=6,BD=8,所以AH=3————————10分
23.(本题满分10分)选修4—4:坐标系与参数方程
【答案】解:(Ⅰ). ……………4分
(Ⅱ)直线的参数方程为(为参数),
代入, 得到, ………7分
则有.
因为,所以. 解得 .…10分
24.(本题满分10分)选修4—5:不等式选讲
数学(理)试题
命题人:黄国林 审题人: 蔡恒录
第Ⅰ卷(选择题 共60分)
一、选择题:每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若(a、b都是实数,i为虚数单位),则a+b=
A.1 B.-1 C.7 D.-7
【答案】B
【解析】因为,所以,所以。
2.已知命题p:,且a>0,有,命题q:,,则下列判断正确的是
A.p是假命题 B.q是真命题
C.是真命题 D.是真命题
【答案】C
【解析】命题p:,且a>0,有,是真命题;命题q:,,是假命题,所以是真命题。
3. 如图,设D是边长为l的正方形区域,E是D内函数
与所构成(阴影部分)的区域,在D中任取一点,则该
点在E中的概率是
A. B. C. D.
【答案】D
【解析】图中阴影部分的面积为,
所以所投的点落在叶形图内部的概率。
4.设M是边BC上任意一点,N为AM的中点,若,则λ+μ的值为
A. B. C. D.1
【答案】C
【解析】因为M是边BC上任意一点,设,又,所以。
5. 执行如图所示的程序框图,输出的的值为
A. B. C. D.
【答案】A
【解析】第一次循环:,此时满足条件,继续循环;
第二次循环:,此时满足条件,继续循环;
第三次循环:,此时满足条件,继续循环;
第四次循环:,此时不满足条件,结束循环,所以输出的的值为4.
6. 八个一样的小球排成一排,涂上红、白两种颜色,5个涂红色,
3个涂白色.若涂红色的小球恰好有三个连续,则不同涂法共有
A.36种 B.30种 C.24种 D.20种
【答案】C
【解析】先把3个涂红色的小球捆绑,作为一体,再把3个涂白色的小球排起来,
第一步:把捆绑的小球插入3个涂白色的小球中有4种选择;
第二步:把剩下的2个红色小球插入:2个红色小球分开有3种插法,在一起也有3种插法;即:涂法有4(3+3)=24种。
7.已知函数,则使函数有零点的实数的取值范围是
A. B.
C. D.
【答案】B
【解析】函数的零点就是方程的根,做出函数的图像,观察它与直线y=m的交点,得知当时有交点,即函数有零点。
8.若三角形ABC中,sin(A+B)sin(A-B)=sin2C,则此三角形的形状是
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
【答案】B
【解析】因为sin(A+B)sin(A-B)=sin2C,所以sin(A-B)=sinC,即sin(A+B)=sin(A-B),所以,因为A、B为三角形的内角,所以,所以此三角形的形状是直角三角形。
9.若某棱锥的三视图(单位:cm)如图所示,则该棱锥的体积等于
A.10 cm3 B.30 cm3
C.20 cm3 D.40 cm3
【答案】C
【解析】一个三棱柱截取一个三棱锥
剩下的部分,其中三棱柱的底面为直角三角形,两直角边为3和4,
三棱柱的高为5,
所以该几何体的体积为。
10. 已知抛物线的焦点与双曲线的右焦
点重合,抛物线的准线与轴的交点为,点在抛物线上且
,则△的面积为
A.4 B.8 C.16 D.32
【答案】D
【解析】因为抛物线的焦点与双曲线的右焦点重合,所以,设A,又,所以,又,解得,所以△的面积为。
11. ,数列的前项和为,数列的通项公式为,则的最小值为
A. B. C. D.
【答案】A
【解析】,所以,所以,所以,当且仅当时等号成立。
12.设函数在(0,+)内有定义,对于给定的正数K,定义函数,取函数,恒有,则
A.K的最大值为 B.K的最小值为
C.K的最大值为2 D.K的最小值为2
【答案】B
【解析】因为,所以,又在(0,+)内单调递减,,所以当时,;当时,。所以在内单调递增,在(1,+)内单调递减,所以函数的最大值的,所以要恒有,则K的最小值为。
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
13. 二项式的展开式中,仅有第5项的二项式系数最大,则其常数项是 ;
【答案】70
【解析】因为仅有第5项的二项式系数最大,所以n=8,所以由得:,由8-2r=0得r=4,所以其常数项是。
14.设x,y满足约束条件,向量,
且a∥b,则m的最小值为 ;
【答案】-6
【解析】因为a∥b,所以,画出约束条件的可行域,由可行域知,目标函数过点(1,8)时取最小值-6.
15.如图,已知球是棱长为的正方体
的内切球,则平面截球的截面面积为 ;
【答案】
【解析】易知球O的圆心为的交点,球的半径为,且球O到面的距离为,所以平面截球的截面圆的半径为,平面截球的截面面积为。
16. 已知f(n)=1+(n∈N*),经计算得
f(4)>2,f(8)>,f(16)>3, f(32)>,……,观察上
述结果,则可归纳出一般结论为 。
【答案】
【解析】观察式子的规律:f(22)>,f()>,f()>, f()>,……,可归纳出一般结论为。
三、解答题:本大题共6道题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分12分)
在△ABC中,分别为内角A, B, C的对边,且
(1)求角A的大小; (2)求的最大值.
18.(本小题满分12分)
某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次,在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知某参赛选手在A区和B区每次投篮进球的概率分别是和.
(Ⅰ)如果以投篮得分的期望值高作为选择的标准,问该选手应该选择哪个区投篮?
请说明理由;
(Ⅱ)求该选手在A区投篮得分高于在B区投篮得分的概率.
19.(本题满分12分)
如图,正方形ADEF与梯形ABCD所在平面互相垂直,
AD⊥CD,AB//CD,AB=AD=,点M在线段
EC上且不与E、C重合。
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值
为时,求三棱锥M—BDE的体积.
20.(本小题满分12分)
已知椭圆经过点,离心率为.
(1)求椭圆C的方程:
(2)过点Q(1,0)的直线l与椭圆C相交于A、B两点,点P(4,3),记直线PA,PB的
斜率分别为k1,k2,当 k1·k2 最大时,求直线l的方程.
21.(本题满分12分)
已知函数
(Ⅰ)求的单调区间;
(Ⅱ)如果当且时,恒成立,求实数的范围.
请考生在题(22)(23)(24)中任选一题作答,如果多做,则按所做的的第一题计分.做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
22.(本题满分10分)选修4—1几何证明选讲:
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,
AC∥DE,AC与BD相交于H点
(Ⅰ)求证:BD平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长
23.(本题满分10分)选修4—4:坐标系与参数方程
在直角坐标系中,以原点为极点,轴的正半轴为极轴建坐标系,已知曲线,已知过点的直线的参数方程为: , 直线与曲线分别交于两点.
(Ⅰ)写出曲线和直线的普通方程;
(Ⅱ)若成等比数列,求的值.
24.(本题满分10分)选修4—5:不等式选讲
(1)解不等式
(2)设 ,试求的最小值及相应的值 。
数学(理)答案
一、选择题:BCDCA CBBCD AB
二、填空题:13. 70 14. -6 15. 16.
三、解答题:本大题共6道题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分12分)
【答案】解:(1)由已知,根据正弦定理得
即, ……………… 3分
由余弦定理得
……………… 6分
(2)由(1)得:
…………9 分
故当时,取得最大值1 . ……………… 12分
18.(本题满分12分)
【答案】解:(Ⅰ)设该选手在A区投篮的进球数为X,则,
则该选手在A区投篮得分的期望为.………………………………………(3分)
设该选手在B区投篮的进球数为Y,则,
则该选手在B区投篮得分的期望为.
所以该选手应该选择A区投篮.………………………………………………………(6分)
(Ⅱ)设“该选手在A区投篮得分高于在B区投篮得分”为事件C,“该选手在A区投篮得4分且在B区投篮得3分或0分”为事件D,“该选手在A区投篮得2分且在B区投篮得0分”为事件E,则事件,且事件D与事件E互斥. …………(7分)
, ………………………………………………………(9分)
, ……………………………………………………………(11分)
,
故该选手在A区投篮得分高于在B区投篮得分的概率为. ……………………(12分)
19.(本小题满分12分)
解:(1)以分别为轴建立空间直角坐标系
则
的一个法向量
,。即 ………………………..4分
(2)依题意设,
设面的法向量
则,
令,则,面的法向量
,解得………………10分
为EC的中点,,到面的距离
…………………………………………………………12分
另解:用传统方法证明相应给分。
20.(本小题满分12分)
试题解析:(1) 由已知可得,所以 ① 1分
又点在椭圆上,所以 ② 2分
由①②解之,得.
故椭圆的方程为. 4分
(2)解法一:①当直线的斜率为0时,则; 5分
②当直线的斜率不为0时,设,,直线的方程为,
将代入,整理得.
则,
又,,
所以,
9分
令,则
当时即时,;
当时,
或
当且仅当,即时, 取得最大值. 11分
由①②得,直线的方程为. 12分
解法二:①当直线垂直于x轴时,则;
②当直线与x轴不垂直时,设,,直线的方程为,
将代入,整理得.
则
又,,
所以,
令由得或
所以当且仅当时最大,所以直线的方程为.
考点:椭圆的几何性质,直线与椭圆的位置关系,直线方程,基本不等式,应用导数研究函数的最值.
21.(本题满分12分)
【答案】(1)定义域为
设
① 当时,对称轴,,所以在上是增函数 -----------------------------2分
② 当时,,所以在上是增函数 ----------------------------------------4分
③ 当时,令得
令解得;令解得
所以的单调递增区间和;的单调递减区间
------------------------------------6分
(2)可化为(※)
设,由(1)知:
① 当时,在上是增函数
若时,;所以
若时,。所以
所以,当时,※式成立--------------------------------------10分
② 当时,在是减函数,所以※式不成立
综上,实数的取值范围是.----------------------------12分
解法二 :可化为
设
令
,
所以
在
由洛必达法则
所以
22.(本题满分10分)选修4—1几何证明选讲:
【答案】(1)
又切圆于点,
而(同弧)
所以,BD平分∠ABC——————————5分
(2)由(1)知,又,
又为公共角,所以与相似。
,因为AB=4,AD=6,BD=8,所以AH=3————————10分
23.(本题满分10分)选修4—4:坐标系与参数方程
【答案】解:(Ⅰ). ……………4分
(Ⅱ)直线的参数方程为(为参数),
代入, 得到, ………7分
则有.
因为,所以. 解得 .…10分
24.(本题满分10分)选修4—5:不等式选讲
同课章节目录
