【解析版】河南省十所名校2013届高三第三次联考数学(理)试题
文档属性
| 名称 | 【解析版】河南省十所名校2013届高三第三次联考数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 462.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-12 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
( http: / / www.21cnjy.com )
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.设全集U是实数集R,集合M={x|>2x},N={x|≤0},则(CUM)∩N=( )
A.{x|1<x<2} B.{x|1≤x≤2}
C.{x|1<x<≤2} D.{x|1<x<2}
( http: / / www.21cnjy.com )
2.对任意复数z=a+bi(a,b ∈R),i为虚数单位,则下列结论中正确的是( )
A. z-=2a B.z·=|z|2 C.=1 D.≥0
( http: / / www.21cnjy.com )
3.双曲线的离心率为( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
4.某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的
极差与中位数之和为( )
( http: / / www.21cnjy.com )
5.在△ABC中,M是AB边所在直线上任意一点,若=-2+λ,则λ=( )
A.1 B.2 C.3 D.421教育网
( http: / / www.21cnjy.com )
6.公差不为0的等差数列{}的前21项的和等于前8项的和.若,则k=( )
A.20 B.21 C.22 D.23www.21-cn-jy.com
( http: / / www.21cnjy.com )考点:等差数列的性质.
7.设函数f(x)=-lnx,则y=f(x)( )
A.在区间(,1),(1,e)内均有零点
B.在区间(,1),(1,e)内均无零点
C.在区间(,1)内有零点,在区间(1,e)内无零点
D.在区间(,1)内无零点,在区间(1,e)内有零点
( http: / / www.21cnjy.com )
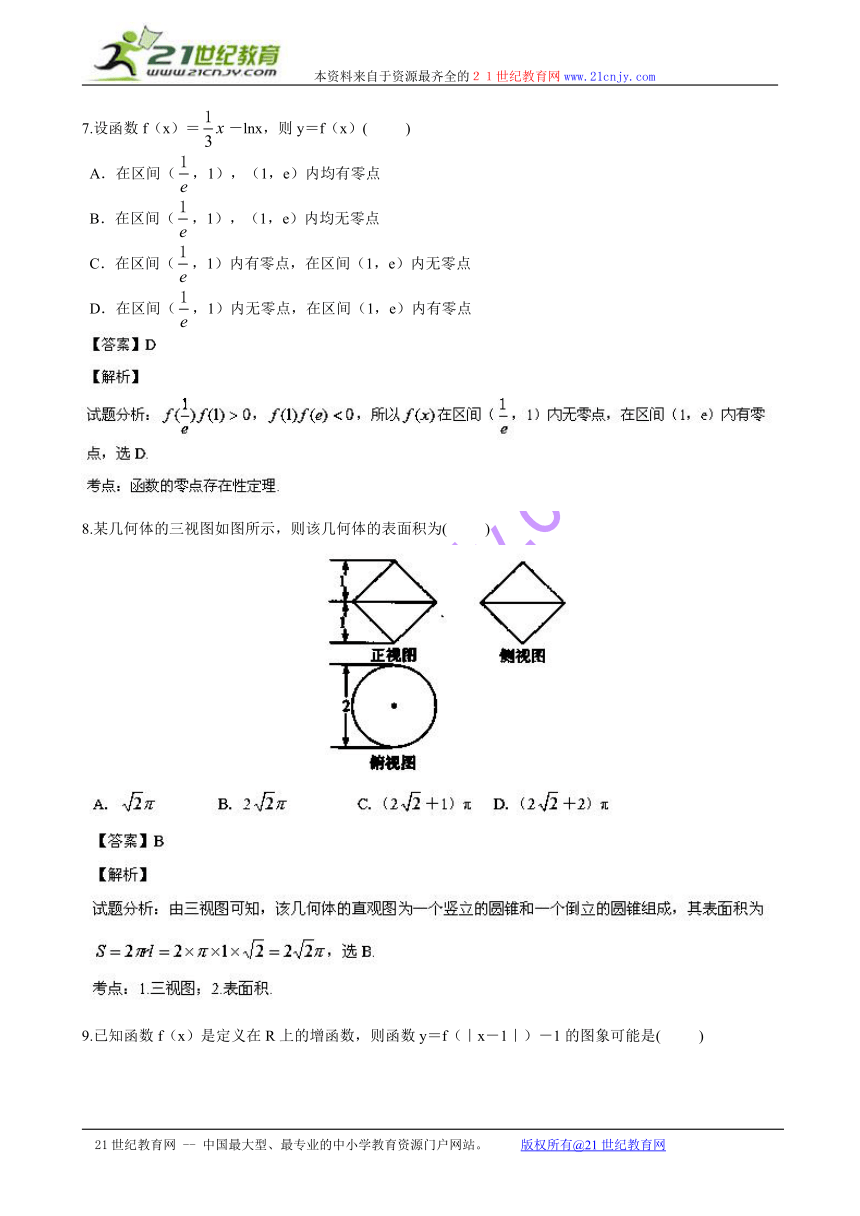
8.某几何体的三视图如图所示,则该几何体的表面积为( )
( http: / / www.21cnjy.com )
9.已知函数f(x)是定义在R上的增函数,则函数y=f(|x-1|)-1的图象可能是( )
( http: / / www.21cnjy.com )
10.在△ABC中,a,b,c分别是角A,B,C的对边,若=2014,则
的值为( )
A.0 B.1 C.2013 D.20142·1·c·n·j·y
( http: / / www.21cnjy.com )
11.若=+++…+(x∈R),则+++…+
( )
A.- B. C.- D.
( http: / / www.21cnjy.com ),所以,所以+++…+ ( http: / / www.21cnjy.com )
12.四面体ABCD中,AD与BC互相垂直,AD=2BC=4,且AB+BD=AC+CD=2,则
四面体ABCD的体积的最大值是( )
A.4 B.2 C.5 D.21世纪教育网版权所有
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.圆-2x+my-2=0关于抛物线=4y的准线对称,则m=_____________.
( http: / / www.21cnjy.com )
试题分析:易知,圆心坐标为,抛物线的准线方程为,依题意有,所以.
考点:1.圆的性质;2.抛物线的性质.
14.已知不等式组所表示的平面区域为D,若直线与平面区域D有公共点,则k的取值范围为 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
15.运行如下程序框图对应的程序,输出的结果是_______.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
16.设数列{}是等差数列,数列{}是等比数列,记数列{},{}的前n项和分别为,.若a5=b5,a6=b6,且S7-S5=4(T6-T4),则=____________.21·cn·jy·com
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)
已知函数f(x)=cos(2x-)+sin2x-cos2x.
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )当时,取得最大值2,
( http: / / www.21cnjy.com )
18.(本小题满分12分)
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:21cnjy.com
( http: / / www.21cnjy.com )
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少 [
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
1 求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
( http: / / www.21cnjy.com )
19.(本小题满分12分)
如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED为正方形,且所在平面垂直于平面ABC.21·世纪*教育网
(Ⅰ)证明:平面ADE∥平面BCF;
(Ⅱ)求二面角D-AE-F的正切值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
20.(本小题满分12分)
已知圆C:的半径等于椭圆E:(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-的距离为-,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).【来源:21·世纪·教育·网】
(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:|AF|-|BF|=|BM|-|AM|.
( http: / / www.21cnjy.com ),………………………………………………(2分)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21.(本小题满分12分)
对于函数f(x)(x∈D),若x∈D时,恒有>成立,则称函数是D上的J函数.
(Ⅰ)当函数f(x)=mlnx是J函数时,求m的取值范围;
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,
1 试比较g(a)与g(1)的大小;
2 求证:对于任意大于1的实数x1,x2,x3,…,xn,均有g(ln(x1+x2+…+xn))
>g(lnx1)+g(lnx2)+…+g(lnxn).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.
22.本小题满分10分)选修4—1:几何证明选讲
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.www-2-1-cnjy-com
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
( http: / / www.21cnjy.com )
23.(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为ρcos(θ-)=-1,曲线C2的极坐标方程为ρ=
2cos(θ-).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
( http: / / www.21cnjy.com )即可得;(Ⅱ)先化简得的直角坐标方程为,再求的圆心 ( http: / / www.21cnjy.com )
24.(本小题满分10分)选修4—5:不等式选讲
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求a的取值范围.
( http: / / www.21cnjy.com )试题解析:(Ⅰ)当时,不等式即为,
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
( http: / / www.21cnjy.com )
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.设全集U是实数集R,集合M={x|>2x},N={x|≤0},则(CUM)∩N=( )
A.{x|1<x<2} B.{x|1≤x≤2}
C.{x|1<x<≤2} D.{x|1<x<2}
( http: / / www.21cnjy.com )
2.对任意复数z=a+bi(a,b ∈R),i为虚数单位,则下列结论中正确的是( )
A. z-=2a B.z·=|z|2 C.=1 D.≥0
( http: / / www.21cnjy.com )
3.双曲线的离心率为( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
4.某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的
极差与中位数之和为( )
( http: / / www.21cnjy.com )
5.在△ABC中,M是AB边所在直线上任意一点,若=-2+λ,则λ=( )
A.1 B.2 C.3 D.421教育网
( http: / / www.21cnjy.com )
6.公差不为0的等差数列{}的前21项的和等于前8项的和.若,则k=( )
A.20 B.21 C.22 D.23www.21-cn-jy.com
( http: / / www.21cnjy.com )考点:等差数列的性质.
7.设函数f(x)=-lnx,则y=f(x)( )
A.在区间(,1),(1,e)内均有零点
B.在区间(,1),(1,e)内均无零点
C.在区间(,1)内有零点,在区间(1,e)内无零点
D.在区间(,1)内无零点,在区间(1,e)内有零点
( http: / / www.21cnjy.com )
8.某几何体的三视图如图所示,则该几何体的表面积为( )
( http: / / www.21cnjy.com )
9.已知函数f(x)是定义在R上的增函数,则函数y=f(|x-1|)-1的图象可能是( )
( http: / / www.21cnjy.com )
10.在△ABC中,a,b,c分别是角A,B,C的对边,若=2014,则
的值为( )
A.0 B.1 C.2013 D.20142·1·c·n·j·y
( http: / / www.21cnjy.com )
11.若=+++…+(x∈R),则+++…+
( )
A.- B. C.- D.
( http: / / www.21cnjy.com ),所以,所以+++…+ ( http: / / www.21cnjy.com )
12.四面体ABCD中,AD与BC互相垂直,AD=2BC=4,且AB+BD=AC+CD=2,则
四面体ABCD的体积的最大值是( )
A.4 B.2 C.5 D.21世纪教育网版权所有
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.圆-2x+my-2=0关于抛物线=4y的准线对称,则m=_____________.
( http: / / www.21cnjy.com )
试题分析:易知,圆心坐标为,抛物线的准线方程为,依题意有,所以.
考点:1.圆的性质;2.抛物线的性质.
14.已知不等式组所表示的平面区域为D,若直线与平面区域D有公共点,则k的取值范围为 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
15.运行如下程序框图对应的程序,输出的结果是_______.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
16.设数列{}是等差数列,数列{}是等比数列,记数列{},{}的前n项和分别为,.若a5=b5,a6=b6,且S7-S5=4(T6-T4),则=____________.21·cn·jy·com
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)
已知函数f(x)=cos(2x-)+sin2x-cos2x.
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )当时,取得最大值2,
( http: / / www.21cnjy.com )
18.(本小题满分12分)
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:21cnjy.com
( http: / / www.21cnjy.com )
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少 [
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
1 求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
( http: / / www.21cnjy.com )
19.(本小题满分12分)
如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED为正方形,且所在平面垂直于平面ABC.21·世纪*教育网
(Ⅰ)证明:平面ADE∥平面BCF;
(Ⅱ)求二面角D-AE-F的正切值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
20.(本小题满分12分)
已知圆C:的半径等于椭圆E:(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-的距离为-,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).【来源:21·世纪·教育·网】
(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:|AF|-|BF|=|BM|-|AM|.
( http: / / www.21cnjy.com ),………………………………………………(2分)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21.(本小题满分12分)
对于函数f(x)(x∈D),若x∈D时,恒有>成立,则称函数是D上的J函数.
(Ⅰ)当函数f(x)=mlnx是J函数时,求m的取值范围;
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,
1 试比较g(a)与g(1)的大小;
2 求证:对于任意大于1的实数x1,x2,x3,…,xn,均有g(ln(x1+x2+…+xn))
>g(lnx1)+g(lnx2)+…+g(lnxn).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.
22.本小题满分10分)选修4—1:几何证明选讲
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.www-2-1-cnjy-com
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
( http: / / www.21cnjy.com )
23.(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为ρcos(θ-)=-1,曲线C2的极坐标方程为ρ=
2cos(θ-).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
( http: / / www.21cnjy.com )即可得;(Ⅱ)先化简得的直角坐标方程为,再求的圆心 ( http: / / www.21cnjy.com )
24.(本小题满分10分)选修4—5:不等式选讲
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求a的取值范围.
( http: / / www.21cnjy.com )试题解析:(Ⅰ)当时,不等式即为,
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
