2022-2023学年北师大版八年级数学下册第一单元三角形的证明解答题(含解析)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册第一单元三角形的证明解答题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 401.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览

文档简介
北师版八年级第二学期第一单元三角形的证明解答题
1、如图,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
2、已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
3、已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.求证:AC﹣AB=2BE.
4、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.
5、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
5、如图,在等腰△ABC中,AB=AC,BD为高.(从下列两问中任选一问作答).(1)若∠ABD+∠C=120°,求∠A的度数.(2)若CD=3,BC=5,求△ABC的面积.
6、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.
7、如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.
8、如图,在平面直角坐标系xOy中,正比例函数的图象为直线l,已知两点A(0,1)、B(0,3).
(1)在直线l位于第一象限的部分找一点C,使得∠CAB=∠CBA.用直尺和圆规作出点C(不写画法,保留作图痕迹);(2)直接写出点C的坐标为 ;(3)点P在x轴上,求PA+PC的最小值.
9、已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足.求证:().().
10、如图,△ABC是等边三角形.(1)如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
11、如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1);(2)为等腰三角形.
12、如图,在中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为线段CE的中点,,.求证:.
13、已知,如图,AD∥BE,C为BE上一点,CD与AE相交于点F,连接AC.∠1=∠2,∠3=∠4.
(1)求证:AB∥CD;(2)已知AE=12cm,AB=5cm,BE=13cm,求AC的长度.
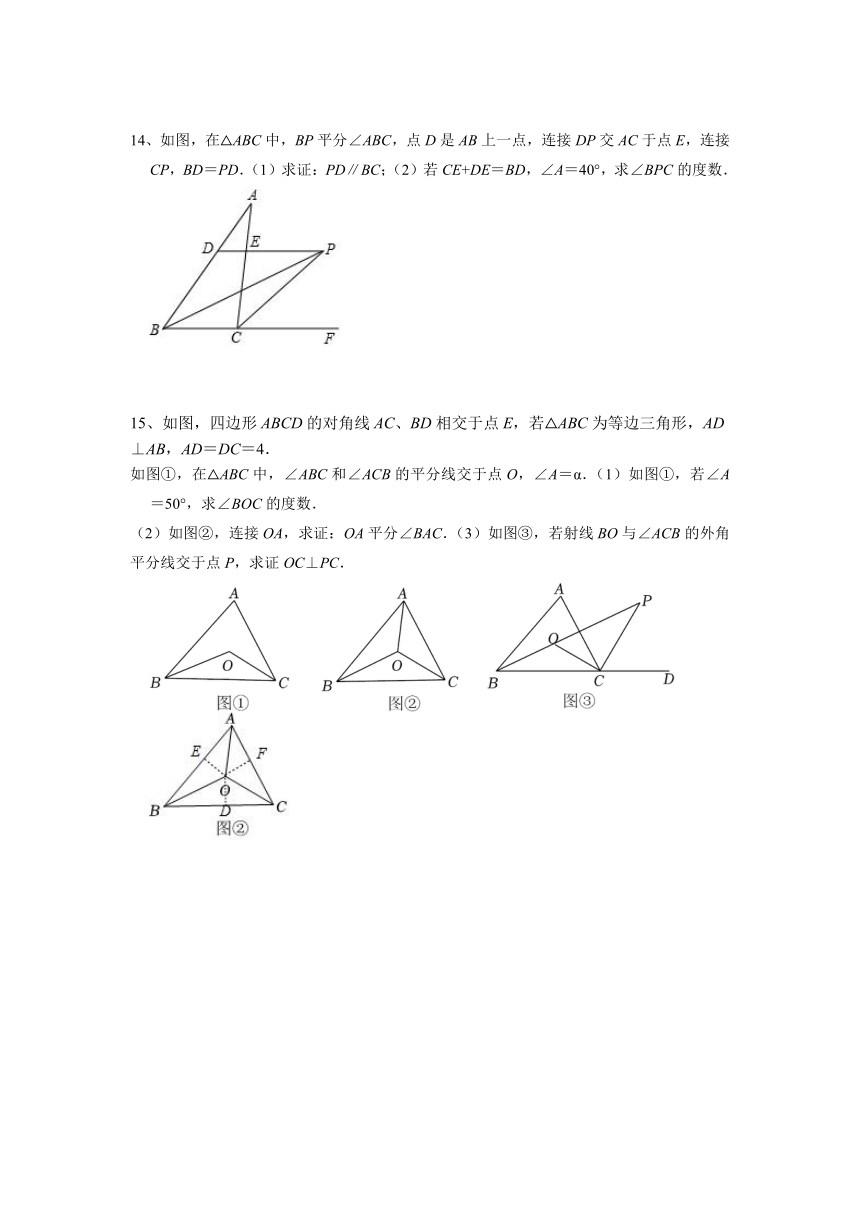
14、如图,在△ABC中,BP平分∠ABC,点D是AB上一点,连接DP交AC于点E,连接CP,BD=PD.(1)求证:PD∥BC;(2)若CE+DE=BD,∠A=40°,求∠BPC的度数.
15、如图,四边形ABCD的对角线AC、BD相交于点E,若△ABC为等边三角形,AD⊥AB,AD=DC=4.
如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:OA平分∠BAC.(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
北师版八年级第二学期第一单元三角形的证明解答题答案
1、如图,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
证明:∵∠CAE+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD.∵∠ADB=∠AEC=90°,AB=AC,
∴△ABD≌△CAE.∴AD=CE,BD=AE.∵AE=AD+DE=CE+DE,∴BD=DE+CE.
2、已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
证明:∵EF∥BC,∴∠HEC=∠ECB,∵CE平分∠ACB,∴∠ECB=∠ECA,∴∠ECA=∠HEC
∴EH=HC,同理HC=HF,∴EH=HF.
3、已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.求证:AC﹣AB=2BE.
证明:延长BE交AC于M∵BE⊥AE,∴∠AEB=∠AEM=90°在△ABE中,∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1同理,∠4=90°﹣∠2∵∠1=∠2,∴∠3=∠4,∴AB=AM∵BE⊥AE,∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,∵∠4是△BCM的外角∴∠4=∠5+∠C∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5∴3∠C=∠4+∠5=2∠5+∠C∴∠5=∠C∴CM=BM∴AC﹣AB=BM=2BE
4、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.
(1)证明:∵AB=AC,∴∠B=∠C,在△DBE和△ECF中,,∴△DBE≌△ECF,
∴DE=FE,∴△DEF是等腰三角形;(2)∵△BDE≌△CEF,∴∠FEC=∠BDE,∴∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B(3)∵由(2)知△BDE≌△CEF,∴∠BDE=∠CEF,∴∠CEF+∠DEF=∠BDE+∠B,∴∠DEF=∠B,∴AB=AC,∠A=40°,∴∠DEF=∠B==70°.
5、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
证明:过点D作DG∥AC交BC于点G,如图所示.∵DG∥AC,∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,,∴△GDF≌△CEF(ASA),∴GD=CE.∵BD=CE,
∴BD=GD,∴∠B=∠DGB=∠ACB,∴△ABC是等腰三角形.
5、如图,在等腰△ABC中,AB=AC,BD为高.(从下列两问中任选一问作答).(1)若∠ABD+∠C=120°,求∠A的度数.(2)若CD=3,BC=5,求△ABC的面积.
解:(1)∵AB=AC,∴∠ABC=∠C,设∠ABD=x°,则∠A=(90﹣x)°,∠C=(120﹣x)°,在△ABC中:∠A+∠C+∠ABC=180°,即90﹣x+2(120﹣x)=180,解得x=50°,则∠A=90﹣x=40°;(2)∵BD为高.∴△ADC为直角三角形,∵BD=4,BC=5,∴CD=3,设AD为x,则AB=AC=3+x,在直角三角形△ADB中,AD2+BD2=AB2,即,x2+42=(x+3)2,解得x=,S△ABC=AC×BD×=.
6、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.
证明:(1)∵△ABC、△ADE是等边三角形,∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即:∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=EC,∵BD=BC+CD=AC+CD,∴CE=BD=AC+CD;(2)由(1)知:△BAD≌△CAE,∴∠ACE=∠ABD=60°,∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ECD=60°.
7、如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.
(1)证明:∵CO=CD,∠OCD=60°,∴△COD是等边三角形;(2)解:当α=150°,即∠BOC=150°时,△AOD是直角三角形.∵△BOC≌△ADC,∴∠ADC=∠BOC=150°,又∵△COD是等边三角形,
∴∠ODC=60°,∴∠ADO=90°,即△AOD是直角三角形;(3)解:①要使AO=AD,需∠AOD=∠ADO.∵∠AOD=360°﹣∠AOB﹣∠COD﹣α=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.∵∠AOD=190°﹣α,∠ADO=α﹣60°,∴∠OAD=180°﹣(∠AOD+∠ADO)=50°,∴α﹣60°=50°∴α=110°;③要使OD=AD,需∠OAD=∠AOD.∵190°﹣α=50°∴α=140°.
综上所述:当α的度数为125°,或110°,或140°时,△AOD是等腰三角形.
8、如图,在平面直角坐标系xOy中,正比例函数的图象为直线l,已知两点A(0,1)、B(0,3).
(1)在直线l位于第一象限的部分找一点C,使得∠CAB=∠CBA.用直尺和圆规作出点C(不写画法,保留作图痕迹);(2)直接写出点C的坐标为 ;(3)点P在x轴上,求PA+PC的最小值.
解:(1)作线段AB的垂直平分线交直线l于点C即为所求,∵CD是线段AB的垂直平分线,∴CA=CB,∴∠CAB=∠CBA;(2)∵CD是线段AB的垂直平分线,∴点D是线段AB的中点,CD∥x轴,∵A(0,1)、B(0,3).∴D(0,2),将y=2代入y=x得x=4,∴点C的坐标为(4,2),故答案为:(4,2);
(3)作点A关于x轴的对称点,连接交x轴于点P,∴,
∴要使最小,即最小,∴当、,三点共线时,最小,最小值为,
∵A(0,1),∴(0,﹣1),∵C(4,2),∴,∴PA+PC的最小值是5.
9、已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足.求证:().().
解:证明:()∵为的角平分线,∴,∴在和中,
,∴≌,∴,∵,
,,∴,∴为等腰三角形,
∴,∵≌,∴,∴.
()过点作于点,∵是上的点,,,
∴,∵在和中,,∴≌,
∴,∵在和中,,≌,
∴,∴,,∴.
10、如图,△ABC是等边三角形.(1)如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
(1)证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∵DE∥BC,∴∠ADE=∠B=60°,∠AED=∠C=60°,∴△ADE是等边三角形;
(2)解:AE+CE=BE.∵∠BAD+∠DAC=60°,∠CAE+∠DAC=60°,∴∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,∠AEC=∠ADB=120°,
∴BE=BD+DE=AE+CE,∠BEC=∠AEC﹣∠AED=60°.
11、如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1);(2)为等腰三角形.
证明:(1),,.又BD是的平分线,,
,,又E是AB的中点,,即.
(2),,FE垂直平分AB,,.
又,.又,,
,,即为等腰三角形.
12、如图,在中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为线段CE的中点,,.求证:.
证明:连接AE,∵,,∴,
∴.∵点D为线段CE的中点,∴,∴AD垂直平分线段CE,
∴,∵EF垂直平分AB,∴,∴.
13、已知,如图,AD∥BE,C为BE上一点,CD与AE相交于点F,连接AC.∠1=∠2,∠3=∠4.
(1)求证:AB∥CD;(2)已知AE=12cm,AB=5cm,BE=13cm,求AC的长度.
(1)证明:∵AD∥BE,∴∠DAC=∠3,即∠2+∠EAC=∠3,∵∠1=∠2,∠3=∠4,
∴∠1+∠EAC=∠4,即∠BAE=∠4,∴AB∥CD;
(2)解:在△ABE中,AE=12cm,AB=5cm,BE=13cm,∴AE2+AB2=BE2,
∴△ABE为直角三角形,∠BAE=90°,由(1)得:∠4=∠BAE=90°,∴∠3=∠4=90°,
∴AC⊥BE,∵S△ABE=AE AB=BE AC,∴AC===(cm).
14、如图,在△ABC中,BP平分∠ABC,点D是AB上一点,连接DP交AC于点E,连接CP,BD=PD.(1)求证:PD∥BC;(2)若CE+DE=BD,∠A=40°,求∠BPC的度数.
(1)证明:∵BP平分∠ABC,∴∠ABP=∠FBP,∵BD=PD,∴∠ABP=BPD,∴∠BPD=∠FBP,
∴PD∥BC;
(2)解:∵PD∥BC,∴∠EPC=∠PCF,∵DP=DE+EP=BD=CE+DE,∴CE=EP,
∴∠EPC=∠ECP,∴∠PCE=∠PCF,∴∠BPC=∠PCF﹣∠BPD,==
==20°.
15、如图,四边形ABCD的对角线AC、BD相交于点E,若△ABC为等边三角形,AD⊥AB,AD=DC=4.
如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:OA平分∠BAC.(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
(1)解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=130°,∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,∴OD=OE,OD=OF,∴OE=OF,∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,∴OC⊥CP.
1、如图,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
2、已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
3、已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.求证:AC﹣AB=2BE.
4、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.
5、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
5、如图,在等腰△ABC中,AB=AC,BD为高.(从下列两问中任选一问作答).(1)若∠ABD+∠C=120°,求∠A的度数.(2)若CD=3,BC=5,求△ABC的面积.
6、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.
7、如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.
8、如图,在平面直角坐标系xOy中,正比例函数的图象为直线l,已知两点A(0,1)、B(0,3).
(1)在直线l位于第一象限的部分找一点C,使得∠CAB=∠CBA.用直尺和圆规作出点C(不写画法,保留作图痕迹);(2)直接写出点C的坐标为 ;(3)点P在x轴上,求PA+PC的最小值.
9、已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足.求证:().().
10、如图,△ABC是等边三角形.(1)如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
11、如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1);(2)为等腰三角形.
12、如图,在中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为线段CE的中点,,.求证:.
13、已知,如图,AD∥BE,C为BE上一点,CD与AE相交于点F,连接AC.∠1=∠2,∠3=∠4.
(1)求证:AB∥CD;(2)已知AE=12cm,AB=5cm,BE=13cm,求AC的长度.
14、如图,在△ABC中,BP平分∠ABC,点D是AB上一点,连接DP交AC于点E,连接CP,BD=PD.(1)求证:PD∥BC;(2)若CE+DE=BD,∠A=40°,求∠BPC的度数.
15、如图,四边形ABCD的对角线AC、BD相交于点E,若△ABC为等边三角形,AD⊥AB,AD=DC=4.
如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:OA平分∠BAC.(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
北师版八年级第二学期第一单元三角形的证明解答题答案
1、如图,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
证明:∵∠CAE+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD.∵∠ADB=∠AEC=90°,AB=AC,
∴△ABD≌△CAE.∴AD=CE,BD=AE.∵AE=AD+DE=CE+DE,∴BD=DE+CE.
2、已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EF∥BC,分别交AC、CF于点H、F.求证:EH=HF.
证明:∵EF∥BC,∴∠HEC=∠ECB,∵CE平分∠ACB,∴∠ECB=∠ECA,∴∠ECA=∠HEC
∴EH=HC,同理HC=HF,∴EH=HF.
3、已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.求证:AC﹣AB=2BE.
证明:延长BE交AC于M∵BE⊥AE,∴∠AEB=∠AEM=90°在△ABE中,∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1同理,∠4=90°﹣∠2∵∠1=∠2,∴∠3=∠4,∴AB=AM∵BE⊥AE,∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,∵∠4是△BCM的外角∴∠4=∠5+∠C∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5∴3∠C=∠4+∠5=2∠5+∠C∴∠5=∠C∴CM=BM∴AC﹣AB=BM=2BE
4、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.
(1)证明:∵AB=AC,∴∠B=∠C,在△DBE和△ECF中,,∴△DBE≌△ECF,
∴DE=FE,∴△DEF是等腰三角形;(2)∵△BDE≌△CEF,∴∠FEC=∠BDE,∴∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B(3)∵由(2)知△BDE≌△CEF,∴∠BDE=∠CEF,∴∠CEF+∠DEF=∠BDE+∠B,∴∠DEF=∠B,∴AB=AC,∠A=40°,∴∠DEF=∠B==70°.
5、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
证明:过点D作DG∥AC交BC于点G,如图所示.∵DG∥AC,∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,,∴△GDF≌△CEF(ASA),∴GD=CE.∵BD=CE,
∴BD=GD,∴∠B=∠DGB=∠ACB,∴△ABC是等腰三角形.
5、如图,在等腰△ABC中,AB=AC,BD为高.(从下列两问中任选一问作答).(1)若∠ABD+∠C=120°,求∠A的度数.(2)若CD=3,BC=5,求△ABC的面积.
解:(1)∵AB=AC,∴∠ABC=∠C,设∠ABD=x°,则∠A=(90﹣x)°,∠C=(120﹣x)°,在△ABC中:∠A+∠C+∠ABC=180°,即90﹣x+2(120﹣x)=180,解得x=50°,则∠A=90﹣x=40°;(2)∵BD为高.∴△ADC为直角三角形,∵BD=4,BC=5,∴CD=3,设AD为x,则AB=AC=3+x,在直角三角形△ADB中,AD2+BD2=AB2,即,x2+42=(x+3)2,解得x=,S△ABC=AC×BD×=.
6、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.
证明:(1)∵△ABC、△ADE是等边三角形,∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即:∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=EC,∵BD=BC+CD=AC+CD,∴CE=BD=AC+CD;(2)由(1)知:△BAD≌△CAE,∴∠ACE=∠ABD=60°,∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ECD=60°.
7、如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.
(1)证明:∵CO=CD,∠OCD=60°,∴△COD是等边三角形;(2)解:当α=150°,即∠BOC=150°时,△AOD是直角三角形.∵△BOC≌△ADC,∴∠ADC=∠BOC=150°,又∵△COD是等边三角形,
∴∠ODC=60°,∴∠ADO=90°,即△AOD是直角三角形;(3)解:①要使AO=AD,需∠AOD=∠ADO.∵∠AOD=360°﹣∠AOB﹣∠COD﹣α=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.∵∠AOD=190°﹣α,∠ADO=α﹣60°,∴∠OAD=180°﹣(∠AOD+∠ADO)=50°,∴α﹣60°=50°∴α=110°;③要使OD=AD,需∠OAD=∠AOD.∵190°﹣α=50°∴α=140°.
综上所述:当α的度数为125°,或110°,或140°时,△AOD是等腰三角形.
8、如图,在平面直角坐标系xOy中,正比例函数的图象为直线l,已知两点A(0,1)、B(0,3).
(1)在直线l位于第一象限的部分找一点C,使得∠CAB=∠CBA.用直尺和圆规作出点C(不写画法,保留作图痕迹);(2)直接写出点C的坐标为 ;(3)点P在x轴上,求PA+PC的最小值.
解:(1)作线段AB的垂直平分线交直线l于点C即为所求,∵CD是线段AB的垂直平分线,∴CA=CB,∴∠CAB=∠CBA;(2)∵CD是线段AB的垂直平分线,∴点D是线段AB的中点,CD∥x轴,∵A(0,1)、B(0,3).∴D(0,2),将y=2代入y=x得x=4,∴点C的坐标为(4,2),故答案为:(4,2);
(3)作点A关于x轴的对称点,连接交x轴于点P,∴,
∴要使最小,即最小,∴当、,三点共线时,最小,最小值为,
∵A(0,1),∴(0,﹣1),∵C(4,2),∴,∴PA+PC的最小值是5.
9、已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足.求证:().().
解:证明:()∵为的角平分线,∴,∴在和中,
,∴≌,∴,∵,
,,∴,∴为等腰三角形,
∴,∵≌,∴,∴.
()过点作于点,∵是上的点,,,
∴,∵在和中,,∴≌,
∴,∵在和中,,≌,
∴,∴,,∴.
10、如图,△ABC是等边三角形.(1)如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
(1)证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∵DE∥BC,∴∠ADE=∠B=60°,∠AED=∠C=60°,∴△ADE是等边三角形;
(2)解:AE+CE=BE.∵∠BAD+∠DAC=60°,∠CAE+∠DAC=60°,∴∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,∠AEC=∠ADB=120°,
∴BE=BD+DE=AE+CE,∠BEC=∠AEC﹣∠AED=60°.
11、如图,在中,,,BD是的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1);(2)为等腰三角形.
证明:(1),,.又BD是的平分线,,
,,又E是AB的中点,,即.
(2),,FE垂直平分AB,,.
又,.又,,
,,即为等腰三角形.
12、如图,在中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为线段CE的中点,,.求证:.
证明:连接AE,∵,,∴,
∴.∵点D为线段CE的中点,∴,∴AD垂直平分线段CE,
∴,∵EF垂直平分AB,∴,∴.
13、已知,如图,AD∥BE,C为BE上一点,CD与AE相交于点F,连接AC.∠1=∠2,∠3=∠4.
(1)求证:AB∥CD;(2)已知AE=12cm,AB=5cm,BE=13cm,求AC的长度.
(1)证明:∵AD∥BE,∴∠DAC=∠3,即∠2+∠EAC=∠3,∵∠1=∠2,∠3=∠4,
∴∠1+∠EAC=∠4,即∠BAE=∠4,∴AB∥CD;
(2)解:在△ABE中,AE=12cm,AB=5cm,BE=13cm,∴AE2+AB2=BE2,
∴△ABE为直角三角形,∠BAE=90°,由(1)得:∠4=∠BAE=90°,∴∠3=∠4=90°,
∴AC⊥BE,∵S△ABE=AE AB=BE AC,∴AC===(cm).
14、如图,在△ABC中,BP平分∠ABC,点D是AB上一点,连接DP交AC于点E,连接CP,BD=PD.(1)求证:PD∥BC;(2)若CE+DE=BD,∠A=40°,求∠BPC的度数.
(1)证明:∵BP平分∠ABC,∴∠ABP=∠FBP,∵BD=PD,∴∠ABP=BPD,∴∠BPD=∠FBP,
∴PD∥BC;
(2)解:∵PD∥BC,∴∠EPC=∠PCF,∵DP=DE+EP=BD=CE+DE,∴CE=EP,
∴∠EPC=∠ECP,∴∠PCE=∠PCF,∴∠BPC=∠PCF﹣∠BPD,==
==20°.
15、如图,四边形ABCD的对角线AC、BD相交于点E,若△ABC为等边三角形,AD⊥AB,AD=DC=4.
如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:OA平分∠BAC.(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
(1)解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=130°,∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,∴OD=OE,OD=OF,∴OE=OF,∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,∴OC⊥CP.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
