6.3.1 实数导学案【人教版七下数学精品备课】
文档属性
| 名称 | 6.3.1 实数导学案【人教版七下数学精品备课】 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学段 初中 年级 七年级 学科 数 学
单元 第6单元 课题 6.3.1实数 课型 新授
核心 素养 课标 1、了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值。 2、能用有理数估计一个无理数的大致范围
教学 目标 1. 了解无理数和实数的概念 2.会对实数按照一定的标准进行分类;知道实数和数轴上的点的关系.能估算无理数的大小 3.了解实数范围内相反数和绝对值的意义
教学 重点 正确理解实数的概念
教学 难点 理解实数的概念; 体会数轴上的点与实数是一一对应的.
导学 环节 课堂 流程 时间 任务驱动 问题导学 学法 指导 知识 链接
呈现 目标 用小黑板呈现本节课的学习目标,并让学生诵读
自主学习 温故 知新 2 2、是这样的数么
互助 释疑 2 1、什么是有理数 如何分类 (板书)
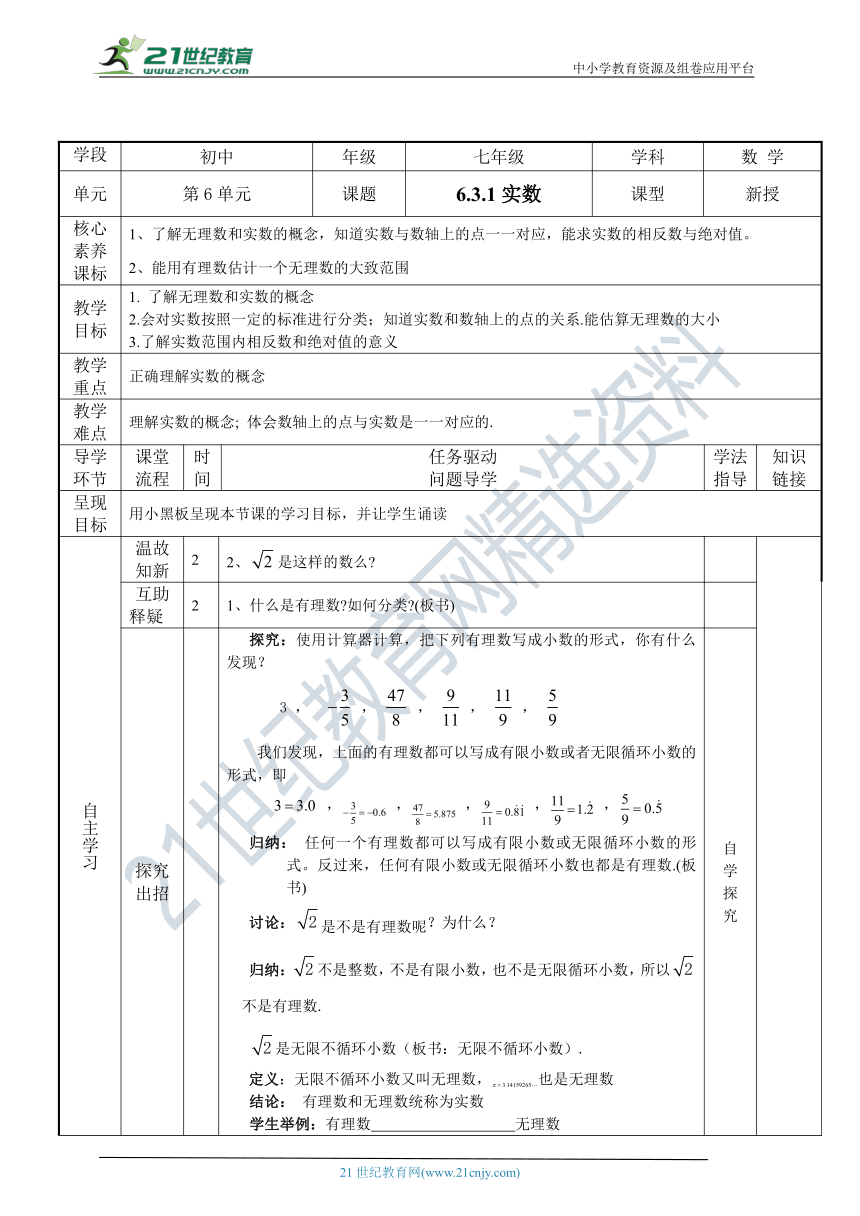
探究 出招 21 探究:使用计算器计算,把下列有理数写成小数的形式,你有什么发现? 3 , , , , , 我们发现,上面的有理数都可以写成有限小数或者无限循环小数的形式,即 , , , , , 归纳: 任何一个有理数都可以写成有限小数或无限循环小数的形式。反过来,任何有限小数或无限循环小数也都是有理数.(板书) 讨论:是不是有理数呢?为什么? 归纳:不是整数,不是有限小数,也不是无限循环小数,所以不是有理数. 是无限不循环小数(板书:无限不循环小数). 定义:无限不循环小数又叫无理数,也是无理数 结论: 有理数和无理数统称为实数 学生举例:有理数 无理数 整理: 如:填空: 在-19,3.878787…,,,,1.414,,,这些数中, 有理数是 ; 无理数是 ; 【活动2】 我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢? 探究 1. 1.如图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少? 2. 总结: ①事实上,每一个无理数都可以用数轴上的________表示出来,这就是说,数轴上的点有些表示______,有些表示_________ 当从有理数扩充到实数以后,实数与数轴上的点就是__________的,即每一个实数都可以用数轴上的__________来表示;反过来,数轴上的__________都是表示一个实数 与有理数一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数______ 讨论: 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数吗? 总结 数的相反数是______,这里表示任意____________。一个正实数的绝对值是______;一个负实数的绝对值是它的______;0的绝对值是______ 自 学 探 究
展示交流 小组 展示 2 小组内交流如何在数轴上表示一个无理数。
班级 展示 2 每组选派一名代表在本组的展示板上展示如何在数轴上表示。
点拨升华 反馈 矫正 1 教师就学生的展示点拨
扩展 提升 3 课本P55例1
总结 提高 2 无理数的特征: 1.圆周率及一些含有的数 2.开不尽方的数 3.有一定的规律,但不循环的无限小数 注意:带根号的数不一定是无理数
课堂作业 达标 训练 5 课本p56练习第1、2、3题和习题6.3第1、2、3、7题毛
课堂小结 实数
课后 反思 本节课学习了实数的有关概念和实数的分类,把我们所学过的数在有理数的基础上扩充到实数.在学习中,要求学生结合有理数理解实数的有关概念.本节课要注意的地方有两个:一是所有的分数都是有理数,如;二是形如,等之类的含有π的数不是分数,而是无理数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
学段 初中 年级 七年级 学科 数 学
单元 第6单元 课题 6.3.1实数 课型 新授
核心 素养 课标 1、了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值。 2、能用有理数估计一个无理数的大致范围
教学 目标 1. 了解无理数和实数的概念 2.会对实数按照一定的标准进行分类;知道实数和数轴上的点的关系.能估算无理数的大小 3.了解实数范围内相反数和绝对值的意义
教学 重点 正确理解实数的概念
教学 难点 理解实数的概念; 体会数轴上的点与实数是一一对应的.
导学 环节 课堂 流程 时间 任务驱动 问题导学 学法 指导 知识 链接
呈现 目标 用小黑板呈现本节课的学习目标,并让学生诵读
自主学习 温故 知新 2 2、是这样的数么
互助 释疑 2 1、什么是有理数 如何分类 (板书)
探究 出招 21 探究:使用计算器计算,把下列有理数写成小数的形式,你有什么发现? 3 , , , , , 我们发现,上面的有理数都可以写成有限小数或者无限循环小数的形式,即 , , , , , 归纳: 任何一个有理数都可以写成有限小数或无限循环小数的形式。反过来,任何有限小数或无限循环小数也都是有理数.(板书) 讨论:是不是有理数呢?为什么? 归纳:不是整数,不是有限小数,也不是无限循环小数,所以不是有理数. 是无限不循环小数(板书:无限不循环小数). 定义:无限不循环小数又叫无理数,也是无理数 结论: 有理数和无理数统称为实数 学生举例:有理数 无理数 整理: 如:填空: 在-19,3.878787…,,,,1.414,,,这些数中, 有理数是 ; 无理数是 ; 【活动2】 我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢? 探究 1. 1.如图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少? 2. 总结: ①事实上,每一个无理数都可以用数轴上的________表示出来,这就是说,数轴上的点有些表示______,有些表示_________ 当从有理数扩充到实数以后,实数与数轴上的点就是__________的,即每一个实数都可以用数轴上的__________来表示;反过来,数轴上的__________都是表示一个实数 与有理数一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数______ 讨论: 当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数吗? 总结 数的相反数是______,这里表示任意____________。一个正实数的绝对值是______;一个负实数的绝对值是它的______;0的绝对值是______ 自 学 探 究
展示交流 小组 展示 2 小组内交流如何在数轴上表示一个无理数。
班级 展示 2 每组选派一名代表在本组的展示板上展示如何在数轴上表示。
点拨升华 反馈 矫正 1 教师就学生的展示点拨
扩展 提升 3 课本P55例1
总结 提高 2 无理数的特征: 1.圆周率及一些含有的数 2.开不尽方的数 3.有一定的规律,但不循环的无限小数 注意:带根号的数不一定是无理数
课堂作业 达标 训练 5 课本p56练习第1、2、3题和习题6.3第1、2、3、7题毛
课堂小结 实数
课后 反思 本节课学习了实数的有关概念和实数的分类,把我们所学过的数在有理数的基础上扩充到实数.在学习中,要求学生结合有理数理解实数的有关概念.本节课要注意的地方有两个:一是所有的分数都是有理数,如;二是形如,等之类的含有π的数不是分数,而是无理数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
