6.3.1实数 课件(共24张PPT)
图片预览







文档简介
(共24张PPT)
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
6.3.1实数
核心素养目标:
了解无理数和实数的概念;会对实数按照一定的标准进行分类,培养分类能力;
了解分类的标准与分类结果的相关性,进一步了解体会“集合”的含义;
了解实数范围内相反数和绝对值的意。
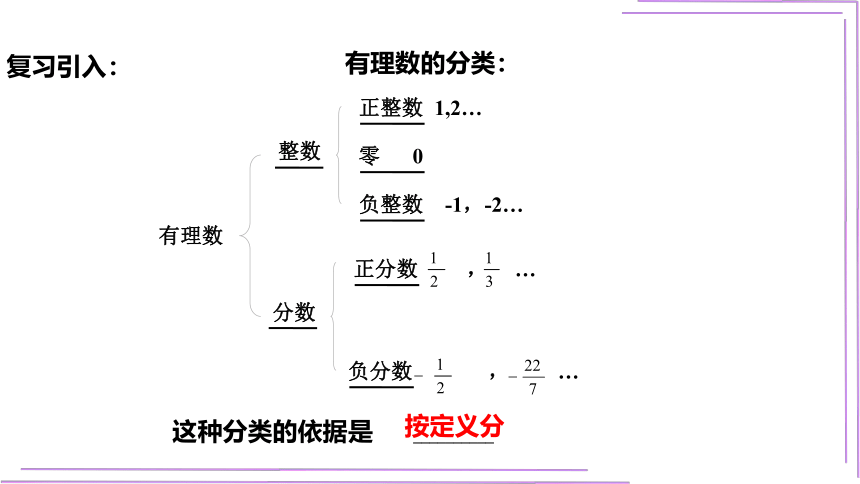
有理数
整数
分数
正整数 1,2…
零 0
负整数 -1,-2…
负分数 , …
正分数 , …
有理数的分类:
这种分类的依据是 __________
按定义分
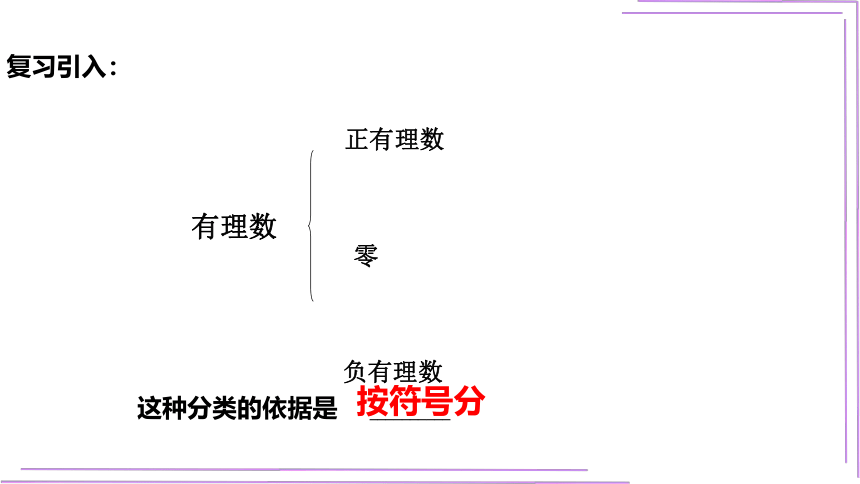
复习引入:
正有理数
零
负有理数
有理数
这种分类的依据是 __________
按符号分
复习引入:
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
互助探究:
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
互助探究:
新知讲解:
实数的概念
很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做无理数.有理数和无理数统称实数。
例如,,等都是无理数,=3.14159265……也是无理数.
仿照有理数的分类吗?你能给实数分类吗?
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
新知讲解:
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类:
新知讲解:
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
例题精讲:
思考:我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点表示出来呢?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,点0’对应的数是多少?
从图中可以看出,OO'的长是这个圆的周长式,所以点O’对应的数是π,这样,无理数π可以用数轴上的点表示出来.
.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
O’
互助探究:
互助探究:
-2
-1
0
1
2
-
思考:以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示,与负半轴的交点就表示.(为什么 )
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
实数
数轴上的点
一一对应
新知讲解:
原点
0
正实数
负实数
<
教材56页练习
1.请将图中数轴上标有字母的各点与下列实数对应起来:
4
-2
0
-1.5
π
3
跟踪练习:
2.在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
3.估计位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
跟踪练习:
实数
无理数的概念
实数的概念
实数的分类
实数的数轴表示
实数的大小比较
课堂小结:
1.判断快枪手——看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
课堂检测:
2.下列实数中,哪些是有理数?哪些是无理数?
5,3.14,0, , , , ,– π,
0.1010010001……(相邻两个1之间0的个数逐次加1).
课堂检测:
3. 估计 与6的大小.
解: 37 >36
> 6.
课堂检测:
课后作业:
必做题:57页习题6.3第1、2题;
选做题:57页习题6.3第6、7题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
6.3.1实数
核心素养目标:
了解无理数和实数的概念;会对实数按照一定的标准进行分类,培养分类能力;
了解分类的标准与分类结果的相关性,进一步了解体会“集合”的含义;
了解实数范围内相反数和绝对值的意。
有理数
整数
分数
正整数 1,2…
零 0
负整数 -1,-2…
负分数 , …
正分数 , …
有理数的分类:
这种分类的依据是 __________
按定义分
复习引入:
正有理数
零
负有理数
有理数
这种分类的依据是 __________
按符号分
复习引入:
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
互助探究:
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
互助探究:
新知讲解:
实数的概念
很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做无理数.有理数和无理数统称实数。
例如,,等都是无理数,=3.14159265……也是无理数.
仿照有理数的分类吗?你能给实数分类吗?
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
新知讲解:
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
也可以这样来分类:
新知讲解:
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
例题精讲:
思考:我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点表示出来呢?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,点0’对应的数是多少?
从图中可以看出,OO'的长是这个圆的周长式,所以点O’对应的数是π,这样,无理数π可以用数轴上的点表示出来.
.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
O’
互助探究:
互助探究:
-2
-1
0
1
2
-
思考:以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示,与负半轴的交点就表示.(为什么 )
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
实数
数轴上的点
一一对应
新知讲解:
原点
0
正实数
负实数
<
教材56页练习
1.请将图中数轴上标有字母的各点与下列实数对应起来:
4
-2
0
-1.5
π
3
跟踪练习:
2.在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
3.估计位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
跟踪练习:
实数
无理数的概念
实数的概念
实数的分类
实数的数轴表示
实数的大小比较
课堂小结:
1.判断快枪手——看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
课堂检测:
2.下列实数中,哪些是有理数?哪些是无理数?
5,3.14,0, , , , ,– π,
0.1010010001……(相邻两个1之间0的个数逐次加1).
课堂检测:
3. 估计 与6的大小.
解: 37 >36
> 6.
课堂检测:
课后作业:
必做题:57页习题6.3第1、2题;
选做题:57页习题6.3第6、7题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
