《交通中的线——平行与相交》(同步练习带答案)三年级下册数学青岛版五四学制
文档属性
| 名称 | 《交通中的线——平行与相交》(同步练习带答案)三年级下册数学青岛版五四学制 |
|
|
| 格式 | docx | ||
| 文件大小 | 159.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览




文档简介
青岛版数学三年级下册同步练习
《交通中的线——平行与相交》
学校:___________姓名:___________班级:___________
一、选择题
1.下列说法正确的是( )
A.永不相交的两条直线互相平行
B.两条直线不平行就相交
C.两条直线相交成直角,这两条直线互相垂直
2.如图中,小刚从A过马路,最短的路线是( ).
A. B. C.
3.如图中从点A到线段BE的线段中,最短的一条是( )
A.AE B.AD C.AC
4.从一点到已知直线的所有连线中,与已知直线垂直的线段有( )条?
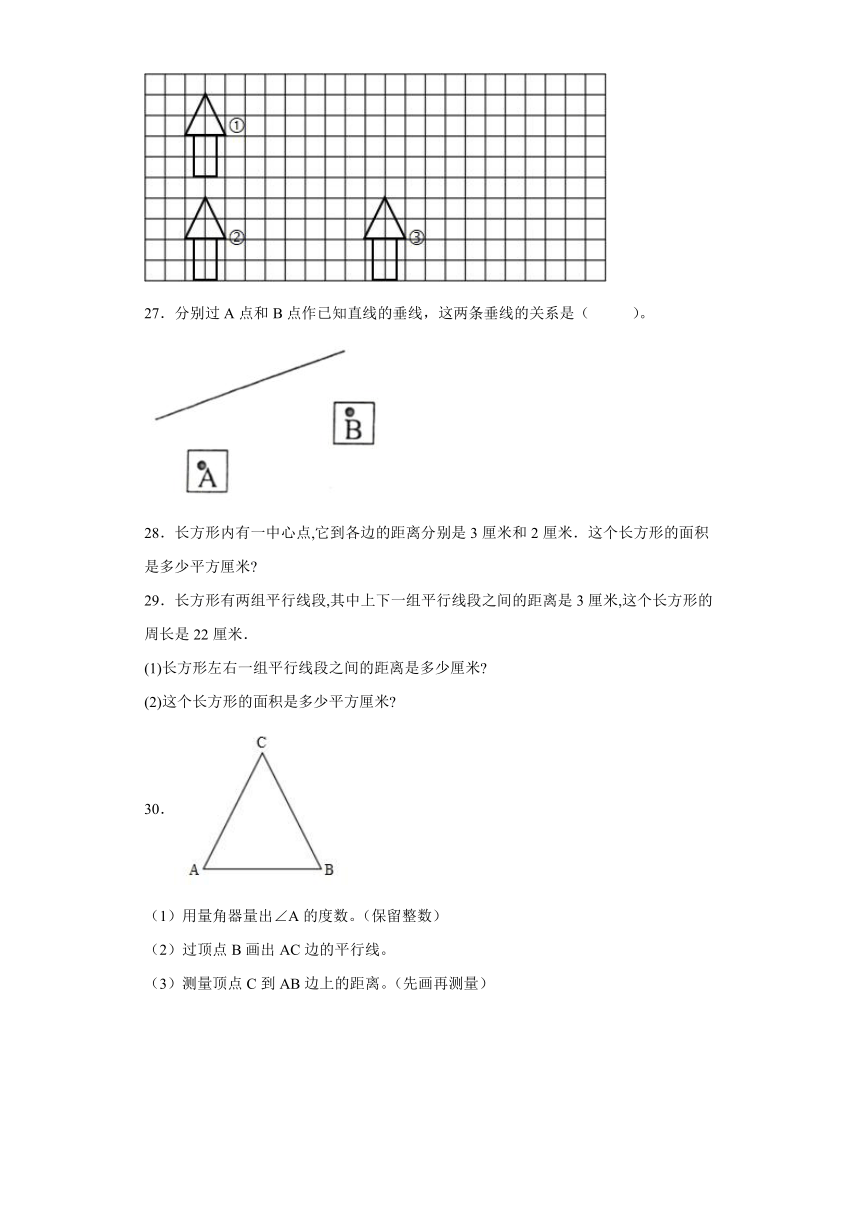
A.1条 B.2条 C.无数条
5.下列各组直线中, 组互相平行, 组互相垂直。( )
① ② ③
A.①② B.①③ C.③②
6.如下图,以下表达正确的是( )。
A.a⊥c B.a∥b C.a∥c
7.直线外一点到直线L的所有线段中,最短的是( )。
A.平行线 B.线段 C.垂线段
8.把一个长方形的纸,对折再对折,折线之间的关系是( )。
A.互相垂直 B.互相平行 C.以上都对
二、填空题
9.长方形的对边互相( ),邻边互相( );正方形的四条边( ),四个角都是( ). (前2个空填位置关系)
10.如果两条直线相交的夹角是90°,那么这两条直线相互________,其中一条是另一条的________,它们的交点叫做________。
11.连接两点间的所有连线中________最短,点到直线的垂直线段的长度叫做点到直线的________。
12.在公路上有三条小路通往小明家,它们的长度分别是100米、205米、112米,其中有一条小路于公路是垂直的,那么这条小路的长度是( )米。
13.在跳远比赛中,某运动员的起跳点为A,落地点为B,如图,量出落地点B到起跳点A所在直线l的距离BH,即为该运动员的成绩,此时,BH____BA(填“>”或“<”),理由:____。
14.比平角小125°的角是( )°,再加( )°就是直角。
15.过一点可以画( )条直线,过两点可以画( )直线;两条直线相交成直角时,这两条直线相互( )。同一平面内两条直线不相交,这两条直线相互( )。
16.下图这个网格正方形是用平行线画出的,共用了( )组平行线?在这个正方形中,共能找出( )组平行线。
三、判断题
17.在一张纸上画若干条直线后发现,凡是不平行的,就必然会相交。( )
18.如果第一条直线平行于第二条直线,第二条直线平行于第三条直线,则第一条直线垂直于第三条直线。( )
19.两条平行线中的其中一条直线绕一个点顺时针旋转90度后和另一条直线垂直. ( )
20.点到直线的距离有无数条,其中垂线最短。( )
21.同一平面内的两条直线不相交就一定平行。( )
四、作图题
22.过P点分别画出线段AB的平行线和垂线。
五、解答题
23.如图有ABC三个点,连接BC两点画一条线段,量出A点到这条线段的距离大约是多少厘米。
答:大约是 厘米。
24.
(1)过A点和B点分别作已知直线的垂线,并标注上垂足符号“”。
(2)画出的这两条垂线之间的位置关系是( )。
(3)估一估,A点到已知直线的距离大约是( )cm。(填写整数)
25.量一量,画一画。
(1)下图中点A到直线的距离是( )厘米。
(2)过A点画出已知直线的平行线。
26.请用简洁的话描述①到②的运动轨迹以及①到③的运动轨迹。
27.分别过A点和B点作已知直线的垂线,这两条垂线的关系是( )。
28.长方形内有一中心点,它到各边的距离分别是3厘米和2厘米.这个长方形的面积是多少平方厘米
29.长方形有两组平行线段,其中上下一组平行线段之间的距离是3厘米,这个长方形的周长是22厘米.
(1)长方形左右一组平行线段之间的距离是多少厘米
(2)这个长方形的面积是多少平方厘米
30.
(1)用量角器量出∠A的度数。(保留整数)
(2)过顶点B画出AC边的平行线。
(3)测量顶点C到AB边上的距离。(先画再测量)
参考答案:
1.C
【详解】略
2.B
【详解】因为从直线外一点到已知直线所作的所有线段中,垂线段最短,所以最短路线是B图..
3.B
【详解】图中过A点到直线BE的所有线段中,最短的一条是AD。
4.A
【解析】略
5.C
【详解】根据垂直和平行的意义可知,③组互相平行,②组互相垂直。
故答案为:C
6.A
【分析】垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
平行线的定义:在同一个平面内,不相交的两条直线叫做平行线。
【详解】观察图形可知,a⊥c,图中没有平行线。
故答案为选:A
7.C
【分析】根据点到直线的距离的含义:从直线外的一点向这条直线所画的垂直线段的长度,叫做这点到直线的距离;从直线外一点到这条直线所画的垂线段最短。
【详解】直线外一点到直线L的所有线段中,最短的是垂线段。
故答案为:C。
8.C
【分析】
如图所示,把一张长方形的纸对折两次共有两种情况,一种情况是沿一条边的同一方向对折两次,三条折痕是互相平行的。另一种情况是沿两条边的两个方向对折,两条折痕是互相垂直的。据此解答。
【详解】由分析得:把一个长方形的纸,对折再对折,折线之间的关系是可能垂直也可能平行。
故答案为:C。
【点睛】把一张长方形的纸对折两次,两次折痕的位置关系取决于对折的方向。根据垂直和平行的性质判断即可。
9. 平行 垂直 相等 直角
【解析】略
10. 垂直 垂线 垂足
【详解】同一平面内,相交成直角的两条直线互相垂直,可以说两条直线互相垂直,也可以说一条直线是另一条直线的垂线。
11. 线段 距离
【详解】略
12.100
【详解】把小明家看作一个点,公路看作一条直线,根垂直线段的性质,从直线外一点向直线所画的线中,垂直线段最短,三条小路中,到公路最短的一条与公路垂直。
如图
【点睛】此题主要是考查垂直线段的性质。从直线外一点向直线所画的线中,垂直线段最短。
13. < 垂线段最短
【详解】因为BH是点B到起跳点A所在直线l的垂线段,是最短的;所以BH<BA,理由:垂线段最短。
故答案为:<;垂线段最短。
14. 55 35
【分析】平角是180°,则比平角小125°的角是180°-125°=55°。直角是90°,则再加上(90°-55°)就是直角。
【详解】180°-125°=55°
90°-55°=35°
则比平角小125°的角是55°,再加35°就是直角。
【点睛】解决本题的关键是明确平角和直角的度数。
15. 无数 1条 垂直 平行
【分析】因为直线无端点,所以过一点可以画无数条直线;两点确定一条直线,所以过两点可以画1条直线;根据垂直的定义:如果两条直线相交成直角,就说这两条直线互相垂直;根据平行的定义:同一平面内两条直线不相交,这两条直线相互平行;据此解答即可。
【详解】过一点可以画无数条直线,过两点可以画1条直线;两条直线相交成直角时,这两条直线相互垂直。同一平面内两条直线不相交,这两条直线相互平行。
【点睛】此题考查的是直线的初步知识,以及垂直、平行的含义,平时应注意基础知识的积累。
16. 6 12
【分析】根据平行线的意义和特征进行观察判断即可解决。
【详解】①横着的平行线用了3组,竖着的平行线用了3组,共用了6组平行线;
②在这个正方形中,4条横线,两两平行,共能组成6组平行线,同理,竖着的平行线也有6组,共能找出12组平行线。
【点睛】解决本题的关键是正确理解平行线的意义和特征,根据图示找到平行线。
17.√
【详解】略
18.×
【分析】同一平面内,同平行与一条直线的两条直线是互相平行的;由此判断即可。
【详解】第一条直线和第三条直线都与第二条直线平行,那么第一条直线和第三条直线一定平行;原题说法错误。
故答案为:×
19.√
【详解】如下图:直线a绕O点顺时针旋转90°后得到直线b,这两条直线相交成直角,
它们互相垂直,所以本题说法正确;
故答案为√.
20.×
【分析】因为从直线外一点到已知直线的垂线段的长度叫做这点到已知直线的距离,据此即可解答。
【详解】点到直线的距离就是点到直线的垂线段的长度,有且只有一条。
故答案为:×
【点睛】本题主要是对点到直线的距离以及垂线段最短含义的考查,熟记概念一定要记准概念的外延与内涵。
21.√
【详解】在同一平面内的两条直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况,所以判断正确。
22.
【详解】(1)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可。
(2)把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和P点重合,过P点沿三角板的直角边,向已知直线画直线即可。
作图如下:
23.2;
【解析】略
24.(1)见详解
(2)互相平行
(3)2
【分析】(1)用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可,并标注垂足;同样的方法画出过B点到直线的垂线;
(2)在同一平面内的两直线垂直于同一条线,则这两条垂线相互平行;
(3)估测A点到直线的距离大约是2cm。
【详解】(1)
(2)画出的这两条垂线之间的位置关系是互相平行;
(3)A点到已知直线的距离大约是2cm。
【点睛】本题考查了学生过线外一点作垂线的能力,画出垂线是解题的关键。
25.(1)2;
(2)图见详解
【分析】(1)根据过直线外一点作已知直线的垂线的方法:把三角板的一条直角边与已知直线重合,沿这条直线滑动三角板,当另一个直角边经过已知点A时,沿这条直角边画直线,这条直线就是经过直线外一点的这条直线的垂线。再用直尺量出线段的长度即可;
(2)过直线外一点作已知直线的平行线的方法:把三角板的一边与已知直线重合,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线,这条直线就与已知直线平行。
【详解】(1)下图中点A到直线的距离是2厘米。
(2)
【点睛】本题主要考查点到直线的距离;连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
26.见解析
【详解】①到②:①向下平移5格到②。
①到③:方案一:①向下平移5格到②,再向右平移9格到③。
方案二:①向右平移9格,再向下平移5格到③。
27.互相平行;图见详解
【分析】过直线外(或直线上)一点作已知直线的垂线的方法是:把三角板的一条直角边靠紧已知直线,沿这条直线滑动三角板,当另一条直角边经过已知点时,沿这条直角边画直线,这条直线就是经过直线外一点的这条直线的垂线。过A、B两点分别画已知直线的垂线,这两条垂线是平行关系。
【详解】分别过A点和B点作已知直线的垂线,这两条垂线的关系是互相平行。
如图所示:
【点睛】本题主要考查垂线的画法,解答此题应明确:在同一平面内垂直于同一条直线的两条垂线互相平行。
28.24平方厘米
【详解】(3×2)×(2×2)
=6×4
=24(平方厘米)
答:这个长方形的面积是24平方厘米.
29.(1) 8厘米(2) 24平方厘米.
【详解】(1)22÷2-3
=11-3
=8(厘米)
答:长方形左右一组平行线段之间的距离是8厘米.
(2)8×3=24(平方厘米)
答:这个长方形的面积是24平方厘米.
30.(1)∠A=64°
(2)(3)画图见详解
3厘米1毫米
【分析】(1)量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可。
(3)从直线外一点到这条直线所画的垂直线段的长度叫这点到这条直线的距离。据此可知,过顶点C向AB作垂线,这条垂线即为顶点C到AB边上的距离,再用直尺量出这条垂线的长度即可。
【详解】(1)∠A=64°。
(2)(3)
顶点C到AB边上的距离是3厘米1毫米。
【点睛】本题考查用量角器量角的度数的方法以及平行和垂直的性质,旨在考查学生的作图能力。
《交通中的线——平行与相交》
学校:___________姓名:___________班级:___________
一、选择题
1.下列说法正确的是( )
A.永不相交的两条直线互相平行
B.两条直线不平行就相交
C.两条直线相交成直角,这两条直线互相垂直
2.如图中,小刚从A过马路,最短的路线是( ).
A. B. C.
3.如图中从点A到线段BE的线段中,最短的一条是( )
A.AE B.AD C.AC
4.从一点到已知直线的所有连线中,与已知直线垂直的线段有( )条?
A.1条 B.2条 C.无数条
5.下列各组直线中, 组互相平行, 组互相垂直。( )
① ② ③
A.①② B.①③ C.③②
6.如下图,以下表达正确的是( )。
A.a⊥c B.a∥b C.a∥c
7.直线外一点到直线L的所有线段中,最短的是( )。
A.平行线 B.线段 C.垂线段
8.把一个长方形的纸,对折再对折,折线之间的关系是( )。
A.互相垂直 B.互相平行 C.以上都对
二、填空题
9.长方形的对边互相( ),邻边互相( );正方形的四条边( ),四个角都是( ). (前2个空填位置关系)
10.如果两条直线相交的夹角是90°,那么这两条直线相互________,其中一条是另一条的________,它们的交点叫做________。
11.连接两点间的所有连线中________最短,点到直线的垂直线段的长度叫做点到直线的________。
12.在公路上有三条小路通往小明家,它们的长度分别是100米、205米、112米,其中有一条小路于公路是垂直的,那么这条小路的长度是( )米。
13.在跳远比赛中,某运动员的起跳点为A,落地点为B,如图,量出落地点B到起跳点A所在直线l的距离BH,即为该运动员的成绩,此时,BH____BA(填“>”或“<”),理由:____。
14.比平角小125°的角是( )°,再加( )°就是直角。
15.过一点可以画( )条直线,过两点可以画( )直线;两条直线相交成直角时,这两条直线相互( )。同一平面内两条直线不相交,这两条直线相互( )。
16.下图这个网格正方形是用平行线画出的,共用了( )组平行线?在这个正方形中,共能找出( )组平行线。
三、判断题
17.在一张纸上画若干条直线后发现,凡是不平行的,就必然会相交。( )
18.如果第一条直线平行于第二条直线,第二条直线平行于第三条直线,则第一条直线垂直于第三条直线。( )
19.两条平行线中的其中一条直线绕一个点顺时针旋转90度后和另一条直线垂直. ( )
20.点到直线的距离有无数条,其中垂线最短。( )
21.同一平面内的两条直线不相交就一定平行。( )
四、作图题
22.过P点分别画出线段AB的平行线和垂线。
五、解答题
23.如图有ABC三个点,连接BC两点画一条线段,量出A点到这条线段的距离大约是多少厘米。
答:大约是 厘米。
24.
(1)过A点和B点分别作已知直线的垂线,并标注上垂足符号“”。
(2)画出的这两条垂线之间的位置关系是( )。
(3)估一估,A点到已知直线的距离大约是( )cm。(填写整数)
25.量一量,画一画。
(1)下图中点A到直线的距离是( )厘米。
(2)过A点画出已知直线的平行线。
26.请用简洁的话描述①到②的运动轨迹以及①到③的运动轨迹。
27.分别过A点和B点作已知直线的垂线,这两条垂线的关系是( )。
28.长方形内有一中心点,它到各边的距离分别是3厘米和2厘米.这个长方形的面积是多少平方厘米
29.长方形有两组平行线段,其中上下一组平行线段之间的距离是3厘米,这个长方形的周长是22厘米.
(1)长方形左右一组平行线段之间的距离是多少厘米
(2)这个长方形的面积是多少平方厘米
30.
(1)用量角器量出∠A的度数。(保留整数)
(2)过顶点B画出AC边的平行线。
(3)测量顶点C到AB边上的距离。(先画再测量)
参考答案:
1.C
【详解】略
2.B
【详解】因为从直线外一点到已知直线所作的所有线段中,垂线段最短,所以最短路线是B图..
3.B
【详解】图中过A点到直线BE的所有线段中,最短的一条是AD。
4.A
【解析】略
5.C
【详解】根据垂直和平行的意义可知,③组互相平行,②组互相垂直。
故答案为:C
6.A
【分析】垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
平行线的定义:在同一个平面内,不相交的两条直线叫做平行线。
【详解】观察图形可知,a⊥c,图中没有平行线。
故答案为选:A
7.C
【分析】根据点到直线的距离的含义:从直线外的一点向这条直线所画的垂直线段的长度,叫做这点到直线的距离;从直线外一点到这条直线所画的垂线段最短。
【详解】直线外一点到直线L的所有线段中,最短的是垂线段。
故答案为:C。
8.C
【分析】
如图所示,把一张长方形的纸对折两次共有两种情况,一种情况是沿一条边的同一方向对折两次,三条折痕是互相平行的。另一种情况是沿两条边的两个方向对折,两条折痕是互相垂直的。据此解答。
【详解】由分析得:把一个长方形的纸,对折再对折,折线之间的关系是可能垂直也可能平行。
故答案为:C。
【点睛】把一张长方形的纸对折两次,两次折痕的位置关系取决于对折的方向。根据垂直和平行的性质判断即可。
9. 平行 垂直 相等 直角
【解析】略
10. 垂直 垂线 垂足
【详解】同一平面内,相交成直角的两条直线互相垂直,可以说两条直线互相垂直,也可以说一条直线是另一条直线的垂线。
11. 线段 距离
【详解】略
12.100
【详解】把小明家看作一个点,公路看作一条直线,根垂直线段的性质,从直线外一点向直线所画的线中,垂直线段最短,三条小路中,到公路最短的一条与公路垂直。
如图
【点睛】此题主要是考查垂直线段的性质。从直线外一点向直线所画的线中,垂直线段最短。
13. < 垂线段最短
【详解】因为BH是点B到起跳点A所在直线l的垂线段,是最短的;所以BH<BA,理由:垂线段最短。
故答案为:<;垂线段最短。
14. 55 35
【分析】平角是180°,则比平角小125°的角是180°-125°=55°。直角是90°,则再加上(90°-55°)就是直角。
【详解】180°-125°=55°
90°-55°=35°
则比平角小125°的角是55°,再加35°就是直角。
【点睛】解决本题的关键是明确平角和直角的度数。
15. 无数 1条 垂直 平行
【分析】因为直线无端点,所以过一点可以画无数条直线;两点确定一条直线,所以过两点可以画1条直线;根据垂直的定义:如果两条直线相交成直角,就说这两条直线互相垂直;根据平行的定义:同一平面内两条直线不相交,这两条直线相互平行;据此解答即可。
【详解】过一点可以画无数条直线,过两点可以画1条直线;两条直线相交成直角时,这两条直线相互垂直。同一平面内两条直线不相交,这两条直线相互平行。
【点睛】此题考查的是直线的初步知识,以及垂直、平行的含义,平时应注意基础知识的积累。
16. 6 12
【分析】根据平行线的意义和特征进行观察判断即可解决。
【详解】①横着的平行线用了3组,竖着的平行线用了3组,共用了6组平行线;
②在这个正方形中,4条横线,两两平行,共能组成6组平行线,同理,竖着的平行线也有6组,共能找出12组平行线。
【点睛】解决本题的关键是正确理解平行线的意义和特征,根据图示找到平行线。
17.√
【详解】略
18.×
【分析】同一平面内,同平行与一条直线的两条直线是互相平行的;由此判断即可。
【详解】第一条直线和第三条直线都与第二条直线平行,那么第一条直线和第三条直线一定平行;原题说法错误。
故答案为:×
19.√
【详解】如下图:直线a绕O点顺时针旋转90°后得到直线b,这两条直线相交成直角,
它们互相垂直,所以本题说法正确;
故答案为√.
20.×
【分析】因为从直线外一点到已知直线的垂线段的长度叫做这点到已知直线的距离,据此即可解答。
【详解】点到直线的距离就是点到直线的垂线段的长度,有且只有一条。
故答案为:×
【点睛】本题主要是对点到直线的距离以及垂线段最短含义的考查,熟记概念一定要记准概念的外延与内涵。
21.√
【详解】在同一平面内的两条直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况,所以判断正确。
22.
【详解】(1)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可。
(2)把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和P点重合,过P点沿三角板的直角边,向已知直线画直线即可。
作图如下:
23.2;
【解析】略
24.(1)见详解
(2)互相平行
(3)2
【分析】(1)用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可,并标注垂足;同样的方法画出过B点到直线的垂线;
(2)在同一平面内的两直线垂直于同一条线,则这两条垂线相互平行;
(3)估测A点到直线的距离大约是2cm。
【详解】(1)
(2)画出的这两条垂线之间的位置关系是互相平行;
(3)A点到已知直线的距离大约是2cm。
【点睛】本题考查了学生过线外一点作垂线的能力,画出垂线是解题的关键。
25.(1)2;
(2)图见详解
【分析】(1)根据过直线外一点作已知直线的垂线的方法:把三角板的一条直角边与已知直线重合,沿这条直线滑动三角板,当另一个直角边经过已知点A时,沿这条直角边画直线,这条直线就是经过直线外一点的这条直线的垂线。再用直尺量出线段的长度即可;
(2)过直线外一点作已知直线的平行线的方法:把三角板的一边与已知直线重合,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线,这条直线就与已知直线平行。
【详解】(1)下图中点A到直线的距离是2厘米。
(2)
【点睛】本题主要考查点到直线的距离;连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
26.见解析
【详解】①到②:①向下平移5格到②。
①到③:方案一:①向下平移5格到②,再向右平移9格到③。
方案二:①向右平移9格,再向下平移5格到③。
27.互相平行;图见详解
【分析】过直线外(或直线上)一点作已知直线的垂线的方法是:把三角板的一条直角边靠紧已知直线,沿这条直线滑动三角板,当另一条直角边经过已知点时,沿这条直角边画直线,这条直线就是经过直线外一点的这条直线的垂线。过A、B两点分别画已知直线的垂线,这两条垂线是平行关系。
【详解】分别过A点和B点作已知直线的垂线,这两条垂线的关系是互相平行。
如图所示:
【点睛】本题主要考查垂线的画法,解答此题应明确:在同一平面内垂直于同一条直线的两条垂线互相平行。
28.24平方厘米
【详解】(3×2)×(2×2)
=6×4
=24(平方厘米)
答:这个长方形的面积是24平方厘米.
29.(1) 8厘米(2) 24平方厘米.
【详解】(1)22÷2-3
=11-3
=8(厘米)
答:长方形左右一组平行线段之间的距离是8厘米.
(2)8×3=24(平方厘米)
答:这个长方形的面积是24平方厘米.
30.(1)∠A=64°
(2)(3)画图见详解
3厘米1毫米
【分析】(1)量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可。
(3)从直线外一点到这条直线所画的垂直线段的长度叫这点到这条直线的距离。据此可知,过顶点C向AB作垂线,这条垂线即为顶点C到AB边上的距离,再用直尺量出这条垂线的长度即可。
【详解】(1)∠A=64°。
(2)(3)
顶点C到AB边上的距离是3厘米1毫米。
【点睛】本题考查用量角器量角的度数的方法以及平行和垂直的性质,旨在考查学生的作图能力。
