专题7.15 平面直角坐标系(知识点分类专题)(巩固篇)(专项练习)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)
文档属性
| 名称 | 专题7.15 平面直角坐标系(知识点分类专题)(巩固篇)(专项练习)-2022-2023学年七年级数学下册基础知识专项讲练(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览



文档简介
专题7.15 平面直角坐标系(知识点分类专题)
(巩固篇)(专项练习)
一、单选题
【知识点1】有序数对
1.下列在具体情境中不能确定平面内位置的是( )
A.东经37°,北纬21° B.电影院某放映厅7排3号
C.鹤壁淇滨大道 D.外国语中学北偏东60°方向,2千米处
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
【知识点2】有序数对 规律问题 新定义
3.如图,将整数按规律排列,若有序数对(a,b)表示第a排从左往右第b个数,则(9,4)表示的数是( )
A.49 B.﹣40 C.﹣32 D.25
4.观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
A.(3,8) B.(4,7) C.(5,6) D.(6,5)
【知识点3】平面直角坐标系 点的坐标 点到坐标轴距离
5.已知点与点关于直线成轴对称,则点的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10, C.1, D.6,
【知识点4】平面直角坐标系 点的坐标 点所在的位置
7.若点在第一象限,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列说法正确的是( )
A.点在第四象限
B.若,则在坐标原点
C.点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为
D.在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为
【知识点5】平面直角坐标系 点所在的位置 求参数
9.在平面直角坐标系中,有三点,其中点A落在y轴上,P为直线AB上的一动点,若PC连线的长度最短,此时点P的坐标为( )
A. B. C. D.
10.在平面直角坐标系中,点在x轴上,则m的值为( )
A. B. C.1 D.3
【知识点6】平面直角坐标系 坐标系中描点
11.若有点A和点B,坐标分别为A(3,2),B(2,3),则( )
A.A,B为同一个点 B.A,B为重合的两点
C.A,B为不重合的两点 D.无法确定
12.在直角坐标系中,适合条件|x|=5,|x﹣y|=8的点P(x,y)的个数为( )
A.1 B.2 C.4 D.8
【知识点7】平面直角坐标系 坐标与面积
13.已知点,,点P在x轴上,且的面积为5,则点P的坐标是( )
A. B. C.或 D.或
14.已知点,点,点在轴上,若的面积为6,则点的坐标为( )
A. B. C. D.或
【知识点8】平面直角坐标系 坐标与图形
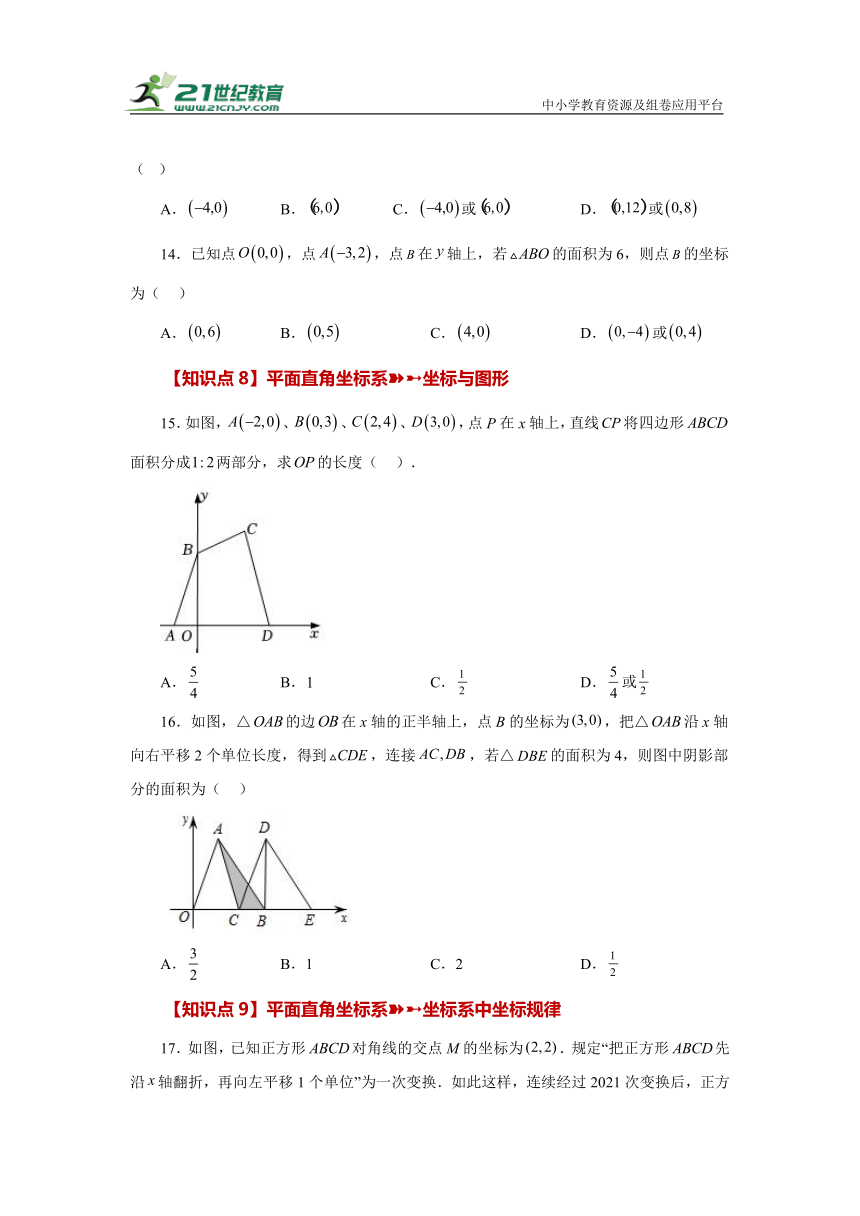
15.如图,、、、,点P在x轴上,直线将四边形面积分成两部分,求的长度( ).
A. B. C. D.或
16.如图,△的边在x轴的正半轴上,点B的坐标为,把△沿x轴向右平移2个单位长度,得到,连接,若△的面积为4,则图中阴影部分的面积为( )
A. B.1 C.2 D.
【知识点9】平面直角坐标系 坐标系中坐标规律
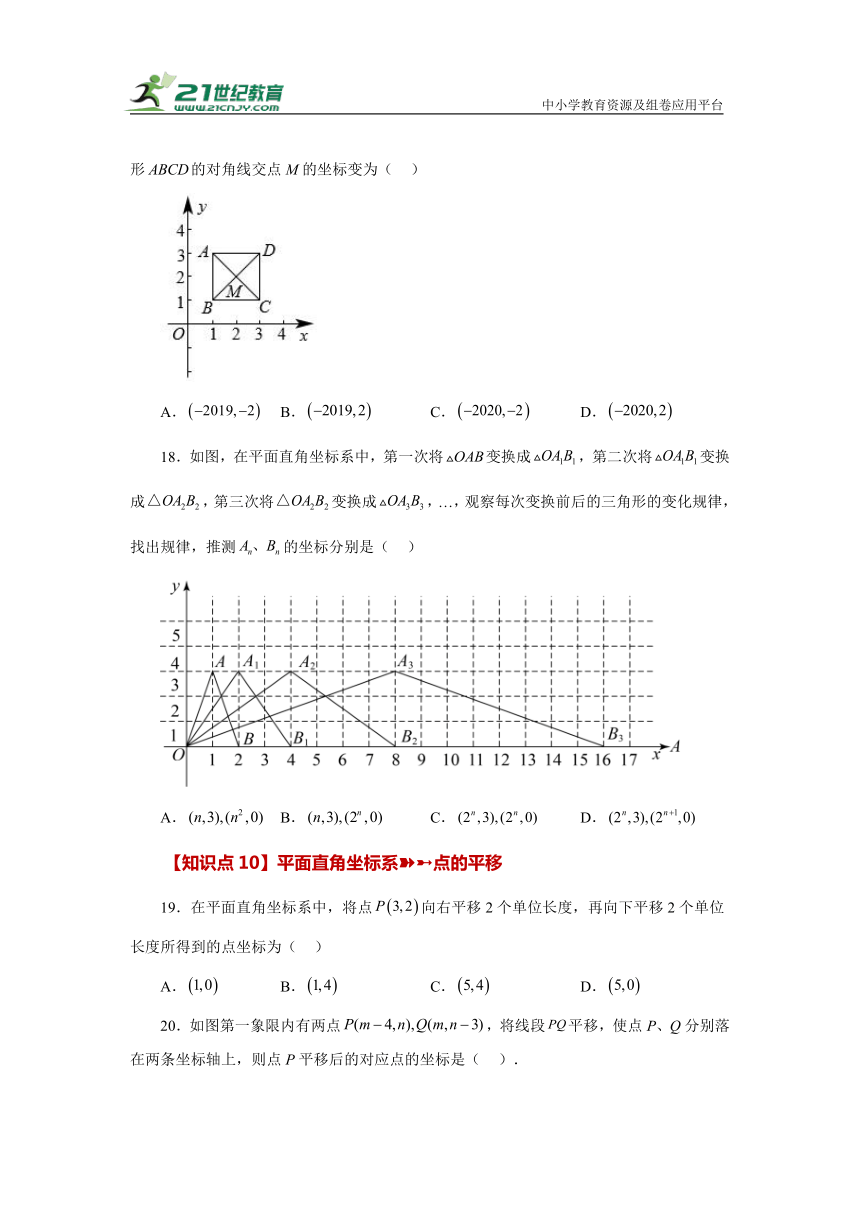
17.如图,已知正方形对角线的交点M的坐标为.规定“把正方形先沿轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2021次变换后,正方形的对角线交点M的坐标变为( )
A. B. C. D.
18.如图,在平面直角坐标系中,第一次将变换成,第二次将变换成,第三次将变换成,…,观察每次变换前后的三角形的变化规律,找出规律,推测的坐标分别是( )
A. B. C. D.
【知识点10】平面直角坐标系 点的平移
19.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
20.如图第一象限内有两点,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是( ).
A. B. C.或 D.或
【知识点11】平面直角坐标系 平移几何变换
21.如图,在三角形中,,,,,将三角形沿直线向右平移3个单位得到三角形,连接.则下列结论:
①,;
②;
③四边形的周长是18;
④;
⑤点到的距离为2.4.
其中正确结论的个数有( )
A.5 B.4 C.3 D.2
22.如图,在平面直角坐标系中,已知A(﹣2,0),B(5,0),C(0,3),平移线段AC至线段BD,点P在四边形OBDC内,满足S△PCD=S△PBD,S△POB:S△POC=5:6,则点P的坐标为( )
A.(2,1) B.(2,4) C.(3,2) D.(4,2)
二、填空题
【知识点1】有序数对
23.八年级某班有48名学生,所在教室有6行8列座位,用表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为,若调整后的座位为,则称该生作了平移,并称为该生的位置数.若某生的位置数为11,则当取最小值时,的最大值为_________.
24.如图,若“帅”位于点,“马”位于点,则“兵”位于点_______.
【知识点2】有序数对 规律问题 新定义
25.将自然数按图规律排列:如果一个数在第m行第n列,那么记它的位置为有序数对,例如:数2在第2行第1列,记它的位置为有序数对.按照这种方式,(1)位置为有序数对的数是______;(2)数位置为有序数对______.
26.将正整数按如图的规律排列,若用有序数对(m,n)表示从上到下第m行,和该行从左到右第n个数,如(4,2)表示整数8,则(6,3)表示的整数是_____________
【知识点3】平面直角坐标系 点的坐标 点到坐标轴距离
27.已知点,点,点是坐标轴上一动点,若三角形的面积为,则的坐标为__________.
28.已知点A(3a+6,a+4),B(﹣3,2),ABx轴,点P为直线AB上一点,且PA=2PB,则点P的坐标为_____________.
【知识点4】平面直角坐标系 点的坐标 点所在的位置
29.已知,则在平面直角坐标系中,点不可能出现在第___________象限.
30.若关于x的方程的解为负数,则点(m,m+2)在第____________象限.
【知识点5】平面直角坐标系 点所在的位置 求参数
31.点在坐标轴上,则点P的坐标为______.
32.在平面直角坐标系中,若点A(m2﹣4,m+1)在y轴的非负半轴上,则点B(m﹣1,1﹣2m)在第 ___象限.
【知识点6】平面直角坐标系 坐标系中描点
33.如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比纵坐标大2,对于∠xOy,满足d(P,∠xOy)=10,点P的坐标是_____.
34.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:________.
【知识点7】平面直角坐标系 坐标与面积
35.如果点,,点C在y轴上,且的面积是5,则C点坐标_________.
36.已知,,若点在轴上,且的面积为,则点的坐标为______.
【知识点8】平面直角坐标系 坐标与图形
37.在平面直角坐标系中,点与点(是任意实数)的距离的最小值为______.
38.如图,将正方形放在平面直角坐标系中,为坐标原点,点的坐标为,则点的坐标为______.
【知识点9】平面直角坐标系 坐标系中坐标规律
39.如图,矩形的两边分别在轴、轴上,点与原点重合,点,将矩形沿轴向右翻滚,经过一次翻滚点对应点记为,经过第二次翻滚点对应点记为…依此类推,经过次翻滚后点对应点记为的坐标为____.
40.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去….若点,,则点的坐标为_______.
【知识点10】平面直角坐标系 点的平移
41.如图,在平面直角坐标系中,三角形ABC经过平移后得到三角形A′B′C′,且平移前后三角形的顶点坐标都是整数.若点P(,﹣)为三角形ABC内部一点,且与三角形A′B′C′内部的点P′对应,则对应点P′的坐标是_____.
42.如图,在平面直角坐标系中,将四边形先向下平移,再向右平移,得到四边形,已知点,点,点,则点的坐标为___.
【知识点11】平面直角坐标系 平移几何变换
43.在平面直角坐标系xOy中,将A(a,b),B(m,b + 1)(a≠m + 1)两点同时向右平移h(h > 0)个单位,再向下平移1个单位得到C,D两点(点A对应点C).连接AD,过点B作AD的垂线l,E是直线l上一点,连接DE,且DE的最小值为1.下列结论正确的有 _________ .(只填序号)
①AC = BD;②直线l⊥x轴;③A、B、C三点可能在同一条直线上;④当DE取最小值时,点E的坐标为(m,b).(写出所有正确结论的序号)
44.如图,在中,,,.将沿射线的方向向右平移个单位后得到,连接,则的面积为______.
参考答案
1.C
【分析】根据坐标确定位置需要确定的有序数对,据此对各选项进行分析即可求解.
解:A、东经37°,北纬21°物体的位置明确,故本选项不符合题意;
B、电影院某放映厅7排3号物体的位置明确,故本选项不符合题意;
C、鹤壁淇滨大道无法确定物体的具体位置,故本选项符合题意;
D、外国语中学北偏东60°方向,距离为3千米物体的位置明确,故本选项不符合题意;
故选:C.
【点拨】本题考查了坐标确定位置,理解位置的确定需确定的有序数对是解答本题的关键.
2.B
【分析】由用有序数对表示点的平移,得到的数为1,得到的数为3,可得平移的方向:后一个数为正数表示向左平移,为负数表示向右平移,而平移的距离是后一个数的绝对值,从而可得答案.
解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
【点拨】本题考查的是有序实数对表示平移,正确的理解平移的方向与平移的距离是解题的关键.
3.B
【分析】根据有序数对(m,n)表示第m行从左到右第n个数,对如图中给出的有序数对和(3,2)表示整数5可得规律,进而可求出(9,4)表示的数.
解:根据有序数对(m,n)表示第m行从左到右第n个数,
对如图中给出的有序数对和(3,2)表示整数5可知:
(3,2):;
(3,1):;
(4,4):;
…
由此可以发现,对所有数对(m,n)(n≤m)有,.
表示的数是偶数时结果为负数,奇数时结果为正数,
所以(9,4)表示的数是:.
故选:B.
【点拨】本题考查了规律型-图形的变化类,解决本题的关键是观察数字的变化寻找规律,总结规律.
4.C
【分析】不难发现横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,根据此规律即可知第50个有序数对.
解:观察发现,横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,
,
第46、47、48、49、50个有序数对依次是、、、、.
所以C选项是正确的.
【点拨】本题主要考查了点的坐标探索规律题,找出有序数对的横、纵坐标变化规律是解决问题的关键.
5.A
【分析】根据关于直线x=1对称,则纵坐标相等,横坐标关于直线x=1对称,进而得出答案.
解:∵点M(-2,1)与N点关于直线x=1成轴对称,
∴M点与N点纵坐标相等,横坐标到直线x=1的距离相等,
∴点N的坐标是(4,1).
故选:A.
【点拨】此题主要考查了点的坐标性质,根据已知得出两点坐标性质是解题关键.
6.A
【分析】根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故选:A.
【点拨】本题考查已知点求坐标及如何根据坐标描点,正确画图即可求解.
7.D
【分析】直接利用点在第一象限得出ab>0,a≠0,即可得出点B所在象限.
解:∵点在第一象限,
∴>0,
∴ab>0,a≠0,
∴-a2<0,
则点在第四象限.
故选:D.
【点拨】此题主要考查了点的坐标,正确得出横纵坐标的符号是解题关键.
8.C
【分析】应用坐标与图形性质进行判定即可得出答案.
解:A.因为当时,点在轴上,所以A选项说法不一定正确,故A选项不符合题意;
B.因为当,,或,时,,则在轴或轴上,不一定在坐标原点,所以B选项说法不一定正确,故B选项不符合题意;
C.因为点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为,所以C选项说法正确,故C选项符合题意;
D.因为在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为或,所以D选项说法不正确,故D选项不符合题意.
故选:C.
【点拨】本题主要考查了坐标与图形性质,熟练掌握坐标与图形性质进行求解是解决本题的关键.
9.B
【分析】先根据点A在y轴上求出m,从而可得,结合数轴可知当当CP⊥x轴时,CP长度最小,求出点P的坐标即可.
解:∵点在y轴上,
∴m-1=0
解得m=1,
∴
如图所示,∵点P是直线AB上的动点,
∴当CP⊥x轴时,CP长度最小,
∴点P(4,3).
故选:B.
【点拨】本题考查坐标轴上点的坐标特征,垂线段最短等知识点,解题关键是理解x轴上点的纵坐标为0,y轴上点的横坐标为0.
10.C
【分析】根据x轴上点的纵坐标为0列方程求解即可.
解:∵点P(3m+3,2m-2)在x轴上,
∴2m-2=0,
解得m=1.
故选:C.
【点拨】本题考查了点的坐标,熟记x轴上点的纵坐标为0是解题的关键.
11.C
【分析】A(3,2),B(2,3),横纵坐标不相等,故不为同一个点,也不能够重合.
解:根据题意, A(3,2), B(2,3),
由于A、B两点的横纵坐标不相等,
故A、B两点不为同一个点,即不能够重合.
所以C选项是正确的.
【点拨】本题考查的是点的坐标的基本知识,理解概念是解题关键.
12.C
解:试题分析:根据|x|=5可得x=±5,|x﹣y|=8可得y的值,组合即为点P的坐标.
解:∵|x|=5,
∴x=±5;
∵|x﹣y|=8,
∴x﹣y=±8,
∴y=±3,y=±13,
∴点P的坐标为(5,3);(5,﹣3);(5,13);(5,﹣13);(﹣5,3);(﹣5,﹣3);(﹣5,13)(﹣5,﹣13)共8个,
∵x﹣y=±8,
∴(5,3);(5,﹣13);(﹣5,﹣3);(﹣5,13)不符合题意,故有4个符合题意.
故选C.
点评:用到的知识点为:绝对值为正数的数有2个;注意找到合适的坐标.
13.C
【分析】根据B点的坐标可知边上的高为2,而的面积为5,点P在x轴上,可得,设点P的坐标为,再根据数轴上两点间的距离,即可求得P点坐标.
解:,,点P在x轴上,
的边上的高为2,
又的面积为5,
,
设点P的坐标为,
则,
或,
解得或,
点P的坐标为或,
故选:C.
【点拨】本题考查三角形的面积,坐标与图形的性质等知识,解题的关键是学会利用参数构建方程解决问题.
14.D
【分析】分情况考虑,首先当B在y轴的正半轴上时,根据图形可知, 以为底,则高是点A的横坐标的绝对值,根据面积为6,可求出的长,即求出B点的坐标,再由点B在y轴,确定点B的坐标.
解:如图当B在y轴的正半轴上时,
∵的面积为6,
∴,
∵点B在y轴上,
则点B的坐标为或.
故选:D.
【点拨】本题考查平面直角坐标系,将点的坐标转化为线段的长,是解决问题的关键.
15.B
【分析】用分割法求出四边形的面积,分类讨论求出的面积,再求出的值,进而可得的值.
解:作轴于点P,
∵、、、,
∴,
∴,
,
,
,
∴,
∴,
①当即时,
即,解得:,
∴;
②当即时,
即,解得:,
∴;
综上可知.
故选:B.
【点拨】本题考查了坐标与图形的性质,三角形的面积,根据坐标与图形的性质,用分割法求出不规则图形的面积,分类讨论是解本题的关键.
16.C
【分析】设A(m,n),由B(3,0)可知OB=3,由平移的性质可得CE=OB=3,BE=OC=2,由三角形面积公式可求出n,即可求出求出阴影部分的面积.
解:设A(m,n)
∵B(3,0),
∴OB=3.
由平移的性质可得
CE=OB=3,BE=OC=2,
∴CB=CE-BE=1.
∵S△DBE==4,
∴,
∴n=4,
∴S阴影=S△ACB==.
故选:C
【点拨】本题主要考查了坐标系中的平移变换.掌握平移的性质并能求出n的值是解题的关键.
17.A
【分析】根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为,当n为偶数时为,继而求得把正方形连续经过2021次这样的变换得到正方形的对角线交点M的坐标.
解:∵对角线交点M的坐标为,
根据题意得:第1次变换后的点M的对应点的坐标为,即,
第2次变换后的点M的对应点的坐标为:,即,
第3次变换后的点M的对应点的坐标为,即,
第n次变换后的点M的对应点的为:当n为奇数时为,当n为偶数时为,
∴连续经过2021次变换后,正方形的对角线交点M的坐标变为.
故选:A.
【点拨】此题考查了点的坐标变化,对称与平移的性质,得到规律:第n次变换后的对角线交点M的对应点的坐标为:当n为奇数时为,当n为偶数时为是解此题的关键.
18.D
【分析】根据图中各点的坐标的变化,依次写出,.再根据点的坐标变化的特点写出的坐标即可.
解:,
;
,
;
故选:D.
【点拨】此题考查了坐标与图形的变化,正确写出前几个点的坐标、找出坐标变化的规律是解答此题的关键.
19.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点拨】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
20.C
【分析】设平移后点、的对应点分别是、.分两种情况进行讨论:①在轴上,在轴上;②在轴上,在轴上.
解:设平移后点、的对应点分别是、.
分两种情况:
①在轴上,在轴上,
则横坐标为0,纵坐标为0,
,
,
点平移后的对应点的坐标是;
②在轴上,在轴上,
则纵坐标为0,横坐标为0,
,
,
点平移后的对应点的坐标是;
综上可知,点平移后的对应点的坐标是或.
故选:C.
【点拨】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
21.A
【分析】设AC与DE的交点为H,根据平移的性质可得,然后可得,过点A作AG⊥BC于点G,则AG即为点A到BC的距离,然后利用等积法可进行求解.
解:设AC与DE的交点为H,如图所示:
∵,将三角形沿直线向右平移3个单位得到三角形,连接,
∴根据平移的性质知,,故①正确;
∵,
∴,故②正确;
∵,,
∴四边形的周长为
,故③正确;
∵,
∴,故④正确;
过点A作AG⊥BC于点G,则AG即为点A到BC的距离,如图,
∵,
∴,故⑤正确;
∴正确的个数有5个;
故选A.
【点拨】本题主要考查平移的性质及平行线的性质与判定,熟练掌握平移的性质是解题的关键.
22.D
【分析】过P作PM⊥OB于M,并反向延长交CD于N,设P(x,y),根据S△POB:S△POC=5:6,于是得到x=2y;由于S△PCD=S△PBD,于是得到×7 (3-y)=18-×7(3-y)-×3x-×5y,最后解方程组即可得到结论.
解:如图,过P作PM⊥OB于M,交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(x,y),
∵S△POB:S△POC=5:6,
∴5××3x=6××5y,
∴x=2y,①
∵S△PCD=S△PBD,
∴×7 (3﹣y)=18﹣×7(3﹣y)﹣×3x﹣×5y,②
由①、②解得x=4,y=2,
∴P(4,2),
故选:D.
【点拨】本题主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,作辅助线构造平行线和垂线是解题的关键.
23.42
【分析】求出m+n取最小值时,m、n的关系式,又,2,3,4,5,6,计算的值,比较求出最大的值.
解:由题意得,
则,
∵,,且i、j都是整数,
∴当时,取最小值13,
此时,
∴,
又,2,3,4,5,6.
则时,;m=2时,;时,;时,;时,;时,.
则的最大值是42.
故答案为:42.
【点拨】本题考查了利用坐标表示位置,几何变换的代数表示法,属于新定义型题目,解答本题需要同学们仔细审题,理解位置数是怎样规定的.
24.(-2,2)
【分析】根据“帅”和“马”的位置,可确定原点O的位置,即可得答案.
解:如下图,
∵“帅”位于点(0, 1),“马”位于点(3, 1),
∴原点O的位置如上图,
∴“兵”位于点(-2,2),
故答案为:(-2,2).
【点拨】本题考查了平面上物体位置的确定,解题的关键是确定原点O的位置.
25. (9,6)
【分析】根据题意,找出题目的规律,中含有4个数,中含有9个数,中含有16个数,……,中含有64个数,且奇数行都是从左边第一个数开始,然后根据这个规律即可得出答案.
解:根据题意,如图:
∴有序数对的数是;
由图可知,中含有4个数,中含有9个数,中含有16个数;
……
∴中含有64个数,且奇数行都是从左边第一个数开始,
∵,
∴是第九行的第6个数;
∴数位置为有序数对是(9,6).
故答案为:;(9,6).
【点拨】此题考查数字的变化规律,找出数字之间的联系,得出运算规律,解决问题.
26.18.
【分析】(m,n)的规律是m表示从上到下第m行又表示第m行有m个数,n表示该行从左到右第n个数,(1,1)第一行1个数是1,(2,2)表示的数是1+2=3,(3,3)表示的数是1+2+3=6,
…以此类推(m-1,m-1)表示的数是1+2+3+…+m-1=,为此(m,n)表示的数是+n,当m=4,n=2表示的数为×4×3+2=6+2=8,为此(6,3)只要求代数式的即可.
解:先计算前m-1行最后一个数为:1+2+3+…+m-1=,
再求(m,n)表示的数,第m行从左到右第n个数,即为+n,
当m=6,n=3,代入+n=×6×5+3=18,
(6,3)表示的整数是18.
故答案为:18.
【点拨】本题考查数字规律探索问题,关键用数形结合思想,发相规律,用代数式表示规律,用规律解决问题.
27.或,或
【分析】首先根据条件画出图,如图所示,当点在轴上时,则为底,点的纵坐标数值为高,根据面积公式求出底的长度,即可得到点坐标;当点在轴上时,可分析出不可能在正半轴,故只能在负半轴,如图,设出点坐标,用割补法表示的面积即可求得.
解:当点在轴上时,
解得:
所以点有两个,,
当点在轴上时,
点符合题意,当点向上移动时,面积变大,
在正半轴不存在符合条件的点.
设在轴负半轴上点,
则
即:
解得:
所以,点坐标为
故答案为:或或
【点拨】本题主要考查了分类讨论的数学思想,相关知识点有:割补法求面积,对点的位置进行分类讨论是解题的关键.
28.或##或
【分析】根据ABx轴,则的纵坐标相等,求得的值,进而确定的坐标,根据即可求解.
解:∵A(3a+6,a+4),B(﹣3,2),ABx轴,
∴,
解得,
∴,
∴,
设,
①当在的延长线上时,,
,
解得,
∴,
②当在线段上时,,
,
解得,
∴,
③当在的延长线上时,,不符合题意,
综上所述,点的坐标为或,
故答案为:或.
【点拨】本题考查了坐标与图形,数形结合求得点的坐标是解题的关键.
29.第二象限
【分析】根据得到分计算即可.
解:∵,
∴,
当时,
得,
此时经过第一象限;
当时,
得,
此时经过第四象限;
当时,
得,
此时经过第三象限;
故不经过第二象限.
故答案为:第二象限.
【点拨】本题考查了坐标与象限,正确分类是计算判断的关键.
30.三
【分析】把m看作常数,根据一元一次方程的解法求出x的表达式,再根据方程的解是负数列不等式并求解即可.
解:由,得
x=2+m.
∵关于x的方程的解是负数,
∴2+m<0,
解得m<-2
∴(m,m+2)在第三象限
故答案是:三.
【点拨】本题考查了一元一次方程的解与解不等式,把m看作常数求出x的表达式是解题的关键.
31.或
【分析】分点P在轴和轴上两种情况,进行讨论求解即可.
解:当点P在轴上时:,解得:,
∴,
∴;
当点P在轴上时:,解得:,
∴,
∴;
综上:点P的坐标为:或;
故答案为:或.
【点拨】本题考查坐标轴上点的特征.熟练掌握坐标轴上的点的横坐标或纵坐标为0,是解题的关键.
32.四
【分析】根据点A(m2﹣4,m+1)在y轴的非负半轴上可得,据此求出m的值,再根据各象限内点的坐标的符号进行判断即可.
解:∵点A(m2﹣4,m+1)在y轴的非负半轴上,
∴,
解得m=2,
∴m﹣1=1,1﹣2m=﹣3,
∵(1,﹣3)在第四象限,
∴点B(m﹣1,1﹣2m)在第四象限.
故答案为:四.
【点拨】本题主要考查了平面直角坐标系象限内点的坐标特征,准确计算是解题的关键.
33.(6,4)或(﹣4,﹣6)
【分析】设点P的横坐标为x,表示出纵坐标,然后列方程求出x,再求解即可.
解:设点P的横坐标为x,则点P的纵坐标为x-2,由题意得,
当点P在第一象限时,x+x-2=10,
解得x=6,
∴x-2=4,
∴P(6,4);
当点P在第三象限时,-x-x+2=10,
解得x=-4,
∴x-2=-6,
∴P(-4,-6).
故答案为(6,4)或(-4,-6).
【点拨】本题主要考查了点的坐标,读懂题目信息,理解“点角距离”的定义并列出方程是解题的关键.
34.(-5,0),(5,0),(0,4),(0,-4)
【分析】根据题意可知点C在x轴上或者在y轴上,通过分析,根据AC+BC=10,符合要求的有四种情况,可以确定点C的坐标.
解:第一种情况:当点C在x轴左半轴时,点C在点A的左侧.
若C在点A的右侧,只能当A与C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).
∵AC+BC=10,点A(-3,0),B(3,0),
∴(-3-x)+(3-x)=10.
解得,x=-5.
∴点C的坐标为(-5,0),点A(-3,0),B(3,0),
第二种情况:当点C在x轴左半轴时,点C在点B的右侧.
若C在点B的左侧,只能当与B,C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).
∵AC+BC=10,
∴[x-(-3)]+(x-3)=10.
解得,x=5.
∴点C的坐标为(5,0).
第三种情况:点C在y轴上方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y =52.
解得,y=±4.
∵点C在y轴上方,
∴点C的坐标为(0,4).
第四种情况:点C在y轴下方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y =52.
解得,y=±4.
∵点C在y轴下方,
∴点C的坐标为(0,-4).
故答案为(-5,0),(5,0),(0,4),(0,-4).
【点拨】本题考查的是坐标与图形的性质,熟练掌握图形与坐标的性质是解题的关键.
35.或
【分析】设点C的坐标为,求出的长,再根据三角形的面积公式列式计算即可.
解:设点C的坐标为,
∵,,
∴,
由题意得:,解得:或,
∴点C的坐标为或.
故答案为:或.
【点拨】本题主要考查的是三角形的面积、坐标与图形性质等知识点,正确表示出的长、灵活运用三角形的面积公式是解题的关键.
36.或
【分析】先画出图形,设点的坐标为,则,,再利用三角形的面积公式建立方程,解方程即可得.
解:由题意,画出图形如下:
设点的坐标为,
,,
,,
又的面积为,且轴轴,
,
解得或,
故点的坐标为或,
故答案为:或.
【点拨】本题考查了坐标与图形,利用三角形的面积公式正确建立方程是解题关键.
37.4
【分析】根据可知:点A在直线上,根据垂线段最短,可知:当点A与点B的连线与直线垂直时,线段最短,据此即可作答.
解:根据可知:点A在直线上,
根据垂线段最短,可知:当点A与点B的连线与直线垂直时,线段最短,
∵与直线垂直,直线与x轴平行,
∴轴,
∴点A与点B的横坐标相等,
∴,
即点A与点B的最小距离为4,
故答案为:4.
【点拨】本题考查了坐标系中两点之间的距离以及垂线段最短的知识,掌握垂线段最短是解答本题的关键.
38.
【分析】过点作轴于,过点作交的延长线于点,设交轴于点,证明,求出,即可解得.
解:如图,过点作轴于,过点作交的延长线于点,设交轴于点,
,
四边形为正方形,
,,
,
又,
,
≌,
,,
点的坐标为,
,,
,,
,
故答案为:.
【点拨】本题考查的是图形与坐标,正方形的性质,三角形全等的判定与性质,掌握利用垂直证明三角形全等是解题的关键.
39.
【分析】根据题意,确定图形从开始位置经过4次翻滚后点进行了一次循环回到对应位置,从而结合长方形周长为,依据即可得到答案.
解:如图所示:
,
观察图形可知,经过4次翻滚后点进行了一次循环回到对应位置,,
∵长方形的周长为:,
每一次完整循环,相当于对应点的横坐标,纵坐标保持不变,
,即经过了次完整的循环后再向前翻滚次,是的对应点,
∴经过次翻滚后点对应点的坐标为,即,
故答案为:.
【点拨】本题考查动点坐标规律,读懂题意,理解图形从开始位置经过4次翻滚后点进行了一次循环回到对应位置是解决问题的关键.
40.
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、、…每偶数之间的B相差6个单位长度,根据这个规律可以求得的坐标.
解:∵点,,
∴,,
∴,
∴,
∴的横坐标为:6,且,点的纵坐标为:2
∴的横坐标为:,点的纵坐标为:2
∴点的横坐标为:.
∴点的纵坐标为:2.
故点的坐标为.
故答案为:.
【点拨】本题考查点的坐标规律变换,解题关键是通过图形旋转,找到所有B点之间的关系.
41.(,)
【分析】依据对应点的坐标变化,即可得到三角形ABC向左平移2个单位,向上平移3个单位后得到三角形A′B′C′,进而得出点P′的坐标.
解:由图可得,C(2,0),C'(0,3),
∴三角形ABC向左平移2个单位,向上平移3个单位后得到三角形A′B′C′,
又∵点P(,﹣)为三角形ABC内部一点,且与三角形A′B′C′内部的点P′对应,
∴对应点P′的坐标为(﹣2,﹣+3),即P'(,),
故答案为:(,).
【点拨】此题主要考查了坐标与图形变化,关键是注意观察组成图形的关键点平移后的位置.解题时注意:横坐标,右移加,左移减;纵坐标,上移加,下移减.
42.(2,1)
【分析】根据A和A1的坐标得出四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,则B的平移方法与A点相同,即可得到答案.
解:由A(-3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(-4,3),
∴B1的坐标为(2,1),
故答案为:(2,1).
【点拨】此题主要考查了点的平移规律与图形的平移,关键是掌握平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减.
43.①②④
【分析】根据平移的性质先求出点C和点D的坐标,得到点A和点D的纵坐标相同,进而得到轴,再利用平移的性质来求解.
解:∵A(a,b),B(m,b + 1)(a≠m + 1)两点同时向右平移h(h > 0)个单位,再向下平移1个单位得到C,D两点(点A对应点C),
一个点向右平移h个单位,则该点的横坐标加h;一个点向下平移1个单位,则该点的纵坐标减1,
∴,,
此时点A和点D的纵坐标相同,
∴轴.
根据平移的性质可知:,故①正确;
AD平行于x轴,l垂直于AD
那么l也垂直于x轴,故②正确;
由图可知:因为a≠m + 1,所以A、B、C三点不可能在同一条直线上,故③错误;
当DE取最小值时,点E与点P重合时,
此时点E的坐标为(m,b),故④正确.
综上所述,正确的有:①②④.
【点拨】本题主要考查了平移的性质,理解平移的性质和求出平移后点C和D的坐标是解答关键.
44.
【分析】根据平移的性质,可得答案.
解:过点作,如图,
,
,,
,
的面积,
平移不改变图形的形状和大小,
△的面积为,
故答案为:
中小学教育资源及组卷应用平台
【点拨】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
(巩固篇)(专项练习)
一、单选题
【知识点1】有序数对
1.下列在具体情境中不能确定平面内位置的是( )
A.东经37°,北纬21° B.电影院某放映厅7排3号
C.鹤壁淇滨大道 D.外国语中学北偏东60°方向,2千米处
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
【知识点2】有序数对 规律问题 新定义
3.如图,将整数按规律排列,若有序数对(a,b)表示第a排从左往右第b个数,则(9,4)表示的数是( )
A.49 B.﹣40 C.﹣32 D.25
4.观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
A.(3,8) B.(4,7) C.(5,6) D.(6,5)
【知识点3】平面直角坐标系 点的坐标 点到坐标轴距离
5.已知点与点关于直线成轴对称,则点的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10, C.1, D.6,
【知识点4】平面直角坐标系 点的坐标 点所在的位置
7.若点在第一象限,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列说法正确的是( )
A.点在第四象限
B.若,则在坐标原点
C.点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为
D.在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为
【知识点5】平面直角坐标系 点所在的位置 求参数
9.在平面直角坐标系中,有三点,其中点A落在y轴上,P为直线AB上的一动点,若PC连线的长度最短,此时点P的坐标为( )
A. B. C. D.
10.在平面直角坐标系中,点在x轴上,则m的值为( )
A. B. C.1 D.3
【知识点6】平面直角坐标系 坐标系中描点
11.若有点A和点B,坐标分别为A(3,2),B(2,3),则( )
A.A,B为同一个点 B.A,B为重合的两点
C.A,B为不重合的两点 D.无法确定
12.在直角坐标系中,适合条件|x|=5,|x﹣y|=8的点P(x,y)的个数为( )
A.1 B.2 C.4 D.8
【知识点7】平面直角坐标系 坐标与面积
13.已知点,,点P在x轴上,且的面积为5,则点P的坐标是( )
A. B. C.或 D.或
14.已知点,点,点在轴上,若的面积为6,则点的坐标为( )
A. B. C. D.或
【知识点8】平面直角坐标系 坐标与图形
15.如图,、、、,点P在x轴上,直线将四边形面积分成两部分,求的长度( ).
A. B. C. D.或
16.如图,△的边在x轴的正半轴上,点B的坐标为,把△沿x轴向右平移2个单位长度,得到,连接,若△的面积为4,则图中阴影部分的面积为( )
A. B.1 C.2 D.
【知识点9】平面直角坐标系 坐标系中坐标规律
17.如图,已知正方形对角线的交点M的坐标为.规定“把正方形先沿轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2021次变换后,正方形的对角线交点M的坐标变为( )
A. B. C. D.
18.如图,在平面直角坐标系中,第一次将变换成,第二次将变换成,第三次将变换成,…,观察每次变换前后的三角形的变化规律,找出规律,推测的坐标分别是( )
A. B. C. D.
【知识点10】平面直角坐标系 点的平移
19.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
20.如图第一象限内有两点,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是( ).
A. B. C.或 D.或
【知识点11】平面直角坐标系 平移几何变换
21.如图,在三角形中,,,,,将三角形沿直线向右平移3个单位得到三角形,连接.则下列结论:
①,;
②;
③四边形的周长是18;
④;
⑤点到的距离为2.4.
其中正确结论的个数有( )
A.5 B.4 C.3 D.2
22.如图,在平面直角坐标系中,已知A(﹣2,0),B(5,0),C(0,3),平移线段AC至线段BD,点P在四边形OBDC内,满足S△PCD=S△PBD,S△POB:S△POC=5:6,则点P的坐标为( )
A.(2,1) B.(2,4) C.(3,2) D.(4,2)
二、填空题
【知识点1】有序数对
23.八年级某班有48名学生,所在教室有6行8列座位,用表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为,若调整后的座位为,则称该生作了平移,并称为该生的位置数.若某生的位置数为11,则当取最小值时,的最大值为_________.
24.如图,若“帅”位于点,“马”位于点,则“兵”位于点_______.
【知识点2】有序数对 规律问题 新定义
25.将自然数按图规律排列:如果一个数在第m行第n列,那么记它的位置为有序数对,例如:数2在第2行第1列,记它的位置为有序数对.按照这种方式,(1)位置为有序数对的数是______;(2)数位置为有序数对______.
26.将正整数按如图的规律排列,若用有序数对(m,n)表示从上到下第m行,和该行从左到右第n个数,如(4,2)表示整数8,则(6,3)表示的整数是_____________
【知识点3】平面直角坐标系 点的坐标 点到坐标轴距离
27.已知点,点,点是坐标轴上一动点,若三角形的面积为,则的坐标为__________.
28.已知点A(3a+6,a+4),B(﹣3,2),ABx轴,点P为直线AB上一点,且PA=2PB,则点P的坐标为_____________.
【知识点4】平面直角坐标系 点的坐标 点所在的位置
29.已知,则在平面直角坐标系中,点不可能出现在第___________象限.
30.若关于x的方程的解为负数,则点(m,m+2)在第____________象限.
【知识点5】平面直角坐标系 点所在的位置 求参数
31.点在坐标轴上,则点P的坐标为______.
32.在平面直角坐标系中,若点A(m2﹣4,m+1)在y轴的非负半轴上,则点B(m﹣1,1﹣2m)在第 ___象限.
【知识点6】平面直角坐标系 坐标系中描点
33.如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比纵坐标大2,对于∠xOy,满足d(P,∠xOy)=10,点P的坐标是_____.
34.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:________.
【知识点7】平面直角坐标系 坐标与面积
35.如果点,,点C在y轴上,且的面积是5,则C点坐标_________.
36.已知,,若点在轴上,且的面积为,则点的坐标为______.
【知识点8】平面直角坐标系 坐标与图形
37.在平面直角坐标系中,点与点(是任意实数)的距离的最小值为______.
38.如图,将正方形放在平面直角坐标系中,为坐标原点,点的坐标为,则点的坐标为______.
【知识点9】平面直角坐标系 坐标系中坐标规律
39.如图,矩形的两边分别在轴、轴上,点与原点重合,点,将矩形沿轴向右翻滚,经过一次翻滚点对应点记为,经过第二次翻滚点对应点记为…依此类推,经过次翻滚后点对应点记为的坐标为____.
40.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去….若点,,则点的坐标为_______.
【知识点10】平面直角坐标系 点的平移
41.如图,在平面直角坐标系中,三角形ABC经过平移后得到三角形A′B′C′,且平移前后三角形的顶点坐标都是整数.若点P(,﹣)为三角形ABC内部一点,且与三角形A′B′C′内部的点P′对应,则对应点P′的坐标是_____.
42.如图,在平面直角坐标系中,将四边形先向下平移,再向右平移,得到四边形,已知点,点,点,则点的坐标为___.
【知识点11】平面直角坐标系 平移几何变换
43.在平面直角坐标系xOy中,将A(a,b),B(m,b + 1)(a≠m + 1)两点同时向右平移h(h > 0)个单位,再向下平移1个单位得到C,D两点(点A对应点C).连接AD,过点B作AD的垂线l,E是直线l上一点,连接DE,且DE的最小值为1.下列结论正确的有 _________ .(只填序号)
①AC = BD;②直线l⊥x轴;③A、B、C三点可能在同一条直线上;④当DE取最小值时,点E的坐标为(m,b).(写出所有正确结论的序号)
44.如图,在中,,,.将沿射线的方向向右平移个单位后得到,连接,则的面积为______.
参考答案
1.C
【分析】根据坐标确定位置需要确定的有序数对,据此对各选项进行分析即可求解.
解:A、东经37°,北纬21°物体的位置明确,故本选项不符合题意;
B、电影院某放映厅7排3号物体的位置明确,故本选项不符合题意;
C、鹤壁淇滨大道无法确定物体的具体位置,故本选项符合题意;
D、外国语中学北偏东60°方向,距离为3千米物体的位置明确,故本选项不符合题意;
故选:C.
【点拨】本题考查了坐标确定位置,理解位置的确定需确定的有序数对是解答本题的关键.
2.B
【分析】由用有序数对表示点的平移,得到的数为1,得到的数为3,可得平移的方向:后一个数为正数表示向左平移,为负数表示向右平移,而平移的距离是后一个数的绝对值,从而可得答案.
解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
【点拨】本题考查的是有序实数对表示平移,正确的理解平移的方向与平移的距离是解题的关键.
3.B
【分析】根据有序数对(m,n)表示第m行从左到右第n个数,对如图中给出的有序数对和(3,2)表示整数5可得规律,进而可求出(9,4)表示的数.
解:根据有序数对(m,n)表示第m行从左到右第n个数,
对如图中给出的有序数对和(3,2)表示整数5可知:
(3,2):;
(3,1):;
(4,4):;
…
由此可以发现,对所有数对(m,n)(n≤m)有,.
表示的数是偶数时结果为负数,奇数时结果为正数,
所以(9,4)表示的数是:.
故选:B.
【点拨】本题考查了规律型-图形的变化类,解决本题的关键是观察数字的变化寻找规律,总结规律.
4.C
【分析】不难发现横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,根据此规律即可知第50个有序数对.
解:观察发现,横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,
,
第46、47、48、49、50个有序数对依次是、、、、.
所以C选项是正确的.
【点拨】本题主要考查了点的坐标探索规律题,找出有序数对的横、纵坐标变化规律是解决问题的关键.
5.A
【分析】根据关于直线x=1对称,则纵坐标相等,横坐标关于直线x=1对称,进而得出答案.
解:∵点M(-2,1)与N点关于直线x=1成轴对称,
∴M点与N点纵坐标相等,横坐标到直线x=1的距离相等,
∴点N的坐标是(4,1).
故选:A.
【点拨】此题主要考查了点的坐标性质,根据已知得出两点坐标性质是解题关键.
6.A
【分析】根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故选:A.
【点拨】本题考查已知点求坐标及如何根据坐标描点,正确画图即可求解.
7.D
【分析】直接利用点在第一象限得出ab>0,a≠0,即可得出点B所在象限.
解:∵点在第一象限,
∴>0,
∴ab>0,a≠0,
∴-a2<0,
则点在第四象限.
故选:D.
【点拨】此题主要考查了点的坐标,正确得出横纵坐标的符号是解题关键.
8.C
【分析】应用坐标与图形性质进行判定即可得出答案.
解:A.因为当时,点在轴上,所以A选项说法不一定正确,故A选项不符合题意;
B.因为当,,或,时,,则在轴或轴上,不一定在坐标原点,所以B选项说法不一定正确,故B选项不符合题意;
C.因为点在第二象限,且点到轴的距离为,点到轴的距离为,则点的坐标为,所以C选项说法正确,故C选项符合题意;
D.因为在平面直角坐标系中,若点的坐标为,且平行于轴,,则点的坐标为或,所以D选项说法不正确,故D选项不符合题意.
故选:C.
【点拨】本题主要考查了坐标与图形性质,熟练掌握坐标与图形性质进行求解是解决本题的关键.
9.B
【分析】先根据点A在y轴上求出m,从而可得,结合数轴可知当当CP⊥x轴时,CP长度最小,求出点P的坐标即可.
解:∵点在y轴上,
∴m-1=0
解得m=1,
∴
如图所示,∵点P是直线AB上的动点,
∴当CP⊥x轴时,CP长度最小,
∴点P(4,3).
故选:B.
【点拨】本题考查坐标轴上点的坐标特征,垂线段最短等知识点,解题关键是理解x轴上点的纵坐标为0,y轴上点的横坐标为0.
10.C
【分析】根据x轴上点的纵坐标为0列方程求解即可.
解:∵点P(3m+3,2m-2)在x轴上,
∴2m-2=0,
解得m=1.
故选:C.
【点拨】本题考查了点的坐标,熟记x轴上点的纵坐标为0是解题的关键.
11.C
【分析】A(3,2),B(2,3),横纵坐标不相等,故不为同一个点,也不能够重合.
解:根据题意, A(3,2), B(2,3),
由于A、B两点的横纵坐标不相等,
故A、B两点不为同一个点,即不能够重合.
所以C选项是正确的.
【点拨】本题考查的是点的坐标的基本知识,理解概念是解题关键.
12.C
解:试题分析:根据|x|=5可得x=±5,|x﹣y|=8可得y的值,组合即为点P的坐标.
解:∵|x|=5,
∴x=±5;
∵|x﹣y|=8,
∴x﹣y=±8,
∴y=±3,y=±13,
∴点P的坐标为(5,3);(5,﹣3);(5,13);(5,﹣13);(﹣5,3);(﹣5,﹣3);(﹣5,13)(﹣5,﹣13)共8个,
∵x﹣y=±8,
∴(5,3);(5,﹣13);(﹣5,﹣3);(﹣5,13)不符合题意,故有4个符合题意.
故选C.
点评:用到的知识点为:绝对值为正数的数有2个;注意找到合适的坐标.
13.C
【分析】根据B点的坐标可知边上的高为2,而的面积为5,点P在x轴上,可得,设点P的坐标为,再根据数轴上两点间的距离,即可求得P点坐标.
解:,,点P在x轴上,
的边上的高为2,
又的面积为5,
,
设点P的坐标为,
则,
或,
解得或,
点P的坐标为或,
故选:C.
【点拨】本题考查三角形的面积,坐标与图形的性质等知识,解题的关键是学会利用参数构建方程解决问题.
14.D
【分析】分情况考虑,首先当B在y轴的正半轴上时,根据图形可知, 以为底,则高是点A的横坐标的绝对值,根据面积为6,可求出的长,即求出B点的坐标,再由点B在y轴,确定点B的坐标.
解:如图当B在y轴的正半轴上时,
∵的面积为6,
∴,
∵点B在y轴上,
则点B的坐标为或.
故选:D.
【点拨】本题考查平面直角坐标系,将点的坐标转化为线段的长,是解决问题的关键.
15.B
【分析】用分割法求出四边形的面积,分类讨论求出的面积,再求出的值,进而可得的值.
解:作轴于点P,
∵、、、,
∴,
∴,
,
,
,
∴,
∴,
①当即时,
即,解得:,
∴;
②当即时,
即,解得:,
∴;
综上可知.
故选:B.
【点拨】本题考查了坐标与图形的性质,三角形的面积,根据坐标与图形的性质,用分割法求出不规则图形的面积,分类讨论是解本题的关键.
16.C
【分析】设A(m,n),由B(3,0)可知OB=3,由平移的性质可得CE=OB=3,BE=OC=2,由三角形面积公式可求出n,即可求出求出阴影部分的面积.
解:设A(m,n)
∵B(3,0),
∴OB=3.
由平移的性质可得
CE=OB=3,BE=OC=2,
∴CB=CE-BE=1.
∵S△DBE==4,
∴,
∴n=4,
∴S阴影=S△ACB==.
故选:C
【点拨】本题主要考查了坐标系中的平移变换.掌握平移的性质并能求出n的值是解题的关键.
17.A
【分析】根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为,当n为偶数时为,继而求得把正方形连续经过2021次这样的变换得到正方形的对角线交点M的坐标.
解:∵对角线交点M的坐标为,
根据题意得:第1次变换后的点M的对应点的坐标为,即,
第2次变换后的点M的对应点的坐标为:,即,
第3次变换后的点M的对应点的坐标为,即,
第n次变换后的点M的对应点的为:当n为奇数时为,当n为偶数时为,
∴连续经过2021次变换后,正方形的对角线交点M的坐标变为.
故选:A.
【点拨】此题考查了点的坐标变化,对称与平移的性质,得到规律:第n次变换后的对角线交点M的对应点的坐标为:当n为奇数时为,当n为偶数时为是解此题的关键.
18.D
【分析】根据图中各点的坐标的变化,依次写出,.再根据点的坐标变化的特点写出的坐标即可.
解:,
;
,
;
故选:D.
【点拨】此题考查了坐标与图形的变化,正确写出前几个点的坐标、找出坐标变化的规律是解答此题的关键.
19.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点拨】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
20.C
【分析】设平移后点、的对应点分别是、.分两种情况进行讨论:①在轴上,在轴上;②在轴上,在轴上.
解:设平移后点、的对应点分别是、.
分两种情况:
①在轴上,在轴上,
则横坐标为0,纵坐标为0,
,
,
点平移后的对应点的坐标是;
②在轴上,在轴上,
则纵坐标为0,横坐标为0,
,
,
点平移后的对应点的坐标是;
综上可知,点平移后的对应点的坐标是或.
故选:C.
【点拨】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
21.A
【分析】设AC与DE的交点为H,根据平移的性质可得,然后可得,过点A作AG⊥BC于点G,则AG即为点A到BC的距离,然后利用等积法可进行求解.
解:设AC与DE的交点为H,如图所示:
∵,将三角形沿直线向右平移3个单位得到三角形,连接,
∴根据平移的性质知,,故①正确;
∵,
∴,故②正确;
∵,,
∴四边形的周长为
,故③正确;
∵,
∴,故④正确;
过点A作AG⊥BC于点G,则AG即为点A到BC的距离,如图,
∵,
∴,故⑤正确;
∴正确的个数有5个;
故选A.
【点拨】本题主要考查平移的性质及平行线的性质与判定,熟练掌握平移的性质是解题的关键.
22.D
【分析】过P作PM⊥OB于M,并反向延长交CD于N,设P(x,y),根据S△POB:S△POC=5:6,于是得到x=2y;由于S△PCD=S△PBD,于是得到×7 (3-y)=18-×7(3-y)-×3x-×5y,最后解方程组即可得到结论.
解:如图,过P作PM⊥OB于M,交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(x,y),
∵S△POB:S△POC=5:6,
∴5××3x=6××5y,
∴x=2y,①
∵S△PCD=S△PBD,
∴×7 (3﹣y)=18﹣×7(3﹣y)﹣×3x﹣×5y,②
由①、②解得x=4,y=2,
∴P(4,2),
故选:D.
【点拨】本题主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,作辅助线构造平行线和垂线是解题的关键.
23.42
【分析】求出m+n取最小值时,m、n的关系式,又,2,3,4,5,6,计算的值,比较求出最大的值.
解:由题意得,
则,
∵,,且i、j都是整数,
∴当时,取最小值13,
此时,
∴,
又,2,3,4,5,6.
则时,;m=2时,;时,;时,;时,;时,.
则的最大值是42.
故答案为:42.
【点拨】本题考查了利用坐标表示位置,几何变换的代数表示法,属于新定义型题目,解答本题需要同学们仔细审题,理解位置数是怎样规定的.
24.(-2,2)
【分析】根据“帅”和“马”的位置,可确定原点O的位置,即可得答案.
解:如下图,
∵“帅”位于点(0, 1),“马”位于点(3, 1),
∴原点O的位置如上图,
∴“兵”位于点(-2,2),
故答案为:(-2,2).
【点拨】本题考查了平面上物体位置的确定,解题的关键是确定原点O的位置.
25. (9,6)
【分析】根据题意,找出题目的规律,中含有4个数,中含有9个数,中含有16个数,……,中含有64个数,且奇数行都是从左边第一个数开始,然后根据这个规律即可得出答案.
解:根据题意,如图:
∴有序数对的数是;
由图可知,中含有4个数,中含有9个数,中含有16个数;
……
∴中含有64个数,且奇数行都是从左边第一个数开始,
∵,
∴是第九行的第6个数;
∴数位置为有序数对是(9,6).
故答案为:;(9,6).
【点拨】此题考查数字的变化规律,找出数字之间的联系,得出运算规律,解决问题.
26.18.
【分析】(m,n)的规律是m表示从上到下第m行又表示第m行有m个数,n表示该行从左到右第n个数,(1,1)第一行1个数是1,(2,2)表示的数是1+2=3,(3,3)表示的数是1+2+3=6,
…以此类推(m-1,m-1)表示的数是1+2+3+…+m-1=,为此(m,n)表示的数是+n,当m=4,n=2表示的数为×4×3+2=6+2=8,为此(6,3)只要求代数式的即可.
解:先计算前m-1行最后一个数为:1+2+3+…+m-1=,
再求(m,n)表示的数,第m行从左到右第n个数,即为+n,
当m=6,n=3,代入+n=×6×5+3=18,
(6,3)表示的整数是18.
故答案为:18.
【点拨】本题考查数字规律探索问题,关键用数形结合思想,发相规律,用代数式表示规律,用规律解决问题.
27.或,或
【分析】首先根据条件画出图,如图所示,当点在轴上时,则为底,点的纵坐标数值为高,根据面积公式求出底的长度,即可得到点坐标;当点在轴上时,可分析出不可能在正半轴,故只能在负半轴,如图,设出点坐标,用割补法表示的面积即可求得.
解:当点在轴上时,
解得:
所以点有两个,,
当点在轴上时,
点符合题意,当点向上移动时,面积变大,
在正半轴不存在符合条件的点.
设在轴负半轴上点,
则
即:
解得:
所以,点坐标为
故答案为:或或
【点拨】本题主要考查了分类讨论的数学思想,相关知识点有:割补法求面积,对点的位置进行分类讨论是解题的关键.
28.或##或
【分析】根据ABx轴,则的纵坐标相等,求得的值,进而确定的坐标,根据即可求解.
解:∵A(3a+6,a+4),B(﹣3,2),ABx轴,
∴,
解得,
∴,
∴,
设,
①当在的延长线上时,,
,
解得,
∴,
②当在线段上时,,
,
解得,
∴,
③当在的延长线上时,,不符合题意,
综上所述,点的坐标为或,
故答案为:或.
【点拨】本题考查了坐标与图形,数形结合求得点的坐标是解题的关键.
29.第二象限
【分析】根据得到分计算即可.
解:∵,
∴,
当时,
得,
此时经过第一象限;
当时,
得,
此时经过第四象限;
当时,
得,
此时经过第三象限;
故不经过第二象限.
故答案为:第二象限.
【点拨】本题考查了坐标与象限,正确分类是计算判断的关键.
30.三
【分析】把m看作常数,根据一元一次方程的解法求出x的表达式,再根据方程的解是负数列不等式并求解即可.
解:由,得
x=2+m.
∵关于x的方程的解是负数,
∴2+m<0,
解得m<-2
∴(m,m+2)在第三象限
故答案是:三.
【点拨】本题考查了一元一次方程的解与解不等式,把m看作常数求出x的表达式是解题的关键.
31.或
【分析】分点P在轴和轴上两种情况,进行讨论求解即可.
解:当点P在轴上时:,解得:,
∴,
∴;
当点P在轴上时:,解得:,
∴,
∴;
综上:点P的坐标为:或;
故答案为:或.
【点拨】本题考查坐标轴上点的特征.熟练掌握坐标轴上的点的横坐标或纵坐标为0,是解题的关键.
32.四
【分析】根据点A(m2﹣4,m+1)在y轴的非负半轴上可得,据此求出m的值,再根据各象限内点的坐标的符号进行判断即可.
解:∵点A(m2﹣4,m+1)在y轴的非负半轴上,
∴,
解得m=2,
∴m﹣1=1,1﹣2m=﹣3,
∵(1,﹣3)在第四象限,
∴点B(m﹣1,1﹣2m)在第四象限.
故答案为:四.
【点拨】本题主要考查了平面直角坐标系象限内点的坐标特征,准确计算是解题的关键.
33.(6,4)或(﹣4,﹣6)
【分析】设点P的横坐标为x,表示出纵坐标,然后列方程求出x,再求解即可.
解:设点P的横坐标为x,则点P的纵坐标为x-2,由题意得,
当点P在第一象限时,x+x-2=10,
解得x=6,
∴x-2=4,
∴P(6,4);
当点P在第三象限时,-x-x+2=10,
解得x=-4,
∴x-2=-6,
∴P(-4,-6).
故答案为(6,4)或(-4,-6).
【点拨】本题主要考查了点的坐标,读懂题目信息,理解“点角距离”的定义并列出方程是解题的关键.
34.(-5,0),(5,0),(0,4),(0,-4)
【分析】根据题意可知点C在x轴上或者在y轴上,通过分析,根据AC+BC=10,符合要求的有四种情况,可以确定点C的坐标.
解:第一种情况:当点C在x轴左半轴时,点C在点A的左侧.
若C在点A的右侧,只能当A与C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).
∵AC+BC=10,点A(-3,0),B(3,0),
∴(-3-x)+(3-x)=10.
解得,x=-5.
∴点C的坐标为(-5,0),点A(-3,0),B(3,0),
第二种情况:当点C在x轴左半轴时,点C在点B的右侧.
若C在点B的左侧,只能当与B,C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).
∵AC+BC=10,
∴[x-(-3)]+(x-3)=10.
解得,x=5.
∴点C的坐标为(5,0).
第三种情况:点C在y轴上方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y =52.
解得,y=±4.
∵点C在y轴上方,
∴点C的坐标为(0,4).
第四种情况:点C在y轴下方.
设点C的坐标为(0,y).
∵AC+BC=10,点A(-3,0),B(3,0),
∴AC=BC=5,32+y =52.
解得,y=±4.
∵点C在y轴下方,
∴点C的坐标为(0,-4).
故答案为(-5,0),(5,0),(0,4),(0,-4).
【点拨】本题考查的是坐标与图形的性质,熟练掌握图形与坐标的性质是解题的关键.
35.或
【分析】设点C的坐标为,求出的长,再根据三角形的面积公式列式计算即可.
解:设点C的坐标为,
∵,,
∴,
由题意得:,解得:或,
∴点C的坐标为或.
故答案为:或.
【点拨】本题主要考查的是三角形的面积、坐标与图形性质等知识点,正确表示出的长、灵活运用三角形的面积公式是解题的关键.
36.或
【分析】先画出图形,设点的坐标为,则,,再利用三角形的面积公式建立方程,解方程即可得.
解:由题意,画出图形如下:
设点的坐标为,
,,
,,
又的面积为,且轴轴,
,
解得或,
故点的坐标为或,
故答案为:或.
【点拨】本题考查了坐标与图形,利用三角形的面积公式正确建立方程是解题关键.
37.4
【分析】根据可知:点A在直线上,根据垂线段最短,可知:当点A与点B的连线与直线垂直时,线段最短,据此即可作答.
解:根据可知:点A在直线上,
根据垂线段最短,可知:当点A与点B的连线与直线垂直时,线段最短,
∵与直线垂直,直线与x轴平行,
∴轴,
∴点A与点B的横坐标相等,
∴,
即点A与点B的最小距离为4,
故答案为:4.
【点拨】本题考查了坐标系中两点之间的距离以及垂线段最短的知识,掌握垂线段最短是解答本题的关键.
38.
【分析】过点作轴于,过点作交的延长线于点,设交轴于点,证明,求出,即可解得.
解:如图,过点作轴于,过点作交的延长线于点,设交轴于点,
,
四边形为正方形,
,,
,
又,
,
≌,
,,
点的坐标为,
,,
,,
,
故答案为:.
【点拨】本题考查的是图形与坐标,正方形的性质,三角形全等的判定与性质,掌握利用垂直证明三角形全等是解题的关键.
39.
【分析】根据题意,确定图形从开始位置经过4次翻滚后点进行了一次循环回到对应位置,从而结合长方形周长为,依据即可得到答案.
解:如图所示:
,
观察图形可知,经过4次翻滚后点进行了一次循环回到对应位置,,
∵长方形的周长为:,
每一次完整循环,相当于对应点的横坐标,纵坐标保持不变,
,即经过了次完整的循环后再向前翻滚次,是的对应点,
∴经过次翻滚后点对应点的坐标为,即,
故答案为:.
【点拨】本题考查动点坐标规律,读懂题意,理解图形从开始位置经过4次翻滚后点进行了一次循环回到对应位置是解决问题的关键.
40.
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、、…每偶数之间的B相差6个单位长度,根据这个规律可以求得的坐标.
解:∵点,,
∴,,
∴,
∴,
∴的横坐标为:6,且,点的纵坐标为:2
∴的横坐标为:,点的纵坐标为:2
∴点的横坐标为:.
∴点的纵坐标为:2.
故点的坐标为.
故答案为:.
【点拨】本题考查点的坐标规律变换,解题关键是通过图形旋转,找到所有B点之间的关系.
41.(,)
【分析】依据对应点的坐标变化,即可得到三角形ABC向左平移2个单位,向上平移3个单位后得到三角形A′B′C′,进而得出点P′的坐标.
解:由图可得,C(2,0),C'(0,3),
∴三角形ABC向左平移2个单位,向上平移3个单位后得到三角形A′B′C′,
又∵点P(,﹣)为三角形ABC内部一点,且与三角形A′B′C′内部的点P′对应,
∴对应点P′的坐标为(﹣2,﹣+3),即P'(,),
故答案为:(,).
【点拨】此题主要考查了坐标与图形变化,关键是注意观察组成图形的关键点平移后的位置.解题时注意:横坐标,右移加,左移减;纵坐标,上移加,下移减.
42.(2,1)
【分析】根据A和A1的坐标得出四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,则B的平移方法与A点相同,即可得到答案.
解:由A(-3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(-4,3),
∴B1的坐标为(2,1),
故答案为:(2,1).
【点拨】此题主要考查了点的平移规律与图形的平移,关键是掌握平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减.
43.①②④
【分析】根据平移的性质先求出点C和点D的坐标,得到点A和点D的纵坐标相同,进而得到轴,再利用平移的性质来求解.
解:∵A(a,b),B(m,b + 1)(a≠m + 1)两点同时向右平移h(h > 0)个单位,再向下平移1个单位得到C,D两点(点A对应点C),
一个点向右平移h个单位,则该点的横坐标加h;一个点向下平移1个单位,则该点的纵坐标减1,
∴,,
此时点A和点D的纵坐标相同,
∴轴.
根据平移的性质可知:,故①正确;
AD平行于x轴,l垂直于AD
那么l也垂直于x轴,故②正确;
由图可知:因为a≠m + 1,所以A、B、C三点不可能在同一条直线上,故③错误;
当DE取最小值时,点E与点P重合时,
此时点E的坐标为(m,b),故④正确.
综上所述,正确的有:①②④.
【点拨】本题主要考查了平移的性质,理解平移的性质和求出平移后点C和D的坐标是解答关键.
44.
【分析】根据平移的性质,可得答案.
解:过点作,如图,
,
,,
,
的面积,
平移不改变图形的形状和大小,
△的面积为,
故答案为:
中小学教育资源及组卷应用平台
【点拨】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
