沪科版七下数学 8.3平方差公式与完全平方公式(第2课时)课件
文档属性
| 名称 | 沪科版七下数学 8.3平方差公式与完全平方公式(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 230.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-12 09:49:52 | ||
图片预览







文档简介
课件24张PPT。
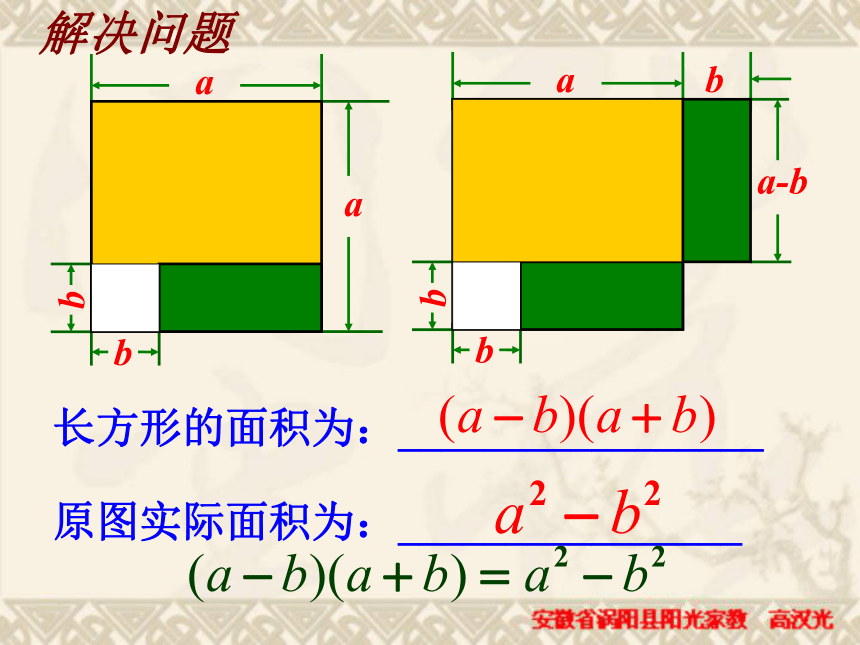
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗?
原图实际面积为:________________长方形的面积为:_________________bab解决问题探究:计算下列多项式的积,你能发现什么规律?
(x+3)(x-3)= ;
(m+2)(m-2)= ;
(2x+1)(2x-1)= ;[想一想]:这几道题目有什么共同特点?
从计算结果你能发现什么规律?猜想:(a+b)(a-b)= ? =x2-32x2-9m2-4=m2-224x2-1=(2x)2-12a2-b2a2-ab+ab+b2(a+b)(a-b) ==a2-b2 (a+b)(a-b)=a2-b2两个数的和与这两个数的差的积,等于这两个数的平方差.
公式的结构特征:(1)左边是两个二项式相乘,这两项中有一
项完全相同,另一项互为相反数.(2)右边是乘式中两项的平方差(相同项的
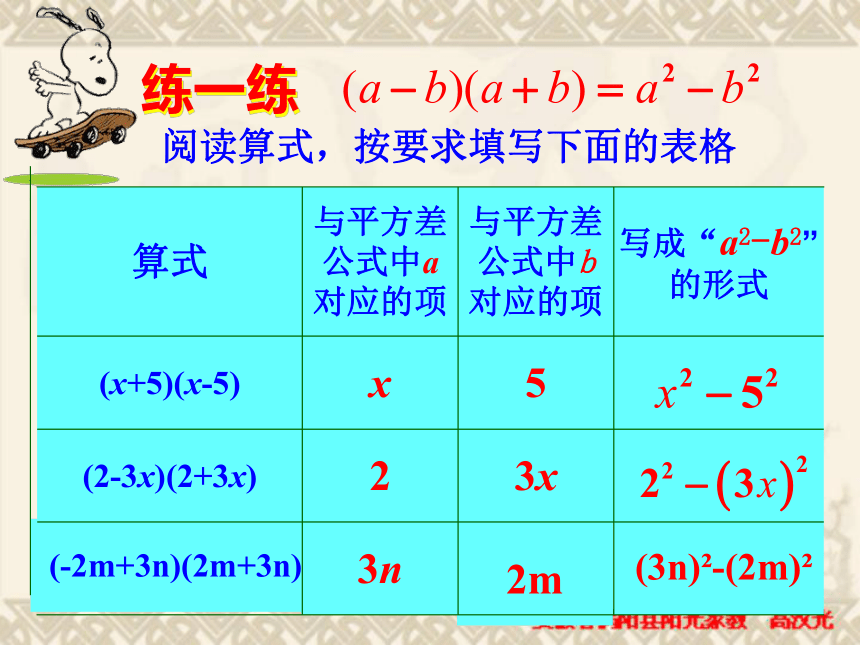
平方减去相反项的平方).(3)公式中的a,b可以代表数,字母,单项式或者多项式.平方差公式:练一练阅读算式,按要求填写下面的表格2m3n (-2m+3n)(2m+3n)3x2(2-3x)(2+3x)5x(x+5)(x-5)写成“a2-b2”的形式与平方差公式中b对应的项与平方差公式中a对应的项算式(3n)2-(2m)2例1、计算:(x+3)(x-3)=
(2a+3b)(2a-3b)= (-3+2a)(-2a-3)运用平方差公式计 算: ① (x+1)(x-1) = ② (m+2)(m-2)= ③ (2x+1)(2x-1) = x2-14x2-1m2-4④ (x+5y)(x-5y)=x2-25y2练一练下列计算是否正确?如不正确应怎样改正?
1.(a-4)(a+4)=a2-4 ( )
2.(2x+5)(2x-5)=2x2-25 ( )
3.(-a-b)(a+b)=a2-b2 ( )
4.(mn-1)(mn+1)=mn2-1 ( )××××运用平方差公式计算:
1.(a+b)(-b+a)=
2.(-a-b)(a-b)=
3.(3a+2b)(3a-2b)=
4.(a5-b2)(a5+b2)=a2-b2b2-a29a2-4b2a10-b4判断下列式子是否可用平方差公式。 (1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 )(-4k3+3y2)(-4k3-3y2)
是否是是是是否例2、计算:
(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5) 解:(1) 102×98=(100+2)(100-2)=1002-22=10000-4=9996(2)(y+2)(y-2)-(y-1)(y+5)
=y2 -22-(y2+4y-5)=y2-4-y2-4y+5=-4y+1注:必须符合平方差公式特征的代数式才能用平方差公式例3 计算: (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)解:(1)原式= a2( a2-b2)+a2b2=a4-a2b2+a2b2=a4(2)原式=(2 x )2 -25- (4 x 2-6 x )=4 x 2 -25- 4 x 2+6 x =6 x -25例4 计算:
1.(a-b)(a+b)(a2+b2)
2.(a+b+c)(a+b-c)
=(a2-b2)(a2+b2)=(a2)2-(b2)2=a4-b4=[(a+b)+c][(a+b)-c]=(a+b)2-c2=(a+b)(a+b)-c2=a2+2ab+b2-c2例5计算:15.3.1 平方差公式20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1例6.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-135.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )= -16y2+1+12y2-12y-9= -4y2-12y-85.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )运用平方差公式计算:
(1) (3x+2)(3x-2)
(2) (b+2a)(2a-b)
(3) (-x+2y)(-x-2y)
(4) (a-b+c)(a-b-c)巩固练习运用平方差公式计算:
(5) 102×98
(6) (a+3)(a-3)(a2+9)
(7) (x-1)(x+1)(x2+1)(x4+1)(x8+1)
(8) (2+1)(22+1)(24+1)(28+1)(216+1)巩固练习(1)16x2-81; (2)x2-y2+2y-1;
(3)x2-2x+1-y2; (4)m4-8m2n2+16n4.-4xy; -81. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。两数和与这两数差的积,等于它们的平方差。2.应用平方差公式 时要注意一些什么?运用平方差公式时,要紧扣公式的特征, 找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗?
原图实际面积为:________________长方形的面积为:_________________bab解决问题探究:计算下列多项式的积,你能发现什么规律?
(x+3)(x-3)= ;
(m+2)(m-2)= ;
(2x+1)(2x-1)= ;[想一想]:这几道题目有什么共同特点?
从计算结果你能发现什么规律?猜想:(a+b)(a-b)= ? =x2-32x2-9m2-4=m2-224x2-1=(2x)2-12a2-b2a2-ab+ab+b2(a+b)(a-b) ==a2-b2 (a+b)(a-b)=a2-b2两个数的和与这两个数的差的积,等于这两个数的平方差.
公式的结构特征:(1)左边是两个二项式相乘,这两项中有一
项完全相同,另一项互为相反数.(2)右边是乘式中两项的平方差(相同项的
平方减去相反项的平方).(3)公式中的a,b可以代表数,字母,单项式或者多项式.平方差公式:练一练阅读算式,按要求填写下面的表格2m3n (-2m+3n)(2m+3n)3x2(2-3x)(2+3x)5x(x+5)(x-5)写成“a2-b2”的形式与平方差公式中b对应的项与平方差公式中a对应的项算式(3n)2-(2m)2例1、计算:(x+3)(x-3)=
(2a+3b)(2a-3b)= (-3+2a)(-2a-3)运用平方差公式计 算: ① (x+1)(x-1) = ② (m+2)(m-2)= ③ (2x+1)(2x-1) = x2-14x2-1m2-4④ (x+5y)(x-5y)=x2-25y2练一练下列计算是否正确?如不正确应怎样改正?
1.(a-4)(a+4)=a2-4 ( )
2.(2x+5)(2x-5)=2x2-25 ( )
3.(-a-b)(a+b)=a2-b2 ( )
4.(mn-1)(mn+1)=mn2-1 ( )××××运用平方差公式计算:
1.(a+b)(-b+a)=
2.(-a-b)(a-b)=
3.(3a+2b)(3a-2b)=
4.(a5-b2)(a5+b2)=a2-b2b2-a29a2-4b2a10-b4判断下列式子是否可用平方差公式。 (1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 )(-4k3+3y2)(-4k3-3y2)
是否是是是是否例2、计算:
(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5) 解:(1) 102×98=(100+2)(100-2)=1002-22=10000-4=9996(2)(y+2)(y-2)-(y-1)(y+5)
=y2 -22-(y2+4y-5)=y2-4-y2-4y+5=-4y+1注:必须符合平方差公式特征的代数式才能用平方差公式例3 计算: (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)解:(1)原式= a2( a2-b2)+a2b2=a4-a2b2+a2b2=a4(2)原式=(2 x )2 -25- (4 x 2-6 x )=4 x 2 -25- 4 x 2+6 x =6 x -25例4 计算:
1.(a-b)(a+b)(a2+b2)
2.(a+b+c)(a+b-c)
=(a2-b2)(a2+b2)=(a2)2-(b2)2=a4-b4=[(a+b)+c][(a+b)-c]=(a+b)2-c2=(a+b)(a+b)-c2=a2+2ab+b2-c2例5计算:15.3.1 平方差公式20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1例6.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-135.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )= -16y2+1+12y2-12y-9= -4y2-12y-85.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )运用平方差公式计算:
(1) (3x+2)(3x-2)
(2) (b+2a)(2a-b)
(3) (-x+2y)(-x-2y)
(4) (a-b+c)(a-b-c)巩固练习运用平方差公式计算:
(5) 102×98
(6) (a+3)(a-3)(a2+9)
(7) (x-1)(x+1)(x2+1)(x4+1)(x8+1)
(8) (2+1)(22+1)(24+1)(28+1)(216+1)巩固练习(1)16x2-81; (2)x2-y2+2y-1;
(3)x2-2x+1-y2; (4)m4-8m2n2+16n4.-4xy; -81. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。两数和与这两数差的积,等于它们的平方差。2.应用平方差公式 时要注意一些什么?运用平方差公式时,要紧扣公式的特征, 找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结
