2022—2023学年华东师大版数学八年级下册17.1.1变量与函数 课件 (共23张PPT)
文档属性
| 名称 | 2022—2023学年华东师大版数学八年级下册17.1.1变量与函数 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 21:58:46 | ||
图片预览







文档简介
(共23张PPT)
17.1变量与函数
我们所处的世界时刻都在发生着变化
情景引入
要如何来研究各种运动变化的规律呢
情景引入
数学上常用变量与函数来刻画各种运动变化
问题1
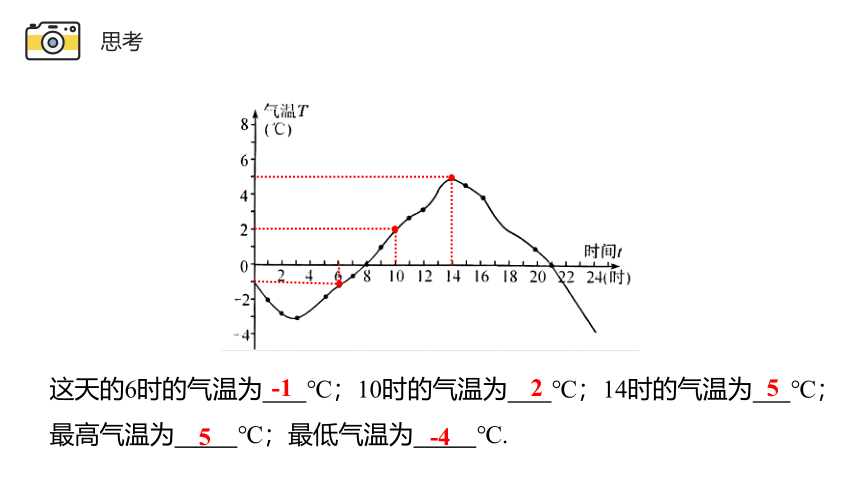
下图是某地一天内的气温变化图.
思考
你能从图中看到哪些信息?
这天的6时的气温为 ℃;10时的气温为 ℃;14时的气温为 ℃; 最高气温为 ℃;最低气温为 ℃.
-1
5
-4
2
5
思考
这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
这一天中,3时~14时的气温在逐渐升高;0时~3时和14时~24时的气温在逐渐降低.
思考
从图中我们还可以看到,随着时间 t(时)的变化,相应地,气温T(℃)也随之变化.
总结
观察上表,说一说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
周 岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁时的体重(kg),如下表:
随着年龄的增长,体重也随着增长;且在1-2周岁体重增加较快.
问题2
思考
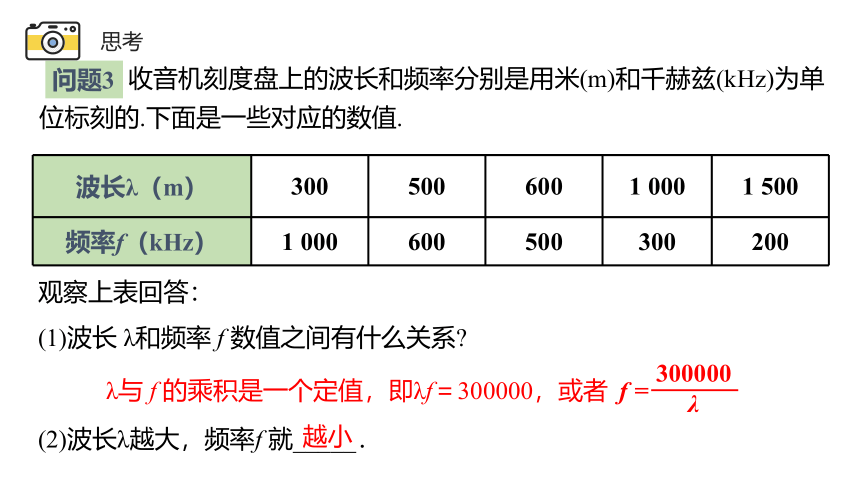
观察上表回答:
(1)波长 λ和频率 f 数值之间有什么关系
(2)波长λ越大,频率f 就_____.
收音机刻度盘上的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值.
波长λ(m) 300 500 600 1 000 1 500
频率f(kHz) 1 000 600 500 300 200
λ与 f 的乘积是一个定值,即λf=300000,或者
300000
λ
f =
越小
问题3
思考
由此可以看出,圆的半径越大,它的面积就______.
圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=____.
利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:
越大
半径r(cm) 1 1.5 2 2.6 3.2 ...
圆面积S(cm2) ...
πr2
π
2.25π
4π
6.76π
10.24π
问题4
思考
在上述4个问题中,都是一些变化的过程,出现了各种各样的数量,你认为可以怎样分类?
思考
数值发生变化的量
变量
数值始终不变的量
常量
问题1中的时间t、气温T;
问题3中的300000;
问题4中的π.
问题2中的周岁、体重;
问题3中的波长λ、频率f;
问题4中的圆面积S、半径r.
引入新知(书本第30页)
变量
在某一变化过程中,可以取不同数值的量,叫做变量.
即数值发生变化的量为变量.
常量
在某一变化过程中,取值始终保持不变的量,叫做常量.即数值始终不变的量为常量.
小试牛刀
例1.列车从甲地驶往乙地,在 16:17 到 16:22 这个时段,列车在匀速行驶的过程中,有哪些量?在这些量中哪些是常量?哪些是变量?
常量
速度:电子显示屏上的“350km/h”
路程:甲乙两地之间的路程
变量
时间:行驶的时间一直在变
距离:和甲的距离越来越大
和乙的距离越来越小
1.指出下列变化过程中的变量和常量:
(1)汽油的价格是7.4元/升,加油 x 升,车主加油付油费为 y 元;
(2)小明看一本200 页的小说,看完这本小说需要t 天,平均每天所看的页数为 n
(3)用长为40 cm 的绳子围矩形,围成的矩形一边长为 x cm,其面积为 S cm2.
(4)若直角三角形中的一个锐角的度数为α°,则另一锐角的度数β°与α°间的关系式是β=90°-α.
红色框表示常量;蓝色框表示变量.
It's your turn
常量一定是数字吗?
2.填一填
(1)某人持续以a米/分的速度用t分钟时间跑了s米,其中常量是 ,变量是 .
(2)s米的路程,不同的人以不同的速度a米/分各需跑的时间为t分钟,其中常量是_____,变量是 .
(3)根据上面的叙述,写出一句关于常量与变量的结论 .
a
s
a,t
t,s
在不同的条件
下,常量与变量是相对的
It's your turn
在前面的4个问题中,各个变化过程有没有什么共同之处?
思考
问题1:随着时间的变化,气温也随之变化.
问题2:随着年龄的变化,体重也随之变化.
问题3:随着波长的变化,频率也随之变化.
问题4:随着半径的变化,面积也随之变化.
都出现了两个变量,且两个变量相互依赖、密切相关.
当其中一个变量变化时,另一个变量也随着发生变化;当其中一个变量确定时,另一个变量也随着确定.
引入新知(书本第30页)
函数
一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
函数三要素
(1)有两个变量
(2)一个变量的数值随着另一个变量数值的变化而变化
(3)对于自变量的每一个值,函数有且仅有一个值与之
对应
1.下列关系式当中,y 不是 x 的函数的是 ( )
A. y = 2x - 3
B. y = x2 + 3
C. y = 2|x| + 3
D. y2 - 3x = 0
D
小试牛刀
下列关于变量 x ,y 的关系式: y = 2x + 3; y = x2 + 3; y = 2|x|;④ ;⑤y2 - 3x = 10,其中表示 y 是 x 的函数关系的是 .
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
方法
一个 x 值有两个 y 值与它相对应
It's your turn
图象法
列表法
解析法
波长λ(m) 300 500 600 1000 1500
频率f(kHz) 1000 600 500 300 200
S=πr2
300000
λ
f =
思考
我们可以怎么表示函数的关系呢?
解析法 列表法 图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格表示函数关系的方法
问题2、3
具体反映了函数随自变量变化的数值对应关系
用数学式子表示函数关系的方法
问题1
准确反映了函数随自变量变化的数量关系
用图象表示两个变量间的函数关系的方法
问题3、4
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法
新知引入(书本第30页)
在某一变化过程中,数值发生变化的量为变量,数值始终不变的量为常量.
解析法,列表法和图象法
变量与函数的概
念及其表示方法
常量与变量
函数
一般地,如果在一个变化过程中有两个变量x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
函数的表示方法
总结
下课!
17.1变量与函数
我们所处的世界时刻都在发生着变化
情景引入
要如何来研究各种运动变化的规律呢
情景引入
数学上常用变量与函数来刻画各种运动变化
问题1
下图是某地一天内的气温变化图.
思考
你能从图中看到哪些信息?
这天的6时的气温为 ℃;10时的气温为 ℃;14时的气温为 ℃; 最高气温为 ℃;最低气温为 ℃.
-1
5
-4
2
5
思考
这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
这一天中,3时~14时的气温在逐渐升高;0时~3时和14时~24时的气温在逐渐降低.
思考
从图中我们还可以看到,随着时间 t(时)的变化,相应地,气温T(℃)也随之变化.
总结
观察上表,说一说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
周 岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁时的体重(kg),如下表:
随着年龄的增长,体重也随着增长;且在1-2周岁体重增加较快.
问题2
思考
观察上表回答:
(1)波长 λ和频率 f 数值之间有什么关系
(2)波长λ越大,频率f 就_____.
收音机刻度盘上的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值.
波长λ(m) 300 500 600 1 000 1 500
频率f(kHz) 1 000 600 500 300 200
λ与 f 的乘积是一个定值,即λf=300000,或者
300000
λ
f =
越小
问题3
思考
由此可以看出,圆的半径越大,它的面积就______.
圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=____.
利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:
越大
半径r(cm) 1 1.5 2 2.6 3.2 ...
圆面积S(cm2) ...
πr2
π
2.25π
4π
6.76π
10.24π
问题4
思考
在上述4个问题中,都是一些变化的过程,出现了各种各样的数量,你认为可以怎样分类?
思考
数值发生变化的量
变量
数值始终不变的量
常量
问题1中的时间t、气温T;
问题3中的300000;
问题4中的π.
问题2中的周岁、体重;
问题3中的波长λ、频率f;
问题4中的圆面积S、半径r.
引入新知(书本第30页)
变量
在某一变化过程中,可以取不同数值的量,叫做变量.
即数值发生变化的量为变量.
常量
在某一变化过程中,取值始终保持不变的量,叫做常量.即数值始终不变的量为常量.
小试牛刀
例1.列车从甲地驶往乙地,在 16:17 到 16:22 这个时段,列车在匀速行驶的过程中,有哪些量?在这些量中哪些是常量?哪些是变量?
常量
速度:电子显示屏上的“350km/h”
路程:甲乙两地之间的路程
变量
时间:行驶的时间一直在变
距离:和甲的距离越来越大
和乙的距离越来越小
1.指出下列变化过程中的变量和常量:
(1)汽油的价格是7.4元/升,加油 x 升,车主加油付油费为 y 元;
(2)小明看一本200 页的小说,看完这本小说需要t 天,平均每天所看的页数为 n
(3)用长为40 cm 的绳子围矩形,围成的矩形一边长为 x cm,其面积为 S cm2.
(4)若直角三角形中的一个锐角的度数为α°,则另一锐角的度数β°与α°间的关系式是β=90°-α.
红色框表示常量;蓝色框表示变量.
It's your turn
常量一定是数字吗?
2.填一填
(1)某人持续以a米/分的速度用t分钟时间跑了s米,其中常量是 ,变量是 .
(2)s米的路程,不同的人以不同的速度a米/分各需跑的时间为t分钟,其中常量是_____,变量是 .
(3)根据上面的叙述,写出一句关于常量与变量的结论 .
a
s
a,t
t,s
在不同的条件
下,常量与变量是相对的
It's your turn
在前面的4个问题中,各个变化过程有没有什么共同之处?
思考
问题1:随着时间的变化,气温也随之变化.
问题2:随着年龄的变化,体重也随之变化.
问题3:随着波长的变化,频率也随之变化.
问题4:随着半径的变化,面积也随之变化.
都出现了两个变量,且两个变量相互依赖、密切相关.
当其中一个变量变化时,另一个变量也随着发生变化;当其中一个变量确定时,另一个变量也随着确定.
引入新知(书本第30页)
函数
一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
函数三要素
(1)有两个变量
(2)一个变量的数值随着另一个变量数值的变化而变化
(3)对于自变量的每一个值,函数有且仅有一个值与之
对应
1.下列关系式当中,y 不是 x 的函数的是 ( )
A. y = 2x - 3
B. y = x2 + 3
C. y = 2|x| + 3
D. y2 - 3x = 0
D
小试牛刀
下列关于变量 x ,y 的关系式: y = 2x + 3; y = x2 + 3; y = 2|x|;④ ;⑤y2 - 3x = 10,其中表示 y 是 x 的函数关系的是 .
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
方法
一个 x 值有两个 y 值与它相对应
It's your turn
图象法
列表法
解析法
波长λ(m) 300 500 600 1000 1500
频率f(kHz) 1000 600 500 300 200
S=πr2
300000
λ
f =
思考
我们可以怎么表示函数的关系呢?
解析法 列表法 图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格表示函数关系的方法
问题2、3
具体反映了函数随自变量变化的数值对应关系
用数学式子表示函数关系的方法
问题1
准确反映了函数随自变量变化的数量关系
用图象表示两个变量间的函数关系的方法
问题3、4
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法
新知引入(书本第30页)
在某一变化过程中,数值发生变化的量为变量,数值始终不变的量为常量.
解析法,列表法和图象法
变量与函数的概
念及其表示方法
常量与变量
函数
一般地,如果在一个变化过程中有两个变量x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
函数的表示方法
总结
下课!
