北师大版 九年级上册1.1 菱形的性质与判定 课件 (共39张PPT)
文档属性
| 名称 | 北师大版 九年级上册1.1 菱形的性质与判定 课件 (共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 06:52:48 | ||
图片预览









文档简介
(共39张PPT)
1.1 菱形的性质与判定
第一章 特殊平行四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
菱形的定义及其性质
菱形的判定
知1-讲
感悟新知
知识点
菱形的定义及其性质
1
1.定义 有一组邻边相等的平行四边形叫做菱形 .
感悟新知
知1-讲
特别提醒
◆菱形必须满足两个条件:
一是平行四边形;
二是一组邻边相等 .
二者必须同时具备,缺一不可 .
◆菱形的定义既是菱形的基本性质,也是菱形的基本判定方法 .
感悟新知
2.性质如下表
知1-讲
图形 性质 数学表达式
菱形的四条边相等 ∵四边形 ABCD 是菱形,
∴ AB=BC=CD=AD
菱形的对角线互相垂直 ∵四边形 ABCD 是菱形,
∴ BD ⊥ AC
菱形是轴对称图形,它有两条对称轴
感悟新知
特别提醒: (1) 菱形的性质可以用来证明线段相等,角相等以及直线的平行、垂直等关系 . (2)由菱形的性质与勾股定理的联系,可得对角线与边之间的关系,即边长的平方等于两条对角线长一半的平方和 . (3)如果菱形的一个内角为 60°,那么菱形的两条边与较短的对角线构成的三角形为等边三角形 .
知1-讲
知1-练
感悟新知
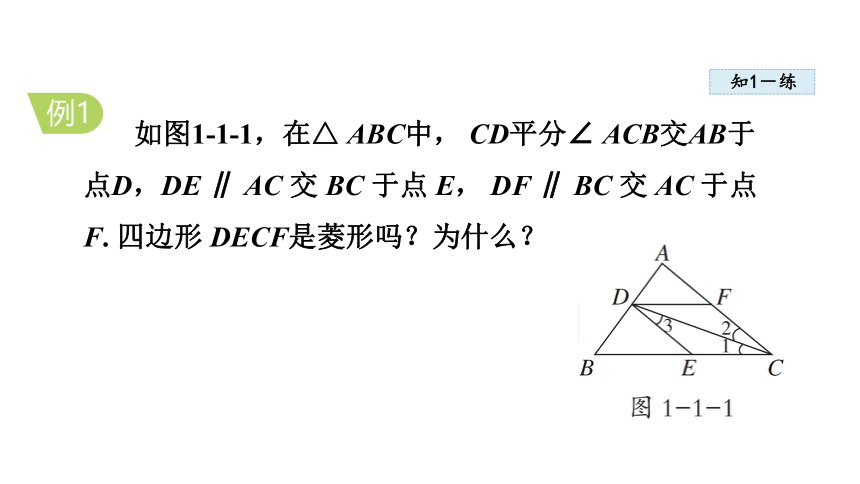
如图1-1-1,在△ ABC中, CD平分∠ ACB交AB于点D,DE ∥ AC 交 BC 于点 E, DF ∥ BC 交 AC 于点 F. 四边形 DECF是菱形吗?为什么?
例1
知1-练
感悟新知
解:四边形 DECF 是菱形 . 理由如下:
∵ DE ∥ FC, DF ∥ EC,
∴四边形 DECF 为平行四边形 .
∵ AC ∥ DE,∴∠ 2= ∠ 3.
∵ CD 平分∠ ACB,∴∠ 1= ∠ 2. ∴∠ 1= ∠ 3.
∴ DE=EC. ∴平行四边形 DECF 为菱形 .
解题秘方:紧扣菱形的定义中“两个条件” 进行判断 .
知1-练
感悟新知
1-1.如图,在平行四边形 ABCD 中, 点 O 是AD 的 中 点, 连接 CO并延长交 BA 的延长线于点 E,连接 AC, DE.
(1)求证: 四边形ACDE 是平行四边形;
知1-练
感悟新知
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠BEC=∠DCE.
∵点O是AD的中点,∴AO=DO.
又∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).∴AE=CD.
又∵AE∥DC,∴四边形ACDE是平行四边形.
知1-练
感悟新知
(2)若 AB=AC,判断四边形 ACDE 的形状,并说明理由 .
解:四边形ACDE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD.又∵AB=AC,∴CD=AC.
又由(1)可知四边形ACDE是平行四边形,
∴四边形ACDE是菱形.
感悟新知
知1-练
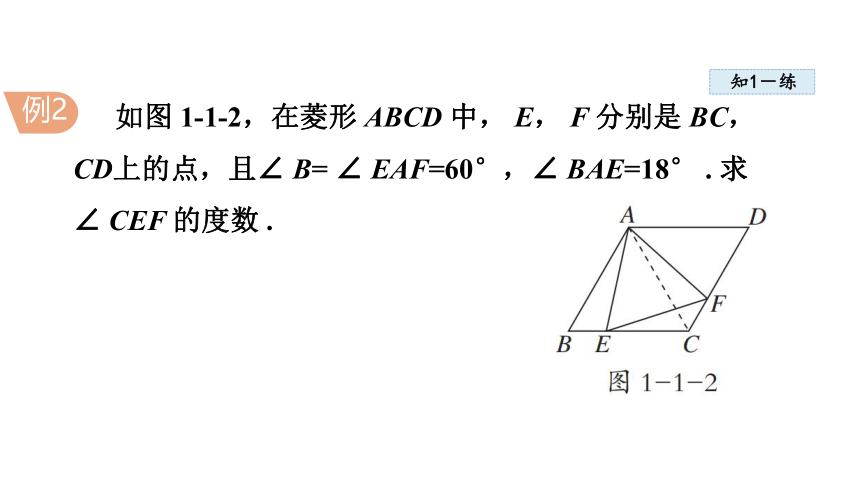
如图 1-1-2,在菱形 ABCD 中, E, F 分别是 BC, CD上的点,且∠ B= ∠ EAF=60°,∠ BAE=18° . 求∠ CEF 的度数 .
例2
知1-练
感悟新知
解题秘方:紧扣菱形的性质、三角形外角的性质求解 .
解:如图 1-1-2,连接 AC.
∵ 四边形 ABCD 是菱形,∠ B=60° ,
∴ AB=BC=CD=DA,∠ D= ∠ B=60° .
∴△ ABC 和△ ACD 均为等边三角形 .
∴ AB=AC,∠ B= ∠ ACF= ∠ BAC=60° .
∵∠ EAF=60°,∴∠ BAC= ∠ EAF.
知1-练
感悟新知
∴∠ BAE= ∠ CAF.
∴△ ABE ≌△ ACF ( ASA ) . ∴ AE=AF.
又∵∠ EAF=60°,∴△ EAF 是等边三角形 .
∴∠ AEF=60° .
∵∠ AEC= ∠ B+ ∠ BAE= ∠ AEF+ ∠ CEF,
∴ 60° +18° =60° + ∠ CEF.
∴∠ CEF=18° .
知1-练
感悟新知
2-1.如图, 在菱形ABCD 中, ∠ BAD=80 °, AB 的垂直平分线交对角线 AC 于点 F, E 为垂足, 连接DF,则∠ CDF 的度数为_____ .
60°
知1-练
感悟新知
如图 1-1-3,四边形 ABCD 是菱形,对角线 AC, BD相交于点 O,且 AB=2.
例3
知1-练
感悟新知
解题秘方:紧扣菱形边、对角线的性质,根据菱形的对角线互相垂直,利用勾股定理求线段长是解决问题的关键 .
知1-练
感悟新知
(1)求菱形 ABCD 的周长;
解:∵四边形 ABCD 是菱形,AB=2,
∴菱形 ABCD 的周长为 2× 4= 8.
知1-练
感悟新知
(2)若 AC=2,求 BD 的长 .
解:∵四边形 ABCD 是菱形, AC=2,
∴ AC ⊥ BD, BO= BD, AO= AC= 1.
在 Rt △ AOB 中,∵ AB=2, AO=1,
∴ BO = = = .
∴ BD = 2BO =2 .
知1-练
感悟新知
3-1. [ 中考· 安徽 ] 如图,在菱形 ABCD 中,AB=2, ∠ A=120 °,过菱形 ABCD 的对称中心 O 分别作边 AB, BC的垂线,交各边于点 E,F, G, H, 则 四 边形EFGH 的周长为( )
A.3+ B.2+2
C.2+ D.1+2
A
感悟新知
知1-练
如图 1-1-4,在菱形 ABCD 中,对角线交于点 O,∠ ABC 与∠ BAD 的度数比为 1∶2,菱形 ABCD的周长是 48. 求:
例4
知1-练
感悟新知
解题秘方:紧扣菱形的性质和面积公式求解 .
知1-练
感悟新知
(1)菱形 ABCD 的两条对角线的长度;
解:∵在菱形 ABCD 中,∠ ABC 与∠ BAD 的度数比
为 1 ∶ 2,∴ ∠ ABC=60°,∠ BAD=120°, AC ⊥ BD.
∴ ∠ ABO=30° .
∵ 菱形 ABCD 的周长是 48,∴ AB=BC=DC=AD=12.
∴ AO=6. ∴ BO= = =6 ,
AC=12,∴ BD=12 .
知1-练
感悟新知
(2)菱形 ABCD 的面积 .
解:S 菱形 ABCD= AC· BD
= × 12× 12 =72 .
菱形面积的两种计算方法
1. 一边与这边上的高的乘积;
2. 两条对角线乘积的一半 .
知1-练
感悟新知
4-1.如图,在菱形ABCD 中,对角线 AC和 BD 相交于点 O,E 是 BC 的中点,连接AE. 若∠ ABC=60°,BE=2 cm,求: (1)菱形ABCD的周长;
知1-练
感悟新知
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵E为BC的中点,BE=2 cm,
∴BC=2BE=4 cm.
∴菱形ABCD的周长为4BC=16 cm.
知1-练
感悟新知
(2)菱形ABCD的面积.
感悟新知
知2-讲
知识点
菱形的判定
2
1.判定定理 1 对角线互相垂直的平行四边形是菱形 .
数学表达式: 如图 1-1-5,在 ABCD 中,
∵ AC ⊥ BD,∴ ABCD 是菱形 .
感悟新知
知2-讲
2. 判定定理 2 四边相等的四边形是菱形 .
数学表达式: 如图 1-1-5,在四边形 ABCD 中,
∵ AB=BC=CD=DA,∴四边形 ABCD 是菱形 .
知2-讲
感悟新知
特别提醒
●菱形的判定定理和性质定理是互逆定理.
●判定菱形的常见思路:
四边形
平行四边形
知2-练
感悟新知
如图 1-1-6,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 作直线 EF ⊥ BD,分别交 AD, BC 于点 E 和点 F, 连接 BE, DF. 求证: 四 边形BEDF 是菱形 .
例5
知2-练
感悟新知
解题秘方:紧扣对角线垂直这一条件,从判定平行四边形入手判定菱形 .
证明: ∵四边形 ABCD 是平行四边形,
∴ OB=OD, AD ∥ BC.
∴∠ EDO= ∠ FBO,∠ OED= ∠ OFB.
∴△ OED ≌△ OFB(AAS) . ∴ DE=BF.
又∵ DE ∥ BF,∴四边形 BEDF 是平行四边形 .
又∵ EF ⊥ BD,∴四边形 BEDF 是菱形 .
知2-练
感悟新知
5-1.如图, 在三角形纸片 ABC 中, AD 是△ ABC 的角平分线,把△ ABC 进行折叠,使点A 与点 D 重合,折痕与AB 相交于点 E,与 AC相交于点 F. 求证:四边形 AEDF 是菱形 .
知2-练
感悟新知
证明:设AD与EF相交于点O.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵点A与点D关于直线EF对称,
∴EF⊥AD,∴∠AOE=∠AOF=90°.
又∵AO=AO,∴△AEO≌△AFO(ASA).
∴EO=FO.
知2-练
感悟新知
又∵点A与点D重合,∴AO=DO.
∴EF,AD互相平分.
∴四边形AEDF是平行四边形.
又∵AD⊥EF,∴四边形AEDF是菱形.
感悟新知
知2-练
如图 1-1-7,在四边形 ABCD 中, AD=BC,点 E, F, G,H 分别是 AB, CD, AC, BD 的中点,求证:四边形 EGFH 是菱形 .
例6
知2-练
感悟新知
解题秘方:紧扣题中中点条件与线段相等这一特征,从证四条边相等入手判定菱形 .
证明: ∵点 E, H 分别是 AB, BD 的中点,
∴ EH 为△ ABD 的中位线 . ∴ EH= AD.
同理可得 GF= AD, EG= BC, HF= BC.
∵ AD=BC,∴ EH =GF= EG = HF .
∴四边形 EGFH 是菱形 .
知2-练
感悟新知
6-1.四边形的四边长顺次为 a, b, c, d,且 a2+b2+c2+d2=ab+bc+cd+ad, 则此四边形一定是( )
A. 平行四边形 B. 长方形
C. 菱形 D. 正方形
C
菱形的性质与判定
边的关系
边的性质
对角线的性质
对角线的关系
菱形
定义
轴对称性
性质
判定
1.1 菱形的性质与判定
第一章 特殊平行四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
菱形的定义及其性质
菱形的判定
知1-讲
感悟新知
知识点
菱形的定义及其性质
1
1.定义 有一组邻边相等的平行四边形叫做菱形 .
感悟新知
知1-讲
特别提醒
◆菱形必须满足两个条件:
一是平行四边形;
二是一组邻边相等 .
二者必须同时具备,缺一不可 .
◆菱形的定义既是菱形的基本性质,也是菱形的基本判定方法 .
感悟新知
2.性质如下表
知1-讲
图形 性质 数学表达式
菱形的四条边相等 ∵四边形 ABCD 是菱形,
∴ AB=BC=CD=AD
菱形的对角线互相垂直 ∵四边形 ABCD 是菱形,
∴ BD ⊥ AC
菱形是轴对称图形,它有两条对称轴
感悟新知
特别提醒: (1) 菱形的性质可以用来证明线段相等,角相等以及直线的平行、垂直等关系 . (2)由菱形的性质与勾股定理的联系,可得对角线与边之间的关系,即边长的平方等于两条对角线长一半的平方和 . (3)如果菱形的一个内角为 60°,那么菱形的两条边与较短的对角线构成的三角形为等边三角形 .
知1-讲
知1-练
感悟新知
如图1-1-1,在△ ABC中, CD平分∠ ACB交AB于点D,DE ∥ AC 交 BC 于点 E, DF ∥ BC 交 AC 于点 F. 四边形 DECF是菱形吗?为什么?
例1
知1-练
感悟新知
解:四边形 DECF 是菱形 . 理由如下:
∵ DE ∥ FC, DF ∥ EC,
∴四边形 DECF 为平行四边形 .
∵ AC ∥ DE,∴∠ 2= ∠ 3.
∵ CD 平分∠ ACB,∴∠ 1= ∠ 2. ∴∠ 1= ∠ 3.
∴ DE=EC. ∴平行四边形 DECF 为菱形 .
解题秘方:紧扣菱形的定义中“两个条件” 进行判断 .
知1-练
感悟新知
1-1.如图,在平行四边形 ABCD 中, 点 O 是AD 的 中 点, 连接 CO并延长交 BA 的延长线于点 E,连接 AC, DE.
(1)求证: 四边形ACDE 是平行四边形;
知1-练
感悟新知
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠BEC=∠DCE.
∵点O是AD的中点,∴AO=DO.
又∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).∴AE=CD.
又∵AE∥DC,∴四边形ACDE是平行四边形.
知1-练
感悟新知
(2)若 AB=AC,判断四边形 ACDE 的形状,并说明理由 .
解:四边形ACDE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD.又∵AB=AC,∴CD=AC.
又由(1)可知四边形ACDE是平行四边形,
∴四边形ACDE是菱形.
感悟新知
知1-练
如图 1-1-2,在菱形 ABCD 中, E, F 分别是 BC, CD上的点,且∠ B= ∠ EAF=60°,∠ BAE=18° . 求∠ CEF 的度数 .
例2
知1-练
感悟新知
解题秘方:紧扣菱形的性质、三角形外角的性质求解 .
解:如图 1-1-2,连接 AC.
∵ 四边形 ABCD 是菱形,∠ B=60° ,
∴ AB=BC=CD=DA,∠ D= ∠ B=60° .
∴△ ABC 和△ ACD 均为等边三角形 .
∴ AB=AC,∠ B= ∠ ACF= ∠ BAC=60° .
∵∠ EAF=60°,∴∠ BAC= ∠ EAF.
知1-练
感悟新知
∴∠ BAE= ∠ CAF.
∴△ ABE ≌△ ACF ( ASA ) . ∴ AE=AF.
又∵∠ EAF=60°,∴△ EAF 是等边三角形 .
∴∠ AEF=60° .
∵∠ AEC= ∠ B+ ∠ BAE= ∠ AEF+ ∠ CEF,
∴ 60° +18° =60° + ∠ CEF.
∴∠ CEF=18° .
知1-练
感悟新知
2-1.如图, 在菱形ABCD 中, ∠ BAD=80 °, AB 的垂直平分线交对角线 AC 于点 F, E 为垂足, 连接DF,则∠ CDF 的度数为_____ .
60°
知1-练
感悟新知
如图 1-1-3,四边形 ABCD 是菱形,对角线 AC, BD相交于点 O,且 AB=2.
例3
知1-练
感悟新知
解题秘方:紧扣菱形边、对角线的性质,根据菱形的对角线互相垂直,利用勾股定理求线段长是解决问题的关键 .
知1-练
感悟新知
(1)求菱形 ABCD 的周长;
解:∵四边形 ABCD 是菱形,AB=2,
∴菱形 ABCD 的周长为 2× 4= 8.
知1-练
感悟新知
(2)若 AC=2,求 BD 的长 .
解:∵四边形 ABCD 是菱形, AC=2,
∴ AC ⊥ BD, BO= BD, AO= AC= 1.
在 Rt △ AOB 中,∵ AB=2, AO=1,
∴ BO = = = .
∴ BD = 2BO =2 .
知1-练
感悟新知
3-1. [ 中考· 安徽 ] 如图,在菱形 ABCD 中,AB=2, ∠ A=120 °,过菱形 ABCD 的对称中心 O 分别作边 AB, BC的垂线,交各边于点 E,F, G, H, 则 四 边形EFGH 的周长为( )
A.3+ B.2+2
C.2+ D.1+2
A
感悟新知
知1-练
如图 1-1-4,在菱形 ABCD 中,对角线交于点 O,∠ ABC 与∠ BAD 的度数比为 1∶2,菱形 ABCD的周长是 48. 求:
例4
知1-练
感悟新知
解题秘方:紧扣菱形的性质和面积公式求解 .
知1-练
感悟新知
(1)菱形 ABCD 的两条对角线的长度;
解:∵在菱形 ABCD 中,∠ ABC 与∠ BAD 的度数比
为 1 ∶ 2,∴ ∠ ABC=60°,∠ BAD=120°, AC ⊥ BD.
∴ ∠ ABO=30° .
∵ 菱形 ABCD 的周长是 48,∴ AB=BC=DC=AD=12.
∴ AO=6. ∴ BO= = =6 ,
AC=12,∴ BD=12 .
知1-练
感悟新知
(2)菱形 ABCD 的面积 .
解:S 菱形 ABCD= AC· BD
= × 12× 12 =72 .
菱形面积的两种计算方法
1. 一边与这边上的高的乘积;
2. 两条对角线乘积的一半 .
知1-练
感悟新知
4-1.如图,在菱形ABCD 中,对角线 AC和 BD 相交于点 O,E 是 BC 的中点,连接AE. 若∠ ABC=60°,BE=2 cm,求: (1)菱形ABCD的周长;
知1-练
感悟新知
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵E为BC的中点,BE=2 cm,
∴BC=2BE=4 cm.
∴菱形ABCD的周长为4BC=16 cm.
知1-练
感悟新知
(2)菱形ABCD的面积.
感悟新知
知2-讲
知识点
菱形的判定
2
1.判定定理 1 对角线互相垂直的平行四边形是菱形 .
数学表达式: 如图 1-1-5,在 ABCD 中,
∵ AC ⊥ BD,∴ ABCD 是菱形 .
感悟新知
知2-讲
2. 判定定理 2 四边相等的四边形是菱形 .
数学表达式: 如图 1-1-5,在四边形 ABCD 中,
∵ AB=BC=CD=DA,∴四边形 ABCD 是菱形 .
知2-讲
感悟新知
特别提醒
●菱形的判定定理和性质定理是互逆定理.
●判定菱形的常见思路:
四边形
平行四边形
知2-练
感悟新知
如图 1-1-6,在平行四边形 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 作直线 EF ⊥ BD,分别交 AD, BC 于点 E 和点 F, 连接 BE, DF. 求证: 四 边形BEDF 是菱形 .
例5
知2-练
感悟新知
解题秘方:紧扣对角线垂直这一条件,从判定平行四边形入手判定菱形 .
证明: ∵四边形 ABCD 是平行四边形,
∴ OB=OD, AD ∥ BC.
∴∠ EDO= ∠ FBO,∠ OED= ∠ OFB.
∴△ OED ≌△ OFB(AAS) . ∴ DE=BF.
又∵ DE ∥ BF,∴四边形 BEDF 是平行四边形 .
又∵ EF ⊥ BD,∴四边形 BEDF 是菱形 .
知2-练
感悟新知
5-1.如图, 在三角形纸片 ABC 中, AD 是△ ABC 的角平分线,把△ ABC 进行折叠,使点A 与点 D 重合,折痕与AB 相交于点 E,与 AC相交于点 F. 求证:四边形 AEDF 是菱形 .
知2-练
感悟新知
证明:设AD与EF相交于点O.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵点A与点D关于直线EF对称,
∴EF⊥AD,∴∠AOE=∠AOF=90°.
又∵AO=AO,∴△AEO≌△AFO(ASA).
∴EO=FO.
知2-练
感悟新知
又∵点A与点D重合,∴AO=DO.
∴EF,AD互相平分.
∴四边形AEDF是平行四边形.
又∵AD⊥EF,∴四边形AEDF是菱形.
感悟新知
知2-练
如图 1-1-7,在四边形 ABCD 中, AD=BC,点 E, F, G,H 分别是 AB, CD, AC, BD 的中点,求证:四边形 EGFH 是菱形 .
例6
知2-练
感悟新知
解题秘方:紧扣题中中点条件与线段相等这一特征,从证四条边相等入手判定菱形 .
证明: ∵点 E, H 分别是 AB, BD 的中点,
∴ EH 为△ ABD 的中位线 . ∴ EH= AD.
同理可得 GF= AD, EG= BC, HF= BC.
∵ AD=BC,∴ EH =GF= EG = HF .
∴四边形 EGFH 是菱形 .
知2-练
感悟新知
6-1.四边形的四边长顺次为 a, b, c, d,且 a2+b2+c2+d2=ab+bc+cd+ad, 则此四边形一定是( )
A. 平行四边形 B. 长方形
C. 菱形 D. 正方形
C
菱形的性质与判定
边的关系
边的性质
对角线的性质
对角线的关系
菱形
定义
轴对称性
性质
判定
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
