2022-2023学年 人教版数学九年级下册第二十七章相似微专题 相似与圆综合证明题练习(无答案)
文档属性
| 名称 | 2022-2023学年 人教版数学九年级下册第二十七章相似微专题 相似与圆综合证明题练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 08:42:06 | ||
图片预览



文档简介
人教版数学九年级下册
第二十七章相似微专题——相似与圆综合证明题练习3
1. 如图,在中,,以的中点为圆心、为半径的圆交于点,是的中点,连接,.
判断与的位置关系,并说明理由;
求证:;
若::,,求的长.
如图,延长弦、弦,交于圆外一点,连接、.
证明:∽;
若,,,求.
3.已知,是的直径,是的弦,的割线垂直于于点,交于点,.
求证:是的切线;
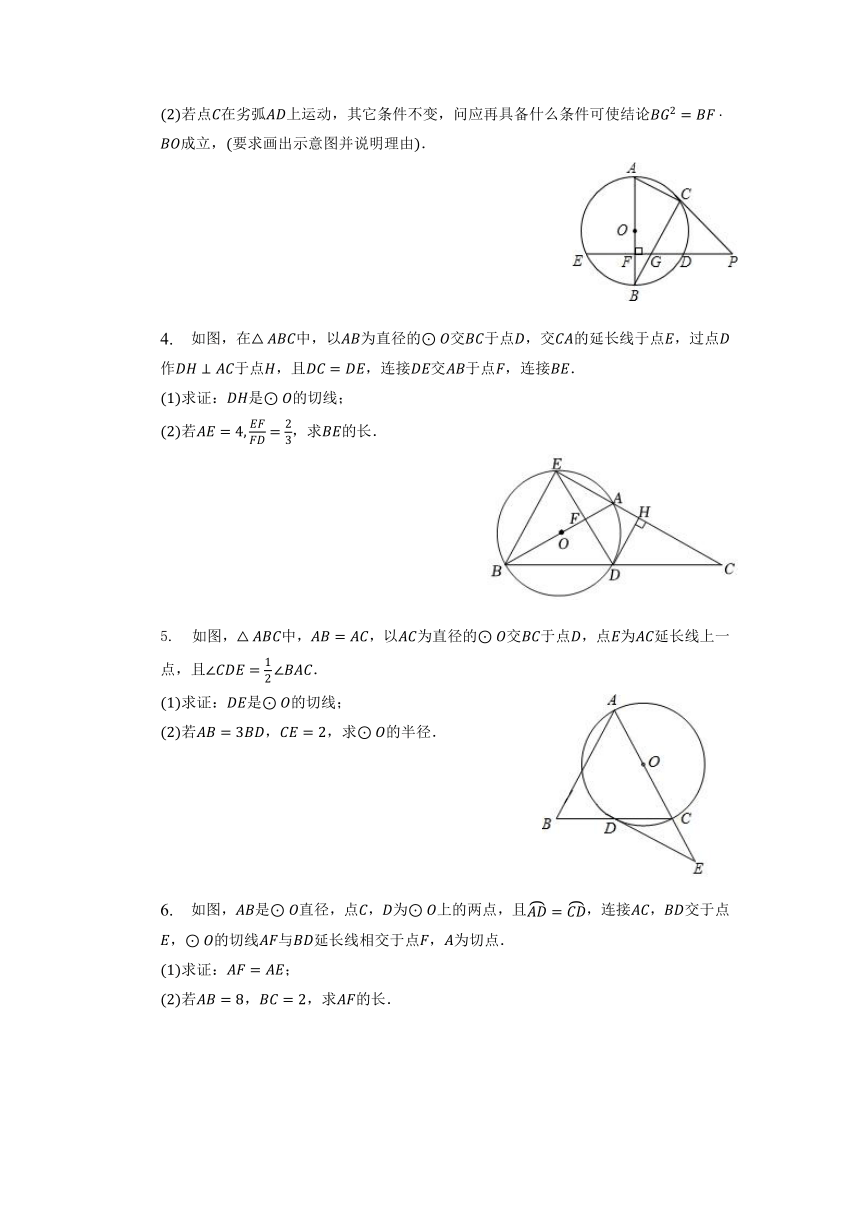
若点在劣弧上运动,其它条件不变,问应再具备什么条件可使结论成立,要求画出示意图并说明理由.
4. 如图,在中,以为直径的交于点,交的延长线于点,过点作于点,且,连接交于点,连接.
求证:是的切线;
若,求的长.
如图,中,,以为直径的交于点,点为延长线上一点,且.
求证:是的切线;
若,,求的半径.
6. 如图,是直径,点,为上的两点,且,连接,交于点,的切线与延长线相交于点,为切点.
求证:;
若,,求的长.
7. 如图,点在以为直径的上,点是的中点,连接并延长交于点,作,交的延长线于点.
求证:是的切线;
若,,求的半径.
如图,是的直径,与交于点,点是半径上一点点不与点,重合连接交于点,连接,若,.
求证:是的切线;
若,,则的长是______.
9. 如图,在中,,点,落在上,的延长线交于点,作直径交于点,切于点,交的延长线于点.
求证:四边形为平行四边形.
若,,求的长.
10. 如图,在中,,以为直径的与边交于点,点是边的中点.
求证:;
求证:是的切线.
11. 如图,在中,为直角,以上一点为圆心,长为半径的圆与相切于点,分别交、于点、.
若,,求的半径;
连接、、、若四边形是平行四边形,试判断四边形的形状,并说明理由.
12. 如图,是的直径,是弦,的平分线交于点,交的延长线于点.
求证:是的切线;
若,,求的半径.
13. 如图,是直径,点在上,平分,是的切线,与相交于点,与相交于点,连接.
求证:;
若,,求的长.
14. 如图,是的直径,为的弦,,与的延长线交于点,点在线段上,且.
求证:与相切
若,,求线段的长.
15.已知为的直径,为的切线,切点为,分别过,两点作的垂线,垂足分别为,,的延长线与延长线相交于点.
求证:∽;
若,,求半径.
16. 如图,中的弦、相交于点.
求证:;
若,,,求线段的长.
17. 如图,在中,,是的角平分线,点在上,以点为圆心,长为半径的圆经过点,交于点,交于点.
求证:是的切线;
若,,求半径的长.
18. 如图,为圆上的一点,为劣弧的中点切于点,交的直径的延长线于点延长线段和线段,使之交于点.
求证:和都是等腰三角形;
若,,求的长.
第二十七章相似微专题——相似与圆综合证明题练习3
1. 如图,在中,,以的中点为圆心、为半径的圆交于点,是的中点,连接,.
判断与的位置关系,并说明理由;
求证:;
若::,,求的长.
如图,延长弦、弦,交于圆外一点,连接、.
证明:∽;
若,,,求.
3.已知,是的直径,是的弦,的割线垂直于于点,交于点,.
求证:是的切线;
若点在劣弧上运动,其它条件不变,问应再具备什么条件可使结论成立,要求画出示意图并说明理由.
4. 如图,在中,以为直径的交于点,交的延长线于点,过点作于点,且,连接交于点,连接.
求证:是的切线;
若,求的长.
如图,中,,以为直径的交于点,点为延长线上一点,且.
求证:是的切线;
若,,求的半径.
6. 如图,是直径,点,为上的两点,且,连接,交于点,的切线与延长线相交于点,为切点.
求证:;
若,,求的长.
7. 如图,点在以为直径的上,点是的中点,连接并延长交于点,作,交的延长线于点.
求证:是的切线;
若,,求的半径.
如图,是的直径,与交于点,点是半径上一点点不与点,重合连接交于点,连接,若,.
求证:是的切线;
若,,则的长是______.
9. 如图,在中,,点,落在上,的延长线交于点,作直径交于点,切于点,交的延长线于点.
求证:四边形为平行四边形.
若,,求的长.
10. 如图,在中,,以为直径的与边交于点,点是边的中点.
求证:;
求证:是的切线.
11. 如图,在中,为直角,以上一点为圆心,长为半径的圆与相切于点,分别交、于点、.
若,,求的半径;
连接、、、若四边形是平行四边形,试判断四边形的形状,并说明理由.
12. 如图,是的直径,是弦,的平分线交于点,交的延长线于点.
求证:是的切线;
若,,求的半径.
13. 如图,是直径,点在上,平分,是的切线,与相交于点,与相交于点,连接.
求证:;
若,,求的长.
14. 如图,是的直径,为的弦,,与的延长线交于点,点在线段上,且.
求证:与相切
若,,求线段的长.
15.已知为的直径,为的切线,切点为,分别过,两点作的垂线,垂足分别为,,的延长线与延长线相交于点.
求证:∽;
若,,求半径.
16. 如图,中的弦、相交于点.
求证:;
若,,,求线段的长.
17. 如图,在中,,是的角平分线,点在上,以点为圆心,长为半径的圆经过点,交于点,交于点.
求证:是的切线;
若,,求半径的长.
18. 如图,为圆上的一点,为劣弧的中点切于点,交的直径的延长线于点延长线段和线段,使之交于点.
求证:和都是等腰三角形;
若,,求的长.
