2.2.2 二次函数y=ax2+c的图象与性质 教案 北师版数学九年级下册
文档属性
| 名称 | 2.2.2 二次函数y=ax2+c的图象与性质 教案 北师版数学九年级下册 |

|
|
| 格式 | doc | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 11:04:23 | ||
图片预览

文档简介
第2课时 二次函数y=ax2+c的图象与性质
【知识与技能】
1.使学生能利用描点法正确作出函数y=x2+2与y=x2-2的图象.
2.理解二次函数y=ax2+c的性质及它与函数y=ax2的关系.
【过程与方法】
让学生经历二次函数y=ax2+c性质探究及性质应用的过程.
【情感态度】
培养学生动手操作的能力及归纳总结与灵活应用知识的能力.
【教学重点】
理解二次函数y=ax2+c的性质及它与函数y=ax2 的关系
【教学难点】
理解二次函数y=ax2+c的性质及它与函数y=ax2的关系
一、情景导入,初步认知
1.二次函数y=x2的图象是 ,它的开口向 ,顶点坐标是 ;对称轴是 ,在对称轴的左侧y随x的增大而 ,在对称轴的右侧y随工的增大而 ,函数y=x2在x= 时,取最值, 其最 值是 .
2.二次函数y=x2十2的图象与二次函数y=x2的图象开口方向、对称轴和顶点坐标是否相同?
【教学说明】巩固旧知,引出新知识.
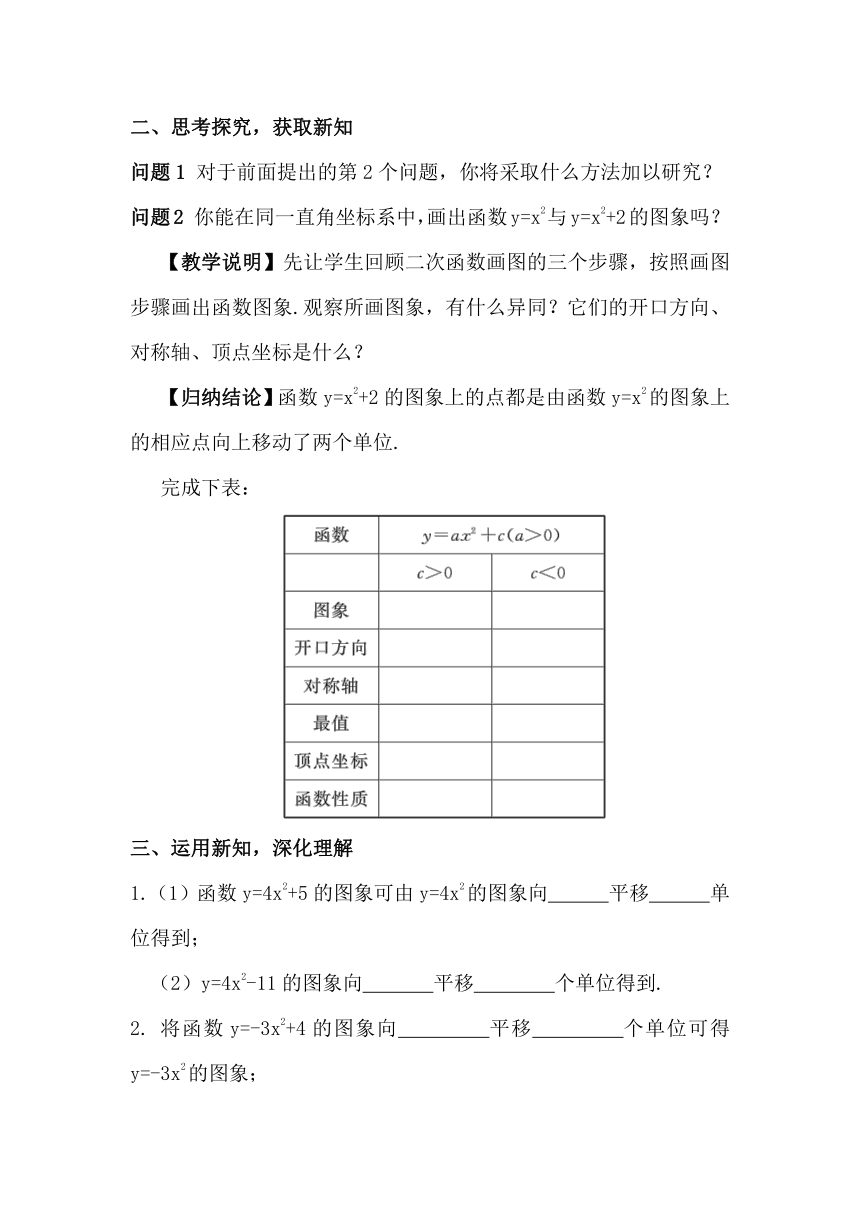
二、思考探究,获取新知
问题1 对于前面提出的第2个问题,你将采取什么方法加以研究?
问题2 你能在同一直角坐标系中,画出函数y=x2与y=x2+2的图象吗?
【教学说明】先让学生回顾二次函数画图的三个步骤,按照画图步骤画出函数图象.观察所画图象,有什么异同?它们的开口方向、对称轴、顶点坐标是什么?
【归纳结论】函数y=x2+2的图象上的点都是由函数y=x2的图象上的相应点向上移动了两个单位.
完成下表:
三、运用新知,深化理解
1.(1)函数y=4x2+5的图象可由y=4x2的图象向 平移 单位得到;
(2)y=4x2-11的图象向 平移 个单位得到.
2. 将函数y=-3x2+4的图象向 平移 个单位可得y=-3x2的图象;
将y=2x2-7的图象向 平移 个单位得到可y=2x2的图象;
将y=x2-7的图象向 平移 个单位可得到y=x2+2的图象.
3.拋物线y=-3x2+5的开口向 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧y随x的增大而 ,当x= 时,取得最 值,这个值等于 .
4. 拋物线y=7x2-3的开口向 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,当x = 时,取得最 值,这个值等于 .
5. 拋物线y =ax2+c与y=3x2的形状相同,且其顶点坐标是(0,1),则其表达式为 .
解:1.(1)上 5 (2)下 11
2.下 4 上 7 上 9
3.下 y轴 (0,5) 增大 减小 0 大 5
4.上 y轴 (0,-3) 减小 增大 0 小 -3
5.y=3x2+1
【教学说明】以上5题,是对本节课的知识点的复习巩固,让学生自主完成,教师做强调.
四.师生互动,课堂小结
本节课你有何收获?本节课你有何疑问
1.布置作业:教材“习题2.3”中第1、2题.
2.完成练习册中本课时的练习.
函数的教学,尤其二次函数是学生普遍感觉较为抽象难懂的知识.在教学过程中,除了让学生多动手画图象,加深学生对函数图象的了解,加深他们对函数性质的了解外,更重要的是让学生参与到函数图象和性质的探索中去.要利用一切可以利用的材料来帮助学生理解所学的知识.本节中通过表格上函数值的变化让学生猜想函数图象的位置变化,给学生留下较深刻的印象,普遍能较好的掌握图象的平移规律.
【知识与技能】
1.使学生能利用描点法正确作出函数y=x2+2与y=x2-2的图象.
2.理解二次函数y=ax2+c的性质及它与函数y=ax2的关系.
【过程与方法】
让学生经历二次函数y=ax2+c性质探究及性质应用的过程.
【情感态度】
培养学生动手操作的能力及归纳总结与灵活应用知识的能力.
【教学重点】
理解二次函数y=ax2+c的性质及它与函数y=ax2 的关系
【教学难点】
理解二次函数y=ax2+c的性质及它与函数y=ax2的关系
一、情景导入,初步认知
1.二次函数y=x2的图象是 ,它的开口向 ,顶点坐标是 ;对称轴是 ,在对称轴的左侧y随x的增大而 ,在对称轴的右侧y随工的增大而 ,函数y=x2在x= 时,取最值, 其最 值是 .
2.二次函数y=x2十2的图象与二次函数y=x2的图象开口方向、对称轴和顶点坐标是否相同?
【教学说明】巩固旧知,引出新知识.
二、思考探究,获取新知
问题1 对于前面提出的第2个问题,你将采取什么方法加以研究?
问题2 你能在同一直角坐标系中,画出函数y=x2与y=x2+2的图象吗?
【教学说明】先让学生回顾二次函数画图的三个步骤,按照画图步骤画出函数图象.观察所画图象,有什么异同?它们的开口方向、对称轴、顶点坐标是什么?
【归纳结论】函数y=x2+2的图象上的点都是由函数y=x2的图象上的相应点向上移动了两个单位.
完成下表:
三、运用新知,深化理解
1.(1)函数y=4x2+5的图象可由y=4x2的图象向 平移 单位得到;
(2)y=4x2-11的图象向 平移 个单位得到.
2. 将函数y=-3x2+4的图象向 平移 个单位可得y=-3x2的图象;
将y=2x2-7的图象向 平移 个单位得到可y=2x2的图象;
将y=x2-7的图象向 平移 个单位可得到y=x2+2的图象.
3.拋物线y=-3x2+5的开口向 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧y随x的增大而 ,当x= 时,取得最 值,这个值等于 .
4. 拋物线y=7x2-3的开口向 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,当x = 时,取得最 值,这个值等于 .
5. 拋物线y =ax2+c与y=3x2的形状相同,且其顶点坐标是(0,1),则其表达式为 .
解:1.(1)上 5 (2)下 11
2.下 4 上 7 上 9
3.下 y轴 (0,5) 增大 减小 0 大 5
4.上 y轴 (0,-3) 减小 增大 0 小 -3
5.y=3x2+1
【教学说明】以上5题,是对本节课的知识点的复习巩固,让学生自主完成,教师做强调.
四.师生互动,课堂小结
本节课你有何收获?本节课你有何疑问
1.布置作业:教材“习题2.3”中第1、2题.
2.完成练习册中本课时的练习.
函数的教学,尤其二次函数是学生普遍感觉较为抽象难懂的知识.在教学过程中,除了让学生多动手画图象,加深学生对函数图象的了解,加深他们对函数性质的了解外,更重要的是让学生参与到函数图象和性质的探索中去.要利用一切可以利用的材料来帮助学生理解所学的知识.本节中通过表格上函数值的变化让学生猜想函数图象的位置变化,给学生留下较深刻的印象,普遍能较好的掌握图象的平移规律.
