北师版数学九年级下册第三章7 切线长定理 教案
文档属性
| 名称 | 北师版数学九年级下册第三章7 切线长定理 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 00:00:00 | ||
图片预览


文档简介
*7 切线长定理
【知识与技能】
掌握切线长定理及其应用.
【过程与方法】
通过经历探索切线长定理的过程,发展探究意识和体会并实践“实验几何——论证几何”的探究方法
【情感态度】
通过应用内切圆相关知识解题,体会把复杂问题转化为简单问题后易于解决,从而树立解决问题的信心。
【教学重点】
切线长定理及应用.
【教学难点】
切线长定理及应用.
一、情景导入,初步认知
1.已知△ABC,作三个内角平分线,说说它具有什么性质?
2.直线和圆有什么位置关系?切线的判定定理和性质定理,它们如何?
【教学说明】由旧知识引入新知识,过渡自然,符合学生的认知规律.
二、思考探究,获取新知
探究:如图,纸上有一⊙O,PA为⊙O的一条切线,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?说明图中的PA和PB有什么关系?
证明:如图,PA、PB是⊙O的两条切线,∴OA丄AP,OB丄BP.
又OA=OB,OP=OP,
∴Rt△AOPRt△BOP
∴PA=PB
因此,我们得到切线长定理.
【归纳结论】经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.过圆外一点所画的圆的两条切线长相等.
【教学说明】发展学生探究知识的意识和“实验几何——论证几何”探究方法.
三、运用新知,深化理解
1.见教材P95例题.
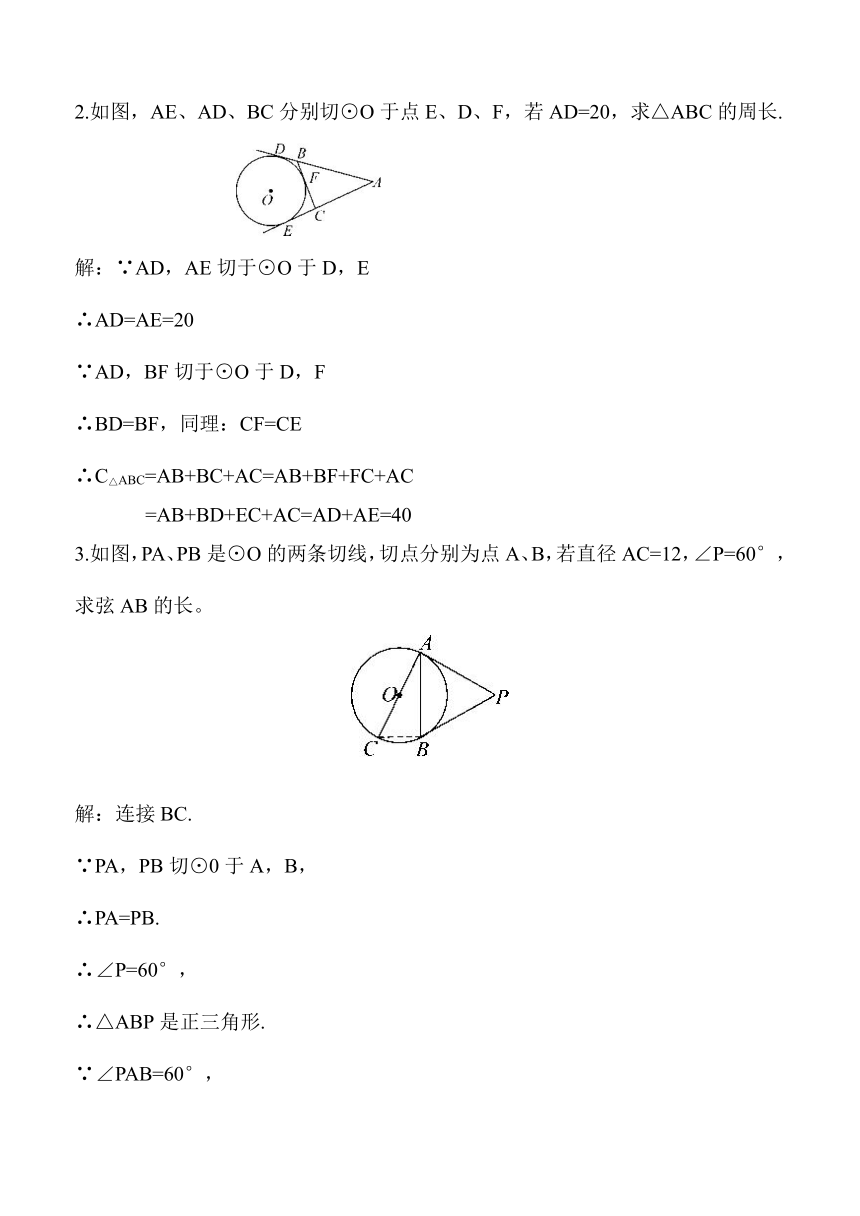
2.如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
解:∵AD,AE切于⊙O于D,E
∴AD=AE=20
∵AD,BF切于⊙O于D,F
∴BD=BF,同理:CF=CE
∴C△ABC=AB+BC+AC=AB+BF+FC+AC
=AB+BD+EC+AC=AD+AE=40
3.如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=12,∠P=60°,求弦AB的长。
解:连接BC.
∵PA,PB切⊙0于A,B,
∴PA=PB.
∴∠P=60°,
∴△ABP是正三角形.
∵∠PAB=60°,
∴PA是⊙O切线,
∴CA⊥AP,
∴∠CAP=90°
∴∠CAB=30°
∵直径AC,
∴∠ABC=90°,
∴cos30°=,
∴AB=6
4.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
解:(1)连接OD,∴OD丄AC
△ODA是直角三角形.
设半径为r,
∴AO = r+2,
∴(r+2)2-r2=16,
解之得,r=3,∴BE=6(cm).
(2)∵∠ABC=90°
∴OB丄BC,
∴BC是⊙O的切线.
∵CD切⊙O于D,
∴CB=CD,令CB=x,
∴AC=x+4,BC=x,AB=8.
∵x2+82=(x+4)2,∴x=6,
S△ABC=×8×6=24(cm2).
【教学说明】通过习题巩固课堂教学成果,思考题使学生保持继续探究的欲望加深对知识的深入思考。
四、师生互动,课堂小结
通过本节课的学习你学会了哪些知识,会了哪些方法?还有哪些疑惑吗?
1. 布置作业:教材“习题3.9”中第1、2、3题.
2.完成练习册中本课时的练习.
本节课是了切线的性质和判定的基础之上,继续对切线的性质的研究,是在垂径定理之后对圆的对称性又一次的认识.体现了图形的认识、图形的变换、图形的证明的有机结合.在习题和内切圆的计算中体现了把复杂问题转化为简单问题后解决问题,从而滲透转化思想和方程思想,提高应用意识.
【知识与技能】
掌握切线长定理及其应用.
【过程与方法】
通过经历探索切线长定理的过程,发展探究意识和体会并实践“实验几何——论证几何”的探究方法
【情感态度】
通过应用内切圆相关知识解题,体会把复杂问题转化为简单问题后易于解决,从而树立解决问题的信心。
【教学重点】
切线长定理及应用.
【教学难点】
切线长定理及应用.
一、情景导入,初步认知
1.已知△ABC,作三个内角平分线,说说它具有什么性质?
2.直线和圆有什么位置关系?切线的判定定理和性质定理,它们如何?
【教学说明】由旧知识引入新知识,过渡自然,符合学生的认知规律.
二、思考探究,获取新知
探究:如图,纸上有一⊙O,PA为⊙O的一条切线,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?说明图中的PA和PB有什么关系?
证明:如图,PA、PB是⊙O的两条切线,∴OA丄AP,OB丄BP.
又OA=OB,OP=OP,
∴Rt△AOPRt△BOP
∴PA=PB
因此,我们得到切线长定理.
【归纳结论】经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.过圆外一点所画的圆的两条切线长相等.
【教学说明】发展学生探究知识的意识和“实验几何——论证几何”探究方法.
三、运用新知,深化理解
1.见教材P95例题.
2.如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
解:∵AD,AE切于⊙O于D,E
∴AD=AE=20
∵AD,BF切于⊙O于D,F
∴BD=BF,同理:CF=CE
∴C△ABC=AB+BC+AC=AB+BF+FC+AC
=AB+BD+EC+AC=AD+AE=40
3.如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=12,∠P=60°,求弦AB的长。
解:连接BC.
∵PA,PB切⊙0于A,B,
∴PA=PB.
∴∠P=60°,
∴△ABP是正三角形.
∵∠PAB=60°,
∴PA是⊙O切线,
∴CA⊥AP,
∴∠CAP=90°
∴∠CAB=30°
∵直径AC,
∴∠ABC=90°,
∴cos30°=,
∴AB=6
4.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
解:(1)连接OD,∴OD丄AC
△ODA是直角三角形.
设半径为r,
∴AO = r+2,
∴(r+2)2-r2=16,
解之得,r=3,∴BE=6(cm).
(2)∵∠ABC=90°
∴OB丄BC,
∴BC是⊙O的切线.
∵CD切⊙O于D,
∴CB=CD,令CB=x,
∴AC=x+4,BC=x,AB=8.
∵x2+82=(x+4)2,∴x=6,
S△ABC=×8×6=24(cm2).
【教学说明】通过习题巩固课堂教学成果,思考题使学生保持继续探究的欲望加深对知识的深入思考。
四、师生互动,课堂小结
通过本节课的学习你学会了哪些知识,会了哪些方法?还有哪些疑惑吗?
1. 布置作业:教材“习题3.9”中第1、2、3题.
2.完成练习册中本课时的练习.
本节课是了切线的性质和判定的基础之上,继续对切线的性质的研究,是在垂径定理之后对圆的对称性又一次的认识.体现了图形的认识、图形的变换、图形的证明的有机结合.在习题和内切圆的计算中体现了把复杂问题转化为简单问题后解决问题,从而滲透转化思想和方程思想,提高应用意识.
