2022-2023学年人教版八年级数学下册19.2一次函数 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册19.2一次函数 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 14:38:23 | ||
图片预览


文档简介
19.2一次函数同点练习
选择题
关于一次函数y=kx+1的表述正确的是()
若函数图象经过第一、二、四象限,k的值可能是3
无论k为何值,图象一定经过(0,1)
图象与x轴的交点坐标(0,1)
若两点A(),B()在该函数图象上,且
正比例函数y=(k-2)x的图象经过一、三象限,那么k的取值范围是()
k>0 B.k>2 C.k<0 D.k<2
已知正比例函数y=kx的图象经过点(-2,4),如果A(1,a)和B(-1,b)在该函数的图象上,那么a和b的大小关系是()
a B.a>b C.a D.a在同一平面直角坐标系中,函数y=kx与y=的图象大致是()
若点A(),B(),C()在一次函数y=-2x+m(m是常数)的图象上,则的大小关系是()
B. C. D.
一次函数y=-2x+m的图象经过第一、二、四象限,则m可能的取值为()
-1 B. C.0 D.1
下列各点中,在一次函数y=-2x+1的图象上的是()
(-1,1) B.(0,1) C.(2,2) D.(-2,3)
设k<2,关于x的一次函数y=(k-2)x+2,当1时,y的最小值是()
A.2k-2 B.k-1 C.k D.k+1
一棵树现在的高度为2.5m,且未来10年内会每年长高22cm,设x年后树的高度为ym,则y与x的函数关系式()
y=2.5+22x B.y=2.5+0.22x C.y=25+22x D.y=2.5x+22
同一平面直角坐标系中,一次函数与的图象如图所示,则关于x的方程的解为()
x=0 B.x=-1 C.x=-2 D.以上都不对
填空题
已知点(-6,m),(8,n)都在直线y=-x-b上,则m____n。(填大小关系)
正比例函数y=kx的图象经过点(-2,6),则k=______.
将直线y=-2x-1向左平移a(a>0)个单位长度后,经过点(1,-5),则a的值为________.
直线y=-x+2和直线y=x-2的交点P的坐标是________.
一次函数y=-2x+6的图象与x轴的交点坐标是__________.
如图,已知,直线y=kx与直线y=ax+4交于点A(2,1),则不等式ax+4>kx的解集为________.
正比例函数y=(k-3)x的图象经过二、四象限,那么k的取值范围是________.
等腰三角形的周长是40cm,腰长y(cm)是底边长x(cm)的函数,此函数的表达式和自变量取值范围为________.
在平面直角坐标系中,将直线y=x+2沿着y轴向下平移3个单位长度,平移后的直线所对应的函数解析式为_________.
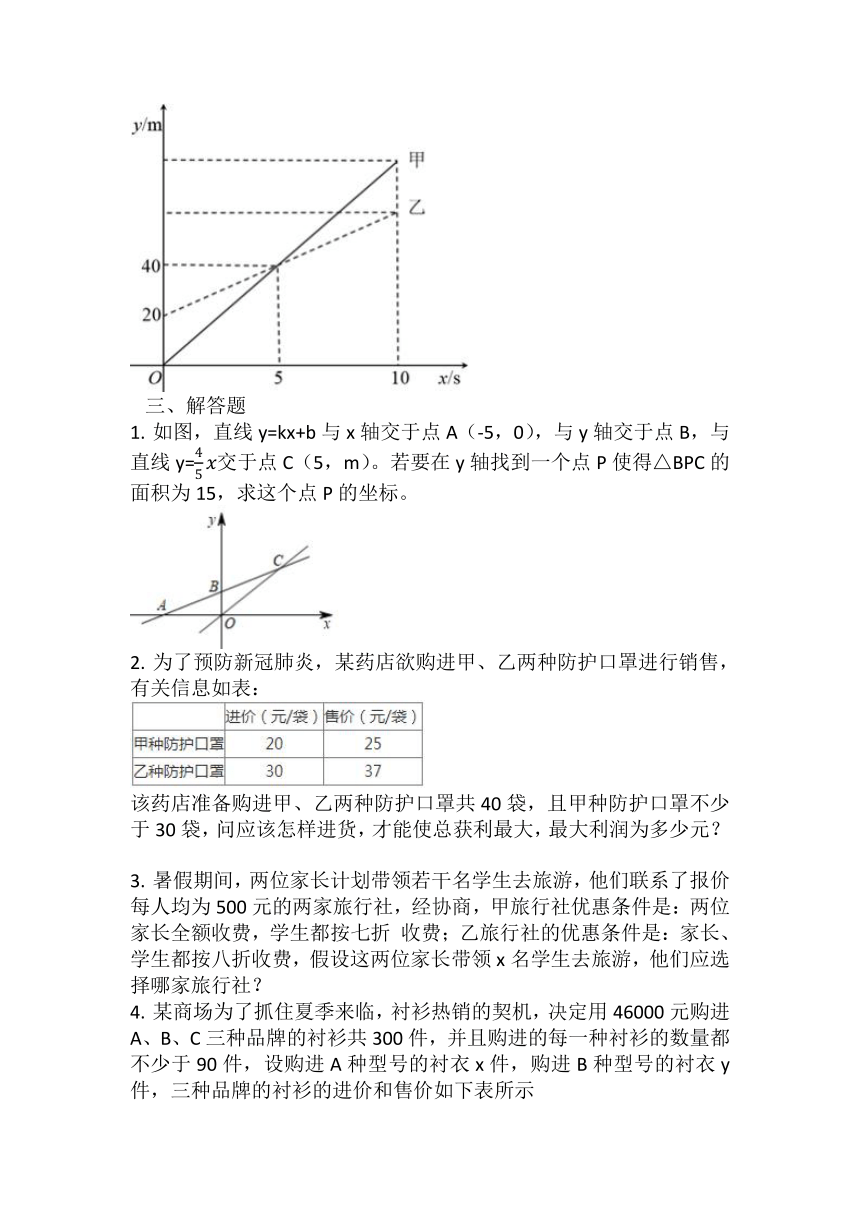
甲无人机从地面起飞,乙无人机距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s,甲、乙两架无人机所在的位置离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,甲无人机的飞行速度为_______m/s;______时甲、乙两架无人机相距10m.
解答题
如图,直线y=kx+b与x轴交于点A(-5,0),与y轴交于点B,与直线y=交于点C(5,m)。若要在y轴找到一个点P使得△BPC的面积为15,求这个点P的坐标。
为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价每人均为500元的两家旅行社,经协商,甲旅行社优惠条件是:两位家长全额收费,学生都按七折 收费;乙旅行社的优惠条件是:家长、学生都按八折收费,假设这两位家长带领x名学生去旅游,他们应选择哪家旅行社?
某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进A、B、C三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件,设购进A种型号的衬衣x件,购进B种型号的衬衣y件,三种品牌的衬衫的进价和售价如下表所示
直接用含x、y的代数式表示购进C种型号衬衣的件数,其结果可表示为_____________________;
求y与x之间的函数关系;
如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润P(元)与x(件)之间的函数关系式;
②求商场能够获得的最大利润。
参考答案
选择题
B 2.B 3.D 4.B 5.B 6.B 7.B 8.A 9.B 10.B
填空题
> 2.-12 3.1 4.(2,0) 5.(3,0) 6.x<2 7.k<3 8. 9.y=x-1 10.8,2.5s或7.5s
三、解答题
1.如图,直线y=kx+b与x轴交于点A(-5,0),与y轴交于点B,与直线y=交于点C(5,m)。若要在y轴找到一个点P使得△BPC的面积为15,求这个点P的坐标。
解:由直线y=交于点C(5,m),可得m=4
C(5,4)
又直线y=kx+b与x轴交于点A(-5,0)
所以:
解得
即y=
设P(0,y)
由题意得
解得 y=8或y=-4
故P(0,8)或(0,-4)
2.为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
解:设利润为w,甲种口罩进货x袋,则乙种为(40-x)袋
由题意得
W=(25-20)x+(37-30)(40-x)
=-2x+280
因为x≥30, k=-2<0
W随x的增大反而减小
所以,当x=30时,w有最大值,为220元
3.暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价每人均为500元的两家旅行社,经协商,甲旅行社优惠条件是:两位家长全额收费,学生都按七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费,假设这两位家长带领x名学生去旅游,他们应选择哪家旅行社?
解:甲旅行社:
乙旅行社:
由=
解得:x=4
因此,当x<4时,选择乙旅行社;当x=4时,选哪家都一样费用 相同;当x>4时,选择甲旅行社。
4.某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进A、B、C三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件,设购进A种型号的衬衣x件,购进B种型号的衬衣y件,三种品牌的衬衫的进价和售价如下表所示
(1)直接用含x、y的代数式表示购进C种型号衬衣的件数,其结果可表示为____300-(x+y)_________________;
(2)求y与x之间的函数关系;
(3)如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润P(元)与x(件)之间的函数关系式;
②求商场能够获得的最大利润。
解:(1)由三种品牌的衬衫共300件,购进A种型号的衬衣x件,购进B种型号的衬衣y件。
所以 购进C种型号衬衣的件数:300-(x+y)
由题意,得
整理,得y=x+20
根据题意,得
p=(200-100)x+(350-200)y+(300-150)(300-x-y)-1000
整理得:p=-50x+44000
由购进的每一种衬衫的数量都不少于90件,得
解得
在p=-50x+44000中,k=-50,p随着x的增大反而减小
所以,当x=90时,P有最大值,为39500元
选择题
关于一次函数y=kx+1的表述正确的是()
若函数图象经过第一、二、四象限,k的值可能是3
无论k为何值,图象一定经过(0,1)
图象与x轴的交点坐标(0,1)
若两点A(),B()在该函数图象上,且
正比例函数y=(k-2)x的图象经过一、三象限,那么k的取值范围是()
k>0 B.k>2 C.k<0 D.k<2
已知正比例函数y=kx的图象经过点(-2,4),如果A(1,a)和B(-1,b)在该函数的图象上,那么a和b的大小关系是()
a B.a>b C.a D.a
若点A(),B(),C()在一次函数y=-2x+m(m是常数)的图象上,则的大小关系是()
B. C. D.
一次函数y=-2x+m的图象经过第一、二、四象限,则m可能的取值为()
-1 B. C.0 D.1
下列各点中,在一次函数y=-2x+1的图象上的是()
(-1,1) B.(0,1) C.(2,2) D.(-2,3)
设k<2,关于x的一次函数y=(k-2)x+2,当1时,y的最小值是()
A.2k-2 B.k-1 C.k D.k+1
一棵树现在的高度为2.5m,且未来10年内会每年长高22cm,设x年后树的高度为ym,则y与x的函数关系式()
y=2.5+22x B.y=2.5+0.22x C.y=25+22x D.y=2.5x+22
同一平面直角坐标系中,一次函数与的图象如图所示,则关于x的方程的解为()
x=0 B.x=-1 C.x=-2 D.以上都不对
填空题
已知点(-6,m),(8,n)都在直线y=-x-b上,则m____n。(填大小关系)
正比例函数y=kx的图象经过点(-2,6),则k=______.
将直线y=-2x-1向左平移a(a>0)个单位长度后,经过点(1,-5),则a的值为________.
直线y=-x+2和直线y=x-2的交点P的坐标是________.
一次函数y=-2x+6的图象与x轴的交点坐标是__________.
如图,已知,直线y=kx与直线y=ax+4交于点A(2,1),则不等式ax+4>kx的解集为________.
正比例函数y=(k-3)x的图象经过二、四象限,那么k的取值范围是________.
等腰三角形的周长是40cm,腰长y(cm)是底边长x(cm)的函数,此函数的表达式和自变量取值范围为________.
在平面直角坐标系中,将直线y=x+2沿着y轴向下平移3个单位长度,平移后的直线所对应的函数解析式为_________.
甲无人机从地面起飞,乙无人机距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s,甲、乙两架无人机所在的位置离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,甲无人机的飞行速度为_______m/s;______时甲、乙两架无人机相距10m.
解答题
如图,直线y=kx+b与x轴交于点A(-5,0),与y轴交于点B,与直线y=交于点C(5,m)。若要在y轴找到一个点P使得△BPC的面积为15,求这个点P的坐标。
为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价每人均为500元的两家旅行社,经协商,甲旅行社优惠条件是:两位家长全额收费,学生都按七折 收费;乙旅行社的优惠条件是:家长、学生都按八折收费,假设这两位家长带领x名学生去旅游,他们应选择哪家旅行社?
某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进A、B、C三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件,设购进A种型号的衬衣x件,购进B种型号的衬衣y件,三种品牌的衬衫的进价和售价如下表所示
直接用含x、y的代数式表示购进C种型号衬衣的件数,其结果可表示为_____________________;
求y与x之间的函数关系;
如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润P(元)与x(件)之间的函数关系式;
②求商场能够获得的最大利润。
参考答案
选择题
B 2.B 3.D 4.B 5.B 6.B 7.B 8.A 9.B 10.B
填空题
> 2.-12 3.1 4.(2,0) 5.(3,0) 6.x<2 7.k<3 8. 9.y=x-1 10.8,2.5s或7.5s
三、解答题
1.如图,直线y=kx+b与x轴交于点A(-5,0),与y轴交于点B,与直线y=交于点C(5,m)。若要在y轴找到一个点P使得△BPC的面积为15,求这个点P的坐标。
解:由直线y=交于点C(5,m),可得m=4
C(5,4)
又直线y=kx+b与x轴交于点A(-5,0)
所以:
解得
即y=
设P(0,y)
由题意得
解得 y=8或y=-4
故P(0,8)或(0,-4)
2.为了预防新冠肺炎,某药店欲购进甲、乙两种防护口罩进行销售,有关信息如表:
该药店准备购进甲、乙两种防护口罩共40袋,且甲种防护口罩不少于30袋,问应该怎样进货,才能使总获利最大,最大利润为多少元?
解:设利润为w,甲种口罩进货x袋,则乙种为(40-x)袋
由题意得
W=(25-20)x+(37-30)(40-x)
=-2x+280
因为x≥30, k=-2<0
W随x的增大反而减小
所以,当x=30时,w有最大值,为220元
3.暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价每人均为500元的两家旅行社,经协商,甲旅行社优惠条件是:两位家长全额收费,学生都按七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费,假设这两位家长带领x名学生去旅游,他们应选择哪家旅行社?
解:甲旅行社:
乙旅行社:
由=
解得:x=4
因此,当x<4时,选择乙旅行社;当x=4时,选哪家都一样费用 相同;当x>4时,选择甲旅行社。
4.某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进A、B、C三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件,设购进A种型号的衬衣x件,购进B种型号的衬衣y件,三种品牌的衬衫的进价和售价如下表所示
(1)直接用含x、y的代数式表示购进C种型号衬衣的件数,其结果可表示为____300-(x+y)_________________;
(2)求y与x之间的函数关系;
(3)如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润P(元)与x(件)之间的函数关系式;
②求商场能够获得的最大利润。
解:(1)由三种品牌的衬衫共300件,购进A种型号的衬衣x件,购进B种型号的衬衣y件。
所以 购进C种型号衬衣的件数:300-(x+y)
由题意,得
整理,得y=x+20
根据题意,得
p=(200-100)x+(350-200)y+(300-150)(300-x-y)-1000
整理得:p=-50x+44000
由购进的每一种衬衫的数量都不少于90件,得
解得
在p=-50x+44000中,k=-50,p随着x的增大反而减小
所以,当x=90时,P有最大值,为39500元
